基于Copula函数的韩-榕-练三江径流丰枯遭遇分析
2021-06-11吴宇彤钟平安万新宇
吴宇彤,钟平安,万新宇,王 涵
(河海大学水文水资源学院,江苏 南京 210098)
0 引 言
韩江、榕江和练江属于粤东沿海诸河,由北向南依次分布(见图1),各流域面积分别为30 112、4 628 km2和1 353 km2,均独流入海。三江流域人均水资源分布不均,人均水资源量分别为2 750、1 138 m3/人和365 m3/人,水资源开发利用率分别为20.3%、22.4%和52%。三江水系连通工程是优化韩江、榕江、练江等水资源配置的战略性工程。三江来水的丰枯互补程度是决定工程效益的重要因素,丰枯遭遇分析是三江水系连通工程可行性研究的重要任务。
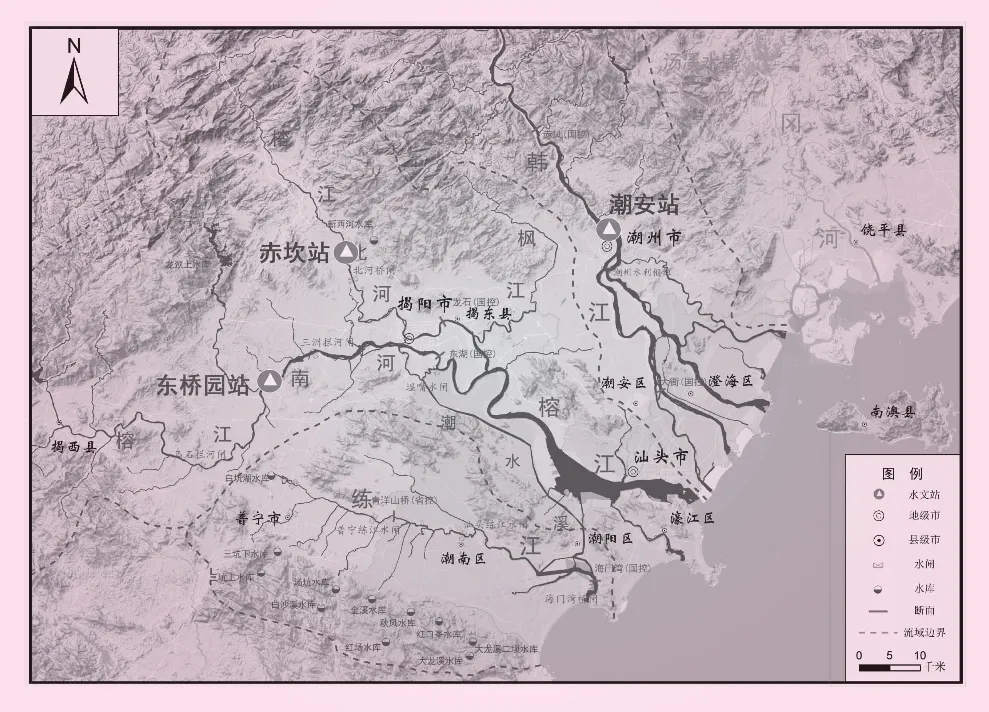
图1 韩江-榕江-练江位置分布
径流(或洪水)遭遇分析方法很多,郑笑天等[1]利用频率分析法分析水文序列的丰枯遭遇,得出王快和西大洋两水库的丰枯遭遇组合频率;薛树文等[2]基于FGM法建立了黄河与小清河年径流量的联合分布函数,得到了二者年径流量丰枯遭遇的概率。在诸多方法中常见的是利用多变量联合概率和条件概率表述遭遇特征[3]。Copula函数又称连接函数,它可通过连接函数表达任意边缘分布的联合分布,并且可以描述变量间的复杂相关结构。为此被广泛应用于暴雨、洪水、干旱等水文时间分析,以及水资源调度、径流丰枯遭遇分析中。尤绮英等[4]采用不同参数估计法拟合了西安供水河流年径流的Copula函数,得到Kendall系数估计法和极大似然估计法均可行的结果;石卫等[5]利用Copula函数构建了南水北调中线水源区与受水区降水的联合分布,对干旱遭遇规律开展了探讨;刘祖发等[6]利用Copula函数构建广东东江流域三大水库入库流量的联合分布,得到三大水库可丰枯互补利用的结论。
本文基于韩江、榕江、练江的降水和径流资料,采用Copula函数分析三江来水丰枯遭遇规律,为三江水系连通工程的建设和运行提供参考。
1 数据和方法
1.1 基础数据
本文收集了韩江流域的潮安站、榕江北河的赤坎站、榕江南河的东桥园站1968年~2010年的逐月径流资料,榕江南河8个和练江6个气象站的同期降水资料。
练江流域缺乏径流资料,榕江南河与练江比邻,下垫面条件接近,本文首先利用榕江南河的降雨与径流资料,建立降雨径流关系[7],再根据练江流域的降雨资料得到练江的径流过程系列。
1.2 方法原理
1.2.1Copula函数及其参数估计
利用Copula函数构建多维联合分布模型,分析多条河流间径流的丰枯遭遇关系是目前认为较好的方法。Copula函数又称连接函数。Copula函数基于Sklar定理[8]:设X、Y为连续的随机变量,边缘分布函数分别为FX和FY,F(x,y)为变量X和Y的联合分布函数[9],如果FX和FY连续,则存在唯一的函数Cθ(u,v)使得
F(x,y)=Cθ(Fθ(x),Fθ(y)),∀x,y
(1)
式中,Cθ(u,v)为Copula函数;θ为待定参数。
Gumbel Copula函数[2]、Clayton Copula函数[9]和Frank Copula函数[10]是水文领域常用的3种Copula 函数,详见表1。

表1 水文领域常用的3种Copula函数
Copula函数的参数估计一般采用Kendall系数估计法或极大似然法,后者包括全参数极大似然估计法、半参数极大似然估计法和逐步极大似然估计法[9-11]。
本文将采用半参数极大似然法,其原理为用边缘分布的经验函数值代替理论函数值,利用τ与θ的关系计算得到θ,不同Copula函数的τ与θ参数均不相同。
τ为描述二维变量间非线性相关系数的Kendall相关系数,即
(2)
(3)
当τ可知时,可由表1中的公式根据τ和θ的关系计算得到θ。
1.2.2边缘分布优选
本文采用GAMMA分布、LOGISTIC分布、对数正态分布(Log-Normal Distribution)对韩江、榕江、练江的包括年、汛期、非汛期的3个时间尺度,共9组径流变量进行拟合,利用稳健性较好、计算误差较小的线性矩法[12](MME法)进行参数估计。
通过K-S方法检验边缘分布、Copula函数拟合结果,并用均方根误差法(RMSE)和AIC信息准则法计算评价指标,根据AIC值大小选取最优的边缘分布。计算公式如下
(4)
(5)
式中,pei和pi分别为经验频率和理论频率;N为径流序列的样品大小;M为时变边缘分布和Copula模型的评估参数个数。
1.2.3丰枯遭遇分析
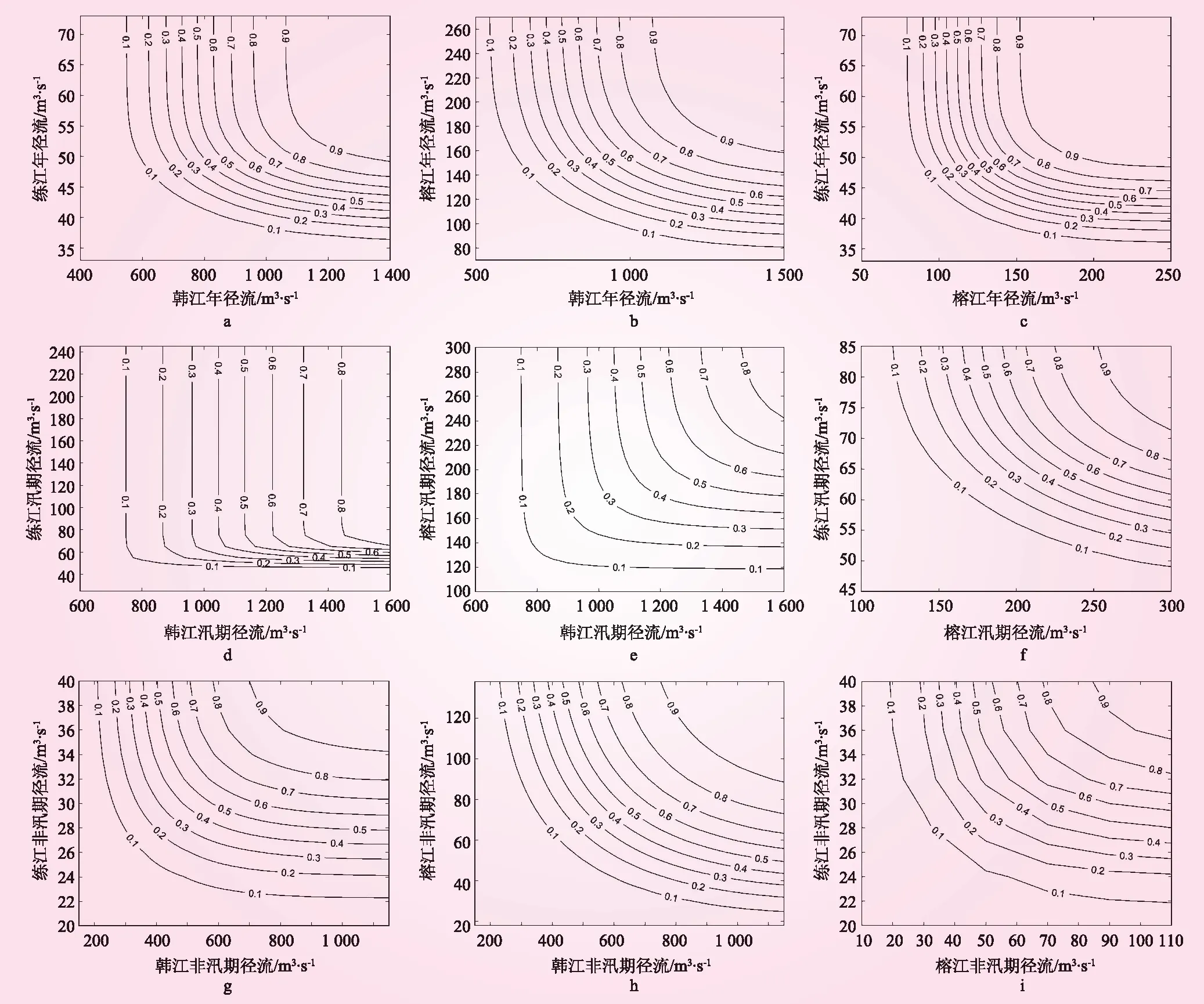
单一河流的径流丰枯划分呈现的是径流的概率区间。水文中的径流丰枯等级划分,一般基于距平百分率或者频率[13-14]。本文将年径流丰枯等级划分为丰水、平水、枯水3级,设枯水、平水的分界值流量为Xpk,平水、丰水的分界值流量为Xpf。若流量Xi 丰枯遭遇是指多条河流的径流在不同概率区间的组合事件[15-17]。多条河流流量的丰枯遭遇本质是联合概率问题。 设2组数据分别为X和Y,Xpk、Xpf、Ypk、Ypf分别为X和Y枯平、平丰的分界值,其对应的边缘分布结果为upk、upf、vpk和vpf,则这两组数据相应不同丰枯组合概率的计算公式如下: (1)X丰Y丰,P(X≥Xpf,Y≥Ypf)=1-upf-vpf-C(upf,vpf); (2)X丰Y枯,P(X≥Xpf,Y (3)X平Y丰,P(Xpk≤X (4)X平Y枯,P(Xpk≤X (5)X平Y平,P(Xpk≤X (6)X枯Y枯,P(X C(u,v)指u和v的Copula函数,各丰枯组合的计算公式可类推。 选用GAMMA、Logistic和对数正态分布对韩江、榕江、练江的年、汛期、非汛期的共9组径流变量进行拟合,采用MME法拟合参数,并利用K-S方法进行检验评价,适线结果的RMSE值和AIC值、K-S检验的P值和D值如表2、3所示。选取原则为AIC值越小越好,计算得到的P值均通过0.05的显著性水平,D值的临界值为DC=0.204。9组数据的边缘分布函数均选取GAMMA分布函数。以练江年径流为例,其频率分布及年径流关系见图2、图3。 表2 边缘分布适线结果 图2 练江年径流频率分布 图3 练江实际与理论年径流关系 不同尺度数据的GAMMA分布函数参数见表4。 表3 K-S检验 表4 GAMMA分布参数 构建Clayton Copula,Frank Copula和Gumbel Copula 3种二元Copula联合分布模型,用半参数极大似然法估计Copula函数的参数,9组数据的参数估计结果和评价结果见表5。从韩江、榕江和练江年、汛期和非汛期3个时期的径流量两两Copula联合分布的拟合评价的结果来看,不同组合的不同函数的RMSE和AIC值均不同;选择评价指标较小的Copula函数类型,可以得到较高的模型的拟合精度。表5中带下划线的数值即对应其所取的Copula函数。由表5可知,有7个组合均Gumbel Copula函数评价指标占优,只有汛期的韩江-练江和韩江-榕江组合Clayton Copula函数略优。考虑到水文领域相关研究中Gumbel Copula函数应用最为广泛,所以本文也采用Gumbel Copula函数。 表5 不同Copula函数参数估计及评价结果 以年径流频率37.5%和62.5%将径流划分为丰水、平水、枯水3级,根据年、汛期、非汛期的韩江、榕江、练江流量的同一时间尺度两两间的Copula函数,可以计算得出相应的二维联合分布,得到不同丰枯遭遇组合情景的概率,即不同联合分布在特定边际分布下的联合概率(见表6)。各时期不同组合径流丰枯遭遇的联合分布等值线图见图4。从图4中可以查出水源区与受水区径流遭遇发生各种径流组合的频率。例如,由图4韩江-练江非汛期径流遭遇等值线图可以查出当水源区韩江非汛期径流为500 m3/s时,练江出现非汛期径流为24 m3/s的概率为0.109 6。从而可以定量得出韩江、榕江、练江之间发生各种径流组合遭遇的概率,其丰枯遭遇表现出以下特征。 图4 三江流域径流丰枯遭遇的联合分布等值线 表6 三江丰枯遭遇频率 (1)从空间看,榕江-练江的丰枯同步的概率大于韩江-榕江、韩江-练江,榕江-练江的年尺度同步概率为0.465 4,大于韩江-榕江、韩江-练江的0.444 2、0.415 8,榕江-练江的汛期尺度同步概率为0.547 4,大于韩江-榕江、韩江-练江的0.458 2、0.496 6。练江和榕江的同步性较好是因为练江和榕江主要水量来源的榕江南河地理距离较为接近,下垫面条件和气候条件相似。而韩江与练江距离较远,且本次研究的韩江潮安站位于韩江下游,与榕江、练江的下游较为接近,而韩江的主要水量来自上游,流域面积较大,故来水量较大时,距离较近的榕江-练江的同步概率较大。 (2)分析韩江、榕江、练江的丰枯遭遇,得到“丰-平”、“丰-枯”、“平-丰”等利于调水的组合概率,讨论水量较大的水源区韩江、榕江对受水区练江补水有利的丰枯组合。从时间看,对于年时间尺度:①练江作为受水区,与韩江、榕江的丰枯互补概率较大,存在韩江、榕江作为水源对练江进行补水的可能性;②韩江作为第一水源,对榕江和练江利于调水的概率分别为0.466 1、0.470 1,榕江作为第二水源及过水通道,练江作为受水区,利于调水的概率为0.511 6。三者间丰枯异步且利于调水的组合概率较大,存在丰枯补偿的特征,具备三江联合调水的可能性。韩江来水较丰的情况下,韩江可在满足自身下游河道内外需水的前提下,通过过水通道榕江为练江调水,同时可利用余水供给榕江,榕江也可在来水较丰的情况下,补偿练江,韩江、榕江两水源具有相机补水的特征。 (3)对于调水的主要时段非汛期而言,韩江-练江、榕江-练江的利于调水概率分别为0.443 3、0.464 1,概率越大,来水充沛的上游越可以补偿来水偏少的下游,越有利于调水,这一情况对持续缺水的受水区练江而言是非常有利的。 本文利用Copula函数构建了广东粤东中小河流域韩江、榕江、练江三江径流的二维联合分布模型,分析其丰枯遭遇,主要结论如下: (1)练江和榕江地理位置相近,下垫面条件和气候条件相似,所以表现出较强的丰枯同步性。韩江潮安站径流主要来自韩江上游,所以韩江与榕江、练江同步性稍差。 (2)三江两两丰枯异步的概率明显大于丰枯同步的概率,韩江与练江的丰枯异步概率大于榕江与练江的概率,但均大于相应的丰枯同步概率。 (3)非汛期韩江-练江、榕江-练江的利于调水概率分别为0.443 3、0.464 1,有利于跨流域补水。2 结果分析与结论
2.1 流量边缘分布的确定
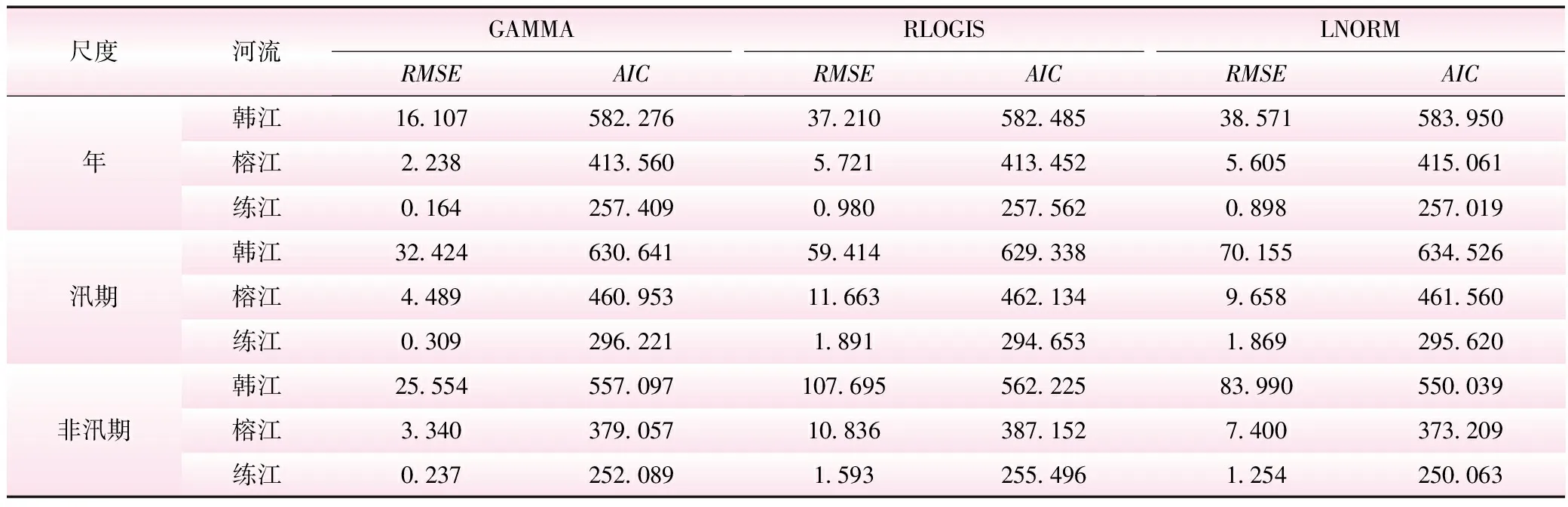
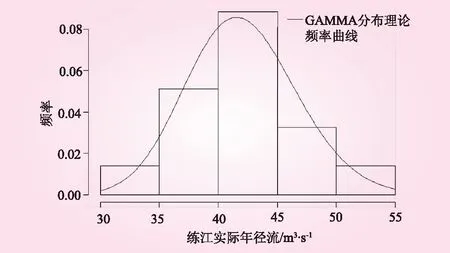


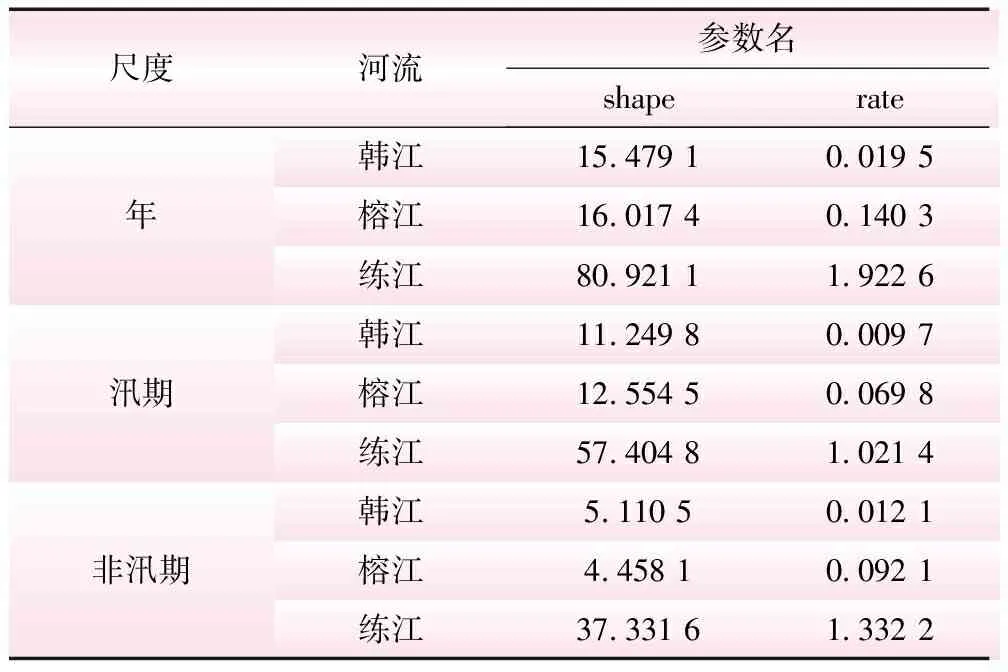
2.2 Copula函数的确定

2.3 三江两两丰枯遭遇分析

3 结 语
