固定式锥形阀水力特性试验研究

王 蛟，胡亚安，严秀俊，傅陆志丹

(1.重庆交通大学重庆西南水运工程科学研究所，重庆 400016；2.重庆交通大学内河航道整治技术交通行业重点实验室，重庆 400016；3.重庆交通大学重庆西科水运工程咨询中心，重庆 400016；4.南京水利科学研究院，江苏 南京 210029)

0 引 言

控制阀门是水力式升船机所特有的核心部件，类似于传统电力驱动式升船机的电机，直接关系到升船机的运行速度与安全。2016年底，世界上第一座水力式升船机——景洪升船机成功试通航，标志着该类升船机的实践成功。但作为最新型的一类升船机，其基础应用理论中还有许多问题值得深入研究和优化[1]。景洪工程建设初期，将精确控制流量作为控制阀门选型的第一要素，最终确定采用德国VAG公司生产的活塞式调流阀(后文简称活塞阀)作为控制阀门[2]。后期原型观测成果表明[3]，活塞阀控流精确，可以满足景洪工程的运行要求，但也存在一些不足，不利于水力式升船机的推广应用。该阀型在小开度下流阻较大，泄流能力偏低，限制了升船机的运行速度；大开度下空化明显，噪声尖锐，振动强烈，不利于阀后管道安全。未来水力式升船机控制阀门的运行水头差更高、提升重量更大，活塞阀的以上特点将被进一步放大。可见，活塞阀将难以满足未来水力式升船机的发展需要，深化研究控制阀门的选型问题十分必要。

作者基于水力式升船机控制阀门选型问题，曾对典型工业阀门的水力特性及研究进展进行了对比综述[4]，发现固定式锥形阀(后文简称锥形阀)也较为适应水力式升船机的运行特性。锥形阀的相关研究主要集中在优化阀体内部结构，达到抑制空化、降低振动等目的。杨和梅等[5]对锥阀的阀口结构与空化的关系进行了研究，数值模拟结果表明，倒角长度的改变对阀口间隙以及阀芯锥面与柱面相接的地方的负压会产生比较大的影响。潘广香等[6]对锥阀内部流场进行仿真分析，对锥阀阀口及阀芯都进行了优化，结果表明，优化后的锥阀可抑制空化，整体性能优于传统结构。孙芃等[7]采用CAE软件ANSYS对锥阀流场进行了数值模拟，优化了阀口设计，结果显示，改进后的结构有利于抑制空化，可减小振动。秦武等[8]利用CFD数值模拟方法对锥形阀大开度下的流场结构进行了研究，在环形孔套后部增加了锥形孔套部件以改善其内部流场情况，降低了最高压力、最大流速，减小了流动死区及涡流区对过流能力的影响。贺杰等[9]利用CFD仿真计算了背压对锥形阀空化特性的影响，研究结果表明，锥形阀阀腔内节流口后部区域，流体流速增高、压力降低，是空化发生的主要区域。可见，经过防空化设计的锥形阀适用于管中调流调压，但对其阀后流态及管壁压力特性等的相关研究较少。为全面掌握固定式锥形阀的水力特性，本文通过物理模型试验对固定式锥形阀进行了全面、深入的研究分析。

1 物理模型设计

本研究中锥形阀通径DN=150 mm，带导流罩。试验在南京水利科学研究院多功能空化空蚀试验厅中进行。该试验厅实现了水泵控制、阀门控制、系统压力、流量监控的自动化。供水系统工作压力最高可达1.5 MPa，最大流量为0.15 m3/s，可为试验阀门提供近乎工程原型的试验条件。根据试验要求，试验模型主要由阀前整流段、试验阀门段、玻璃管道和阀后稳压段组成，模型设计见图1，试验阀门段照片见图2。

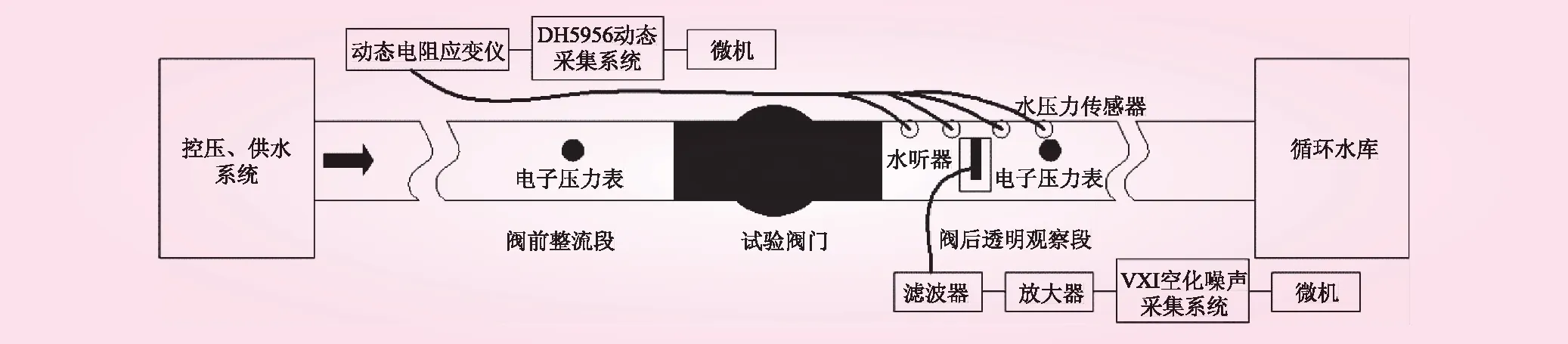
图1 试验模型设计

图2 试验阀门段照片

2 试验成果分析

2.1 阀门流量特性

在通航建筑物输水系统中，阀门流量系数的一般表达式如式1。流量系数是阀门实际过流量与理想过流量的比值。由于存在局部阻力损失与沿程阻力损失，实际过流量总是小于理想过流量。流量系数表示为

(1)

式中，μ为流量系数；A为阀门过流面积；Q为阀门过流流量；ρ为流体密度；P1、P2分别为阀前、阀后参考断面稳定压力。

2.1.1流量系数随开度的变化

锥形阀套筒行程、流量系数随阀门开度的变化规律如图3所示。由图3可知，锥形阀流量系数随开度(n)增大而增加，最大流量系数约为0.678。n=0.1～0.7时，锥形阀流量系数增幅随开度增大基本一致，线性度较好；n=0.8～1.0时，流量系数增幅随开度增大在变缓，在开度为0.8时存在增幅由稳定转减的“拐点”。

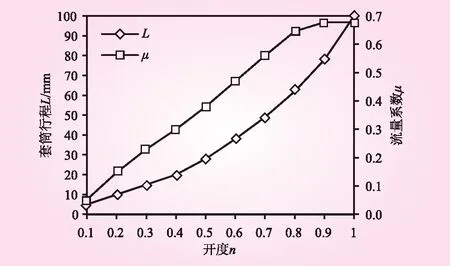
图3 锥形阀各开度下套筒行程、流量系数关系

从阀门结构角度分析，锥形阀泄流能力主要受以下因素影响：

(1)阀门进口面积。阀门进口面积(Ai)的大小决定了阀门的最大过流量。阀门进口面积计算公式为

(2)

式中，Ri为锥形阀进口直径。本文试验锥形阀Ai=17 671 mm2。

(2)套筒过流面积。锥形阀通过控制套筒行程(L)来调节阀门过流能力。套筒过流面积(A)<阀门进口面积(Ai)时，阀门过流能力随套筒过流面积的增大而增加；套筒过流面积(A)>阀门进口面积(Ai)时，阀门过流能力将不再增加。套筒过流面为圆台锥面，其计算公式为

A=πRTL-πrl

(3)

式中，RT为圆台下底面直径；L为圆台下底面母线长度；r为套筒具体行程下圆台上底面直径；l为套筒具体行程下圆台上底面母线长度。

基于公式(2)、(3)可计算锥形阀过流面积随套筒开度的变化规律，结果如表1所示。由表1可知，当开度为0.9时，A>Ai；n=0.8～0.9时，阀门过流面积已达极限，继续增大套筒行程，阀门过流能力不会再提升。因此，n=0.8时，流量系数随开度的变化曲线将出现“拐点”。

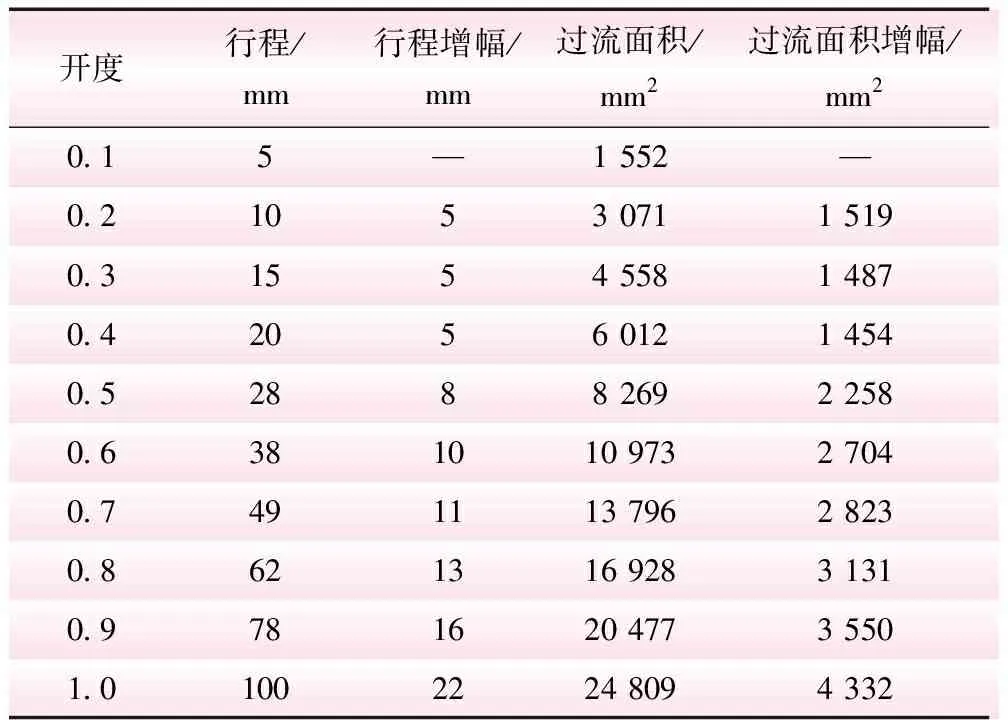
表1 锥形阀各开度套筒行程特性

2.1.2流量系数随背压、压差的变化

典型开度下(n=0.4)，流量系数随压差的变化规律如图4所示。由图4可知，当阀门未发生空化时(流量系数未突增前)，流量系数的变幅较小；阀门空化后，流量系数先突增，后迅速持续减小。具体体现为，同一开度下，固定背压，逐渐增大上游压力，在未发生空化前，流量系数基本维持稳定。在临界空化压差附近，流量系数会小幅突增，后随压差的进一步增大而开始明显下降。对于该现象的一种解释是，在发生可监测到的空化现象前，于空化初生部位表面会形成细微气泡，这些气泡会在结构物表面与过流水体间形成一层水气膜，将水流与结构物表面分离开来，近似于降低了结构物表面的糙率，从而小幅提高了过流能力。随背压的增大，流量系数随压差变化的总体规律类似，但在临界空化状态下，阀门的流量系数峰值略有下降。

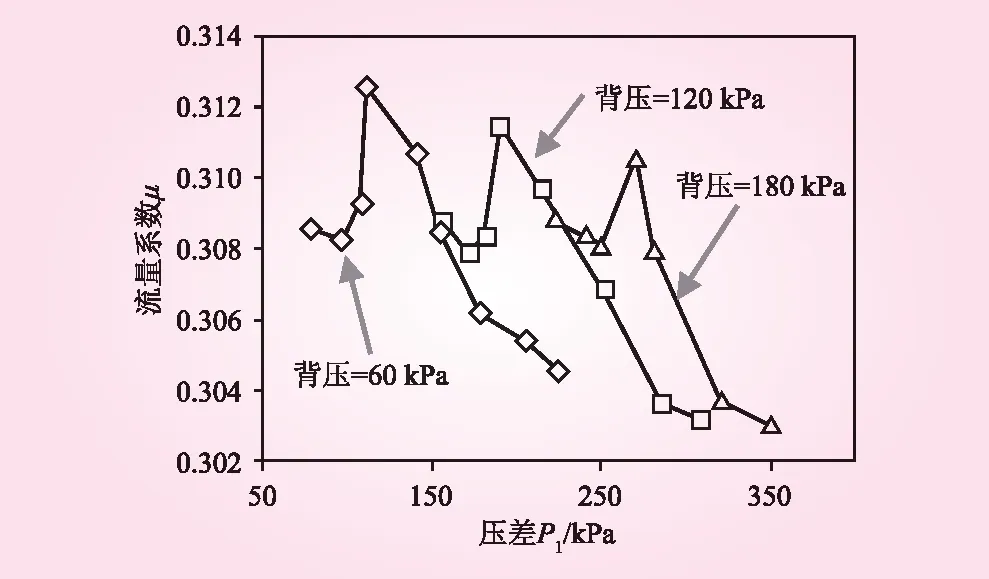
图4 流量系数随压差的变化规律(n=0.4)

2.2 阀门空化特性

2.2.1流场结构及空化现象

典型开度下(n=0.3)，锥形阀后的空化现象如图5所示，该类阀门的空化类型为雾状空化。由图可知，锥形阀出流较为均匀，流场结构简单，近似于等截面稳定出流，雾状空化泡分布均匀、细碎微小。

图5 阀门典型开度空化示意

2.2.2临界空化数随开度、背压的变化

本文空化数定义如式4。以σi表征水流处于临界空化状态，σ>σi时，表明阀门段无空化；σ≤σi时，阀门段存在空化。σi越小，说明阀门空化初生时阀后作用水头越小，即阀门无空化的工作水头差越大，阀门的防空化性能越好。

(4)

式中，σ为空化数；Patm、Psv分别为当地大气压及水的饱和蒸汽压；v为参考断面平均流速。

空化现象对阀门最直接的影响之一就是降低阀门的泄流能力，锥形阀典型开度(开度为0.4时)流量系数与相对空化数的关系如图6所示。σ/σi=1，即是临界空化状态。由图可知，当σ/σi>1时，流量系数基本维持稳定；当σ/σi<1时，流量系数随相对空化数的减小而逐渐下降。当相对空化数为0.5时，活塞阀流量系数降低约10%，锥形阀流量系数降低约5%。

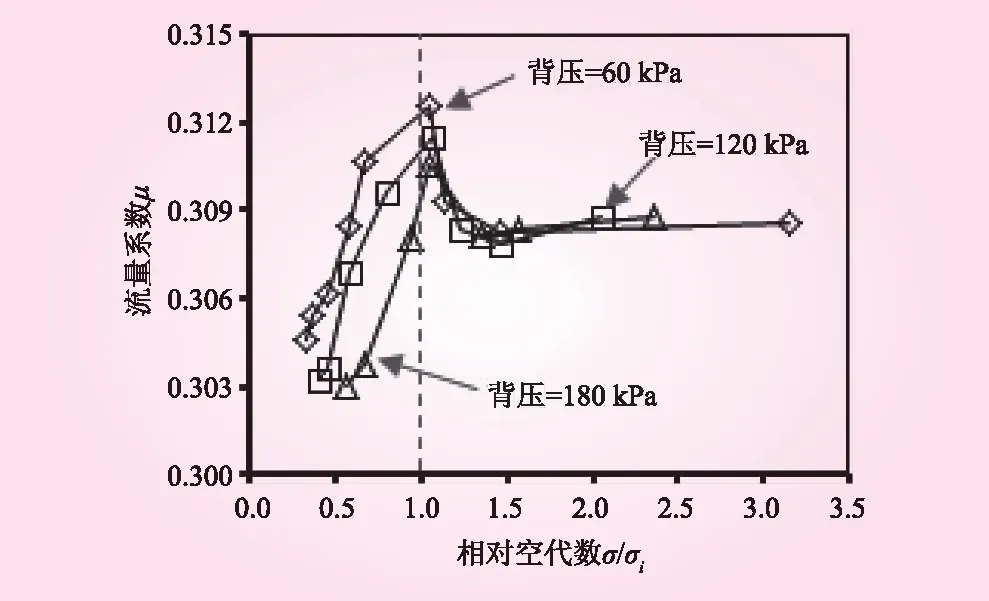
图6 锥形阀流量系数与相对空化数关系(n=0.4)

2.3 阀后管壁压力特性

典型开度下(n=0.3)，锥形阀后管壁沿程压力特性随相对空化数的变化规律如图7所示。由图7可知，锥形阀出流较为均匀，流场结构较简单，阀口附近不存在明显的低压区，阀后沿程时均压力(Pav)较稳定，变幅很小。随相对空化数的减小、压差增大，2倍阀门通径附近时均压力略有增大，水流对管壁的冲击稍有增强。对比压力均方根值(Prms)可知，锥形阀阀口附近压力均方根值最大，但沿水流方向迅速下降，在2倍阀门通径附近即降至稳定值，而后基本保持不变。不同相对空化数下，压力均方根值沿程分布规律不变，仅阀口附近有所增大。

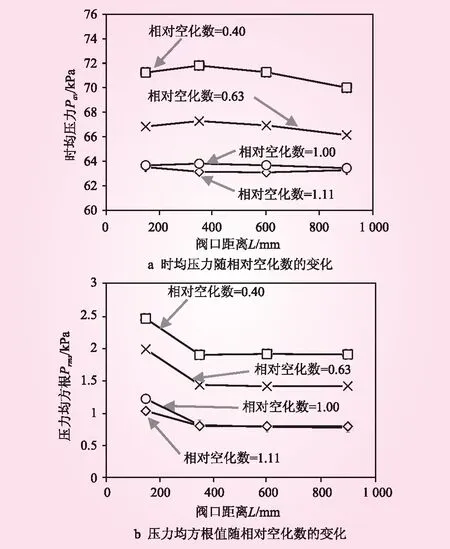
图7 锥形阀典型开度阀后管壁压力特性(n=0.3)

3 结 语

(1)锥形阀直接控制套筒来启闭阀门，流量系数随开度变化的线性度较好，过流能力较强，阀门全开时流量系数达到0.678(带导流罩)。阀门未空化时，流量系数基本保持不变，阀门空化后，流量系数会先小幅突增，再随空化程度的增强而迅速下降。

(2)锥形阀的空化类型为雾状空化。由于导流罩的整流作用，锥形阀出流均匀，空化泡细碎微小。在临界空化压差附近，流量系数会小幅突增，后随压差的进一步增大而开始明显下降。

(3)基于导流罩的整流消能作用，锥形阀近似等截面出流，阀后流态简单稳定，管壁时均压力沿程分布变化较小、压力脉动较弱。

综上所述，锥形阀泄流能力较强，雾状空化较易抑制，阀后流态简单稳定，对管壁的直接冲击较小，较为适合水力式升船机的发展需要，但其抗空化性能略差。在高压差、大流量工况下，阀门空化难以避免，因此必须辅以可靠的阀门防空化技术，才能确保水力式升船机控制阀门及其阀后管道安全。