基于改进GWO和SVM的大坝变形预测
2021-06-11李明军王均星潘江洋
李明军,王均星,潘江洋,刘 昊,李 慧
(1.水能资源利用关键技术湖南省重点实验室,湖南 长沙 410014;2.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014;3.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
1 研究背景
变形是大坝工作性态的综合性反映,而基于原型观测数据建立准确的变形预测模型,对确定大坝运行行为,保证其长期安全运行具有重大意义[1]。传统的变形预测模型(统计模型、确定性性模型和混合模型)难以表达变形量与影响因素(水位、温度和时效)之间的复杂关系[2],而支持向量机在求解样本少、维数高的非线性问题上具有明显的优势。但是,在建立基于SVM的大坝结构特性识别模型时,核参数和惩罚因子的优化选择是一个值得研究的问题。
灰狼优化算法(Grey Wolf Optimizer,GWO)是由Mirjalili等[3]参照灰狼的社会等级和狩猎行为,提出的一种新的元启发式算法。GWO算法模拟了灰狼种群的社会等级和群体狩猎行为,通过对灰狼种群的跟踪、包围、狩猎、攻击等过程来实现智能算法的优化[4]。该优化算法因采用新型的搜索机制,调整参数少且全局搜索能力强,在解决一些优化问题时表现出良好的性能。Zhang等[5]采用GWO算法来解决无人作战飞行器(UCAV)二维路径规划问题,结果表明GWO算法求得最终解的质量、速度和稳定性比其他进化算法都要更加优秀。但与其他元启发式算法类似,GWO算法在解决复杂函数优化问题时容易陷入局部最优,出现早熟收敛等问题。
本文在前人研究的基础上,提出了一种改进灰狼算法优化支持向量机的大坝变形预测模型(MGWO-SVM)。通过差分算法丰富初始种群,引入差分算法的交叉和变异算子,改进灰狼算法的开拓和搜索能力。用改进后的灰狼优化算法对SVM进行参数寻优,并将其应用于大坝变形预测。以锦屏一级特高拱坝为例,将MGWO-SVM模型与SVM、GWO-SVM模型的预测结果进行对比分析。工程实践表明,相较于MGWO-SVM模型与SVM、GWO-SVM模型,MGWO-SVM模型泛化能力更强,预测精度更高。
2 算法
2.1 灰狼优化算法
GWO算法模拟了灰狼种群的社会等级和群体狩猎行为,通过对灰狼种群的跟踪、包围、狩猎、攻击等过程来实现智能算法的优化[4]。灰狼算法对狼群的社会等级的行为进行建模,主要分为四个部分:α,β,δ和ω,如图1所示。
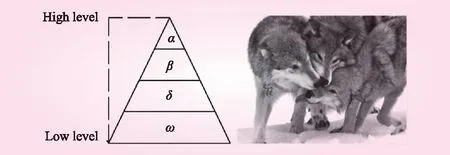
图1 灰狼的社会等级制度
α是最佳的解决方案,其次是β和δ,其余的解决方案属于ω。最接近猎物的前3匹最好的狼是α,β和δ,它们引导ω在有希望的搜索区域中搜索猎物。在狩猎过程中,狼会更新其围绕α,β和δ的位置,即
(1)
(2)
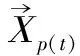
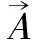
(3)
(4)

在GWO算法中,始终假定α,β和δ接近猎物的位置。在狩猎过程中,保存当前为止的前3个最佳解决方案,然后剩余的狼(如ω)可以根据前3个最佳灰狼的位置来重新定位。灰狼的位置根据以下等式更新。
(5)
(6)
(7)
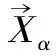
2.2 差分进化算法
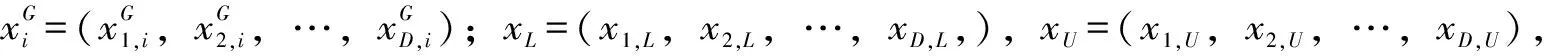
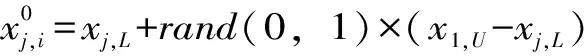

(4)选择。针对具体问题,对所有突变交叉个体进行评估。当前个体的适应度超过前一代则代表突变交叉操作成功,当前个体保留;当前个体适应性比不上前一代,则保留更好的个体。具有最优适应度的个体会成为这一代个体的最优值,当达到最大迭代次数或终止条件时就停止进化,否则持续进行下一轮。
2.3 改进灰狼优化算法
标准灰狼算法随机产生初始种群,有时会由于无法确保种群的多样性而陷入局部最优的困境[3];而差分进化算法是通过群体中个体和个体之间相互合作与竞争来产生群体智能,从而指导优化搜索的方向[6]。基于灰狼优化算法和差分进化算法各自的优缺点,通过差分进化的变异来丰富标准灰狼优化算法初始种群的多样性,利用灰狼算法全局最优的搜索能力来确保组合算法的收敛性,提出更为高效的改进灰狼进化算法(MGWO),已期达到加强全局搜索能力的同时避免陷入局部最优的目的。具体步骤如下:①设置MGWO优化算法的相关参数,例如种群大小N,交叉概率CR,搜索维,最大迭代次数tmax,搜索范围上下界ub和lb,缩放因子F。②初始化参数a、A和C,用进化突变操作以生成中间体(变体种群),然后,差分算法的竞争选择操生成初始化种群个体,并设置迭代时间t=1。③计算单个灰狼个体的目标函数值,根据目标函数值的大小排序,并分别选择最佳的3个个体Xα、Xβ和Xδ。④根据式(5)计算其他灰狼个体与最优Xα、Xβ和Xδ之间的距离,并根据式(6)更新每只灰狼的位置。⑤更新a、A和C的值,然后将交叉操作运用到种群的个体位置,保留更好的成分,然后竞争选择运算以生成新的个体,并计算所有灰狼的目标函数值。⑥更新前3个灰狼个体的Xα、Xβ和Xδ位置。⑦判断是否有最大迭代次数tmax,是则退出该算法并输出全局最优Xα的目标函数值;否则,t=t+1,并转移到第三步以继续执行。
3 大坝变形预测模型
为了获得更好的预测效果,将提出的MGWO应用到SVM,得到基于MGWO-SVM算法的大坝变形预测模型。数据通过SVM输入空间中的高斯核映射到隐层空间,需要确定惩罚系数C和核参数γ,通过MGWO算法演化得到两个参数的最佳值,SVM基于优化之后的参数组合(C,γ)对大坝进行预测。
MGWO-SVM算法的优化过程主要包含两个阶段:第一阶段,通过MGWO算法得到最优参数组合(C,γ);第二阶段,利用上一阶段得到的SVM优化模型进行预测。MGWO-SVM算法进行大坝变形预测的流程示意如图2所示。
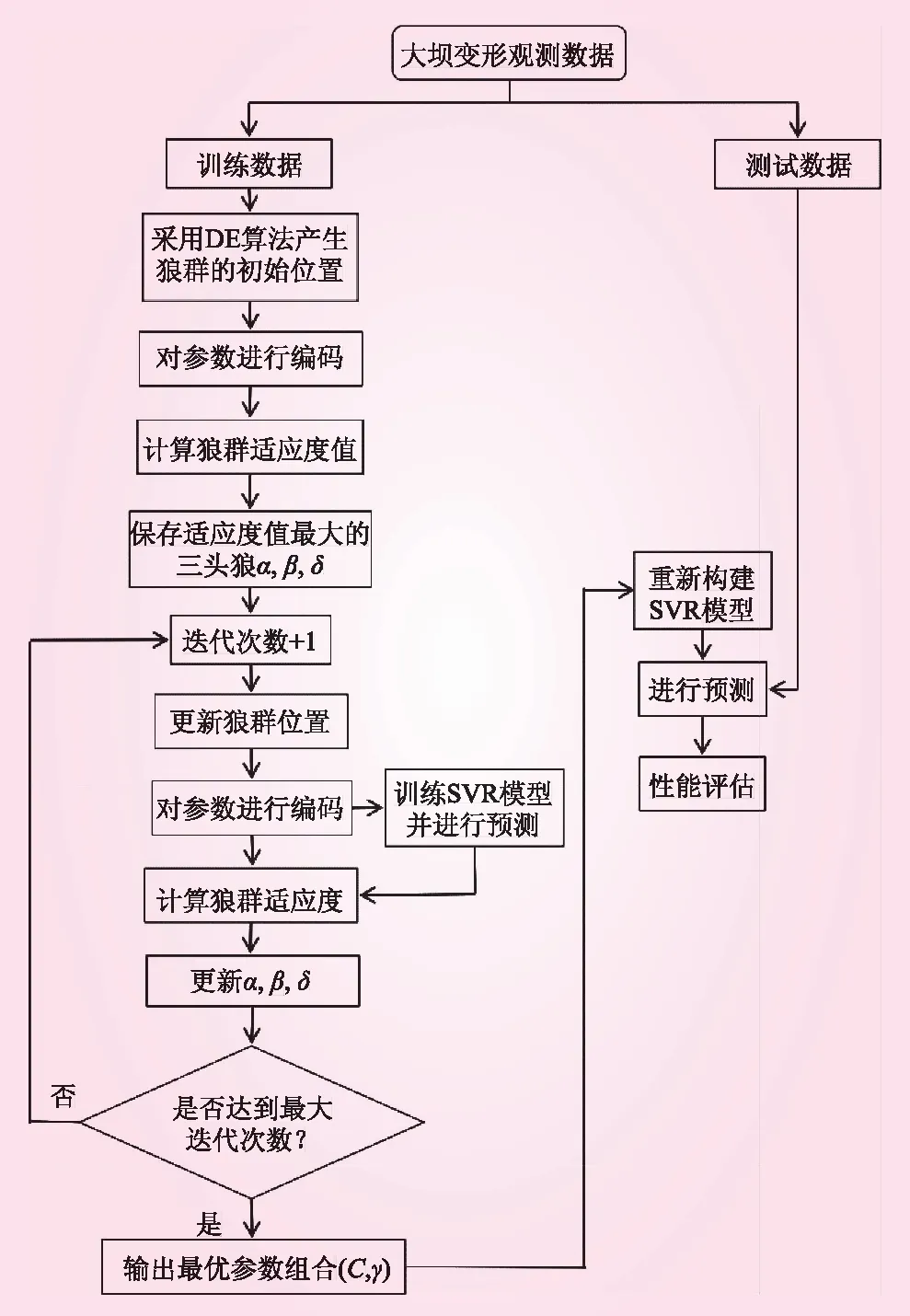
图2 建立基于MGWO-SVM算法的大坝安全监测模型流程
大坝变形预测主要步骤如下:
(1)获取大坝变形数据。
(2)对数据集进行划分,分别获得训练数据集和测试数据集,并对数据集进行归一化处理。
(3)初始化灰狼种群的参数。设置种群规模和最大迭代次数等参数,确定搜索空间的范围,同时对惩罚系数C和核参数γ进行编码,成为狼群中位置的两个维度。
(4)采用DE算法初始化灰狼种群。
(5)初始化a、A和C。采用式(3)、式(4)初始化系数A和C,而收敛因子a=2。
(6)计算灰狼个体的适应度值。通过灰狼的位置确定组合参数(C,γ),并基于此参数组合采用训练数据训练SVM模型,将计算的均方误差MSE确定灰狼个体的适应度值。
(7)保留具有最佳适应度值的三头灰狼,即α狼、β狼和δ狼。
(8)参照α狼、β狼和δ狼的位置,采用式(5)~(7)更新灰狼个体的位置。
(9)计算所有灰狼个体的适应度值。通过灰狼的位置确定组合参数(C,γ),并基于此参数组合采用训练数据训练SVM模型,将计算的均方误差MSE确定灰狼个体的适应度值。
(10)更新α狼、β狼和δ狼的位置和适应度值。
(11)更新a、A和C。采用公式(3)~(4)初始化系数A和C,而收敛因子a此处从a=2开始线性递减直到a=0。
(12)判断是否达到最大迭代次数。若是达到,则输出最佳参数组合(C,γ);若是没有达到,则返回步骤(8),迭代次数加1。
(13)输出最优参数组合(C,γ),并基于训练集对SVM进行重新训练。
(14)通过MGWO-SVM模型对待测样本进行测试,并对模型的预测结果进行性能评价。
为了衡量MGWO-SVR算法的性能,分别采用均方误差(MSE)、平均绝对百分误差(MAPE)和平方相关系数(R2)三个性能指标对预测模型性能进行评估[2]。平方相关系数(R2)越接近1,说明模型预测效果越好;均方误差(MSE)和平均绝对百分误差(MAPE)越小,说明模型预测效果越好。
4 工程实例
锦屏一级混凝土拱坝[7]是目前世界上最高的拱坝,位于四川省凉山市。坝顶高程1 885.0 m,最大坝高305.0 m。其坝顶和坝底最大厚度分别为16.0 m和63.0 m。大坝的水平位移通过垂线测量,如图3所示。
图3 坝体垂线布置
本文以锦屏一级拱坝特高拱坝11号坝段测点PL11-1在2013年9月到2017年2月的径向位移数据为研究对象,2013年9月到2016年1月的位移观测数据为训练集,则剩余时间段数据为预测集。从2013年9月到2017年3月期间,测点的径向位移和水位变化如图4和图5所示,其中,“-”表示向下游的位移,“+”表示向上游的位移。
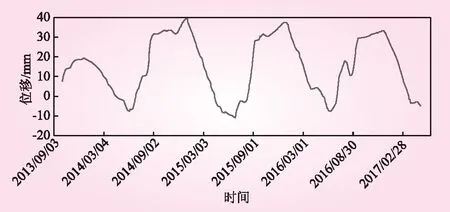
图4 测点位移变化
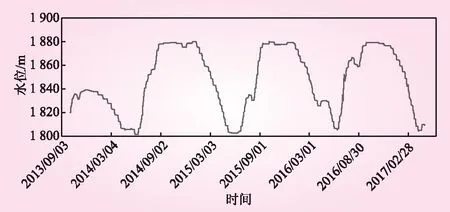
图5 测点水位变化
4.1 建模变量
本文以大坝变形影响因素为模型的输入变量[2],大坝的影响因素主要有水位因子、温度因子以及时效因子。由此,确定基于智能算法的大坝变形预测模型的输入变量为
(8)
式中,H为当前水位;H0为基准时刻上游水位;t为当前监测时间与开始监测时间之间的累计天数;t0为用于构建预测模型的数据序列的开始时间到当前时间之间的累计天数,θ=t/100,θ0=t0/100。
为了匹配模型的一致性且避免大数据信息淹没小数据信息的情形,将所有的源数据归一化在[0,1]范围内[2]。
4.2 参数设置
为了比较改进的灰狼算法(MGWO)和灰狼算法(GWO)的收敛效果,图6给出了适应度值与迭代次数的关系。总体参数设置如下:种群大小为20,最大迭代次数为200。惩罚因子C的取值范围为[0.01,100]、核参数γ的取值范围为[0.01,1 000]。当迭代次数达到200时,计算停止。在以锦屏一级特高拱坝实测数据为例,采用MGWO算法得到的SVM的最优参数[C,γ]为[7.485 6,0.010 0]。
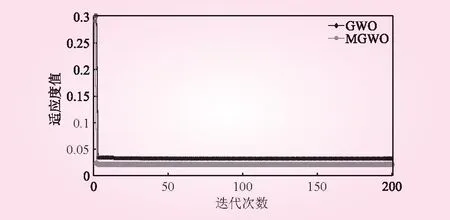
图6 适应度值与迭代次数的关系
从图6中可以看出,MGWO算法减少了迭代次数,能够更快地找到最接近最佳目标的解决方案。主要原因是差分算法增加了初始灰狼种群的多样性,提高了灰狼算法的全局搜索能力,从而加快了收敛速度和收敛精度。
4.3 计算结果
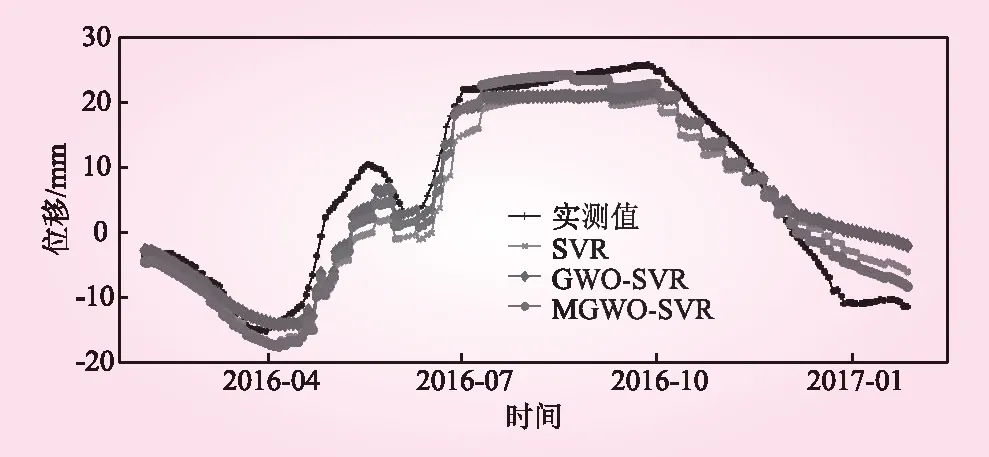
根据4.1节,建立以大坝变形影响因素为输入变量的SVM、GWO-SVM、MGWO-SVM模型。SVM、GWO-SVM和MGWO-SVM模型的预测性能如表1和图7、图8所示。比较表中的3项性能参数可知:平方相关系数(R2)由大到小排序为MGWO-SVM> GWO-SVM> SVM模型;平均绝对百分比误差(MAPE)和均方误差(MSE)从小到大排序为MGWO-SVM 表1 SVM、GWO-SVM和MGWO-SVM模型的预测性能 图7 SVM、GWO-SVM和MGWO-SVM模型的预测效果对比 图8 SVM、GWO-SVM和MGWO-SVM模型的预测误差对比 本文引入差分算法中的交叉和变异算子来丰富标准GWO算法的初始种群,然后结合SVM,提出了基于MGWO-SVM的大坝变形预测模型。通过锦屏一级特高拱坝的实测位移数据,对比分析SVM、GWO-SVM和MGWO-SVM模型的预测性能,主要结论如下: (1)MGWO算法的优化性能比常规GWO算法更加优越。采用差分算法保证种群多样性,可以有效地提高算法寻找高质量解的能力,仿真测试表明,MGWO算法的收敛精度更高。 (2)SVM、GWO-SVM和MGWO-SVM模型均能有效预测大坝变形趋势,但MGWO-SVR模型的预测精度更高,模型更加稳定。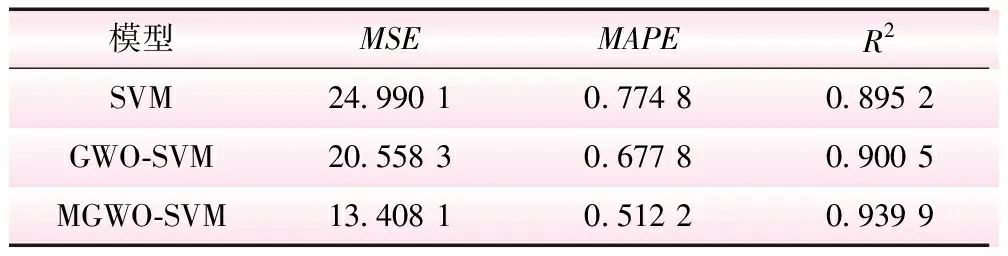

5 结 论
