集成KPCA与t?SNE的滚动轴承故障特征提取方法
2021-06-10王望望邓林峰赵荣珍吴耀春
王望望 邓林峰 赵荣珍 吴耀春

摘要: 针对滚动轴承原始数据集包含高维非敏感特征的问题,提出一种集成核主成分分析(Kernel Principal Component Analysis, KPCA)与t?分布随机邻域嵌入(t?distributed Stochastic Neighbor Embedding, t?SNE)的滚动轴承故障低维敏感特征提取方法。该方法先计算滚动轴承原始振动信号的时域、频域以及时频域特征,构建初始高维特征数据集。利用KPCA降低高维数据集的相关性,在最大化高维数据全局特征方差的目标下,提取出非线性特征子集。通过t?SNE充分挖掘故障特征数据集的局部结构信息,进一步获取具有高判别性的低维敏感特征子集。将低维特征子集输入到k?近邻分类器(k?nearest Neighbor Classifier, KNNC)进行分类,以分类准确率和聚类结果作为度量指标,对特征提取结果的优劣予以评价。上述过程综合考虑了数据集的全局和局部结构特征,充分利用了数据自身的结构信息,从而可准确提取其低维敏感特征。将该方法用于滚动轴承故障诊断实验中,通过与其他典型特征提取方法进行对比,及其对含噪情况下轴承故障特征的准确提取,验证了方法的有效性。
关键词: 故障诊断; 滚动轴承; 故障特征提取; 核主成分分析; t?分布随机邻域嵌入; k?近邻分类器
中圖分类号: TH165+.3; TH133.33 文献标志码: A 文章编号: 1004-4523(2021)02-0431-10
DOI:10.16385/j.cnki.issn.1004-4523.2021.02.024
引 言
滚动轴承故障诊断的本质是模式识别,特征提取则是模式识别的重要组成部分[1]。若要对滚动轴承故障进行精确诊断,就需要提取大量的故障特征,进而可从各个方面反映故障的固有特性[2]。但是,这会造成故障特征维数过高,同时还可能引入非敏感特征,从而影响诊断精度[3]。因此,从高维特征集中提取低维敏感特征,对滚动轴承故障诊断具有十分重要的意义。
数据的结构特征包括描述其整体特性的全局结构特征和数据近邻点分布特性的局部结构特征,前者反映数据的外部形状,后者反映数据的内在属性[4?5]。其中,人工神经网络、主成分分析等均可作为描述全局结构特征的有效方法。核主成分分析(Kernel Principal Component Analysis, KPCA)[6]是在主成分分析基础上改进而来的方法,它通过将核技术引入PCA中,使线性不可分的原始数据在高维特征空间变得线性可分。马萍等[7]将KPCA与核局部保持投影算法相融合,并利用融合的新方法准确提取出滚动轴承4种状态的敏感矢量,实现了轴承不同状态的精确诊断。姜洪权等[8]提出一种适用于高维非线性特征数据的聚类算法,该方法将KPCA与密度聚类相结合,不仅有效获取了原始数据的非线性特征,也解决了传统密度聚类方法对高维数据不适用的问题。但是,KPCA只能提取数据集的全局结构特征信息,即可实现数据集整体方差最大化,而对数据集的局部结构特征信息却无能为力。
流形学习是一类能够从高维数据中提取低维局部特征信息的方法,它可以充分挖掘数据的局部结构特征,是处理非线性数据内部属性的强有力工具[9]。流形学习分为线性和非线性两类,一般情况下高维数据往往都具有非线性结构[3]。典型的非线性流形学习算法包括局部线性嵌入(Locally Linear Embedding, LLE)、等距特征映射(Isometric Mapping, ISOMAP)、拉普拉斯特征映射(Laplacian Eigenmaps, LE)、局部保持投影(Locality Preserving Projection, LPP)等[10?14]。t?分布随机邻域嵌入(t?distributed Stochastic Neighbor Embedding, t?SNE)[15]是一种无监督非线性流形学习算法,能够有效地从高维数据中提取低维敏感特征信息,从而充分挖掘数据的局部结构信息。张康等[16]提出一种基于t?SNE数据驱动模型的盾构装备刀盘健康评估的新方法,利用t?SNE准确地从原始高维特征空间中提取出了低维特征信息,精确地评估了刀盘的性能状态。文献[17]对非线性流形嵌入方法t?SNE在关键字查找任务方面的有效性进行了探讨。文献[18]对t?SNE进行了改进,而改进后的t?SNE利用一个新的高维概率分布来逼近真实的概率分布,将其应用于遥感数据的降维处理,结果表明改进的t?SNE在性能上优于原方法。文献[19]将核技术引入t?SNE以增强其处理非线性数据的能力,实验结果表明,核t?SNE对复杂数据具有更好的泛化能力。但利用t?SNE及其改进方法,都只能提取数据样本的局部结构特征,无法获取数据集的全局结构特征。
基于上述分析,为保证特征提取过程中对故障数据的全局和局部结构特征信息能够进行全面挖掘,本研究提出一种集成KPCA与t?SNE的滚动轴承故障特征提取方法。该方法能够兼顾样本数据的全局和局部结构特征,不仅可实现数据整体方差最大化,同时保持了数据的局部近邻结构。实验结果显示,本文提出的方法能够准确提取出滚动轴承故障特征信息,从而验证了该方法的有效性。
1 基本原理与简介
1.1 核主成分分析算法
2.2 集成KPCA与t?SNE的特征提取方法
KPCA是一种面向全局的特征提取方法,通过非线性映射使低维空间中线性不可分的原始数据在高维空间变得线性可分。这一过程是在最大化高维数据全局特征方差的目标下,提取出原始数据的全局非线性特征。t?SNE是一种非线性流形学习算法,它将高维空间数据点之间的相似性以概率形式来表示,并假设数据点在高维空间服从高斯分布,在低维空间服从t分布。从高维到低维的降维过程,t?SNE能够充分挖掘出嵌入在高维空间中的低维局部流形结构,获取数据的局部结构特征信息。因此,综合二者的各自优势,本研究提出一种集成KPCA与t?SNE的滚动轴承故障特征提取方法。该方法的优势在于:充分考虑了样本数据的全局和局部结构特征,通过融合数据的不同结构特征信息,使得KPCA与t?SNE流形学习算法在特征提取过程中实现优势互补。
2.3 集成KPCA与t?SNE的故障特征提取流程设计
结合滚动轴承故障振动数据特性,设计集成KPCA与t?SNE的滚动轴承故障特征提取方法流程如图1所示。实施步骤如下:
Step1: 采集原始故障振动信号,由故障信号计算得到时域、频域和时频域的多种量化特征,构建原始高维故障特征集X。
Step2: 对构建的原始高维故障特征集X进行归一化处理,得到处理后的故障特征集X1。
Step3: 选择径向基函数作为KPCA的核函数,利用KPCA对X1进行处理,通过特征值的累积贡献率确定主成分特征个数,获得初次降维的故障特征集X2。
Step4: 将X2输入t?SNE进行处理,得到最终提取的故障特征集X3。
Step5: 将X3输入到KNNC中进行分类识别,然后计算低维敏感特征集的类间距离Sb和类内距离Sw的比值Sb/Sw以及KNNC的故障分类准确率,对特征提取方法的性能进行量化评价。
从图1可见,整个轴承故障特征提取过程,首先通过KPCA提取初始特征集的全局结构信息,选择累积贡献率大于95%的前s维主成分特征得到一次降维特征集;然后利用t?SNE继续挖掘故障特征集的局部结构信息,找到蕴含在数据中的低维流形结构,实现低维特征提取。因此,该方法综合了KPCA与t?SNE算法的各自优势,能够充分挖掘出滚动轴承故障特征数据集的全局和局部结构信息,可从原始高维特征数据集中有效提取出低维敏感特征。
3 方法的实验验证
3.1 实验装置简介
为验证集成KPCA与t?SNE的滚动轴承故障特征提取方法的可行性与有效性,利用图2所示的滚动轴承故障模拟实验台及图3所示轴承故障进行实验验证。实验台型号为HZXT?DS?001,主要由三相变频调速电机、底座、加载装置、转轴、传感器、轴承座以及滚动轴承等部件组成。实验中采集NSK6308深沟球轴承在5种不同运行状态下的振动信号,其中4种轴承故障类型分别为内圈故障、外圈故障、保持架故障和滚动体故障,还有正常运行类型。每种类型都采集5个通道的振动信号,其中前3个通道分别测试轴承座两个径向方向和一个轴向方向,其由振动加速度传感器进行测试;后2个通道测试故障轴承所支撑转轴的径向振动,其由非接触式的电涡流传感器进行测试。实验中内圈常规转速为2600 r/min,加速度传感器型号为HD?YD232,电涡流传感器型号为WT?φ8,数据采集卡为HD9200多通道数据采集卡,信号采样频率为8 kHz,每个样本采样长度为2048个数据点。
3.2 特征数据集的构成
由于振动信号的时域、频域以及时频域特征能够从不同角度刻画轴承故障状态,其公式简洁、便于计算,可作为描述轴承状态的初始特征[22?24]。这些特征的名称如表1所示。
表1中,序号1?15为时域统计特征,16?20为频域统计特征,21?26为时频域统计特征。
为了能够全面反映滚动轴承运行状态,根据信息融合理论[25],可对3个加速度传感器和2个电涡流传感器采集到的振动信号进行特征融合。表1为一个通道信号需提取的特征参数,将其扩展至5个通道,则可得到26×5=130维的高维故障特征。
滚动轴承每种状态采集80个样本,则轴承5种运行状态可得到80×5=400个样本数据。因此,最终建立400×130的初始故障特征集,其构成如表2所示。
表2中,轴承正常、内圈故障、外圈故障、滚动体故障和保持架故障5种状态顺序排列,因此每80个样本对应轴承同一种运行状态。
3.3 特征提取方法的性能分析
利用LDA,LPP,PCA,KPCA,t?SNE和KPCA+t?SNE共6种特征提取方法分别对表2所示故障特征数据进行处理,并对各种方法提取的前3维特征进行可视化,结果如图5所示。为便于表示,不同方法提取的特征统称为主成分,图中“黑*”,“绿+”,“黄?”,“蓝□”,“红○”分别表示轴承正常、内圈故障、外圈故障、保持架故障和滚动体故障。
从图5可以看出,故障特征集经LDA处理后,各故障类型之间未能有效分离,特征提取效果最差;其他单一方法提取的特征距离也较小,甚至存在特征值重合的现象;而经KPCA+t?SNE处理后,同一类样本聚集的很近,不同类样本的类间间距较大,即它的特征提取结果明显优于LDA,LPP,PCA,KPCA,t?SNE等方法的特征提取结果。
基于图5所示6种方法的特征提取结果,计算其相应的Sb/Sw值,结果如图6所示。
由第2节分析可知,当类间间距越大、类内间距越小时,二者的比值越大,即Sb/Sw越大时,说明故障特征提取结果越好,相应方法越有效。从图6中可以看出,LDA方法的Sb/Sw值最小,KPCA+t?SNE方法的Sb/Sw值最大,其他方法的Sb/Sw值都处于二者中间。由此可见,本文提出方法能更有效地从高维故障特征集中提取出低维敏感特征集。
将上述6种方法提取的低维敏感特征集继续输入到KNNC中进行分类识别,可计算得到6种不同方法对轴承5种状态的分类准确率,同时将滚动轴承正常、内圈故障、外圈故障、滾动体故障及保持架故障分别用符号A,B,C,D,E予以表示,识别结果如表3所示。
从表3可见,LDA方法的KNNC故障平均识别率最低,而KPCA+t?SNE方法的故障平均识别率最高,且明显高于其他5种特征提取方法。
由6种方法自身特性可知,LDA,LPP,t?SNE只能挖掘数据集的局部结构信息,对数据集的全局结构信息难以有效提取;相反,PCA和KPCA只能提取数据集的全局结构信息,却无法获得数据集的局部结构信息。利用本文所提出的方法,先选取经KPCA处理后累积贡献率大于95%的前几个主成分特征,然后利用t?SNE进一步挖掘其局部流形结构,从而充分挖掘出滚动轴承故障数据的全局和局部结构信息,实现了滚动轴承故障特征的有效提取。图6和表3中的结果也表明本文方法具有更强大的特征提取能力。
3.4 变工况下的特征提取能力分析
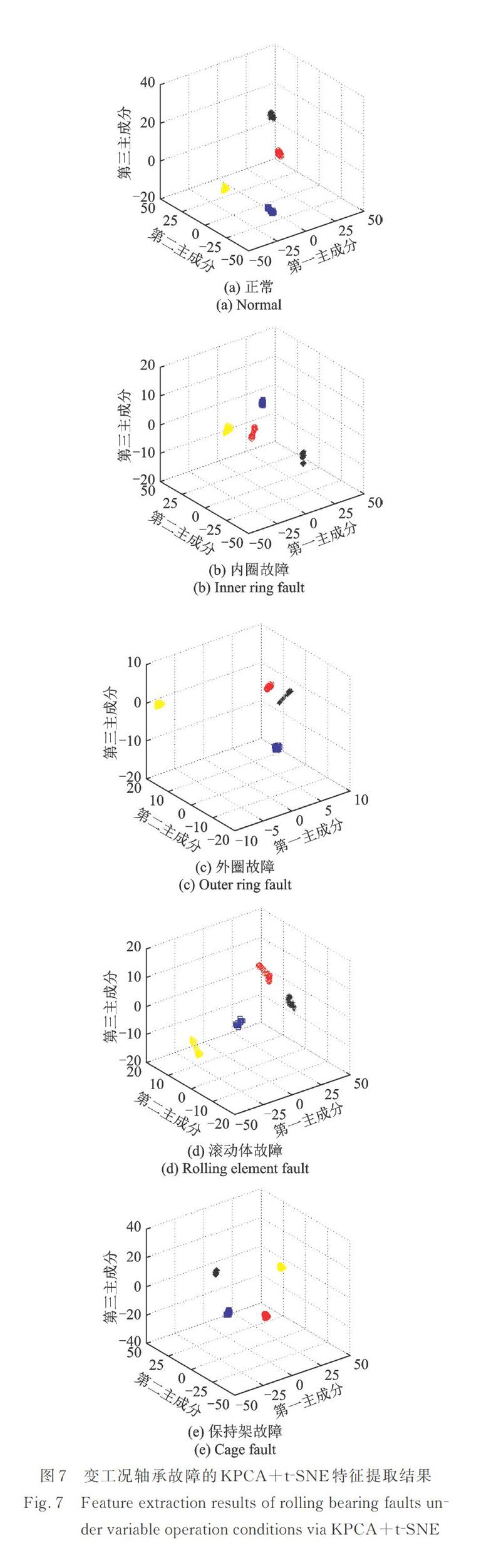
滚动轴承在实际工作时其工况通常是变化的,且同一故障在不同工况下难以有效区分[26]。为进一步验证本文提出方法的有效性,利用图2所示实验台,采集轴承内圈转速分别为2600,2800,3000,3200 r/min时5种轴承状态的振动信号并利用本文方法进行处理。记转速2600 r/min为工况1,2800 r/min为工况2,3000 r/min为工况3,3200 r/min为工况4,对同一故障不同工况下的故障信号集按图1流程进行处理,各种故障信号通过KPCA+t?SNE方法提取的前3维主成分特征如图7所示。图中“黑*”,“黄?”,“蓝□”,“红○”分别代表工况1、工况2、工况3、工况4。
从图7(a),(b),(c),(d),(e)可以看出,滚动轴承正常、内圈故障、外圈故障、滚动体故障以及保持架故障的不同工况之间能够完全分离,且很明显,它们的类内间距都很小,类间间距都较大。上述结果说明集成KPCA与t?SNE的特征提取方法能够有效获取变工况滚动轴承故障振动数据的特征信息,进一步验证了该方法强大的特征提取能力。
将6种特征提取方法分别与KNNC相结合,对轴承每种故障4个工况的数据进行分类识别,6种方法对每种故障的分类准确率如图8所示。
从图8可见,PCA等前面5种方法的分类准确率较小、曲线波动较大,而KPCA+t?SNE方法的分类准确率整体保持在90%以上,分类结果最为稳定。由此说明,本文方法不仅能够对定工况下滚动轴承不同故障的特征进行有效提取,也能够实现滚动轴承同一故障不同工况特征的准确提取。实验结果进一步证明了本文方法的有效性和广泛适用性。
3.5 方法的抗干扰能力分析
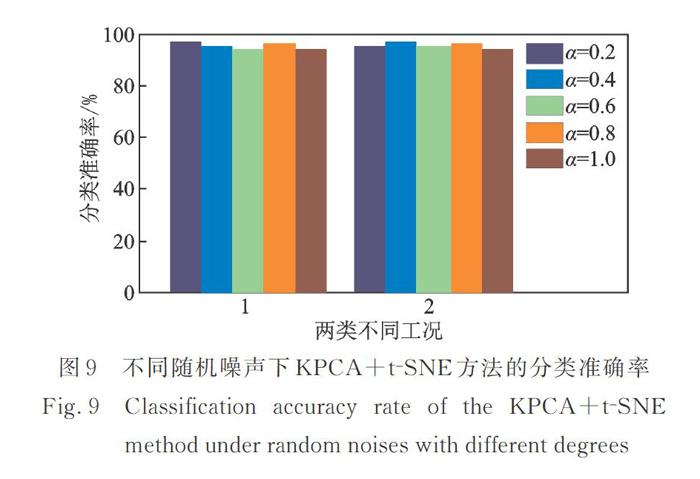
为了验证本文提出方法的抗干扰能力,对其所提取的定工况故障特征集和变工况故障特征集,同时加入干扰系数α分别为0.2,0.4,0.6,0.8,1的5种随机噪声成分[27];然后,将其分别输入到KNNC中进行分类识别,并将变工况记为“1”,定工况记为“2”,两类工况下含噪故障数据的分类准确率如图9所示。
从图9可见,特征数据在不同噪声干扰系数的情况下,本研究所提出方法的分类准确率保持稳定,并未出现较大波动,故障分类准确率整体都大于90%。由此说明,KPCA+t?SNE能够从含噪数据中提取出重要特征,抗干扰能力强,具有较高的鲁棒性。
4 结 论
1) 为从高维非敏感故障特征集中准确提取低维敏感特征子集,提出了一种集成KPCA与t?SNE的滚动轴承故障特征提取方法。该方法综合考虑了样本数据的全局与局部结构特征信息,与传统特征提取方法相比,能够避免部分重要信息的丢失。通过实验数据对方法的有效性进行了验证,结果表明本研究提出的方法能够准确提取出滚动轴承故障特征信息。
2) 通过与其他5种特征提取方法进行实验对比表明,本文提出的KPCA+t?SNE方法可准确提取轴承故障的特征信息,其类内间距、类间间距以及分类准确率都优于传统特征提取方法,且故障分类准确率都在90%以上;利用本方法对不同干扰程度的含噪故障数据进行处理,可从含噪数据中提取出重要特征信息,故障分类准确率保持稳定,抗干扰能力较强。
3) 本研究提出的方法充分考虑了数据集的全局和局部结构特征,实现了滚动轴承故障特征的准确提取,为实际轴承故障诊断提供了一种理论方法。下一步工作,将尝试对该方法进行拓展,并应用到滚动轴承复合故障/早期故障的特征提取及故障辨识中,使其能够适用于更复杂的故障诊断问题。
参考文献:
[1] 郭宝良, 段志善, 郑建校, 等. 振动机械滚动轴承单点点蚀故障诊断研究[J]. 振动工程学报, 2012, 25(5): 610?618.
Guo Baoliang, Duan Zhishan, Zheng Jianxiao, et al. Fault diagnosis of single?point pitting corrosion for rolling bearing of vibrating machine[J]. Journal of Vibration Engineering, 2012, 25(5): 610?618.
[2] Zhang M G, Ge Z Q, Song Z H, et al. Global?local structure analysis model and its application for fault detection and identification[J]. Industrial & Engineering Chemistry Research, 2011, 50(11): 6837?6848.
[3] Luo L J, Bao S Y, Gao Z L, et al. Batch process monitoring with tensor global?local structure analysis[J]. Industrial & Engineering Chemistry Research, 2013, 52(50): 18031?18042.
[4] 赵孝礼, 赵荣珍. 全局与局部判别信息融合的转子故障数据集降维方法研究[J]. 自动化学报, 2017, 43(4): 560?567.
Zhao Xiaoli, Zhao Rongzhen, A method of dimension reduction of rotor faults data set based on fusion of global and local discriminant information[J]. Acta Automatica Sinica, 2017, 43(4): 560?567.
[5] 韩敏, 李宇, 韩冰. 基于改进结构保持数据降维方法的故障诊断研究[J]. 自动化学报, 2021, 47(2): 338-348.
Han Min, Li Yu, Han Bing. Research on fault diagnosis of data dimension reduction based on improved structure preserving algorithm[J]. Acta Automatica Sinica, 2021, 47(2): 338-348.
[6] Dong S J, Luo T H, Zhong L, et al. Fault diagnosis of bearing based on the kernel principal component analysis and optimized k?nearest neighbour model[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2017, 36(4): 354?365.
[7] 马萍, 张宏立, 范文慧. 基于局部与全局结构保持算法的滚动轴承故障诊断[J]. 机械工程学报, 2017, 53(2): 20?25.
Ma Ping, Zhang Hongli, Fan Wenhui. Fault diagnosis of rolling bearings based on local and global preserving embedding algorithm[J]. Journal of Mechanical Engineering, 2017, 53(2): 20?25.
[8] 姜洪权, 王岗, 高建民, 等. 一种适用于高维非线性特征数据的聚类算法及应用[J]. 西安交通大学学报, 2017, 51(12): 50?55.
Jiang Hongquan, Wang Gang, Gao Jianmin, et al. A clustering algorithm for high?dimensional nonlinear feature data with applications[J]. Journal of Xian Jiaotong University, 2017, 51(12): 50?55.
[9] 苏祖强, 汤宝平, 姚金宝. 基于敏感特征选择与流形学习维数约简的故障诊断[J]. 振动与冲击, 2014, 33(3): 70?75.
Su Zuqiang, Tang Baoping, Yao Jinbao. Fault diagnosis method based on sensitive feature selection and manifold learning dimension reduction[J], Journal of Vibration and Shock, 2014, 33(3): 70?75.
[10] Jiang B, Ding C, Luo B. Robust data representation using locally linear embedding guided PCA[J]. Neurocomputing, 2018, 275: 523?532.
[11] Zhang Y, Li B W, Wang Z B, et al. Fault diagnosis of rotating machine by isometric feature mapping[J]. Journal of Mechanical Science and Technology, 2013, 27(11): 3215?3221.
[12] Levin K, Lyzinski V. Laplacian eigenmaps from sparse, noisy similarity measurements[J]. IEEE Transactions on Signal Processing, 2017, 65(8): 1988?2003.
[13] Lu G F, Wang Y, Zou J, et al. Matrix exponential based discriminant locality preserving projections for feature extraction[J]. Neural Networks, 2018, 97: 127?136.
[14] 梁超, 路鹏, 郜宁, 等. 基于LPP的转子振动故障特征提取方法[J]. 振动工程学报, 2018, 31(3): 539?544.
Liang Chao, Lu Peng, Gao Ning, et al. Feature extraction of rotor vibration fault based on LPP algorithm[J]. Journal of Vibration Engineering, 2018, 31(3): 539?544.
[15] Maaten L V D, Hinton G. Visualizing data using t?SNE[J]. Journal of Machine Learning Research, 2008, 9: 2579?2605.
[16] 张康, 黄亦翔, 赵帅, 等. 基于t?SNE数据驱动模型的盾构装备刀盘健康评估[J]. 机械工程学报, 2019, 55(7): 19?26.
Zhang Kang, Huang Yixiang, Zhao Shuai, et al. Health assessment of shield equipment cutterhead based on t?SNE data?driven model[J]. Journal of Mechanical Engineering, 2019, 55(7): 19?26.
[17] Retsinas G, Stamatopoulos N, Louloudis G, et al. Nonlinear manifold embedding on keyword spotting using t?SNE[C].Proceedings of the 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), IEEE Computer Society, 2017: 246?255.
[18] Song W J, Wang L Z, Liu P, et al. Improved t?SNE based manifold dimensional reduction for remote sensing data processing[J]. Multimedia Tools and Applications, 2019, 78(4): 4311?4326.
[19] Andrej G, Alexander S, Hammer B. Parametric nonlinear dimensionality reduction using kernel t?SNE[J]. Neurocomputing, 2015, 147: 71?82.
[20] 张曦, 赵旭, 刘振亚, 等. 基于核Fisher子空间特征提取的汽轮发电机组过程监控与故障诊断[J]. 中国电机工程学报, 2007, 27(20): 1?6.
Zhang Xi, Zhao Xu, Liu Zhenya, et al. Process monitoring and fault diagnosis of turbine generator unit based on feature extraction in kernel Fisher subspace[J]. Chinese Society for Electrical Engineering, 2007, 27(20): 1?6.
[21] Aslam M W, Zhu Z, Nandi A K. Automatic modulation classification using combination of genetic programming and KNN[J]. IEEE Transactions on Wireless Communications, 2012, 11(8): 2742?2750.
[22] Lei Y G, He Z J, Zi Y Y. A new approach to intelligent fault diagnosis of rotating machinery[J]. Expert Systems with Applications, 2008, 35(4): 1593?1600.
[23] 程晓涵, 汪爱明, 花如祥, 等. 24种特征指标对轴承状态识别的性能研究[J]. 振动、测试与诊断, 2016, 36(2): 351?358.
Chen Xiaohan, Wang Aiming, Hua Ruxiang, et al. Studying on property of 24 characteristic indexes to bearing state recognition[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(2): 351?358.
[24] 劉建昌, 权贺, 于霞, 等. 基于参数优化VMD和样本熵的滚动轴承故障诊断[J/OL]. 自动化学报, 1?12(2019?08?12). https://doi.org/10.16383/j.aas.190345.
Liu Jianchang, Quan He, Yu Xia, et al. Rolling bearing fault diagnosis based on parameter optimization VMD and sample entropy[J/OL]. Acta Automatica Sinica, 1?12(2019?08?12). https://doi.org/10.16383/j.aas.190345.
[25] 张明, 江志农. 基于多源信息融合的往复式压缩机故障诊断方法[J]. 机械工程学报, 2017, 53(23): 46?52.
Zhang Ming, Jiang Zhinong. Reciprocating compressor fault diagnosis technology based on multi?source information fusion[J]. Journal of Mechanical Engineering, 2017, 53(23): 46?52.
[26] 唐贵基, 庞彬. 基于时时能量阶比谱的变转速工况滚动轴承微弱故障诊断研究[J]. 振动工程学报, 2017, 30(5): 856?864.
Tang Guiji, Pang Bin. Research on fault diagnosis of rolling bearing's weak fault under variable speed conditions based on time?time energy order spectrum[J]. Journal of Vibration Engineering, 2017, 30(5): 856?864.
[27] Chen F F, Tang B P, Chen R X. A novel fault diagnosis model for gearbox based on wavelet support vector machine with immune genetic algorithm[J]. Measurement, 2013, 46(1): 220?232.
Fault feature extraction of rolling bearing integrating KPCA and t?SNE
WANG Wang?wang, DENG Lin?feng, ZHAO Rong?zhen, WU Yao?chun
(School of Mechanical and Electronical Engineering, Lanzhou University of Technology, Lanzhou 730050, China)
Abstract: The original data set of rolling bearing contains high-dimensional non-sensitive features, so a low-dimensional sensitive feature extraction method through integrating kernel principal component analysis (KPCA) and t-distributed stochastic neighbor embedding (t-SNE) is proposed in this paper. The time domain, frequency domain and time-frequency domain features of the raw rolling bearing vibration signal are calculated to construct the original high-dimensional feature data set. KPCA is used to reduce the correlation of high-dimensional data set, and the nonlinear feature subset is extracted while maximizing the global feature variance of the data set. t-SNE is employed to mine the local structure information of feature data set, and further obtain the low-dimensional sensitive feature subset with high discriminability. The low-dimensional feature subset is input into the k-nearest neighbor classifier (KNNC), and the classification accuracy and clustering results are used as the quantitative indexes to evaluate the performance of the feature extraction method. In this process, the global and local structure features of the data set are comprehensively considered and the structure information of the data itself is fully utilized, so the low-dimensional sensitive features can be accurately extracted. The proposed method is applied to the fault diagnosis of a rolling bearing test rig. By comparing the results obtained from 6 different feature extraction methods and analyzing the fault data sets under variable rotating speeds and different random noises respectively, the effectiveness of the proposed method is verified, and consequently it is actually an excellent feature extraction method for the fault recognition of rolling bearings.
Key words: fault diagnosis; rolling bearing;fault feature extraction;kernel principal component analysis;t?distribution stochastic neighbor embedding; k?nearest neighbor classifier
作者简介: 王望望(1990?),男,硕士研究生。电话:18893842635;E?mail:1475168400@qq.com
通讯作者: 邓林峰(1984?),男,博士,副教授,硕士研究生导师。E?mail:denglinfeng2002@163.com
