驱动轴系统轴向派生力的测试与计算分析方法

冯华渊　上官文斌　SUBHASHRakheja　罗勇

摘要： 以具有三销轴万向节的驱动轴系统为对象，进行轴向派生力测试，并分析驱动轴系统转速、工作角度、负载转矩和摩擦系数对轴向派生力的影响。基于赫兹接触理论与基于速度的摩擦模型，建立驱动轴系统轴向派生力计算的多体动力学模型。为了提高模型的计算精度，把球环和滚道之间的接触形状视为任意的，且把接触参数和摩擦系数视为随着工况变化而变化的变量。基于有限元分析，提出了一种计算在不同负载扭矩下球环和滚道之间接触刚度和力指数的方法。利用建立的轴向派生力计算模型和试验数据，进一步识别了多种工况下的摩擦系数和接触参数。基于识别的摩擦系数和接触参数，计算了一驱动轴系统的轴向派生力，和试验结果的对比分析表明，模型的计算精度较高。

关键词： 驱动轴系统; 轴向派生力; 三销轴万向节; 摩擦和接触; 参数识别

中图分类号： U463.21; U467.3    文献标志码： A    文章编号： 1004-4523（2021）02-0253-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.02.005

引  言

驱动轴系统是轿车传动系统中的一个重要组成部分，主要用于传递从变速器到车轮的负载转矩，同时可保证输入端和输出端在一定夹角下的等速性。通常情况下，驱动轴系统主要由3个部分组成：（1）固定式等速万向节（常采用球笼式等速万向节）：其与车轮端相连;（2）可轴向滑移式等速万向节：其与变速器端相连;（3）驱动轴：位于固定式等速万向节和可轴向滑移式等速万向节之间。

三销轴式等速万向节（三销轴万向节）是一种常见的可轴向滑移式等速万向节。由于三销轴万向节内部的摩擦特性和运动特性，三销轴万向节在工作过程中会产生一个周期性的轴向力，称为轴向派生力，此轴向力具有3阶特性[1?6]。在汽车行驶中，轴向派生力会引起汽车的抖动[5?7]，甚至会造成异响。具有三销轴万向节的驱动轴系统中，轴向派生力的影响因素很多，如何建立一个能准确表征驱动轴系统轴向派生力的模型，是驱动轴系统动态特性研究的热点和难点。

目前，对具有三销轴万向节的驱动轴系统轴向派生力的研究，主要集中于轴向派生力的测试和建模分析。

由于三销轴万向节的轴向派生力主要与其内部的摩擦有关，Lee等[1?2]開发了专用的摩擦特性测试的试验台，用于测量三销轴万向节在各种工况下的摩擦特性和滑移阻尼，并对摩擦特性进行了建模分析。Lee等[3]建立了驱动轴系统轴向派生力的测试台，研究了负载转矩、工作角度和润滑脂对轴向派生力和汽车加速抖动问题的影响。为了研究由于驱动轴系统引起的汽车怠速抖动问题，Sa等[4]建立起了驱动轴系统滑移阻力和轴向派生力的测试台，用于测量不同类型三销轴万向节的滑移阻力和轴向派生力。

在具有三销轴万向节的驱动轴系统轴向派生力的建模过程中，三销轴万向节内部的运动特性分析、摩擦力分析和接触力分析是三个重要部分。基于这三个部分，很多研究人员建立了具有三销轴万向节驱动轴系统的轴向派生力计算模型。其中，比较典型的工作有：

Serveto等[5]建立了两种具有三销轴万向节驱动轴系统的轴向派生力计算模型，用于计算驱动轴系统的轴向派生力，并且利用库仑摩擦来计算两种模型中的摩擦力，采用冲击函数（以接触刚度、力指数和穿透位移等表征法向接触力的函数）来计算模型中的接触力，但该文没有给出接触刚度和力指数的具体计算方法。Jo等[6]通过三销轴万向节的运动学分析，得到了三销轴万向节内部各接触点的法向力计算公式，采用了两种摩擦模型（纯滑动摩擦模型和同时考虑滑动和滚动的摩擦模型）来计算摩擦力，基于法向力计算公式和摩擦模型，建立了三销轴万向节轴向派生计算模型。

Lim等[8]建立了驱动轴系统动态性能分析的多体动力学模型，用于分析驱动轴系统的轴向派生力与滑移阻力和三销轴万向节各部件受到的动态力。与文献[5]相似，文中采用了库仑摩擦和冲击函数来分别计算多体动力学模型中的摩擦力和接触力，但文中没有给出接触刚度和力指数的具体计算方法;文中模型的计算精度很低，最大相对误差达到50%。Cai等[9]建立了驱动轴系统轴向派生力计算的多体动力学模型。与文献[5，8]不同的是，文中采用Lee等[2]提出的半经验动态摩擦模型来计算摩擦力，采用接触对的接触刚度、穿透位移和阻尼比等来表征法向接触力。基于三销轴万向节的运动学分析，Mariot等[10]建立了驱动轴系统的运动静力模型（摩擦模型分别采用：黏性摩擦模型和库仑摩擦模型），对比分别采用两种摩擦模型后轴向派生力计算模型的计算结果可得：利用包含库仑摩擦的轴向派生力计算模型，可计算得到3阶轴向派生力。

具有三销轴万向节的驱动轴系统轴向派生力在中国研究较少。主要研究工作有：郑娇娇等[11]基于赫兹接触理论和库仑摩擦模型，建立了具有三销轴万向节驱动轴系统的动力学模型，分析了球环所受的法向力、圆周力及其随转角和摆角的变化规律，以及由摩擦力所产生的轴向窜动力、径向力和偏转扭矩。文中的摩擦系数和接触参数参照材料碰撞参数表取得，且文中缺少实验验证。常德功教授的团队对滑移型三叉式联轴器进行了研究，发表了一系列的研究成果[12?15]。他们建立了滑移型三叉式联轴器的运动学和动力学分析的模型和方法，开展了相关的试验研究工作。在动力学的建模分析时，没有考虑滑移型三叉式联轴器内部各个部件之间的摩擦。

综上所述，在目前驱动轴系统轴向派生力的研究中，主要集中于轴向派生力的测试以及建模研究。在建模计算轴向派生力的过程中，需要获取接触对的摩擦和接触相关参数，如摩擦系数、接触刚度和力指数。在目前的研究中，主要通过拟合试验数据来获取接触对的摩擦系数和接触刚度，针对接触对的力指数的研究较少。并且，在计算轴向派生力时，如果把摩擦系数和接触参数视为常数，模型的计算误差会比较大[8]。在实际工程中，随着驱动轴系统工况的变化，三销轴式万向节内部接触对的摩擦系数和接触参数是变化的。因此，为了提高轴向派生力计算模型的精度，需要把三销轴式万向节内部接触对的摩擦系数和接触参数视为变量，并且识别这些变量随着工况变化的规律。

本文以驱动轴系统为研究对象，给出了驱动轴系统轴向派生力测试的方法，测试了一具有三销轴万向节驱动轴系统的轴向派生力与驱动轴系统的转速、负载扭矩、工作角度和润滑脂的關系。建立具有三销轴万向节驱动轴系统轴向派生力计算的多体动力学分析模型，提出了一种分析和计算不同负载扭矩下球环和滚道之间接触刚度和力指数的方法。并进一步识别了摩擦系数和接触参数随着工况变化的规律。基于识别的不同工况下的摩擦系数和接触参数，计算了一驱动轴系统在不同工况下的轴向派生力，并进行了试验验证。

1 驱动轴系统轴向派生力的测试

1.1 轴向派生力的测试方法

驱动轴系统轴向派生力测试的原理和装置图分别见图1（a）和（b）所示。测试时，液压作动器施加负载转矩，转速控制电机施加转速。在三销轴万向节与液压作动器的连接端，沿着周向均匀安装4个力传感器，传感器的安装示意图见图1（c）。当驱动轴系统在一定负载转矩和转速下旋转时，4个力传感器同时测试沿着三销轴万向节轴向的力信号。数据采集系统采集力信号，并把4个力信号的平均值作为测试得到的轴向派生力。

测试分析了不同工作角度、不同润滑脂、不同负载转矩和不同驱动轴系统转速下具有三销节万向节的驱动轴系统的轴向派生力。测试条件如表1所示。

1.2 轴向派生力的测试结果

1.2.1 不同工作角度δ下和不同润滑脂下的测试结果

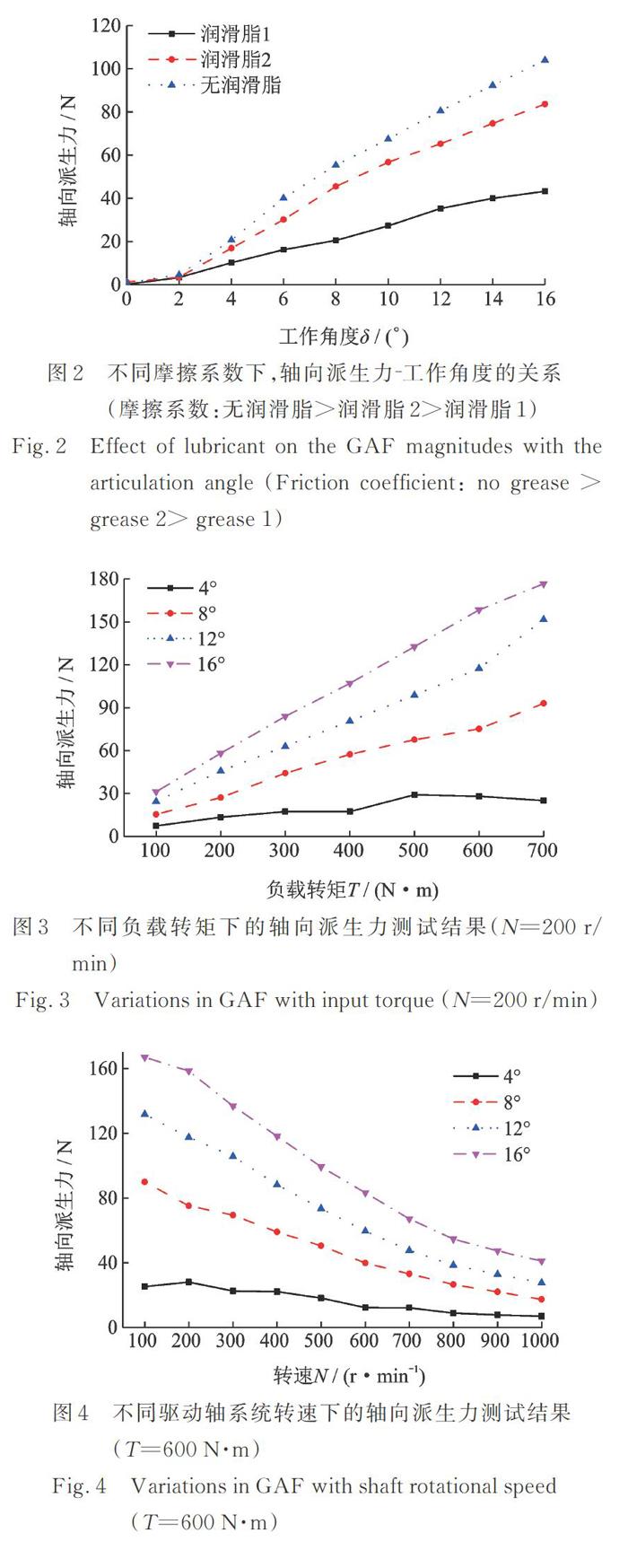
图2为在不同润滑脂下，轴向派生力与工作角度δ之间关系的测试结果（转速N和负载转矩T分别为200 r/min和300 N·m）。由图可见，随着δ增加，轴向派生力增加。使用润滑脂后，轴向派生力大幅减小，最大的减小幅度超过了60%。

1.2.2 不同负载转矩T下的测试结果

当转速N=200 r/min、工作角度δ一定时（分别为4°，8°，12°，16°），不同负载转矩T下轴向派生力的测试结果如图3所示。由图可得：T越大，轴向派生力越大，且轴向派生力与T近似成正比关系。

1.2.3 不同转速N下的测试结果

当负载转矩T=600 N·m、工作角度δ一定时（分别为4°，8°，12°，16°），不同转速N下轴向派生力的测试结果如图4所示。由图可得：N越大，轴向派生力越小;工作角度δ越高时，随着N升高，轴向派生力减小越快。

综上所述，驱动轴系统的工作角度、转速、负载转矩及三销轴式万向节内部接触对的摩擦系数对轴向派生力都有很大影响。特别是在高工作角度、高负载转矩、低转速时，驱动轴系统会产生较高的轴向派生力，此时，轴向派生力会引起汽车的抖动，甚至会造成异响[1?7]。

2 驱动轴系统的轴向派生力计算模型

2.1 轴向派生力计算模型

驱动轴系统的轴向派生力主要由三销轴万向节内部球环和滚道之间的摩擦力引起，其他部件之间的摩擦力对轴向派生力的影响较小[5]。因此，在建立驱动轴系统轴向派生力计算模型时，只考虑球环和滚道之间的摩擦力和法向接触力。

驱动轴系统轴向派生力计算的多体动力学模型如图5所示。由图5（a）可知，模型包括了5种刚体结构：驱动轴、三柱槽壳、球环、滚针和三销架。滚针简化为圆柱筒，如图5（b）所示;在球环?滚道之间建立接触和摩擦对;在球环?滚针之间建立圆柱副约束;在滚针?三销架和驱动轴?三销架之间分别建立固定副约束;在三销轴万向节端施加转动副约束和转速，负载转矩施加在驱动轴上，球笼式万向节以球副代替，如图5（c）所示。三销轴万向节模型的其他特征保持不变。

计算时，调整驱动轴轴线与三柱槽壳轴线的夹角，则可形成一定的驱动轴系统工作角度;在接触和摩擦对处输入接触参数和摩擦参数（如接触刚度、力指数、静摩擦系数和动摩擦系数）;在三销轴万向节端施加一定的转速，在驱动轴上施加一定负载转矩。由多体动力学模型，可计算沿着三销轴万向节轴线方向的力，即轴向派生力。

根据文献[2，5]和1.2节的测试分析可得：影响轴向派生力的主要因素有三销节的节圆半径（即三销节中心到滚道中心线的距离）、摩擦系数、接触参数、驱动轴的工作角度、负载扭矩和转速。其中节圆半径是影响轴向派生力的尺寸参数。节圆半径的精度较高（尺寸公差一般为0.05 mm），其对轴向派生力的影响较小。在不同运行工况（不同工作角度、负载转矩和转速）下，节圆半径可视为常数。而在不同工况下，由于三销节内部接触状态和摩擦状态的变化，接触副的接触参数和摩擦参数（如接触刚度、力指数、静摩擦系数和动摩擦系数）对计算结果的影响很大。为此下文重点研究多体动力学模型中摩擦和接触参数的确定方法。

2.2 球环-滚道之间的摩擦模型和法向接触力模型

采用基于速度的摩擦模型来表征球环与滚道之间的摩擦。基于速度的摩擦模型的摩擦系数表达式为[16?17]

式中  μs为静摩擦系数;v为球环与滚道之间的相对速度;C，B，E为常数，它们与摩擦模型的形状有关[16]，由测试得到摩擦系数与相对速度的关系和式（1）的计算关系，通过最小二乘方法拟合可获得C，B，E。

获得C，B，E之后，则可描述摩擦系数和速度的关系，如图6所示。由图可见，随着相对速度的增加，摩擦系数先增加到峰值μs（静摩擦系数），最后下降并趋于μd（动摩擦系数）。其中，摩擦系数增加到达峰值μs时的相对速度为Vs，摩擦系数由峰值μs下降到μd时的相对速度为Vd。由于相对速度Vs和Vd对轴向派生力的影响较小[5，8，18]，假定相对速度Vs和Vd为常数，它们不随工况变化。

当球环和滚道接触时，球环和滚道的法向受力示意图如图7所示。其中，F为法向压力，Fn为法向接触力，?为穿透位移。法向接触力和穿透位移之间的关系可用冲击函数表征[5，8]，冲击函数为

当假定接触对的接触形状为圆形且不考虑接触阻尼时，可由式（7）计算接触法向力，此时力指数n为1.5，接触刚度k可由式（6）计算。静摩擦参数和动摩擦参数可由式（1）拟合数据得到。把接触刚度、力指数、静摩擦系数和动摩擦系数等参数输入轴向派生力计算模型，则可计算不同工况下的轴向派生力。此时，接触参数和摩擦系数被视为常数，与工况无关。

但在实际工程中，由于工况不同，球环和滚道之间的接触和摩擦状态不同，接触参数和摩擦参数可能随着工况而变化。因此，为了提高模型的计算精度，需要进一步研究球环和滚道之间接触刚度和力指数的方法（接触形状为任意形状），以及识别摩擦系数和接触参数随着工况变化的规律。

2.3 球环-滚道之间接触刚度和力指数的计算方法

基于有限元分析，本文提出了一种计算球环和滚道之间接触刚度和力指数的方法，具体如下

（1）球环与三柱槽壳的有限元建模

由于三销轴万向节的对称性，只分析单个球环与三柱槽壳的接触，如图8（a）所示。由于球环与三柱槽壳在圆周方向的相对角度位移不大，故可把球环相对于三柱槽壳的转动角度位移简化成球环沿X方向的线位移，利用线位移载荷进行加载，如图8（b）所示。在网格划分时，网格的大小为2 mm，网格类型为四面体网格。约束三柱槽壳尾端的6个自由度，如图8（c）所示。三柱槽壳的材料为40Cr，其弹性模量和泊松比分别设为195 GPa和0.24;球环材料为GCr15，其弹性模量和泊松比分别设为200 GPa和0.24。

（2）球环和滚道之间接触刚度和力指数的拟合方法

由于有限元分析计算的过程是一个准静态过程，冲击函数（式（2））中穿透位移的时间微分? ˙可近似为0，因此由式（2）简化得到

F_n=k?^n （8）

在不同负载转矩下，球环施加在三柱槽壳滚道上的力不同，球环和三柱槽壳之间的穿透位移也不相同。因此，在一定负载转矩下，根据下式计算球环施加在三柱槽壳滚道上的力，以此力作为有限元分析的载荷，从而通过有限元分析得到力和位移曲线。

F=T_0/r （9）

式中  T0为负载转矩，r为三销节的节圆半径，F为球环施加在三柱槽壳滚道上的法向压力。

利用有限元分析得到的力和位移关系和由式（8）表征的力和位移关系，由最小二乘方法拟合得到接触刚度、力指数。

（3）球环和滚道之间接触刚度和力指数的拟合结果

当负载转矩为500 N·m时（载荷约为：19500 N），某球环和三柱槽壳滚道的接触刚度和力指数拟合结果如图9所示。由图可知：由式（8）拟合得到的力和位移曲线与有限元分析计算的力和位移关系的相关系数R2为0.99，拟合精度较高。

在不同负载转矩下，球环和三柱槽壳滚道的接触刚度和力指数的拟合结果如图10所示。由图可得，随着负载转矩的增大，拟合的接触刚度和力指数都减小。因此，当负载转矩不同时，球环和三柱槽壳滚道之间的接触刚度和接触形状等是不同的。

2.4 球环-滚道之间摩擦系数与接触参数的进一步识别

由2.2和2.3节分析可知，在不同驱动轴系统运行工况下，由于三销轴万向节内部的摩擦状态和接触状态等的变化，球环和滚道之间的摩擦系数和接触参数会有一定变化。因此，为了提高轴向派生力计算模型的计算精度，需要识别各种工况下摩擦系数和接触参数。根据赫兹理论，接触刚度主要与接触体的材料特性以及外部作用力等有关。因此，对于一驱动轴系统，假设接触刚度只与负载转矩有关。根据2.3节分析，接触刚度随着负载转矩变化的曲线见图10。在确定接触刚度后，需要进行不同工况下摩擦系数和力指数的识别。球环和滚道之间摩擦系数（静摩擦系数和动摩擦系数）和力指数的识别数学模型如下

式中  q=（?s，?d，n）为需要识别的参数向量，xi代表某一工况，FM（xi）为在xi工况下的测试结果，FE（q）为对应于xi工况下的轴向派生力计算模型计算结果，μsu和μsl分别为静摩擦系数μs的上下限，μdu和μdl分别为动摩擦系数μd的上下限，nu和nl分别为力指数n的上下限。

3 计算实例

基于式（10），可识别得到一款驱动轴系统在不同工况下的摩擦系数和力指数（见附录）。建立另一驱动轴系统的多体动力学模型，该驱动轴系统的三销轴万向节尺寸减小，球环的形状改为椭圆形，其他零部件的尺寸和特征不变。当驱动轴系统转速为200 r/min、负载转矩分别为300和600 N·m时，识别接触和摩擦参数前后计算的轴向派生力与测试结果如图11所示。由图可得，与识别参数前（各参数视为常数，具体计算方法见2.2节）相比，识别参数后计算的轴向派生力与测试结果更加吻合。当工作角度在驱动轴系统的安装角度附近时（4o?8o），识别参数后轴向派生力的计算值和测试值的相对误差约为14%。因此，利用本文摩擦系数和接触参数的计算和识别方法，可使轴向派生力计算模型的计算精度有较大提高。

4 结  论

（1）驱动轴系统轴向派生力随着工作角度的增大呈近似线性增长，而润滑脂的种类对其增长速度影响很大;轴向派生力随着负载转矩的增大也呈近似线性增长，但随着驱动轴系统转速的增加而减小。

（2）提出了一种球环和滚道之间接触刚度和力指数的计算方法，通过计算可得：接触刚度和力指数随着驱动轴负载转矩的增加而减小;在不同负载扭矩下，球环和滚道之间的接触形状是不同的。

（3）與识别接触和摩擦参数前相比（把各参数视为常数，即各参数与工况无关），基于本文提出的接触刚度和力指数的计算方法以及识别的摩擦系数和接触参数，可使模型的计算精度有较大的提高。

参考文献：

[1] Lee C H， Polycarpou A A. Experimental investigation of tripod constant velocity （CV） joint friction[C]. SAE 2006 World Congress & Exhibition， 2006.

[2] Lee C H， Polycarpou A A. A phenomenological friction model of tripod constant velocity （CV） joints[J]. Tribology International， 2010， 43（4）：844-858

[3] Lee K H， Lee D W， Chung J H， et al. Design of generated axial force measurement tester for tripod constant velocity joints under shudder condition[J]. Journal of Mechanical Science & Technology， 2014， 28（10）：4005-4010.

[4] Sa J S， Kang T W， Kim C M. Experimental study of the characteristics of idle vibrations that result from axial forces and the spider positions of constant velocity joints[J]. International Journal of Automotive Technology， 2010， 11（3）：355-361.

[5] Serveto S， Mariot J P， Diaby M. Modelling and measuring the axial force generated by tripod joint of automotive drive-shaft[J]. Multibody System Dynamics， 2008， 19（3）：209-226.

[6] Jo G H， Kim S H， Kim D W， et al. Estimation of generated axial force considering rolling-sliding friction in tripod type constant velocity joint[J]. Tribology Transactions， 2018，61（5）：889-900.

[7] Hayama Y， Nozaki T， Nakakouji M， et al. NVH analysis using full vehicle multi body dynamic model[J]. NTN Technical Review， 2005， 73：92-97.

[8] Lim Y H， Song M E， Lee W H， et al. Multibody dynamics analysis of the drive-shaft coupling of the ball and tripod types of constant velocity joints[J]. Multibody System Dynamics， 2009， 22（2）：145-162.

[9] Cai Q C， Lee K H， Song W L， et al. Simplified dynamics model for axial force in tripod constant velocity joint[J]. International Journal of Automotive Technology， 2012， 13（5）：751-757.

[10] Mariot J P， Knevez J Y， Barbedette B. Tripod and ball joint automotive transmission kinetostatic model including friction[J]. Multibody System Dynamics， 2004， 11（2）：127-145.

[11] 鄭娇娇，郭常宁，雍耀伟，等.三球销式等速万向节受力及仿真分析[J].机械强度， 2015， 37 （1）：114-121.

Zheng Jiaojiao， Guo Changning， Yong Yaowei， et al. The force and simulation analysis of tripod constant velocity universal joint[J]. Journal of Mechanical Strength， 2015， 37 （1）：114-121.

[12] Wang X F， Chang D G， Wang J Z. Kinematic investigation of tripod sliding universal joints based on coordinate transformation[J]. Multibody System Dynamics， 2009， 22（1）：97-113.

[13] Wang X F， Chang D G. Numerical analysis on lubricating properties of tripod sliding universal joints[J]. Tribology Transactions， 2008， 52（1）：86-95.

[14] 王学锋，常德功，王江忠.滑移型三叉式联轴器运动学建模[J]. 农业机械学报， 2009， 40（9）：7-11.

Wang Xuefeng， Chang Degong， Wang Jiangzhong. Kinematic model of tripod sliding universal joints[J]. Transactions of the Chinese Society of Agricultural Machinery， 2009， 40（9）：7-11.

[15] 常德功， 李松梅. 双径向轴承安装三叉杆滑块式万向联轴器机构的运动分析[J]. 机械工程学报， 2015， 51（13）：218-226.

Chang Degong， Li Songmei. Kinematic analysis of the trigeminal sliding universal joint mechanism installed twin radial bearings[J]. Chinese Journal of Mechanical Engineering， 2015， 51（13）：218-226.

[16] Pennestrì E， Rossi V， Salvini P， et al. Review and comparison of dry friction force models[J]. Nonlinear Dynamics， 2016， 83（4）：1785-1801.

[17] Wang Dexin， Rui Yuting. Simulation of the stick-slip friction between steering shafts using ADAMS/PRE[C]. International ADAMS User Conference， Orlando， USA， 2000.

[18] Spencer W， Bouzit D， Pace J， et al. Study of stick-slip friction between plunging driveline[C]. SAE Technical Papers， 2015-01-2171.

[19] Johnson K L. Contact Mechanics[M]. London： Cambridge University Press， 1985.

Measurement and calculation methods of axial generated force for automotive drive shaft systems

FENG Hua?yuan1， SHANGGUAN Wen?bin1， SUBHASH Rakheja1， LUO Yong2

（1. School of Mechanical and Automotive Engineering， South China University of Technology， Guangzhou 510641， China;

2. Zhejiang Xianglong Machinery Co. Ltd.， Ningbo 315300， China）

Abstract： Taking a drive shaft system with a tripod joint and a ball joint as a research object， the axial force generated by the tripod joint is measured. The influence of the shaft rotating speed， the articulation angle， the input torque and the friction coefficient on the generated axial force （GAF） is investigated. Based on Hertz contact theory and the velocity-based friction model， a multi-body dynamic model for calculating the GAF of a drive shaft system is established. To enhance the calculation accuracy of the model， the contact shape between the roller and the track inside the tripod joint is regarded as arbitrary， and the contact parameters and friction coefficient are regarded as variables that change with the operating conditions. Based on the finite element method， a method for calculating contact stiffness and force exponent between rollers and tracks is presented， and the friction coefficient and force exponent under various operating conditions are further identified by using the measured data. Based on the identified friction and contact parameters， a multi-body dynamic model of another drive shaft system is established， and the GAF is calculated and compared with the experiments. It is concluded that the calculated GAF and the measured GAF agrees well， which indicates the calculation accuracy of the GAF calculation model is high.

Key words： drive shaft system; generated axial force; tripod joint; friction and contact; parameters identification

作者簡介：冯华渊（1993?），男，博士研究生。电话：18819452314; E?mail： 2728455611@qq.com

通讯作者：上官文斌（1963?），男，教授。电话：18820072208; E?mail： sgwb@scut.edu.cn

附录：