改进TSA降噪与平方包络谱分析的故障特征提取

郭远晶　金晓航　魏燕定　杨友东

摘要： 为实现旋转机械设备故障诊断，提出基于相关性检测的振动信号改进时域同步平均（Time Synchronous Averaging，TSA）降噪方法，并利用平方包络谱提取故障特征。在采样振动信号中任取一段参考子信号，令参考子信号从振动信号初始时间开始，沿时间轴逐点滑动至终了时间，同时计算参考子信号与其在振动信号中遮掩子信号之间的相关系数;利用步长迭代算法获取相关系数最优阈值，选择与参考子信号相关系数大于最优阈值的所有遮掩子信号作为总体同步信号，平均计算后获得降噪的目标信号;对目标信号进行平方包络谱分析。仿真信号、齿轮和轴承振动信号的分析结果表明，所提出的方法能够有效用于旋转机械设备的振动信号降噪与故障特征提取。

关键词： 故障诊断; 时域同步平均; 相关系数; 步长迭代算法; 平方包络谱

中图分类号： TH165+.3; TN911.7    文献标志码： A    文章编号： 1004-4523（2021）02-0402-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.02.021

引  言

旋转机械设备出现故障损伤时，振动信号中通常包含有规律性的故障特征，其提取对于设备故障诊断具有重要意义。但由于噪声干扰、传递路径衰减、多振源耦合等因素[1]，往往需要对振动信号进行降噪处理，如滤波器降噪、小波阈值降噪、SVD降噪以及经验模态分解降噪等，才能顺利提取出故障特征。此外，在旋转机械设备平稳运行工况下，适应于振动信号的周期性变化特征，时域同步平均（Time Synchronous Averaging，TSA）降噪方法也得到了广泛应用[2?7]。

振动信号TSA降噪的关键在于参与平均计算的各段振动信号要保持同步，即无相位差。目前保持振动信号同步的方法主要有按整数周期截取信号和时标脉冲触发同步采样[8]。按整数周期截取信号的方法需要获取振动信号的准确周期[7]，但这并不是一件容易的事情，原因在于旋转机械设备的转速通常不能保持时刻恒定，尤其是在故障损伤状态下，转速的波动使振动信号没有一个严格稳定的周期，因此，按照一个固定周期对振动信号进行截断，会出现相位误差累积效应[9]，影响降噪效果。时标脉冲触发同步采样则需要在参考轴上安装转速计或光电编码器，输出时标脉冲触发振动信号的同步采样或者插值重采样[2，5，10?11]。此类方法能够保证采样振动信号的准确同步，但需要额外增加硬件成本，并且在很多实际应用场合中，转速计或光电编码器的安装也并非易事[12]，因此，此类方法的应用也受到一定限制。

为了获取时域同步振动信号参与TSA降噪，本文从旋转机械设备上采集的振动信号中选取一段参考子信号，令参考子信号从振动信号的初始时间开始，沿时间轴滑动至终了时间，期间参考子信号不断地在振动信号中遮掩一段等长度的子信号，同时计算参考子信号与遮掩子信号之间的相关系数;然后利用步长迭代算法获取相关系数的最优阈值;最后选择与参考子信号相关系数大于最优阈值的所有遮掩子信号作为总体同步信号，平均计算后获得降噪的目标信号。对目标信號进行平方包络谱分析，提取故障特征，判别旋转机械设备故障状态。

1 TSA降噪原理

旋转机械设备运行时的振动信号为y（t），采样时间间隔为Δt，则采样振动信号为y（kΔt），记作y（k），k=0，1，…，N（N为振动信号采样数据点数）。若y（k）由周期为NT（NT为一个时间周期内的采样数据点数）的特征信号s（k）和白噪声sn（k）组成，即

式中  fr为齿轮转频，fm为齿轮啮合频率，N为冲击特征个数，An为第n个冲击特征的最大幅值，[tn ，tn+1）表示第n个冲击特征的持续时间范围。

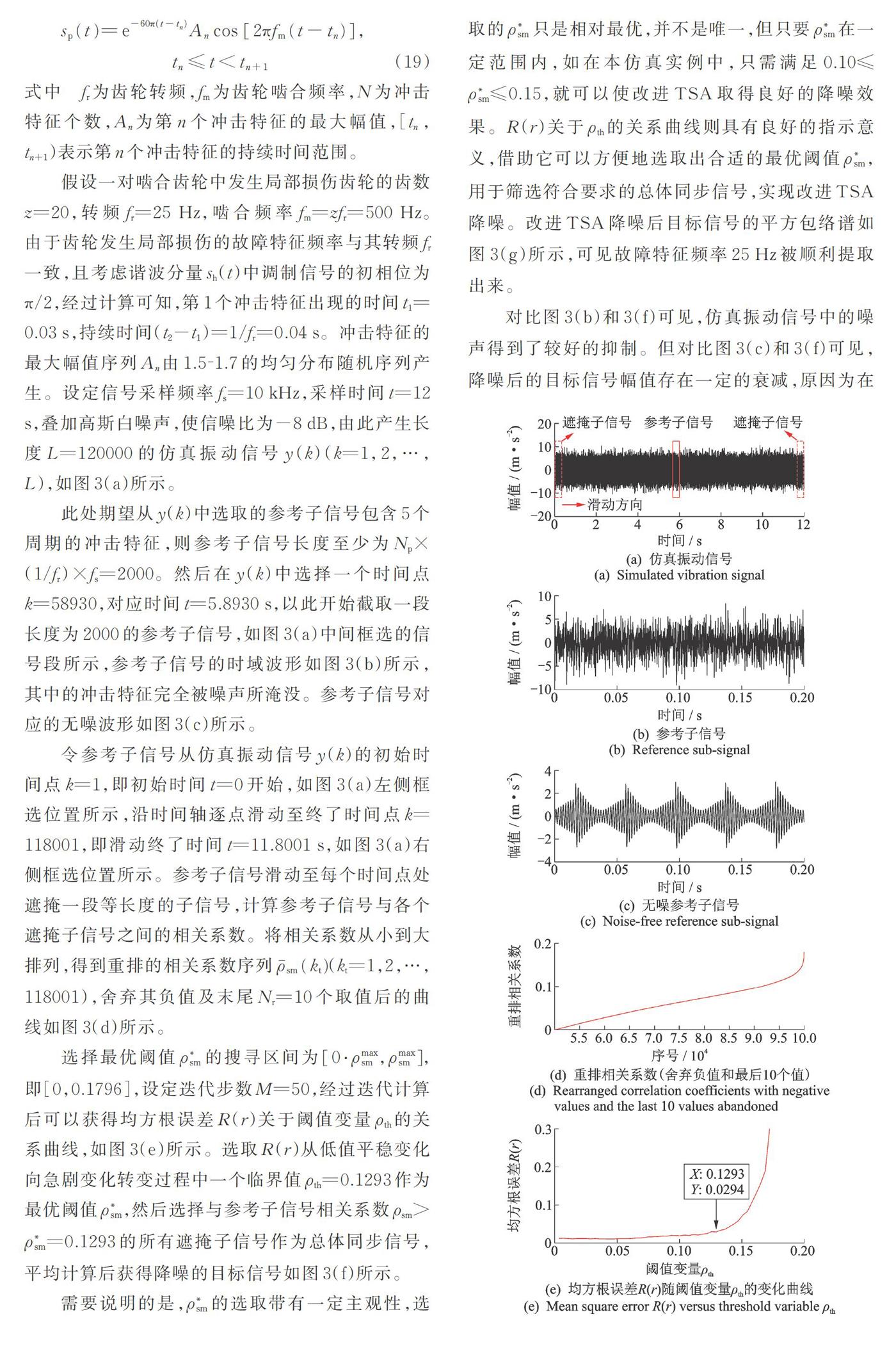
假设一对啮合齿轮中发生局部损伤齿轮的齿数z=20，转频fr=25 Hz，啮合频率fm=zfr=500 Hz。由于齿轮发生局部损伤的故障特征频率与其转频fr一致，且考虑谐波分量sh（t）中调制信号的初相位为π/2，经过计算可知，第1个冲击特征出现的时间t1=0.03 s，持续时间（t2-t1）=1/fr=0.04 s。冲击特征的最大幅值序列An由1.5?1.7的均匀分布随机序列产生。设定信号采样频率fs=10 kHz，采样时间t=12 s，叠加高斯白噪声，使信噪比为-8 dB，由此产生长度L=120000的仿真振动信号y（k）（k=1，2，…，L），如图3（a）所示。

此处期望从y（k）中选取的参考子信号包含5个周期的冲击特征，则参考子信号长度至少为Np×（1/fr）×fs=2000。然后在y（k）中选择一个时间点k=58930，对应时间t=5.8930 s，以此开始截取一段长度为2000的参考子信号，如图3（a）中间框选的信号段所示，参考子信号的时域波形如图3（b）所示，其中的冲击特征完全被噪声所淹没。参考子信号对应的无噪波形如图3（c）所示。

令参考子信号从仿真振动信号y（k）的初始时间点k=1，即初始时间t=0开始，如图3（a）左侧框选位置所示，沿时间轴逐点滑动至终了时间点k=118001，即滑动终了时间t=11.8001 s，如图3（a）右侧框选位置所示。参考子信号滑动至每个时间点处遮掩一段等长度的子信号，计算参考子信号与各个遮掩子信号之间的相关系数。将相关系数从小到大排列，得到重排的相关系数序列ρ ?_sm （k_t）（kt=1，2，…，118001），舍弃其负值及末尾Nr=10个取值后的曲线如图3（d）所示。

需要说明的是，ρ_sm^*的选取带有一定主观性，选取的ρ_sm^*只是相对最优，并不是唯一，但只要ρ_sm^*在一定范围内，如在本仿真实例中，只需满足0.10≤ρ_sm^*≤0.15，就可以使改进TSA取得良好的降噪效果。R（r）关于ρth的关系曲线则具有良好的指示意义，借助它可以方便地选取出合适的最优阈值ρ_sm^*，用于筛选符合要求的总体同步信号，实现改进TSA降噪。改进TSA降噪后目标信号的平方包络谱如图3（g）所示，可见故障特征频率25 Hz被顺利提取出来。

对比图3（b）和3（f）可见，仿真振动信号中的噪声得到了较好的抑制。但对比图3（c）和3（f）可见，降噪后的目标信号幅值存在一定的衰减，原因为在总体同步信号中，以参考子信号为参考，虽然超前的遮掩子信号与滞后的遮掩子信号之和无相位差，但两者在幅值上存在一定的相互抵消，因此两者求和之后再求平均，获得的幅值要比参考子信号小。

为进一步验证改进TSA降噪方法的有效性，在y（k）中再任选一个时间点k=12689，对应时间t=1.2689 s，以此开始截取一段长度同样为2000的参考子信号，按前述相同步骤获取降噪后的目标信号如图4（a）所示，其平方包络谱如图4（b）所示。在y（k）中改选一个时间点k=102371，对应时间t=10.2371 s，按相同方法获取的降噪后目标信号及其平方包络谱分别如图5（a）和5（b）所示。通过对比可以发现，参考子信号选取的时间点不同，对最终获取目标信号的降噪效果没有影響，只是目标信号的相位可能会发生改变，但这对目标信号平方包络谱中故障特征的提取并无影响。

5 实际振动信号分析

5.1 齿轮故障振动信号分析

齿轮故障振动信号取自一台风力发电机，其齿轮箱中一个小齿轮发生轮齿断裂损伤故障，如图6所示。该小齿轮的齿数z=32，额定转速n=1770 r/min，转频fr=29.5 Hz，故障特征频率fg=fr=29.5 Hz，啮合频率fm=z·fn=960 Hz，振动信号采样频率fs=97656 Hz，采样得到的一段振动信号如图7（a）所示。

由于该小齿轮的故障特征频率为29.5 Hz，此处期望截取的参考子信号中至少包含6个故障冲击特征，那么参考子信号的长度至少为6×（1/29.5）×fs=19531。因此，在采样的振动信号中任选一个时间点k=50836，对应时间为t=0.5206 s，以此开始截取一段长度为19854的参考子信号，时域波形如图7（b）所示，其中噪声较大，故障特征并不显著。令参考子信号从采样振动信号初始时间开始，沿时间轴逐点滑动，计算参考子信号与各时间点处遮掩子信号之间的相关系数。滑动结束后，将相关系数从小到大排列，得到重排相关系数序列，舍弃其负值及末尾Nr=10个取值后的曲线如图7（c）所示。

选择最优阈值ρ_sm^*的搜寻区间为[0.3ρ_sm^max， ρ_sm^max]，即[0.0997，0.3324]，设定迭代步数M=100，迭代计算后获得均方根误差R（r）关于阈值变量ρth的关系曲线，如图7（d）所示。选取R（r）在低值平稳变化过程中最小值处的阈值ρth=0.1928作为最优阈值ρ_sm^*，然后选择与参考子信号相关系数ρsm>ρ_sm^*=0.1928的所有遮掩子信号作为总体同步信号，平均计算后获得降噪的目标信号，如图7（e）所示，可见其中显著的周期性故障冲击特征。

对降噪后的目标信号进行平方包络谱分析，如图7（f）所示，可见小齿轮故障特征频率fg及其倍频（2?13）×fg被清晰地提取出来。目标信号的包络谱如图7（g）所示，故障特征频率fg及其倍频的谱线不如平方包络谱清晰，因此，相比于包络谱，平方包络谱在振动信号分析中具有一定的优势。

作为比较，采用基于周期分段的传统TSA降噪方法对采样振动信号进行处理，获得的降噪信号如图8（a）所示，其平方包络谱与包络谱分别如图8（b）和8（c）所示。从时域上讲，由于齿轮故障损伤会引起转速波动，振动信号的周期并非严格恒定，按周期分段截取的各段振动信号存在一定的相位误差，且相位误差具有累计效应，相比于改进TSA降噪方法，传统TSA降噪方法获取的目标信号降噪不够彻底，存在较多的高频分量，其中的周期性故障冲击特征不太容易被识别，信号幅值也存在较大程度的衰减。从频域上讲，改进TSA降噪方法与传统TSA降噪方法对于故障特征频率的提取效果基本相同，且平方包络谱的故障特征频率及其倍频谱线要比包络谱更加清晰可辨。

5.2 轴承故障振动信号分析

轴承故障振动信号取自Case Western Reserve University轴承数据中心。选择试验台驱动端的NTN滚动轴承为研究对象，其内滚道上有一直径为0.7112 mm（0.028"），深度为1.27 mm（0.050"）的局部损伤故障。在试验台运行过程中，驱动电机功率为2.2 kW，转速为1730 r/min，加载电机施加3 N·m载荷，轴承内圈的故障特征频率fBPFI=123 Hz。振动数据采样频率为12 kHz，采样到的一段振动信号如图9（a）所示。

在采样振动信号中任选一个时间点k=20185，对应时间为t=1.6821 s，以此开始截取一段长度为2000的参考子信号，如图9（b）所示，其中故障冲击特征并不显著。令参考子信号从采样的振动信号初始时间开始，沿时间轴逐点滑动，计算参考子信号与遮掩子信号之间的相关系数。滑动结束后获得参考子信号与所有遮掩子信号之间的相关系数，将其从小到大排列后得到重排相关系数序列，舍弃其负值及末尾Nr=10个取值后的曲线如图9（c）所示。

选择最优阈值ρ_sm^*的搜寻区间为[0?ρ_sm^max，ρ_sm^max]，即[0，0.5822]，设定迭代步数M=100，迭代计算后获得均方根误差R（r）关于阈值变量ρth的关系曲线，如图9（d）所示。选取R（r）从低值平稳变化向急剧增大变化转变的一个临界值ρth=0.4366作为最优阈值ρ_sm^*，然后选择与参考子信号相关系数ρsm>ρ_sm^*=0.4366的所有遮掩子信号作为总体同步信号，平均计算后获得降噪的目标信号如图9（e）所示，可见噪声得到了较好的抑制，周期性特征非常显著。降噪后目标信号的平方包络谱如图9（f）所示，明显可见轴承内圈的故障特征频率fBPFI及其倍频（2?5）×f_BPFI。降噪后目标信号的包络谱如图9（g）所示，故障特征频率fBPFI及其倍频的谱线也基本清晰可辨，但不如平方包络谱突出。

作为比较，采用传统TSA降噪方法对轴承的采样振动信号进行处理，获得降噪的目标信号如图10（a）所示。从该目标信号中能够大致看出信号的周期性，但难以辨别出周期性的故障冲击特征，原因在于轴承故障损伤引起转速波动，导致采样振动信号的周期并非严格恒定，按周期分段截取的各段时域同步信号在求和过程中存在较大的相位误差累计效应。相比于改进TSA降噪方法，传统TSA降噪方法获取的目标信号降噪不够彻底，存在较多的高频成分以及故障特征频率的0.5倍、1.5倍、2.5倍等分数倍频成分，这从传统TSA降噪目标信号的平方包络谱（如图10（b）所示）与包络谱（如图10（c）所示）中也可以看出来。虽然传统TSA降噪结合平方包络谱或包络谱也能够提取出故障特征频率，但由于故障特征频率分数倍频成分的存在，对故障特征频率识别有一定的干扰，影响故障判别。

6 结  论

（1）提出一种基于相关性检测的改进TSA降噪方法，该方法在旋转机械設备的采样振动信号中任选一段参考子信号，令参考子信号在采样振动信号中逐点滑动，计算参考子信号与遮掩子信号之间的相关系数;然后利用步长迭代算法获取相关系数的最优阈值;最后选择与参考子信号相关系数大于最优阈值的所有遮掩子信号作为总体同步信号，平均计算后可以获得降噪效果良好的目标信号。

（2）改进TSA降噪方法成功应用于齿轮与轴承故障振动信号的处理，降噪后得到的目标信号经过平方包络谱分析，能够有效提取出齿轮与轴承的故障特征频率，从而实现旋转机械设备故障诊断。

（3）改进TSA降噪方法对旋转机械设备转速的稳定性以及振动信号的平稳性没有严格要求，无需获取振动信号的准确周期，避免了振动信号按周期分段而导致的相位误差累积效应;无需转速传感器，硬件成本低、应用场合广，具有较好的适用性。

参考文献：

[1] 熊国良，胡俊锋，陈慧，等. 基于SK-NLM包络的滚动轴承故障冲击特征增强[J]. 仪器仪表学报，2016， 37（10）：2176-2184.

Xiong Guoliang， Hu Junfeng， Chen Hui， et al. Rolling bearing fault impact feature enhancement based on spectral kurtosis and non-local means[J]. Chinese Journal of Scientific Instrument， 2016， 37（10）： 2176-2184.

[2] Ahamed N， Pandya Y， Parey A. Spur gear tooth root crack detection using time synchronous averaging under fluctuating speed[J]. Measurement， 2014， 52： 1-11.

[3] Ha J M， Youn B D， Oh H， et al. Autocorrelation-based time synchronous averaging for condition monitoring of planetary gearboxes in wind turbines[J]. Mechanical Systems and Signal Processing， 2015， 70-71： 161-175.

[4] Li H， Xu F， Liu H， et al. Incipient fault information determination for rolling element bearing based on averaging reassigned wavelet scalogram[J]. Measurement， 2015， 65： 1-10.

[5] Roy S K， Mohanty A R， Kumar C S. Fault detection in a multistage gearbox by time synchronous averaging of the instantaneous angular speed[J]. Journal of Vibration and Control， 2016， 22（2）： 468-480.

[6] Camerini V， Coppotelli G， Bendisch S， et al. Impact of pulse time uncertainty on synchronous average： Statistical analysis and relevance to rotating machinery diagnosis[J]. Mechanical Systems and Signal Processing， 2019， 129： 308-336.

[7] 龙海军，孙灿飞，莫固良. 直升机振动检测通用算法的研究与实现[J]. 振动、测试与诊断，2016，36（3）：524-528.

Long Haijun， Sun Canfei， Mo Guliang. Research and implementation of general algorithm for helicopter vibration detection[J]. Journal of Vibration， Measurement & Diagnosis， 2016， 36（3）：524-528.

[8] 邵毅敏，周晓君，欧家福. 变周期信号的时域同步平均新算法[J]. 振动工程学报，2009，22（5）：497-502.

Shao Yimin， Zhou Xiaojun， Ou Jiafu. A algorithm of time domain averaging for fluctuant-period signal[J]. Journal of Vibration Engineering， 2009， 22（5）：497-502.

[9] 沈国际，陶利民，徐永成. 时域同步平均的相位误差累积效应研究[J]. 振动工程学报，2007，20（4）：335-339.

Shen Guoji， Tao Limin， Xu Yongcheng. Research on phase error accumulation effect of time synchronous averaging[J]. Journal of Vibration Engineering， 2007， 20（4）：335-339.

[10] 罗德扬. 时域同步平均原理与应用[J]. 振动、测试与诊断，1999，19（3）：202-207.

Luo Deyang. Principals and applications of time domain synchronous averaging[J]. Journal of Vibration， Measurement & Diagnosis， 1999， 19（3）： 202-207.

[11] 吕琛，宋希庚，邹积斌. 基于DSP的振动信号阶比与时域同步平均分析[J]. 振动与冲击，2002，21（2）：53-57.

L? Chen， SONG Xigeng， ZOU Jibin. DSP-based order domain and time domain synchronous averaging analysis of vibration signal[J]. Journal of Vibration and Shock， 2002， 21（2）： 53-57.

[12] Combet F， Gelman L. An automated methodology for performing time synchronous averaging of a gearbox signal without speed sensor[J]. Mechanical Systems and Signal Processing， 2007， 21（6）： 2590-2606.

[13] 何正嘉，刘雄，屈梁生. 信号时域平均原理和应用[J]. 信号处理，1986，2（4）：46-53.

He Zhengjia， Liu Xiong， Qu Liangsheng. The principle and application of signal time domain average[J]. Signal Processing， 1986， 2（4）： 46-53.

[14] 郭远晶，魏燕定，周晓军. 基于STFT时频谱系数收缩的信号降噪方法[J]. 振动、测试与诊断，2015，35（6）：1090-1096.

Guo Yuanjing， Wei Yanding， Zhou Xiaojun. Signal denoising method based on STFT time-frequency spectrum coefficients shrinkage[J]. Journal of Vibration， Measurement & Diagnosis， 2015， 35（6）： 1090-1096.

[15] Antoni J. Cyclic spectral analysis of rolling-element bearing signals： Facts and fictions[J]. Journal of Sound and Vibration， 2007， 304（3-5）： 497-529.

[16] Borghesani P， Pennacchi P， Chatterton S. The relationship between kurtosis- and envelope-based indexes for the diagnostic of rolling element bearings[J]. Mechanical Systems and Signal Processing， 2014， 43（1-2）： 25-43.

Fault feature extraction based on improved TSA denoising and squared envelope spectrum

GUO Yuan-jing1， JIN Xiao-hang2， WEI Yan-ding3， YANG You-dong1

（1. Zhijiang College， Zhejiang University of Technology， Shaoxing 312030， China;

2. College of Mechanical Engineering， Zhejiang University of Technology， Hangzhou 310023， China;

3. Key Laboratory of Advanced Manufacturing Technology of Zhejiang Province， Zhejiang University， Hangzhou 310027， China）

Abstract： In order to achieve the fault diagnosis of the rotating machine equipment， a method based on improved time synchronous averaging （TSA） denoising using correlation detection and fault features extracting using squared envelope spectrum is proposed. A reference sub-signal is arbitrarily taken from the sampled vibration signal. The reference sub-signal starts from the initial time of the vibration signal and moves point by point along the time axis to the end time. Meanwhile， the correlation coefficient between the reference sub-signal and its masking sub-signal in the vibration signal is calculated. The correlation coefficient optimal threshold are obtained using the step iterative algorithm. All the masking sub-signals whose correlation coefficients are greater than the optimal threshold are selected as overall synchronous signals whose arithmetic average is calculated for the denoised target signal. The target signal analysis is achieved using squared envelope spectrum. The analysis results of the simulated signal， gear and rolling bearing fault vibration signals have shown that the proposed method is an efficient implementation for rotating machine vibration signal denoising and fault feature extraction.

Key words： fault diagnosis; time synchronous averaging; correlation coefficient; step iterative algorithm; squared envelope spectrum

作者簡介： 郭远晶（1987-），男，博士，讲师。电话：（0575）81112562;E-mail：gyjyn@126.com