双向非均质黏性阻尼土中桩基扭转振动频域阻抗解答与分析

崔春义　梁志孟　王本龙　许成顺　姚怡亦

摘要： 基于三维连续黏性阻尼介质理论和径向多圈层复刚度传递模型，综合考虑桩周土径向非均质效应和纵向成层性，建立双向非均质土体中桩基扭转振动简化分析模型。采用拉普拉斯变换和复刚度传递法求解得出土体位移形式解，进而利用桩?土耦合条件将该形式解耦合进桩身动力平衡方程中，并通过扭转阻抗传递法推导得出桩顶扭转阻抗解析解答。将该解退化并分别与均质土及径向非均质土中的解答进行对比验证其合理性。在此基础上，通过参数化分析探讨了桩周土施工扰动程度和扰动范围、扩颈及缩颈缺陷对桩顶扭转阻抗的影响规律，可为具体工程实践提供理论指导和参考作用。

关键词： 桩基; 扭转振动; 双向非均质; 复刚度传递模型; 施工扰动

中图分类号： TU473.1    文献标志码： A    文章编号： 1004-4523（2021）02-0311-10

DOI：10.16385/j.cnki.issn.1004-4523.2021.02.011

引 言

针对动力机器基础和海上钻井平台等工程环境，桩基础除受竖向、水平荷载外，往往还承受不可忽视的扭转动载作用。在桩基打桩过程中，受其打桩挤土效应的影响，迫使桩周土体产生一定的不均匀性，即径向非均质效应[1?2]。为深入探究非均质效应对桩基振动特性产生的影响，近些年来，国内外诸多学者针对桩基扭转振动专题开展了一系列工作，取得了较为丰富的研究成果。

首先，Veletsos等[3?4]基于平面应变假定，求解出了径向非均质土中桩基扭转阻抗解析表达式。初步探讨了施工扰动效应对桩基扭转振动特性的影响规律。Doston等[5]假定内部区域土体的剪切模量为指数变化函数，进一步推导得出径向非均质土中桩基受纵向和扭转荷载作用下的解析表达式。在此基础上，Novak等[6?7]将地基划分为内外两部分区域，进而发展求解了能够简化考虑桩侧土软化效应的桩基扭转阻抗解析表达式。Ei Naggar[8]严格将内部扰动区域划分为无数个圈层，通过圈层间复刚度递推得出了考虑桩周土径向非均质性的桩土耦合扭转振动频域解析解答。尚守平等[9]将桩周土划分为非线性黏弹性内域和线弹性外域，并考虑土层应力、位移沿深度变化，采用等效线性方法推导出了考虑桩周土非线性的桩基扭转动力阻抗函数。Wu等[10]提出环向剪切复杂刚度传递模型，利用剪切复合刚度传递法和阻抗函数传递法，给出了径向非均质滞回阻尼土中楔形桩在受扭转振动频域解析表达式。Zhang等[11]则基于三维连续介质模型，通过圈层间复刚度递推求得桩周土体对桩体作用的复刚度，进而利用桩土间的连续条件推导得出了桩基扭转振动的扭转阻抗解析解答。

以上研究均围绕桩周土体的径向非均质效应模型展开，而对于纵向成层土体中桩基扭转振动问题，国内外学者也进行了相关性研究。Guo和Randolph[12]将桩周土体视为纵向非均质土层，采用荷载传递法，求解得出纵向成层土中桩基扭转阻抗解析解答。Militano和Rajapakse[13]利用阻抗矩阵法，研究了层状地基中桩在扭转和轴向荷载作用下的动力响应问题。陈胜立等[14]通过Hankel积分变换和传递矩阵法，推导出了成层土在扭转荷载作用下单桩振动力阻抗解析解答。邹新军等[15?16]将桩周非均质土看作随深度呈指数和幂函数两种分布模式，基于平衡原理和剪切位移法，推导出了桩周土弹塑性状态下的桩基扭转阻抗解析解答。靳建明等[17]考虑桩周土体纵向成层性，基于阻抗函数传递法，递推得出桩基扭转阻抗解析表达式。Wu等[18]同时考虑桩周土纵向成层性及桩端虚拟土桩效应，基于三维连续介质理论，利用拉普拉斯变换和阻抗函数传递法，推导出了任意扭转激振下桩基扭转阻抗解析解答。

不难看出，多数已有研究成果仅从纵向或径向分别考虑桩周土非均质性对桩基扭转振动的影响，且土体阻尼考量上大多采用滞回阻尼模型。而对于桩基受瞬态激振作用下的时域响应问题，其土体阻尼力与振幅和应變率有关，此时宜用黏性阻尼模型更为合理[19?27]。因此，本文基于弹性连续介质动力学理论，综合考虑施工扰动效应和纵向成层性，采用黏性阻尼土体模型和阻抗函数传递法，针对径向非均质、纵向成层黏性阻尼土中受任意激振扭矩作用下桩基扭转振动进行频域阻抗求解与分析。

1 定解问题力学模型建立

1.1 简化力学模型及基本假设

桩?土耦合系统力学模型简图如图1所示。其中，桩?土耦合扭转振动系统根据桩体和土层性质的不同沿纵向共分为m层，自系统底部由下往上依次编号为1，2，…，i，…，m段，各层段厚度分别为l1， l2，…，li，…，lm，且各层段顶部距桩顶距离分别为h1，h2，…，hi，…，hm。第i层段桩半径、截面面积、扭转惯量和弹性模量分别为r_i1，A_i^p，J_i^p和E_i^p，桩端黏弹性支承系数为k^p，δ^p。

同时，将第i层段桩周土体划分为两部分区域，一部分是厚度为b_i的内部区域，且沿径向划分m^'个圈层;另一部分为径向无限大的均质介质外部区域。内部区域第j圈层土体密度、黏性阻尼系数、剪切模量以及土层底部黏弹性支承常数分别为ρ_ij^s，c_ij^s，G_ij^s和k_1j^s，δ_1j^s，圈层间界面处的半径为r_ij。桩顶受任意激振扭矩m_0 （t）的作用，第i层段桩周土对桩身的摩阻力为f_i^s，各纵向层段相互作用简化为分布式黏弹性Voigt体，第i-1层段与第i层段间的Voigt体弹簧系数和阻尼系数分别为k_ij^s，δ_ij^s;第i+1层与第i层段间的Voigt体弹簧系数和阻尼系数分别为k_（（i+1）j）^s，δ_（（i+1）j）^s。

假设条件如下：

（1）各段桩身假定为均质等截面弹性体，桩体底部为黏弹性支承;

（2）内部扰动区域土体各圈层为均质、各向同性黏弹性体;

（3）桩?土耦合系统满足线弹性和小变形条件，桩土界面完全接触且无脱开滑移现象。

3.1 解答合理性验证

为了验证本文推导求解所得桩基扭转振动频域解析解的合理性，首先，将本文径、纵双向非均质黏性阻尼土体模型退化成均质黏性阻尼土体模型（m→0，ξ_i^s=1），然后将本文双向非均质黏性阻尼土退化至径向非均质滞回阻尼土情况（m→0、黏性阻尼系数取为0），最后分别与已有相关解答进行退化验证分析。具体地，胡昌斌等[23]基于黏性阻尼模型和三维连续介质模型，给出了均质地基中桩基扭转阻抗解析解，本文均质退化解与胡昌斌等[23]对比验证结果如图2所示。Zhang等[11]则考虑桩周土体径向非均质性，基于滞回阻尼模型求解得到桩基扭转阻抗解析解，本文径向非均质退化解与Zhang等[11]（滞回阻尼比取为0）对比验证情况如图3所示。综合图2和3不难看出，本文推导所得扭转阻抗退化解答曲线分别与胡昌斌解[23]和Zhang解[11]中的解析解答曲线吻合良好。

3.2 桩顶扭转阻抗影响因素分析

为了探究桩侧土径向施工扰动对桩顶扭转阻抗的影响规律，选取施工软化程度和硬化程度工况如表1所示。

图4所示为土体内部区域软化程度对桩顶扭转动刚度和扭转动阻尼的影响。由图可见，桩顶扭转阻抗曲线振幅随土体内部区域软化程度升高而增大，且扭转阻抗曲线共振频率随软化程度的加大仅产生微小的影响。

图5所示为土体内部区域硬化程度对桩顶扭转动刚度和扭转动阻尼的影响情况。不难看出，土体内部区域硬化程度越高，桩顶扭转阻抗曲线振幅越小。同样地，与土体内部区域软化程度影响规律相似，土体内部区域硬化程度对桩顶扭转阻抗的共振频率影响甚微。

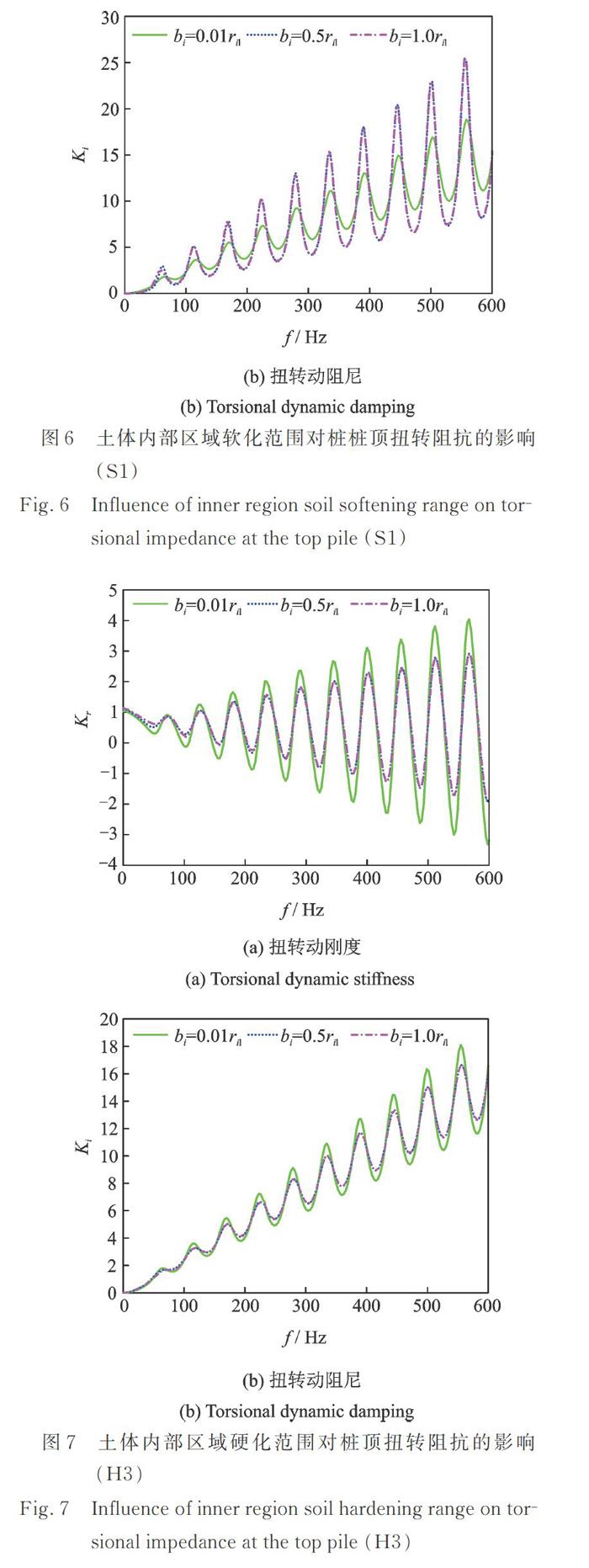
图6所示为土体内部软化区域范围对桩顶扭转动刚度和扭转动阻尼的影响情况。由图可见，随着桩周土软化区域范围的扩大，桩顶扭转阻抗振幅幅值水平逐渐增大，而幅值水平随着软化区域范围增大出现明显衰减现象，当软化范围达到一定数值后（本文中当b_i=0.5r_i1时），软化范围再增加则对桩顶扭转阻抗曲线的影响基本无影响。特别地，土体内部软化区域范围对桩顶扭转阻抗共振频率的影响可忽略。

图7所示为土体内部硬化区域范围对桩顶扭转动刚度和扭转动阻尼的影响情况。不难看出，随着土体内部硬化区域范围的扩大，桩顶转动刚度和扭转动阻尼振幅幅值水平逐渐减小。同样地，幅值水平随着硬化区域范围增大出现明显衰减现象，当硬化范围达到一定数值后（本文中当b_i=0.5r_i1时），硬化范围再增加则对桩顶转动刚度和扭转动阻尼的影响基本可以忽略。此外，土体内部硬化区域范围对桩顶扭转阻抗共振频率也可忽略。

为进一步探究桩身缩颈和扩颈对桩顶扭转动刚度和扭转动阻尼的影响规律，本文假定在距桩顶9 m处存在一段长为2 m的桩颈突变段，并定义该突变段桩身半径与相邻段桩身半径的比值为桩颈突变系数λ_R（λ_R<1代表縮颈，λ_R>1代表扩颈）。

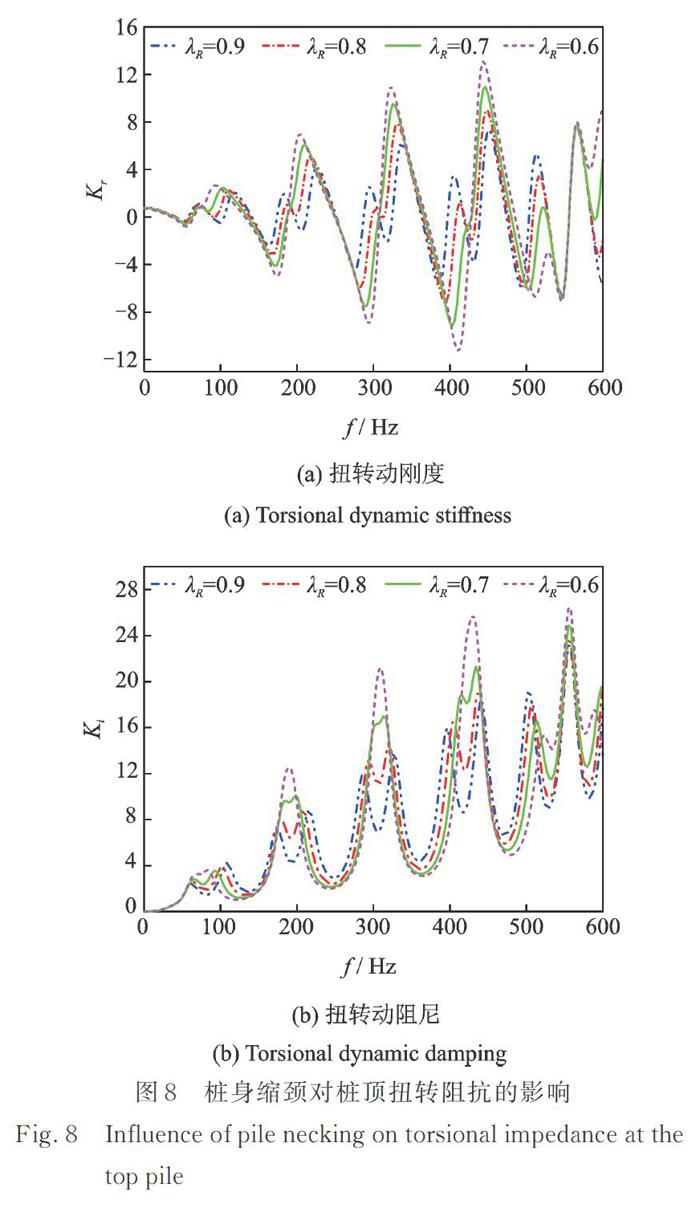
图8所示为桩身缩颈程度对桩顶扭转阻抗的影响情况。由图可见，相对于等截面桩而言，缩颈桩桩顶扭转动刚度和扭转动阻尼曲线均呈现出大、小峰值交替情况。随着桩颈突变系数λ_R的增大，即缩颈程度降低，大、小峰幅值差和峰值幅值水平均变小。

图9所示为桩身扩颈程度对桩顶扭转动刚度和扭转动阻尼的影响情况。由图可见，相对于等截面桩而言，扩颈桩桩顶扭转动刚度和扭转动阻尼曲线均呈现出大、小峰值交替特征。并且，随着桩颈突变系数λ_R的增大，即扩颈程度增高，大、小峰幅值差和峰值幅值水平均变大。

4 结 论

本文基于土体三维连续介质理论和黏性阻尼模型，综合考虑桩周土径向施工扰动效应和纵向成层性，采用径向多圈层复刚度传递法，针对径向非均质、纵向成层黏性阻尼土中受任意激振扭矩作用下的桩基进行频域阻抗求解与分析，计算分析结果表明：

（1） 通过将所得双向非均质黏性阻尼土中桩基扭转解答与已有解进行对比分析，多因素退化验证了其合理性和精度;

（2） 随着内部区域土体软（硬）化程度的加大，扭转阻抗曲线振幅明显增大（减小），但内部区域土体软（硬）化程度对扭转阻抗曲线共振频率的影响可以忽略;

（3） 随着内部区域土体软（硬）化范围扩大，桩顶扭转阻抗曲线振幅逐渐增大（减小），但当软（硬）化范围增加到一定数值（本文中当b_i=0.5r_i1时）后，此种影响效应趋于稳定;

（4） 缩（扩）颈桩桩顶扭转阻抗曲线均呈现大、小峰值交替现象，且桩颈突变系数越大，桩顶扭转阻抗曲线大、小峰的幅值差也越小（大）。

参考文献：

[1] Novak M， Han Y C. Impedances of soil layer with boundary zone[J]. Journal of Geotechnical Engineering， 1990， 116（6）：1008-1014.

[2] Han Y C， Sabin G C W. Impedances for radially inhomogeneous viscoelastic soil media[J]. Journal of Engineering Mechanics， 1995， 121（9）：939-947.

[3] Veletsos A S， Dotson K W. Impedances of soil layer with disturbed boundary zone[J]. Journal of Geotechnical Engineering， 1986， 112（3）：363-368.

[4] Veletsos A S，Dotson K W. Vertical and torsional vibration of foundations in inhomogeneous media[J]. Journal of Geotechnical Engineering，1988，114（9）：1002-1021.

[5] Dotson K W， Veletsos A S. Vertical and torsional impedances for radially inhomogeneous viscoelastic soil layers[J]. Soil Dynamics & Earthquake Engineering， 1990， 9（3）：110-119.

[6] Novak M， Howell J F. Torsional vibrations of pile foundations[J]. Journal of the Geotechnical Engineering Division， 1977， 103：271-285.

[7] Novak M， Sheta M. Approximate approach to contact problems of piles [C]. Proceedings of the Geotechnical Engineering Division， American Society of Civil Engineering National Convention， Florida， 1980： 53-79.

[8] Ei Naggar M H. Vertical and torsional soil reactions for radially inhomogeneous soil layer[J]. Structural Engineering & Mechanics， 2000， 10（4）：299-312.

[9] 尚守平， 任 慧， 曾裕林，等. 樁与土非线性耦合扭转振动特性分析[J]. 中国公路学报， 2009， 22（5）：41-47.

Shang Shouping， Ren Hui， Zeng Yulin， et al. Analysis of dynamic behaviors of pile-soil nonlinear coupling torsional vibration[J]. China Journal of Highway and Transport， 2009，22（5）：41-47.

[10] Wu W B， Jiang G S， Lü S H， et al. Torsional dynamic impedance of a tapered pile considering its construction disturbance effect[J]. Marine Georesources & Geotechnology， 2016， 34（4）：321-330.

[11] Zhang Z， Pan E. Dynamic torsional response of an elastic pile in a radially inhomogeneous soil[J]. Soil Dynamics & Earthquake Engineering， 2017， 99：35-43.

[12] Guo W， Randolph M F. Torsional piles in non-homogeneous media[J]. Computers and Geotechnics， 1996，19（4）：265-287.

[13] Militano G， Rajapakse R K N D. Dynamic response of a pile in a multi-layered soil to transient torsional and axial loading[J]. Geotechnique， 1999，49（1）： 91-109.

[14] 陈胜立， 寿汉平. 传递矩阵法分析层状地基中桩的扭转变形[J]. 岩土力学， 2004， 25（A2）： 178-180+186.

Cheng Shengli， Shou Hanping. Analysis of torsional response of a single pile embedded in layered soil with transfer matrix method[J].Rock and Soil Mechanics， 2004， 25（A2）： 178-180+186.

[15] 邹新军， 徐洞斌， 王亚雄，等. 非均质地基中单桩受扭弹塑性分析[J]. 土木工程学报， 2015，48（11）：103-110.

Zou Xinjun， Xu Dongbin， Wang Yaxiong， et al. Torsional elasto-plastic analysis of single piles in heterogeneous ground[J]. China Civil Engineering Journal， 2015，48（11）：103-110.

[16] 邹新军， 赵灵杰， 徐洞斌，等. 双层非均质地基中单桩受扭弹塑性分析[J]. 岩土工程学报， 2016， 38（5）：828-836.

Zou Xinjun， Zhao Lingjie， Xu Dongbin， et al. Elastic-plastic torsional behavior of single pile in double-layered non-homogeneous subsoil[J]. Chinese Journal of Geotechnical Engineering， 2016， 38（5）：828-836.

[17] 靳建明， 张智卿. 成层土中管桩的扭转振动特性研究[J]. 应用基础与工程科学学报， 2015， 23（4）： 782-791.

Jin Jianming， Zhang Zhiqing. Dynamic torsional response of a pipe pile embedded in layered soil[J].Journal of Basic Science and Engineering， 2015，23（4）：782-791.

[18] Wu W， Liu H， Naggar M H E， et al. Torsional dynamic response of a pile embedded in layered soil based on the fictitious soil pile model[J]. Computers and Geotechnics， 2016， 80：190-198.

[19] 胡海巖. 结构阻尼模型及系统时域动响应[J]. 振动工程学报， 1992，6（1）：8-16.

Hu Haiyan. Structural damping model and system dynamic response at time domain[J]. Journal of Vibration Engineering， 1992，6（1）：8-16.

[20] 廖振鹏. 工程波动理论导论[M].北京：科学出版社， 2002.

Liao Zhenpeng. Introduction to Wave Motion Theories in Engineering[M]. Beijing： Science Press， 2002.

[21] 胡昌斌， 张 涛. 桩与粘性阻尼土耦合扭转振动时域响应研究[J]. 振动工程学报， 2006， 19（3）：404-410.

Hu Changbin， Zhang Tao. Time domain torsional response of dynamically loaded pile in viscous damping soil layer[J].Journal of Vibration Engineering， 2006， 19（3）：404-410.

[22] 张 涛， 胡昌斌. 桩土相互作用时端承桩桩顶扭转复刚度特性研究[J]. 福州大学学报， 2006， 34（3）：409-414.

Zhang Tao， Hu Changbin. Study on torsional complex stiffness at the top of end bearing pile considering the effect of soil-pile interaction[J]. Journal of Fuzhou University， 2006， 34（3）：409-414.

[23] 胡昌斌， 张 涛. 考虑桩土耦合作用时桩基扭转振动特性研究[J]. 工程力学， 2007， 24（3）：147-153.

Hu Changbin， Zhang Tao. Soil-pile interaction in torsional vibrations of a pile in viscious damping soil layer[J].Engineering Mechanics， 2007， 24（3）：147-153.

[24] 崔春义，孟 坤，武亚军，等.考虑竖向波动效应的径向非均质黏性阻尼土中管桩纵向振动响应研究[J].岩土工程学报， 2018， 48（8）： 1434-1443.

Cui Chunyi， Meng Kun， Wu Yajun， et al. Dynamic response of vertical vibration of pipe piles in soils with radial inhomogeneousity and viscous damping considering vertical wave effect[J]. Chinese Journal of Geotechnical Engineering， 2018， 48（8）： 1434-1443.

[25] Cui Chunyi， Meng Kun，Xu Chengshun， et al. Effect of radial homogeneity on low-strain integrity detection of a pipe pile in a viscoelastic soil layer[J].International Journal of Distributed Sensor Networks， 2018，14（10）：1-7.

[26] CUI Chunyi， MENG Kun， WU Yajun， et al. Dynamic response of pipe pile embedded in layered visco-elastic media with radial inhomogeneity under vertical excitation[J]. Geomechanics and Engineering， 2018， 16（6）： 609-618.

[27] 崔春义， 孟 坤， 武亚军， 等. 非均质土中不同缺陷管桩纵向振动特性研究[J]. 振动工程学报， 2018，31（4）：707-717.

Cui Chunyi， Meng Kun， Wu Yajun， et al.Vertical  dynamic response of differ-defective pipe pile embedded in inhomogeneous soil[J]. Journal of Vibration Engineering， 2018， 31（4）：707-717.

Frequency-domain analysis and solution of torsional impedance of piles in viscous damping soil with both radial and longtudinal inhomogeinety

CUI Chun-yi1， LIANG Zhi-meng1， WANG Ben-long1， XU Cheng-shun2， YAO Yi-yi1

（1. Department of Civil Engineering， Dalian Maritime University， Dalian 116026， China; 2. Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education， Beijing University of Technology， Beijing 100124， China）

Abstract： Based on the three-dimensional continuum theory of viscous damping soil and the radial annular complex stiffness transfer model， a simplified analytical model for torsional vibration of piles in viscoelastic soil is established by considering the effects of both radial and longtudinal inhomogeinety of surrounding soil. The solution of torsional vibration displacement of surrounding soil is obtained by using Laplace transform and complex stiffness transfer method， then the form is coupled into the dynamic balance equation of the pile by using the complete coupling condition of pile-soil， and the analytical solution of torsion impedance of pile top is derived by the method of torsional impedance transfer. Furthermore， the obtained analytical solution for torsional impedance at the top of pile is degraded and compared with the existing solutions to verify its rationality. Based on that， an extensive parametric analysis is also conducted to discuss the influence of the disturbance degree， disturbance range of surrounding soil， necking and expanding of pile on the torsional impedance at the top of pile， which can provide reference and guide to related engineering practice.

Key words： pile foundation; torsional vibration;bidirectional heterogeneous;complex stiffness transfer model;construction disturbance

作者簡介： 崔春义（1978-），男，教授，博士生导师。电话：（0411）84723186; E-mail：cuichunyi@dlmu.edu.cn