盾构机姿态调整算法及仿真研究
2021-06-10薛永健
薛永健

摘要:针对工程用的盾构机械在掘进的过程中的姿态问题,在分析传统掘进姿态调整问题的基础上,提出一种基于BP的专家控制方法。在该方法中,首先提出盾构机掘进的运动学模型,从而分析盾构机掘进的原理;其次构建基于BP+专家系统的控制方法,通过BP神经网络的学习能力为专家系统提供实例,而通过专家系统的实例,直接对盾构机姿态进行控制。最后,通过仿真验证了上述方法的可行性,为工程用盾构机掘进提供了实践参考。
关键词:盾构机;BP神经网络;专家系统;姿态控制
中图分类号:U455.3+9 文献标识码:A 文章编号:1001-5922(2021)02-0192-04
在隧道挖掘等大型地下工程中经常要用到盾构机。现阶段隧道工程中,土压平衡盾构机是使用率最高、使用范围最广的机械,其前端加装的密封土舱具有稳定的切削面,在不断向前掘进的过程中,刀盘不断切削土体,液压缸同步推进,机身沿着预定轨迹向前掘进。可见,在土压平衡盾构机的掘进过程中,要想实现掘进轨迹与隧道设计轴线保持一致,就必须做好盾构机姿态的精确预测及控制。本研究则在分析盾构机姿态影响因素的基础上,尝试构建一个基于神经网络的姿态调整算法,通过姿态的预测修正盾构机运行的方向,从而提高盾构机掘进的精度。
1问题的提出
盾构机在掘进时,地层条件相对均匀,且盾构机会采取直线掘进的方式进行施工。由于地层条件变化不大,因此盾构机在作业过程中承受的由地层造成的载荷是相对稳定的。可由于盾构机自身结构特征,在重力作用下容易出现“低头”趋势。此外,由于盾构机自身因素的影响,包括其左右受力不均,以及外壳的摩擦力矩与刀盘转矩不平衡等,很容易造成盾构机姿态参数发生规律性变化。为解决该问题,传统的做法是在工作状态下通过全站仪实时检测偏航角和俯仰角,并将检测结果反馈给控制系统。控制系统通过调节推进液压缸的压力,实现盾構机的姿态纠偏。同时盾构机为实现滚转角的有效纠偏,在每次掘进施工后,每次拼装管片前,都必须执行反转刀盘这一操作。可基于控制系统的纠偏方式时效性差,而手动调节容易诱发局部受力过大的问题。如何借助现有的智能算法对盾构机的姿态进行纠偏和调整,对化解盾构机掘进过程难题具有积极作用。结合以上问题,笔者认为在结合盾构机负载模型的基础上,引人神经网络在学习能力方面的优势,构建一个基于神经网络的专家控制系统,从而实时修正盾构机掘进方向。
2盾构机负载模型构建
在盾构机工作中,要保障盾构机按照设计的轴线运行,就需要分析盾构机在掘进过程中的可能受力问题。而研究认为,盾构机在掘进中与自身的结构、地质条件等有很大的关系,包括自身重力(F1)、盾尾作用力(F2)、盾尾千斤顶作用力(F3)、正面土体阻力(F4)、盾构机周围土体作用力(F5)、后接台车牵引阻力(F6)等作用。根据动量定理,得到:
3神经网络的专家系统构建
3.1构建思路
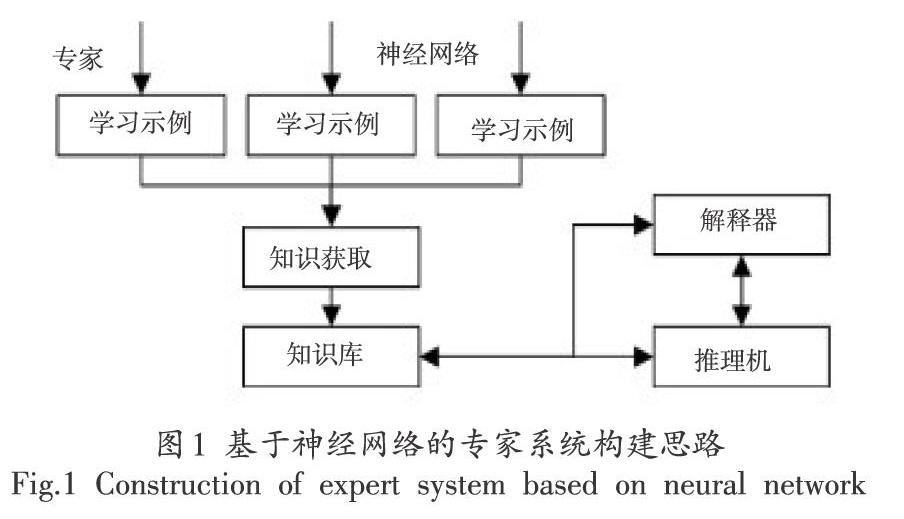
在专家系统的构建中,充分利用专家系统和神经网络的优势。其中通过神经网络的学习能力构建实例,而专家系统则利用实例,为盾构机参数的调节提供基础。具体用图1表示。在这个过程中,神经网络专家系统存储掘进施工过程中的设备状态信息和地层条件数据,从而对盾构机在当前地层条件下的姿态进行预测。如果盾构机掘进的地层条件有所改变,只需要把新的地层条件数据输入系统,即可快速确定盾构机在新的地层参数下的应有姿态。
3.2神经网络设计
3.2.1网络层数的选择
从理论上来说,神经网络能够逼近任何有理函数,该网络包含线性输出层、线性隐含层以及偏差等部分。单隐层的网络可以对闭区间内所有的连续函数进行逼近,由此推进,基于3层网络能够实现各种形式的维到维的映射。一般来说,要想提高精度、减小误差,可行的办法有两个,一是增加层数,二是增加隐藏层中神经元的数量。由于增加层数会导致原本复杂的网络更加复杂,进而使网络权值的训练时间更长,降低工作效率,故一般不采用增加层数的方法。所以,提高隐含层中的神经元数量就成为了提高精度的优选办法。基于此,本文建立3层神经网络。
3.2.2层数设计
输入层的主要用途是输入各类已接收的数据信息,输出层的主要作用是输出经过处理后的最终结果。一般来说,输人层和输出层的设计主要关联于应用问题的具体情况,应用问题的输入数决定了神经网络的输入个数,应用问题的输出数目决定了输出层的神经元个数。
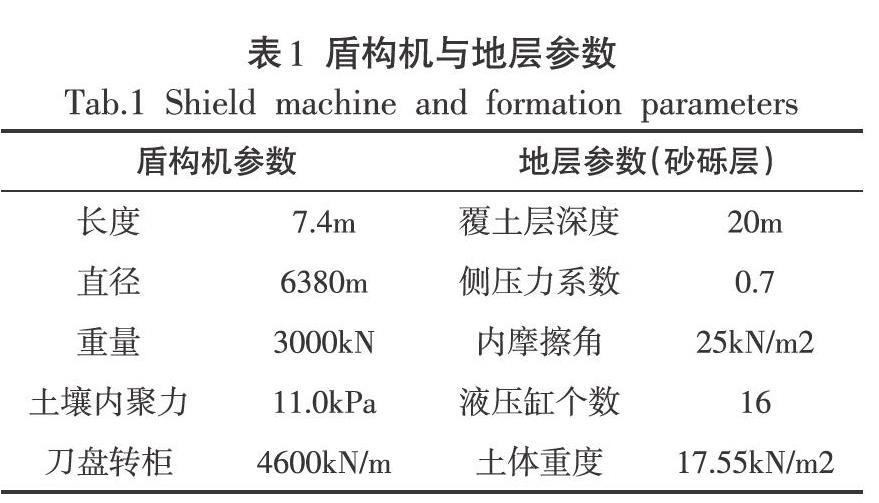
输入层的输入参数主要如表1所示。
输出层提供最终的处理结果,主要是滚转角、俯仰角和偏航角。
基于地层条件参数,根据盾构机在进行挖掘工作时的受力分布情况,本文设定输入层有13个神经元,并设定输出层的神经元数量是3个。
在进行数据处理之前,为提高网络训练的效率,本文首先对神经网络的输入、输出数据进行了预处理。通过比较Matlab内置主成分分析、标准化处理以及归一化处理等多种方法,在权衡以后,本文最终选定了归一化处理法对数据进行预处理。
“归一化”指的是把拥有多个尺度、分属不同区间的样本矢量的各个分量划人相应的区间内,由此,可以利用统一尺度对样本的各个分量进行表征。目前,在神经网络的训练中经常应用到归一化处理法,在实践中发挥出重要的应用价值。若输入值在[-1,1]区间外,sigmoid函数的输出响应对输入的敏感性较低。而对输入数据执行归一化处理以后,可以确保数值较大的输入能够分布在sigmoid函数梯度较大的区间内。为了避免在调节权重时造成振荡或超调等问题,输入向量的各个分量最好能够处于同一数量级,而且变化范围适中。在实操中,并未严格要求换算关系,原则上只要能够转换为区间[0,1]内的值,即可达成网络训练效果,而且不易出现分散的结果。
其中,x表示初始数据,x表示经过预处理后的数据;MinValue表示最小的初始样本值,MaxValue表示最大的初始样本值。
在本研究中,选用掘进施工中的第100~119环的20环姿态参数作为样本,并从每一环中选出10个测量点共200个测量点。通过分析这200组数据,得到俯仰角的最大值5.8和最小值0.1,偏航角的最大值5.173'和最小值0.568,滚转角的最大值1.231'和最小值0.097'。为了节省篇幅,以下仅展示了第100环的姿态角数据及其归一化处理后的结果。
前文已述,本文神经网络的输入层、输出层的神经元数量依次是13个和3个,结合以上列出的三个参考公式,针对现实状况,可以估计本文神经网络中隐含层的神经元数量取自于5~15。所以,设定隐含层节点数h的值为5-15的自然数。最佳隐含层神经数量的确定需要不断通过试验检测,在本研究中,隐含层神经元数量为7时,达到了最佳状态。因此,本研究设定隐含层的神經元数量为7。
4预测结果与分析
4.1预测结果
选用第100~119环共20环的姿态参数作为样本,通过网络训练可以得到训练的参数,并在训练结束后建立神经网络模型,并通过该模型对3个姿态角进行预测,所得预测结果依次展示于下图(2)~图(4):
以上图中的实线表示BP神经网络的预测结果,圆点表示实测数据。上图中仅展示了前5环的姿态参数,但是仍然可以窥探出姿态参数的变化规律。
4.2误差分析
根据上述的预测结果,与实际的掘进位置进行比较,得到表4所示的误差分析结果。
根据上表4看出,最大误差是0.0209,如果盾构机在此条件下进行工资,那么直线掘进1000m将会出现5.8mm的位置偏差,说明训练以后的神经网络模型能够较为精准地预测盾构姿态参数。
同时从上述的结果看出,在盾构机向前掘进一个衬砌管片的长度时,盾构机停止掘进,开始拼装衬砌管片,在重启刀盘时,受到地层瞬间作用力的影响,盾构机的滚转角、偏航角及俯仰角瞬时激增。在继续向前掘进的过程中,控制系统会对偏航角、俯仰角进行调节,使得这两项姿态参数有所减小,而滚转角是由反转刀盘进行调节的,所以滚转角是在该环结束以后才开始减小的。上图清晰地展现了盾构机姿态参数在盾构掘进过程中的变化规律,也证实了训练后的神经网络模型可以对盾构机姿态参数进行准确预测。
5结语
神经网络模型能够检验盾构机当前的掘进施工状态是否正常,还能对盾构机在版图中地层条件下的姿态参数进行预测,以预测结果作为依据,操作人员可以快速做出反应,及时调整盾构机掘进姿态,降低掘进过程的偏差,最终保证隧道工程质量。
