人体运动俘能背包的输出功率建模与多参数耦合因素研究
2021-06-10侯泽昊曹军义
侯泽昊 曹军义


摘要: 人?机电耦合俘能背包的输出功率的影响因素复杂,缺乏合理的建模设计方法,因此本文基于机械振动和电路理论建立了人体运动俘能背包的功率输出模型。采用理论模型数值仿真分析了人体负重质量、增速比和行走运动对俘能功率的影响。设计了一种电磁式俘能背包,并搭建了多参数测试系统,实验研究了不同负重质量、运动速度、增速比及其耦合情况下对俘能功率的影响。多参数耦合与阻抗匹配实验结果表明:俘能功率随着负重质量和行走速度的增大而增大,而且在人?机电耦合情况下存在最优增速器增速比和最优外接阻抗使背包输出功率最大。理论和实验结果表明设计的功率输出模型可以为人?机电耦合俘能背包参数设计提供较好的理论指导。
关键词: 俘能背包; 机械振动; 输出功率建模; 多参数耦合因素
中图分类号: TH113.1; TU311.3 文献标志码: A 文章编号: 1004-4523(2021)02-0219-08
DOI:10.16385/j.cnki.issn.1004-4523.2021.02.001
引 言
人体便携式设备功耗通常比较低,如普通聚光手电筒功率约为1.5 W,野战单兵携带的护目夜视镜功耗小于1 W,GPS模块在导航时的功率大约是0.1 W[1]。为了维持这些设备持续工作一定时间,野外工作人员需要携带足够电池。例如野战单兵为了完成72小时野战任务需携带重达7 kg以上的化学电池,占背包总负重的20%左右[2]。这不仅极大降低了野外工作效率,而且限制了人体智能装备进一步发展。同时化学电池还存在容量有限、需要定时更换或充电、废弃电池对环境污染大等棘手问题[3]。而人在日常运动中有大量能量耗散,因此国内外学者开发了各种人体俘能装置收集人体运动耗散能以取代化学电池为便携式设备供电。
人体机械能耗散表现为质心往复、关节旋转和脚底冲击。对应的俘能方式有俘能背包、关节发电机和可发电鞋。Rome等设计了第一款悬挂式俘能背包[4]。Donelan等设计了第一款膝关节俘能器[5]。Krupenkin等利用电湿润法设计出能量俘获鞋[6]。Xie等通过在脚底的齿轮位移放大机构设计了一款能量俘获鞋[7]。Wang等设计了俘获人体腿部摆动能量的装置[8]。可穿戴俘能背包由于其结构紧凑、发电功率大、可靠性高、实用价值突出,引起了学者广泛关注和研究。Yuan等利用机械整流原理设计了一款可以收集人体质心往复双方向运动能量的俘能背包,极大地提高了能量俘获效率[2,9]。为了提高人体舒适性,降低人体额外做功,Mi等提出的俘能背包利用滚珠随着人体质心运动反作用推动丝杠旋转来俘能,同时提出只收集质心向下运动时的能量可以减少人体功耗[10]。Cai等和Liu等分别设计了用于收集人体负功的脚踝俘能器,俘能的同时减少了人体额外做功[11?12]。Xie等提出了一种可改变弹簧刚度的调频俘能背包,使得俘能背包的工作频带变宽[13]。
可穿戴背包与人体相互耦合从而俘能,人体运动状态的变化会对俘能输出产生巨大影响。背包等效动力学模型是单自由度振动模型,所以合理设计背包的负重质量、弹簧刚度和阻尼是高效俘能背包的基础。Rome等的背包实验采用了不同速度和负重,最后在5.6 km/h行走速度和38 kg负重条件下俘获了5.6 W电能[4]。Xie等用两个齿轮齿条机构在5.6 km/h和负重15 kg条件下俘获4.1 W电能[14]。Yuan等发现因为机械整流机构的存在,俘能过程中出现了变阻尼现象,两位实验者在5.6 km/h和负重13.6 kg的相同条件下俘能结果分别为3.3 W和2.1 W[9]。可见不同实验者,不同行走速度,以及不同结构设计即阻尼设计对俘能结果有很大影响。以上分析表明,影响俘能背包输出功率最主要的因素有机电耦合结构、行走速度和负重等。Stephen提出了电磁振动能量俘获系统的理论模型和电路耦合阻尼的分析方法[15]。Tai等在不同激励条件下即不同激励频率和不同外接电阻条件下对电磁振动系统参数进行理论分析,分析了最优设计参数匹配[16]。Yuan等和Xie等在背包设计时进行了详细的动力学建模分析,其模型可以对实验结果做一定预测[9,17]。然而现有理论模型仅仅分析机械阻尼和电阻尼之间的关系,且实验测试不能为进一步设计优化提供参考。为了更好地掌握人体运动俘能背包的动态特性,提高背包的俘能效率,简化背包的设计流程,必须要深入研究不同参数对俘能结果的影响;尤其是输出功率模型,仍需要深入研究不同参数的影响规律。
本文设计了一种人体运动俘能背包,首先以背包动力学设计参数为参量,基于弹簧质量阻尼模型建立了考虑负重质量、增速比和行走运动的俘能功率模型,并对俘能功率模型進行详尽参数分析。采用搭建的实验系统分析了不同实验者、行走速度、运动方式、负重、弹簧刚度、电机选型等多参数对输出功率的影响,得到了人体运动俘能背包功率输出多参数影响规律,为人?机电耦合俘能背包参数设计提供了有力的理论指导。
1 功率输出建模
可穿戴式人体能量俘获背包的主体结构可以等效为一个单自由度弹簧质量阻尼系统,如图1所示。俘能背包的负重作为质量块固定在齿条固定板上与弹簧构成单自由度系统,如图2所示。当人体运动作为位移激励输入俘能背包系统时,俘能背包的负重部分驱动齿条沿着直线导轨上下做往复运动,并利用齿轮齿条机构将往复振动变为旋转运动,然后经由齿轮箱放大从而驱动电机发电。根据机械振动知识,环境能量通过阻尼流入俘能系统内
P_ave=1/2 cω^2 A_0^2 (1)
式中 P_ave为流入系统的平均功率,c为总阻尼,ω为激励频率,A_0为阻尼两端的相对位移。在总阻尼中机械阻尼仅仅消耗了环境能量发热或产生噪声,而电路等效阻尼将环境能量转化为电能供外接电路用电器使用。且人在行走过程中双腿交替前进的结果是质心的上下振动,这相当于给俘能结构输入一个近似简谐的位移激励。所以可穿戴式人体能量俘获背包的运动可以简化为一个单自由度弹簧质量阻尼系统在简谐位移激励下做受迫振动,可穿戴式人体能量俘获背包的俘能功率是阻尼的耗能功率。对于一个俘能系统而言,能量通过阻尼从外界环境流入俘能系统之内,如式(1)所示,而只有外接电路等效阻尼俘获的能量做有用功,其余能量都转化为热能耗散。
故用简谐位移激励下相对位移表达式替换式(1)中的A_0,俘能背包的模型如下式所示
P_ave=1/2 c_R ω^2 (m^2 〖X_0〗^2 ω^4)/((k-ω^2 m)^2+(c_m+c_r+c_R )^2 ω^2 ) (2)
式中 P_ave为俘获的能量;c_R为外接电路等效阻尼;m为负重质量;X_0为激励位移;k为悬挂弹簧刚度;c_m为机械阻尼;c_r为内阻等效阻尼。为了方便分析俘能背包俘能功率,假设外接电路用电器是一个纯电阻R,根据文献[15]所述,等效电阻尼与外阻R和内阻r相关。
圖3(a)是电机电路等效图,图3(b)是负重端受力分析图。图中N为齿轮箱增速比,r_d为齿轮啮合半径,K为电机反电动势系数,x ˙为背包的绝对速度,x ˙_0为人体的绝对速度。考虑俘能装置旋转半径和齿轮箱作用,相对输入线速度从齿轮端经过齿轮箱放大N倍传递到电机端,则电机端角速度为(N(x ˙-x ˙_0))/r_d ,在图3(a)电机电路图中电机发电电压为(NK(x ˙-x ˙_0))/r_d 。同理电机反电动势阻力矩经齿轮箱放大N倍传递到输入端,则输入端阻力大小为KNi/r_d 。根据图3(a)的电路基尔霍夫定律和图3(b)的受力分析可得下式
消除式(3)中的i,可得系统动力学方程
式(4)中由外阻R和内阻r产生的电阻尼为
c_r+c_R=(N^2 K^2)/((R+r)r_d^2 ) (5)
根据全电阻电路的欧姆定律,可得外接电路阻尼为
c_R=(RN^2 K^2)/(〖(R+r)〗^2 r_d^2 ) (6)
由于电机转速较低[11],可忽略电机的感抗作用。将式(6)代入式(1)中,并做近似无量纲处理,即分子分母同时除以2ω_n m
式中 ω_n为系统固有频率;α为激励频率比;ξ_m为机械阻尼比。考虑到齿轮箱对电机机械阻尼的放大作用,系统机械阻尼可以表示为结构机械阻尼和电机机械阻尼的和。假设齿轮箱阻尼不随增速比变化,且电机阻尼以线性关系放大到输入端,机械阻尼可以表示为
c_m=c_0+Nc_1 (8)
式中 c_0为结构机械阻尼;c_1为电机机械阻尼。故而式(7)可以表示为
2 理论数值分析
实验表明不同人在不同速度下正常行走的速度范围为4?5.6 km/h,行走频率在2±0.02 Hz附近,行走速度快慢主要由步幅决定,并不是步频决定。所以理论数值分析中,激励频率选择为2 Hz。对于同一个人以不同的速度正常行走,只是步长的变化,表现为重心上下振动的幅度不同,即激励振幅的变化。对于不同人以相同速度行走,因为人身高腿长的差异,造成其重心上下振动的幅度不同,也表现为激励振幅变化。激励振幅在式(9)中以X_0^2出现,随着行走速度增大,X_0增大,输出电压显然升高。其他仿真参数选择:内阻为2 Ω,弹簧刚度为3000 N/m,反电动势系数为0.005 V/(r/min),旋转半径为0.015 m,结构机械阻尼为8 N?s/m,电机机械阻尼为3 N?s/m。根据式(9),数值仿真分析负重质量、增速比及外接电阻对俘能效果的影响。
图4和图5描述了负重质量对输出电压影响的理论分析结果。图4的仿真条件是增速比N为25,外接电阻R为50 Ω,图中的三条仿真曲线分别表示仿真在三种不同激励位移条件,即X_0为0.01,0.015,0.02 m条件下进行。激励位移X_0选择0.015 m,外接电阻R为50 Ω,得到的仿真结果如图5所示,图中的三条仿真曲线是分别选择三种不同增速比N为22.5,25,30得到的。为了与后文实验结果比较,对负重质量m从8.2 kg至10.2 kg区域放大。从图中可以看出,随着负重增加,输出电压出现极大值点,继续增大负重,输出电压有下降趋势,但整体趋于平缓,在质量变化范围不大时可以近似认为输出电压随着质量线性增长。同时,由图4可知,当增速比不变时,激励位移越大输出电压越高。由图5可知,当激励位移不变时,随着质量增加,三种不同增速比对应的输出电压曲线相交。于是得出结论:激励位移越大,输出电压越高;随着质量变化,增速比的影响规律也会随之变化。
为了分析增速比的影响,仿真分析了在激励位移X_0为0.02 m,外接电阻R为50 Ω情况下,输出电压与增速比的关系,理论仿真结果如图6所示。图中的三条仿真曲线分别表示三种不同负重质量m为8.2,9.2,10.2 kg下的输出电压与增速比的关系。为了与后文实验结果比较,对增速比N从22.5至30区域放大。从图6中可以看出随着增速比增大,输出电压也有极值点出现;增速比继续增大时,输出电压开始下降。由式(5)和(8)可知,增速比N影响着系统的电阻尼c_r+c_R和机械阻尼c_e的大小,所以在式(9)中,随着增速比N增大,总阻尼c增大,从而输出电压出现下降趋势。
为了分析输出功率随外接负载的变化规律,理论仿真分析了不同负重情况下俘能背包的输出功率随阻抗的变化关系。图7的阻抗匹配分析是在激励位移X_0为0.015 m,增速比N为25条件下进行,其中的三条仿真曲线代表着三种不同负重质量m为8.2,9.2,10.2 kg。从仿真结果可以看出,随着阻抗增大有最优外接阻抗存在,在当前仿真参数设置条件下,最优外接电阻约为50 Ω。
3 实验验证研究
3.1 实验系统描述
实验设计了基于机械整流的可穿戴式人体能量俘获背包,具体的俘能背包和测量传感单元如图8所示。图8中的位移传感器(Panasonic, HL?G112?A?C5)测量固定板和载荷背包之间的相对位移,加速度传感器(MEMSIC,CXL10GP3)测量人在行走过程中质心的加速度。为测量分析俘能背包的输出功率,电阻箱作为外接可变负载接入电磁发电机的输出端,同时安捷伦存储示波器(Agilent,MSOX3052A)并联在电阻箱两端测量外接电阻两端的端电压,由此可以计算人体运动过程中的实时输出功率。
实验时,首先打开直流稳压源给传感器供电,然后在背包中装入重物使背包有一个初始偏移。要求实验者背负背包在跑步机(T32)上运动至少30 s,等待运动平稳后开始测量数据,每一组至少测量三组数据,采样时间为20 s,采样频率为100 Hz。当实验者开始运动时,实验者质心会随着双腿前后交替而上下往复运动,俘能背包在质心的位移激励下开始做受迫振动。图2是俘能背包俘能结构示意图,当俘能背包做往复受迫振动时,齿条齿轮机构将直线运动变为旋转运动经由齿轮箱输入电机发电。此时,加速度传感器测量人体质心上下振动的加速度,激光位移传感器测量固定板和载荷背包的相对位移。为了保证测量的同步性,加速度信号、位移信号和电压信号都使用同一个示波器测量,图9是实验系统详细连接框图。
3.2 多参数影响实验
实验中首先控制外接电阻为50 Ω,研究负重质量、行走速度和增速比等参数对俘能结果的影响。图10给出了在增速比为22.5和负重为8.2 kg时,输出电压随着行走速度的变化情况。实验结果表明:随着行走速度加快,输出电压增大,即输出功率增大;图中三条曲线代表不同实验者,表1给出了参与实验的三位实验者的身高、体重和年龄。实验者1在行走速度从4.6 km/h增加到5.6 km/h时,其背包输出的电压从1.5 V增加到5.4 V。而实验者2和3的相应输出电压变化没有实验者1变化的大,可以看出人?机电耦合的俘能背包输出影响因素较为复杂。不过也可从图中看出,不同实验者会影响输出功率的大小但不影响输出的趋势变化。图11给出了实验者1在行走5 km/h时输出电压随着增速比的变化情况。图10和图11与第2节中图4和图6趋势相同,实验结果与理论推导结果具有一致性。值得注意的是,在图11中实验者1负重8.2 kg時曲线出现了拐点,说明增速比和负重有一定关联。第2节中图5中三种不同增速比曲线在质量增大时出现交点,这与实验结果可以相互验证。但是在理论分析中,没有考虑到电机转动惯量的影响,而增速比的变化会使电机惯量的等效质量发生变化,引起系统固有频率的偏移。
图12研究了实验者2在增速比为25条件下,输出电压随着负重质量的变化情况。因为负重质量与背包振动行程密切相关,所以根据实验背包设计的负重范围,考虑到实验结构的行程限制,仅仅选取质量为8.2,9.2和10.2 kg进行实验。图12实验结果表明,随着负重增加,输出电压升高。这与理论分析图4和5结果相同,但是在图12中行走速度5.6 km/h条件下曲线斜率出现变化。因为随着负重增加,人体的自身自适应调节倾向于减小步幅。所以负重继续增加且速度不减的同时人体倾向于加快步频缩短步幅,从而导致输出位移趋于平缓,这一点并没有在模型中反映出来。图13分析了实验者3在速度5.6 km/h时,输出电压随着负重的变化情况。图13实验结果与图12实验结果相同,即输出电压随着负重增加而增加,且不同增速比对实验结果影响不大。但是在负重10.2 kg条件下,增速比的影响趋势与8.2 kg和9.2 kg影响趋势完全不一致。与图5中三种不同增速比曲线在质量增大时出现交点,图11负重8.2 kg时有拐点的结论相互印证,这说明增速比的影响趋势与质量有一定关系。
与此同时,实验结果与理论结果的坐标数量级相同,但是数值相差较大,实验结果普遍偏高。因为理论模型中是基于单自由度弹簧质量系统建模,而实际实验时背包中加入了机械整流器,所以理论和实验结果存在一定的误差,机械整流器会提高俘能效率。但是其基本趋势一致,理论结果并不影响趋势判断和参数选型。在理论分析中,电机阻尼参数是根据经验选择的,且假定齿轮箱阻尼与增速比为线性关系,这也给理论分析带入一定误差。
3.3 电机影响实验
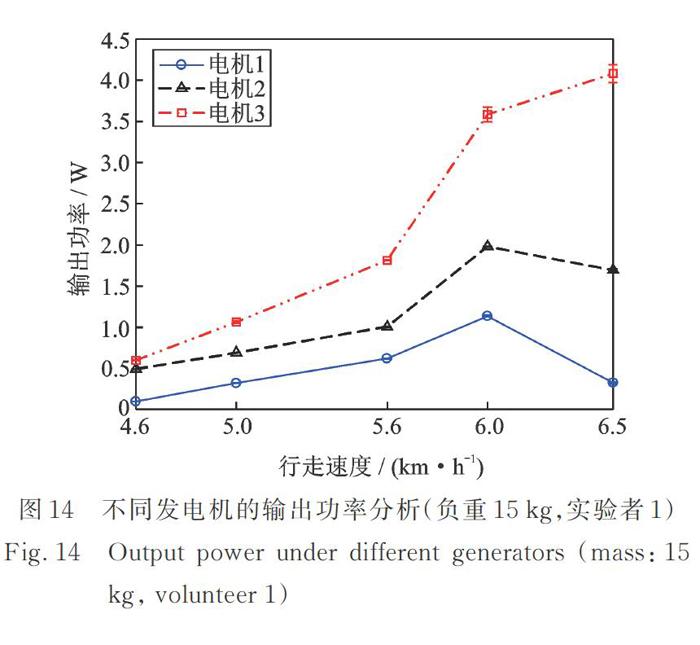
式(9)中体现电机参数的有反电动势系数K,电机机械阻尼和内阻r,所以电机选型会对俘能背包的俘能功率产生很大的影响,故进一步进行了不同电机对俘能结果的影响实验,表2给出了不同测试电机的参数。实验者1在负重15 kg,外接电阻50 Ω条件下连续变换速度运动。首先以4.6,5和5.6 km/h行走;然后以6和6.5 km/h跑步。图14中三台电机的三条曲线在行走5.6 km/h和跑步6 km/h之间斜率发生了很大变化,因为跑步时存在双脚离地状态,故而人体不再是一个简单的简谐运动,而有冲击信号作用在俘能背包上,使得俘能功率急剧上升。然而电机1和电机2在跑步速度为6.5 km/h时,发电功率下降。主要因为背包结构限制,当跑步过快出振幅超出行程,俘能背包相对位移太大与框架撞击,损耗了大部分能量。
3.4 负载特性实验
最后选择电机3,让实验者1运动在负重15 kg,速度5.6 km/h条件下,研究外接负载对输出功率的影响。实验中外接电阻以5 Ω为步长,从5 Ω开始连续变化到150 Ω,从图15中可以看到在50 Ω附近有一个明显的拐点存在,与理论模型分析图7相符,验证了输出功率模型的有效性。
4 结 论
本文基于可穿戴式人体能量俘获背包建立了俘能功率模型,并进行了详细的多参数理论和实验分析,从理论和实验角度分别分析了行走速度、运动方式、负重质量、增速比以及不同实验者对俘能功率的影响。具体结论如下:
1)输出功率与负重质量、运动速度成正比;
2)输出功率与齿轮箱增速比存在一个最优匹配,不同电机有不同的最优增速比;电机的不同会影响俘能背包的运动状态和发电功率;
3)实验者对输出效率有一定的影响,但是不影响多参数分析的实验规律;
4)跑步状态比行走状态的发电效率好,其主要原因是跑步时频率提高;其次是因为跑步时有腾空过程,双脚交替时的冲击作用提高了输入能量。
5)弹簧刚度对发电功率影响较小,在刚度相同情况下,质量越大俘能效果越好。
参考文献:
[1] Choi Y M, Lee M, Jeon Y. Wearable biomechanical energy harvesting technologies[J]. Energies, 2017,10(10):1483.
[2] Yuan Y, Liu M Y, Tai W C, et al. Design and experimental studies of an energy harvesting backpack with mechanical motion rectification[C]. Proceedings of SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Portland, Oregon, United States, 2017.
[3] Wei C, Jing X. A comprehensive review on vibration energy harvesting: Modelling and realization[J]. Renewable & Sustainable Energy Reviews, 2017, 74:1-18.
[4] Rome L C, Flynn L, Goldman E M, et al. Generating electricity while walking with loads[J]. Science, 2005,309(5741):1725-1728.
[5] Donelan J M, Li Q, Naing V, et al. Biomechanical energy harvesting: Generating electricity during walking with minimal user effort[J]. Science, 2008, 319(5864):807-810.
[6] Krupenkin T, Taylor J A, Mattioli V, et al. Sole for footwears capable of recovering part of the energy produced during deambulation[P]. US Patent: IB2015/050777, 2015.
[7] Xie L, Cai M. An in-shoe harvester with motion magnification for scavenging energy from human foot strike[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(6):3264-3268.
[8] Wang W, Cao J, Zhang N, et al. Magnetic-spring based energy harvesting from human motions: Design, modeling and experiments[J]. Energy Conversion and Management, 2017,132:189-197.
[9] Yuan Y, Liu M, Tai W, et al. Design and treadmill test of a broadband energy harvesting backpack with a mechanical motion rectifier[J]. Journal of Mechanical Design, 2018,140: 0850018.
[10] Mi J, Xu L, Zhu Z H, et al. Design, modeling and testing of a one-way energy harvesting backpack[C]. Proceedings of SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Denver, Colorado, United States, 2018.
[11] Cai M, Liao W, Cao J. A smart harvester for capturing energy from human ankle dorsiflexion with reduced user effort[J]. Smart Materials and Structures, 2019, 28(1): 0150261.
[12] Liu M Y, Tai W C, Zuo L. Energy harvesting from ankle: Generating electricity by harvesting negative work[C]. Proceedings of the ASME Conference on Smart Materials Adaptive, 2018.
[13] Xie L, Cai M. Increased energy harvesting and reduced accelerative load for backpacks via frequency tuning[J]. Mechanical Systems and Signal Processing, 2015, 58-59: 399-415.
[14] Xie L, Cai M. Development of a suspended backpack for harvesting biomechanical energy[J]. Journal of Mechanical Design, 2015,137: 0545035.
[15] Stephen N G. On energy harvesting from ambient vibration[J]. Journal of Sound and Vibration, 2006, 293(1-2): 409-425.
[16] Tai W, Zuo L. On optimization of energy harvesting from base-excited vibration[J]. Journal of Sound and Vibration, 2017, 411: 47-59.
[17] Xie L, Li X, Cai S, et al. Increased energy harvesting from backpack to serve as self-sustainable power source via a tube-like harvester[J]. Mechanical Systems and Signal Processing, 2017, 96: 215-225.
Output power model and multi-parameter coupling effect of a wearable energy harvesting backpack
HOU Ze-hao, CAO Jun-yi
(Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System,
Xi'an Jiaotong University, Xi'an 710049, China)
Abstract: Due to complex effects of different human-electromechanical coupling parameters, theoretical models and design of output power of wearable energy harvesting backpacks remain uninvestigated. In this paper, the captured power model of a wearable energy harvesting backpack is established based on engineering vibration and circuit theory. Based on the proposed model, the influence of load mass, gearbox ratio and walking motion on the captured power is numerically analyzed. The multi-parameter experimental system based on the proposed electromagnetic energy harvesting backpack is built to study the relationship between weight, speed, gearbox ratio and the captured power. Experimental results show that weight and speed are positively correlated with the captured power. The gearbox ratio and external resistance have optimal values to maximize the output power performance of an energy harvesting backpack. It is also demonstrated that the proposed power output model can provide good theoretical guidance for designing optimal parameters of the wearable energy harvesting backpack.
Key words: energy harvesting backpack; mechanical vibration; output power model; multi-parameter coupling effect
作者簡介: 侯泽昊(1995-),男,博士研究生。电话:15029353101; E-mail: xiaohou205@126.com
通讯作者: 曹军义(1977-),男,教授。电话:(029)82667938; E-mail: caojy@mail.xjtu.edu.cn
