地下空间结构多车作用下耦合振动研究

林延城

摘要：文章主要将地下空间结构悬浮隧道作为研究对象，分析多车作用下的车隧耦合振动。首先建立多车辆和隧道耦合振动数学模型，由于悬浮隧道与两岸连接，于是文中将其假设为简支梁结构。然后研究了车辆速度、车辆质量、车辆之间的间距对隧道响应的影响。结果表明，车辆的间距和车辆速度对悬浮隧道的动态响应比较大，车辆质量对悬浮隧道的动力放大系数影响会随着车速的不同而不同。

关键词：多车作用;耦合振动;悬浮隧道

中图分类号：U441⁺.3 文献标识码：A 文章编号：1001—5922（2021）02-0171—04

地下空间结构常见的有隧道、地下停车场等，文章将主要研究隧道中的悬浮隧道，然后分析其车隧耦合振动。悬浮隧道属于一种悬浮在水下的一种新型封闭式交通结构物。作为一种新形势跨江海域交通方案，得到了国内外学者的重点关注。悬浮隧道主要由3部分组成，分别为隧道管体、锚固装置和驳岸段。该隧道主要依靠锚索的张力使得自身保持平衡。因其处于水下，长年会受到车辆荷载和洋流的影响，所以悬浮隧道需要具有非常好的性能。很多学者对洋流和悬浮隧道之间的作用进行分析，也有很多学者对锚索和隧道之间的关系进行分析，推到了各种不同方程。这些研究使得我们能够更好的认识到悬浮隧道的受力特点。还有学者研究了车辆荷载对隧道的动力响应影响，将悬浮隧道等价为弹性支撑梁结构，然后分析了等间距对隧道管体的位移响应。这些研究中很少涉及到多车辆和隧道之间的耦合振动作用。于是文章在前人研究的成果上，对多车辆作用下隧道耦合振动分析。

1理论分析模型

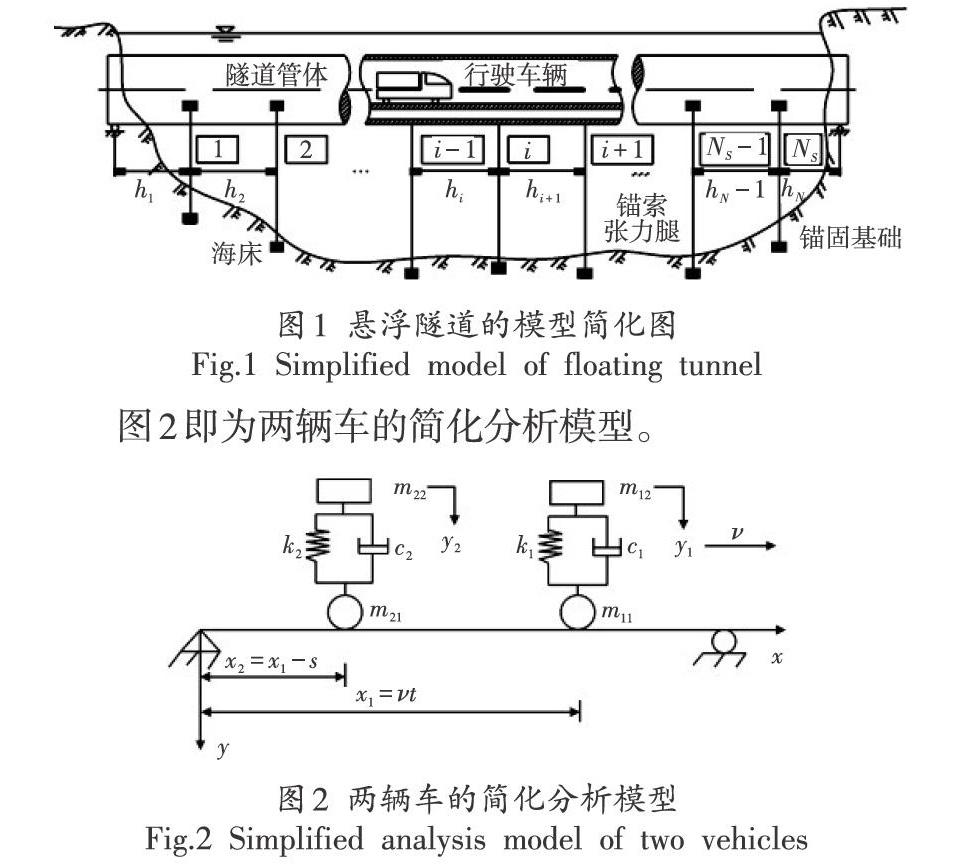
图1即为地下空间结构悬浮隧道的简化模型图，其中锚索张力腿在静水情况下只存在竖向的刚度Ki（i=1，2，…，Ns），因为水平方向的力通过两侧对称的锚索分力自平衡抵消。锚索之间的距离使用hi（i=1，2，…，Ns）进行表示。为了研究多车作用下车隧耦合振动，需要做以下假设：①设隧道处于静水环境下，即张力腿只会受到竖直方向的约束力;②由于悬浮隧道和海岸量孤单相连接，于是将其看做为简支边界条件，将该隧道整体上视为梁;③将行驶车辆简化为单自由度的弹簧一质量车。

文章研究的是地下空间结构多车作用下的耦合振动，于是需要建立M辆车的车隧耦合振动控制方程，一共包含M+1个方程组。其中第M个方程和第M+1个方程组属于隧道控制方程，其他的属于车辆控制方程：

其中N为隧道模态阶数，yi为第i辆车竖向位移，t为车辆运行时间，E为弹性模量，E、u和1分别表示的是隧道弹性模量、线密度和惯性矩，ci为车辆阻尼系数，ki为车辆刚度，v表示速度，Pi=（mn1+mi2），Yi为隧道的第i个模态位移，s为车辆间距，c为隧道阻尼系数，δ（x1为狄拉克函数，y（x，t）为t时刻x处隧道竖向位移。

2结果分析

2.1车辆速度的影响

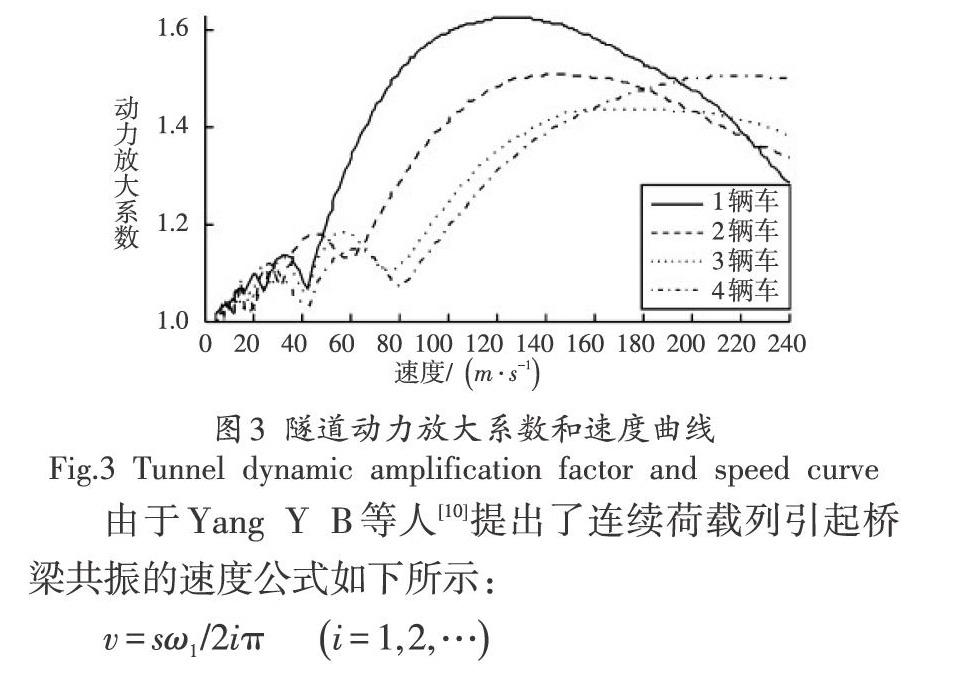
将车辆速度从4m/s变换到240m/s进行分析，并且假定车辆之间的间距相等，即s=8m，然后通过计算模型，得到动力放大系数的结果如图3所示。从图中可以看出，当车辆数量不同时，动力放大系数曲线（DAL）存在明显的区别，且当车辆数量越多时，车速度保持不变，动力放大系数将会越来越小，即可说明，当车辆变多时，最大静态位移增长的速度大于最大动态位移增长的速度，所以在对地下空间结构悬浮隧道进行研究设计时，需要更多的考虑一车和动力放大系数之间的差异。从图中还可以看出，当车辆速度保持不变时，当车辆速度越来越大，动力放大系数也会有增长的趋势。

其中ω1，表示的是桥梁第一自然圆频率。图4为3～6辆车，且间距为26m的动力放大系数的对比，虽然该文章分析的是桥梁，但是本文所研究的悬浮隧道同样将其简化为桥梁形式。从图中可以看出，车辆数量不同时动力放大系数曲线相位几乎保持一致，只是在局部峰值范围内存在一点差异，出现这种现象是因为当车辆数量越多时，隧道振动的时程将会延长，继而增加了峰值，所以在峰值出存在差异。表1为共振速度和动力放大系数值，其中一共计算了2～7辆车的系数，且该表中的车辆间距为26m。从表中可以看出，当车辆不断增加时，局部峰值对应的速度与Yang Y B等人中计算的共振速度越来越接近，但是当车辆为7时，峰值对应的速度不再发生变化。在实际情况中，接近局部峰值的速度同样具有共振效应，所以设计师对隧道进行设计时，还需要注意在峰值附近的速度所产生的位移放大效应。

2.2车辆间距的影响

将车辆速度保持定值，然后分析车辆间距不同时对隧道动态响应的影响，将车辆间距的范围设置在0.5～29.5m之间，然后每次增加0.5m。并且分析3个车辆速度下的车辆间距对隧道动态响应的影响，速度分别为20m/s、60m/s、100m/s。在进行实验过程中，选择跨中最大动态位移进行观察，结果如图5所示。从图中可以看出，当车辆间距不断增加时，跨中位移的变化趋势没有呈现出单调變化趋势，当车辆速度为20m/s时，且车辆间距小于19m时，跨中位移整体上呈现出下降的趋势，然后当间距大于19m之后，跨中最大位移发生了非常明显的降低趋势，且达到了一个最小值。当车辆速度为60m/s时，跨中最大位移是当车辆间距处于19-24m之间时达到明显的降低趋势。当车辆速度为100m/s时，跨中最大位移是当车辆间距处于16～22m之间时达到明显的降低趋势。通过计算间距和隧道跨比之后，发现不同车辆速度时，跨中位移发生明显的降低趋势是当间距和跨比为0.6时。于是可以通过使用该结论合理设计车辆间距或者隧道跨度。

通过E述分析，不同的车辆速度和间距对隧道动态相应的影响可以绘制出如图6所示的云图，其中显示的是跨中最大动态位移的变化规律，从图中可以同时观察特定速度或者特定间距保持不变时，其中另外一个因素对跨中位移的影响。可以观察到图6的3幅图中，隧道跨中位移的变化规律大致相同，比如每幅图的左上角跨中位移呈现出比较小的特定，此时的车辆间距大于15m，速度小于40m/s。通过观察云图，可以得出结论为车辆间距越小、速度越大，隧道跨中响应就会越大。除了车辆速度在90—110m/s时，不会呈现出此规律，即当车辆间距靠近隧道跨中时，其中动态位移还是相当大。

2.3车辆质量变化的影响

车辆质量的变化可以从两个方面进行分析，其中一种就是车辆的总质量和隧道质量比，另外一种就是轮胎和悬架之间的质量比。这两种方式都能够表示出车辆质量的变化。其中保持悬架质量不变，然后使得车辆轮胎的质量发生变化，然后将轮胎和悬架的质量比设置在0%-15%之间。且将车辆间距设置为10m，车辆速度设置为20m/s、60m/s、100m/s，然后分析质量比不同时，动力放大系数的变化趋势，结果如图7所示。从图中可以看出，在这3种速度之下，轮胎和悬架之间的质量比发生变化时，动力放大系数的变化不大，只有稍微一点变化，即变幅非常下，所以车辆轮胎对隧道的动力放大系数影响非常小。

然后再分析车辆总质量和隧道质量比不同的情况下，隧道动力放大系数的变化趋势。将车辆总质量和隧道质量比设置在0.2%-15%之间，那么当隧道上有两辆车时，车辆质量和隧道质量的变化范围增加了一倍，即0.4%-30%。同样分析3种不同车辆速度情况下，质量比对动力放大系数的影响。结果如图8所示。从图中可以看出，当车辆速度存在差别时，质量比对动力放大系数的影响程度也不—样，即动力放大系数的变化没有呈现出单调的变化趋势。于是在不同速度之下，动力放大系数达到最大值和最小值时对应的质量比如表2所示。

3结语

综上所述，分析不同车辆情况下车隧耦合振动。从结论可知车辆速度对地下空间结构悬浮隧道的动态响应比较大，隧道中不管存在多少辆车，其移动荷载都会影响隧道发生共振效应，从其结论可知响应峰值所对应的速度及其附近位移最大效应都会非常的注意。另外，车辆间距对悬浮隧道动态响应也比较大。当车辆间距和隧道比值在0.6左右时，隧道的响应最小，所以设计者可以参考该数值对隧道进行设计。车辆质量在一定程度上也会对隧道动力放大系数造成影响，但是从其结果看来，车辆轮胎和悬架质量比对动力放大系数的影响非常小，只有车辆总质量和隧道质量比对动力放大系数的影响比较明显，且当车辆速度不同，质量比对最大放大系数的影响程度也会存在较大差异。