圆筒型反向式横向磁通直线电机定位力补偿二阶自抗扰控制器位置控制
2021-06-10董顶峰黄文新卜飞飞黄维康
董顶峰 黄文新 卜飞飞 黄维康 姜 文
圆筒型反向式横向磁通直线电机定位力补偿二阶自抗扰控制器位置控制
董顶峰1,2黄文新2卜飞飞2黄维康2姜 文2
(1. 南京埃斯顿自动化股份有限公司 南京 211106 2. 南京航空航天大学自动化学院 南京 211106)
为减小定位力、摩擦力及负载等扰动对圆筒型反向式横向磁通直线电机(TRTFLM)位置控制性能的影响,提出一种定位力补偿二阶自抗扰控制器(ADRC)。首先,给出该电机的基本结构与运行原理,并对其定位力产生机理、数学模型及谐波分量进行分析;其次,基于该电机的数学模型,将位置环与速度环进行并联设计,构建位置环二阶ADRC,提高了TRTFLM位置控制的抗扰性能及跟踪性能;在此基础上,将定位力模型嵌入至扩张状态观测器(ESO)中,实现对二阶ADRC的优化,进一步提高了位置控制跟踪性能;最后,实验表明该控制方案的可行性和有效性。
圆筒型反向式横向磁通直线电机 定位力 自抗扰控制 位置控制
0 引言
圆筒型反向式横向磁通直线电机(Tubular Reversal Transverse Flux Linear Machine, TRTFLM)不仅具有传统圆筒型横向磁通直线电机不存在横向边端效应、不存在单边磁拉力及推力密度高的优点,而且具有圆筒型磁通反向式直线电机初级制造工艺简单及圆筒型开关磁阻直线电机次级结构简单、可靠性高、成本低等优点,应用于长冲程场合具有独特的优势[1-3]。然而,该新型结构电机仍属于直驱电机,其动子与负载直接相连,定位力、摩擦力及负载等扰动因素直接作用于电机本体,是一种典型的多变量、强耦合、时变的非线性控制对象,因此经典的PID控制难以满足高性能位置控制的要求,使其应用范围受限[4-6]。为了提高TRTFLM位置控制的抗扰能力、跟踪性能,并进一步抑制定位力的影响,对该电机设计出一种定位力补偿二阶自抗扰控制器(Active Disturbance Rejection Control, ADRC)的位置闭环控制系统。
ADRC是由韩京清研究员提出的一种非线性控制算法,其统一处理内外扰动的思想在多个应用领域取得了丰硕成果[7-10]。其中,在电机位置控制方面,可以提高其跟踪性能及抗扰能力,已有许多学者进行了相关研究。文献[11]将ADRC应用至永磁同步电机位置环控制中,实现对其位置的精密运动控制,取得了显著的效果。为了克服系统响应速度和超调之间的矛盾,同时提高系统的抗扰能力,文献[12]将传统的三环位置控制系统改造为双环结构,即位置环和电流环,提出了一种二阶ADRC,并将其应用至位置伺服系统中。基于文献[12],文献[5]将模糊控制原理应用到ADRC中,提出了一种模糊ADRC,在保证系统跟踪性能的同时,进一步提高了位置控制系统的抗负载扰动的能力。为解决位置环采用常规二阶ADRC的永磁同步电机伺服系统中速度不可控的问题,基于滑模控制的一体化设计思想,文献[6]提出了一种位置、速度控制器一体化设计方法。该方法采用偏差反馈的算法对转速进行限幅,实现了四段式位置伺服控制。文献[13]提出了一种位置电流双环的自抗扰控制结构,给出了位置的二阶非线性ADRC和q轴电流的一阶线性ADRC的设计方法,研究表明该方法对负载转矩、电机参数变化等扰动具有较好的抑制作用。
本文在文献[12]的基础上,借鉴文献[14]基于模型补偿ADRC的思想,提出了一种定位力补偿二阶ADRC。文中首先给出了该新型电机拓扑的基本结构,并对其定位力进行了详细分析;随后将二阶ADRC引入到TRTFLM位置控制中,提高了该电机位置控制的抗扰性能及跟踪性能,同时基于定位力模型,实现对二阶ADRC的优化,进一步改善了位置跟踪性能;最后实验验证了所提方法的可行性和有效性。
1 电机结构与运行原理
1.1 电机结构
3相4极12槽TRTFLM拓扑结构示意图如图1所示,包括初级、次级、初级铁心单元及单元电机铁心。

图1 电机结构
初级由初级铁心单元、电枢绕组及永磁体组成。初级铁心由6个单元电机铁心组成。单元电机铁心由4个初级铁心单元沿轴向依次翻转180°叠压而成,此时单元电机铁心齿在轴向呈长齿、短齿交替式分布。初级铁心单元的齿部和轭部由硅钢片一次叠压而成,生产工艺简单。电枢绕组与旋转电机集中绕组结构相同,线圈绕制和嵌线工艺简单易实现,且三相绕组在周向呈现U、V、W、U、V、W式分布。N极永磁体安装在初级铁心单元的短齿内圆面上,由于单元电机铁心齿在轴向呈长齿、短齿交替式分布,使得N极永磁体在相邻初级铁心单元内产生两个方向相反的磁通,因此,该电机具有磁通反向式电机特点[15]。多个硅钢片叠压而成的次级铁心单元在轴向及周向错位分布,构成次级。次级铁心单元外圆面轴向中心线处有凹槽,凹槽和初级铁心单元的槽口对齐,使两者之间产生一定的周向力,从而限制两者之间的相对周向运动。每列轴向错位分布的次级铁心单元分别对应一个初级铁心单元,加上初级铁心单元上的线圈及永磁体,共同构成一个单元电机,周向互差180°机械角度的两个单元电机构成一相。该电机的设计参数见表1。
表1 电机参数

Tab.1 Parameters of machine
1.2 运行原理
图2给出了该电机结构展开图。如图2所示,U相由两组线圈U1、U2组成,V相由两组线圈V1、V2组成,W相由两组线圈W1、W2组成。其中,U1、V1、W1分别代表每相线圈顺时针缠绕,U2、V2、W2分别代表每相线圈逆时针缠绕,每相相邻两个线圈之间串联,每相两组线圈之间串联。永磁体长度为,即为该电机极距,轴向呈现单N极交替式分布,周向呈现双N极交替式分布,并且此时周向相邻初级铁心单元之间磁路彼此相互独立。次级由2组次级铁心单元组成,每组内的3列次级铁心单元沿周向依次对应U、V、W三相,3列次级铁心单元的轴向中心线依次间距2/3,每列相邻次级铁心单元的轴向中心线之间间距2。
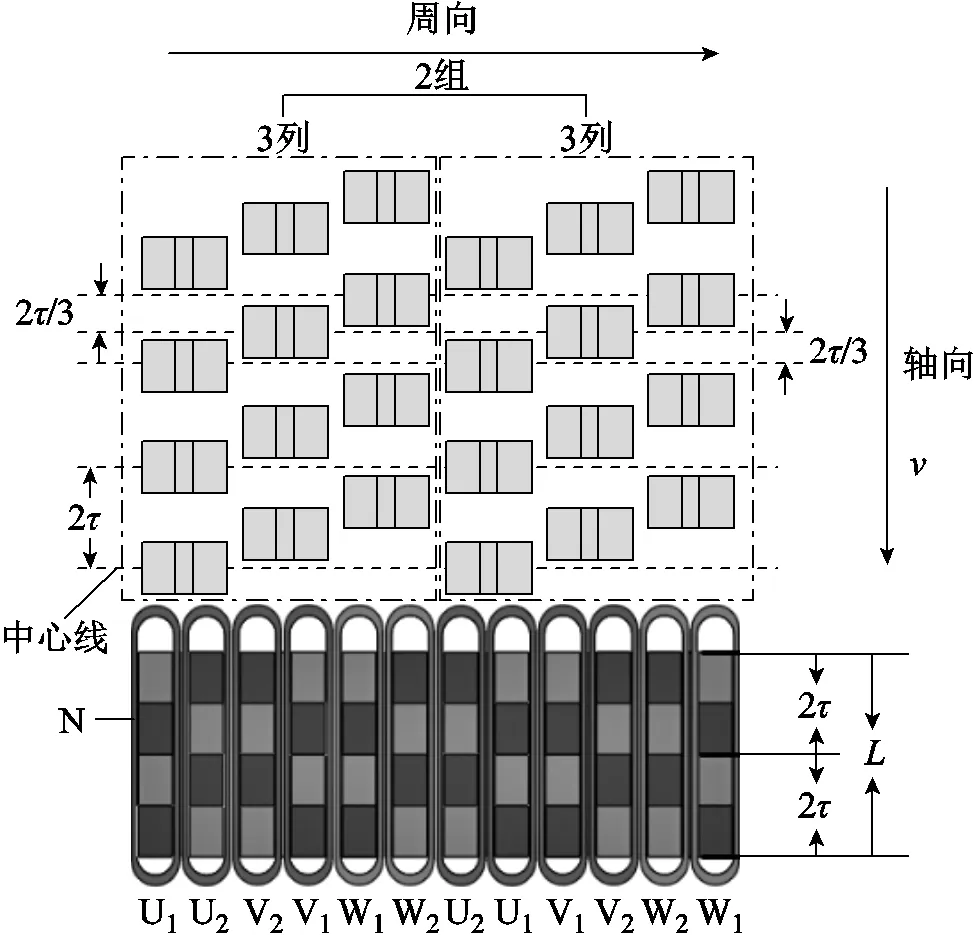
图2 电机结构展开图
当次级以速度沿轴向移动时,由于永磁体单N极轴向交替式分布的原因,将在单元电机铁心内部产生和运动方向垂直的交变磁通,即横向磁通电机特点[16]。相磁通交变路径如图3所示,图3给出了U相两个典型位置磁通路径的示意图,当次级铁心单元的轴向中心线和线圈U2对应的永磁体的轴向中心线对齐时,磁通达到最大值,且方向为逆时针,如图3a所示。而当次级铁心单元的轴向中心线和线圈U1对应的永磁体的轴向中心线对齐时,磁通达到最大值,方向为顺时针,如图3b所示,磁通实现交变。由于每相对应的次级铁心单元的轴向中心线之间依次间距为2/3,则在其对应的三相绕组中将产生对称且互差120°电角度的三相反电动势,其频率为=/(2)。当三相对称绕组被通入三相幅值相同、相位互差120°的交流电时,基于磁阻最小原理,初级与次级相互作用,若固定初级,则次级将沿直线方向移动。
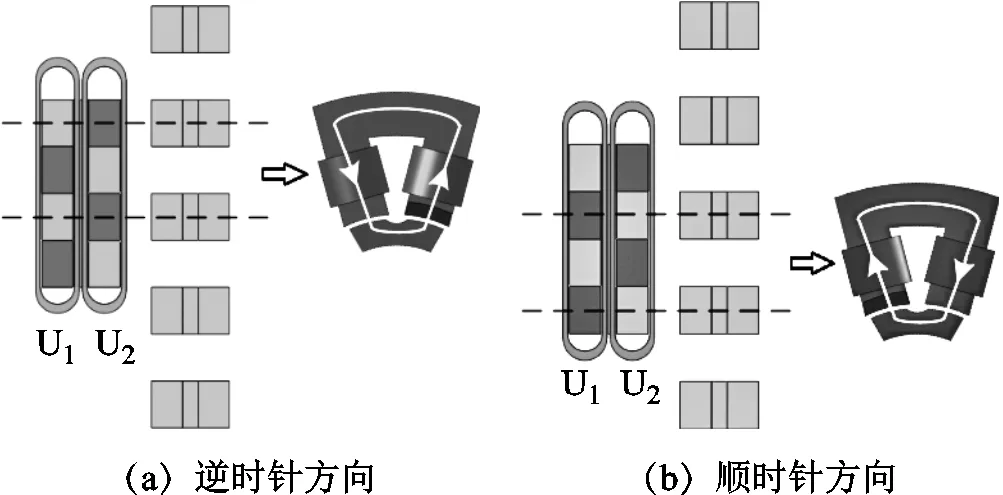
图3 相磁通交变路径
2 定位力分析
定位力是影响该电机位置控制性能的重要因素之一,主要包括齿槽定位力和端部定位力。对于该电机,其齿槽定位力是由初级永磁体和次级铁心齿槽结构相互作用而产生。根据文献[16],单元电机齿槽定位力的傅里叶表达式为
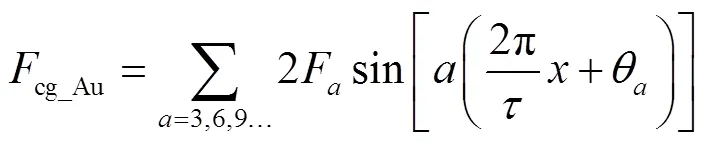
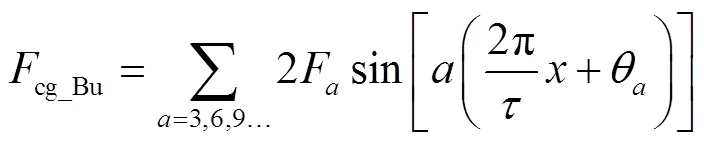
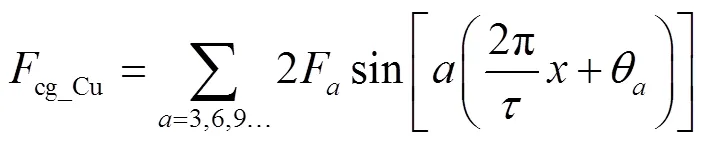
式中,cg_Au、cg_Bu、cg_Cu分别为A、B、C三相单元电机的齿槽定位力;F和θ分别为单元电机齿槽定位力的第次谐波分量的幅值及相位;是次级位置。
该电机的齿槽定位力等于各相所有单元电机的齿槽定位力之和,其表达式为
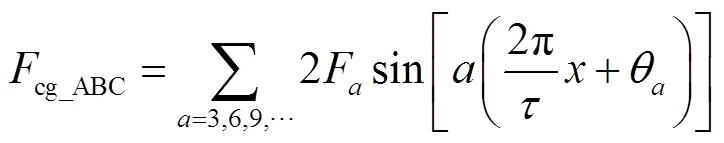
由式(4)可知,该电机的齿槽定位力谐波次数均为3的倍数。最低次的谐波分量为3次,周期为/3。
该电机端部定位力由初级两端永磁体和次级铁心单元相互作用而产生。根据文献[17],单元电机的端部定位力由左右两端的端部定位力组成,分别为u-和u+,如图4所示。若已知右手端的定位力为u+,则可通过镜像获得左手端的定位力u-。其中u+的傅里叶表达式为
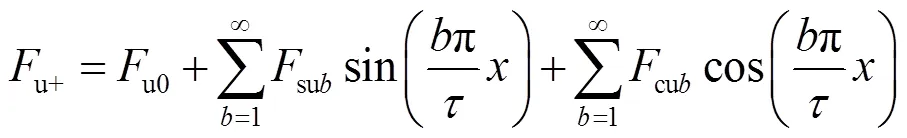
式中,和、分别为单元电机单边端部定位力的平均值和第b次谐波分量(正弦、余弦)幅值。
u-的傅里叶表达式为

因此,任意一相各单元电机的端部定位力之和为
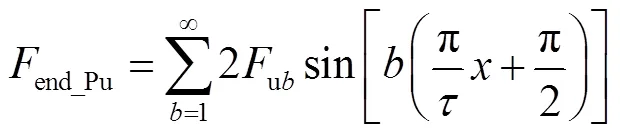
式中,ub代表任意一相的端部定位力的第次谐波分量的幅值,其值为
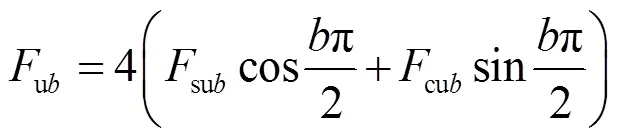
该电机的端部定位力为
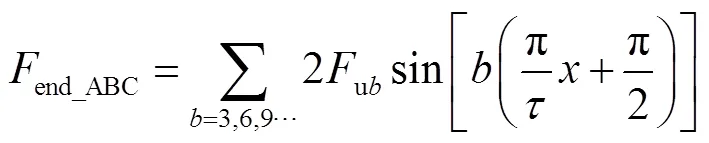
从式(9)可知,该电机的端部定位力的谐波次数均为3的倍数。最低次谐波分量为3次,周期为2/3。
图5给出该电机定位力仿真波形。如图5所示,该电机的定位力周期为/3,其峰值为7.9N,且峰值波动周期为2/3,与该电机的端部定位力的3次谐波分量周期保持一致。
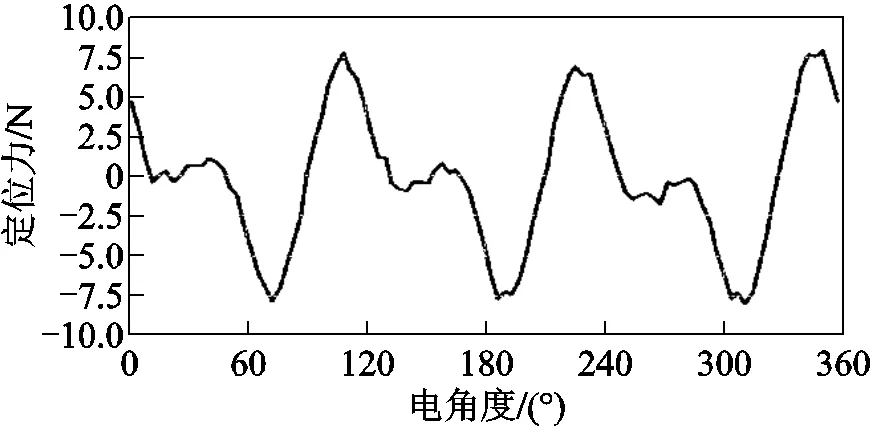
图5 定位力仿真波形
图6给出该电机定位力仿真波形谐波分析结果。如图6所示,该电机定位力主要由3次及6次谐波分量组成,分别对应端部定位力和齿槽定位力,其幅值分别为4.5N及3.74N,该结果表明端部定位力是导致该电机定位力峰值波动的原因。

图6 定位力谐波分量Fig.6 Harmonic component of the detent force
3 位置环二阶ADRC设计
3.1 TRTFLM数学模型
与传统的永磁同步直线电机相比,TRTFLM次级没有随位置变化的永磁体,但由于次级铁心的磁场调制作用,使其空载反电动势基本成正弦变化[2]。因此,基于合成磁动势不变的坐标变换及电机统一理论,该电机可依据传统永磁同步直线电机建模的思想进行建模,其在dq轴坐标系下的机械运动方程为
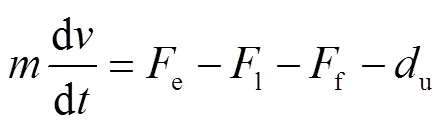
式中,为次级的质量;为次级运动速度;e为电磁推力;l为负载拉力;f为摩擦力;u为系统的未建模扰动。
采用d=0的矢量控制方式,电磁推力与交轴电流q成正比例关系,因此,机械运动方程式(10)可简化为二阶系统,即
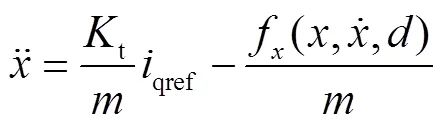

选择次级位置为状态变量1,次级运动速度为状态变量2,系统扩张的总和扰动为状态变量3,则由该电机的机械运动方程可得被控对象的状态方程为
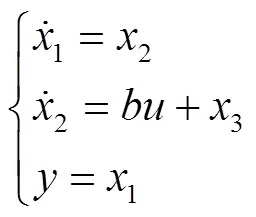
式中,为系统控制增益,其值为t/;控制量为交轴电流给定值qref。
3.2 安排过渡过程
与传统位置环、速度环及电流环三闭环级联控制相比,基于二阶ADRC的位置环控制系统采用位置与速度双闭环并联设计。因此,位置环的输出不再作为速度环的给定,而是同位置环一样,给定在次级运动之前就已被安排。图7给出了安排过渡过程基本框图。其中,为控制量可取的最大值;为采样周期;fhan是最速控制综合函数,表达式如式(13)所示,其输出值为或-,即此函数以给定的加速度值可以最快地逼近给定值。
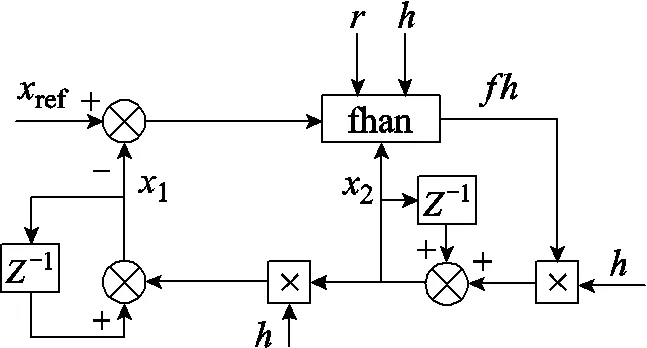
图7 安排过渡过程基本框图

式中,sign()为符号函数,>0时,sign()=1;<0时,sign()=-1;=0时,sign()=0。
3.3 三阶线性扩张状态观测器
基于线性函数的扩张状态观测器(Extended State Observer,ESO)的算法简单,可以大大减轻控制单元数据处理对硬件的压力[18]。因此,本文所提位置环二阶ADRC采用基于线性函数的ESO。
对式(12)表示的系统建立其对应的三阶线性ESO,为

式中,e为系统次级位置输出量与实际观测值之间的误差;z1、z2及z3分别为位移观测值、速度观测值及扰动观测值;1、2、3为ESO增益。
基于安排过渡过程及三阶线性ESO,本文构建了位置环二阶ADRC,其框图如图8所示。其中,安排过渡过程给出了位置与速度给定,位置环与速度环两者之间并联;基于系统控制量及实际位置值,三阶线性ESO如图8中点画线框部分所示,可以估计出该系统次级位移、速度及系统总和扰动,进而参与系统闭环控制。
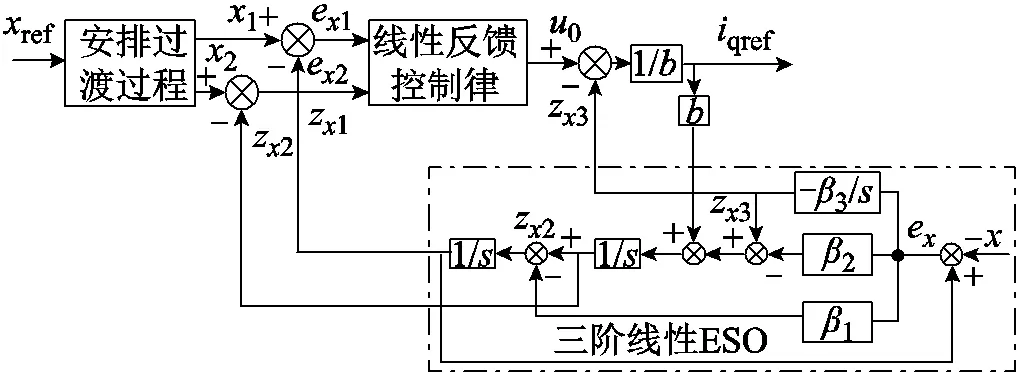
图8 位置环二阶ADRC框图
基于图8所示位置环二阶ADRC,本节进一步给出了d=0矢量控制系统,其框图如图9所示。
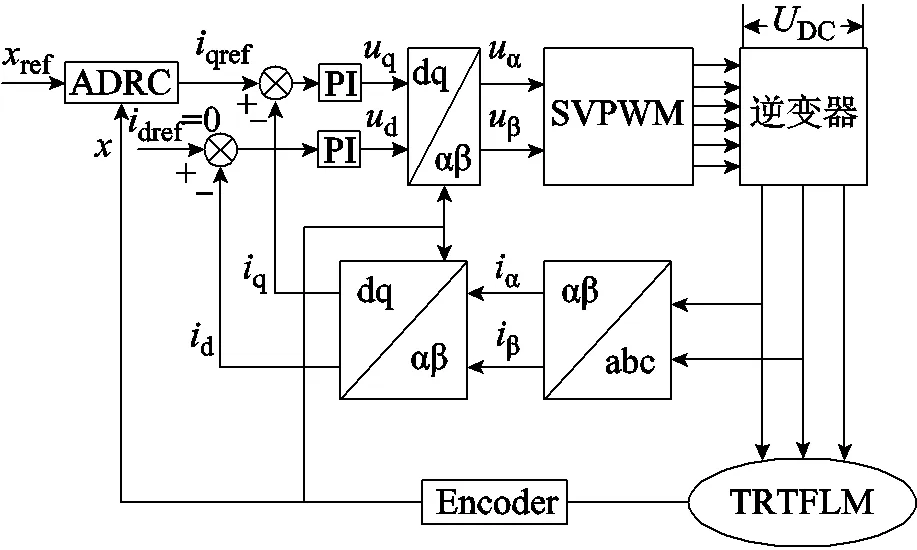
图9 基于位置环二阶ADRC的id=0矢量控制框图
4 基于定位力补偿的二阶ADRC
ESO对系统扰动估计的准确度是衡量ADRC性能的关键指标。ESO的特点是不需要依赖具体系统模型实现对扰动的估计,但当系统扰动比较复杂或幅值较大时,其观测压力将增加,系统扰动跟踪的快速性和准确性会受到影响[19]。本文考虑到该电机定位力模型已知,为减小三阶线性ESO的观测压力,进一步抑制定位力对位置环跟踪性能的影响,将定位力模型嵌入至三阶线性ESO中,设计了一种定位力补偿三阶线性ESO。并在此基础上,构建了一种定位力补偿二阶ADRC。其中,定位力补偿三阶线性ESO状态方程为
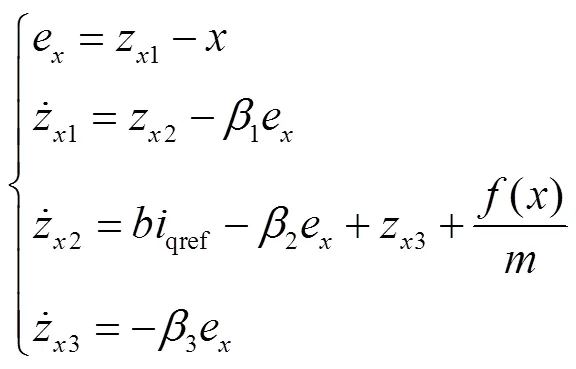
式中,()为该电机的定位力模型,根据图6的分析结果,其表达式可简化为
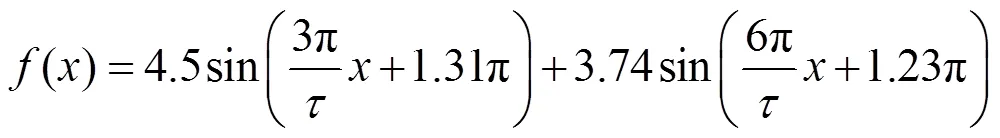
式(15)对应的控制框图如图10所示。
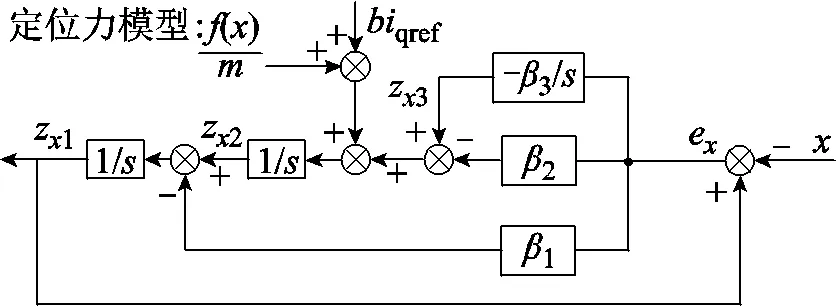
图10 定位力补偿ESO控制框图
由图8及图10可以推出该电机位置环定位力补偿二阶ADRC框图,如图11所示。其中,点画线框内为定位力补偿三阶线性ESO。
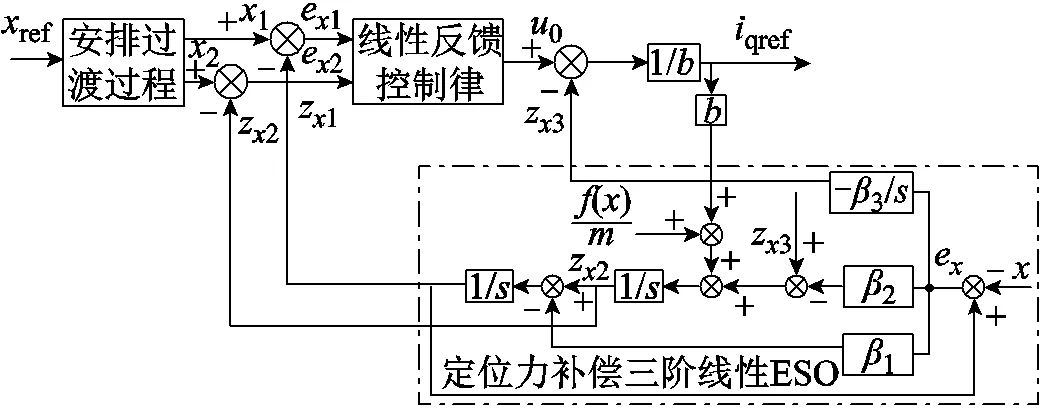
图11 位置环定位力补偿二阶ADRC框图
5 实验验证
为验证控制方案在该电机上应用的可行性,本文基于TI公司TMS320F28335浮点处理器为控制核心,搭建控制系统的硬件平台及软件平台。图12给出该电机控制算法验证用实验平台。实验平台主要由直流电源、控制板、功率板、初级、次级、光栅尺及示波器等部件组成。实验主要参数如下:次级运动速度给定取0.1m/s,次级质量为20kg,电机负载17N。

图12 控制算法验证用实验平台
5.1 位置环抗扰性能
图13给出了突加17N负载情况下的位置动态响应实验波形。如图13a所示,当系统采用PI控制器时,系统恢复时间为0.74s,位置偏差峰值为0.98mm;如图13b所示,当系统采用二阶ADRC时,系统恢复时间为0.36s,位置偏差峰值为0.065mm。
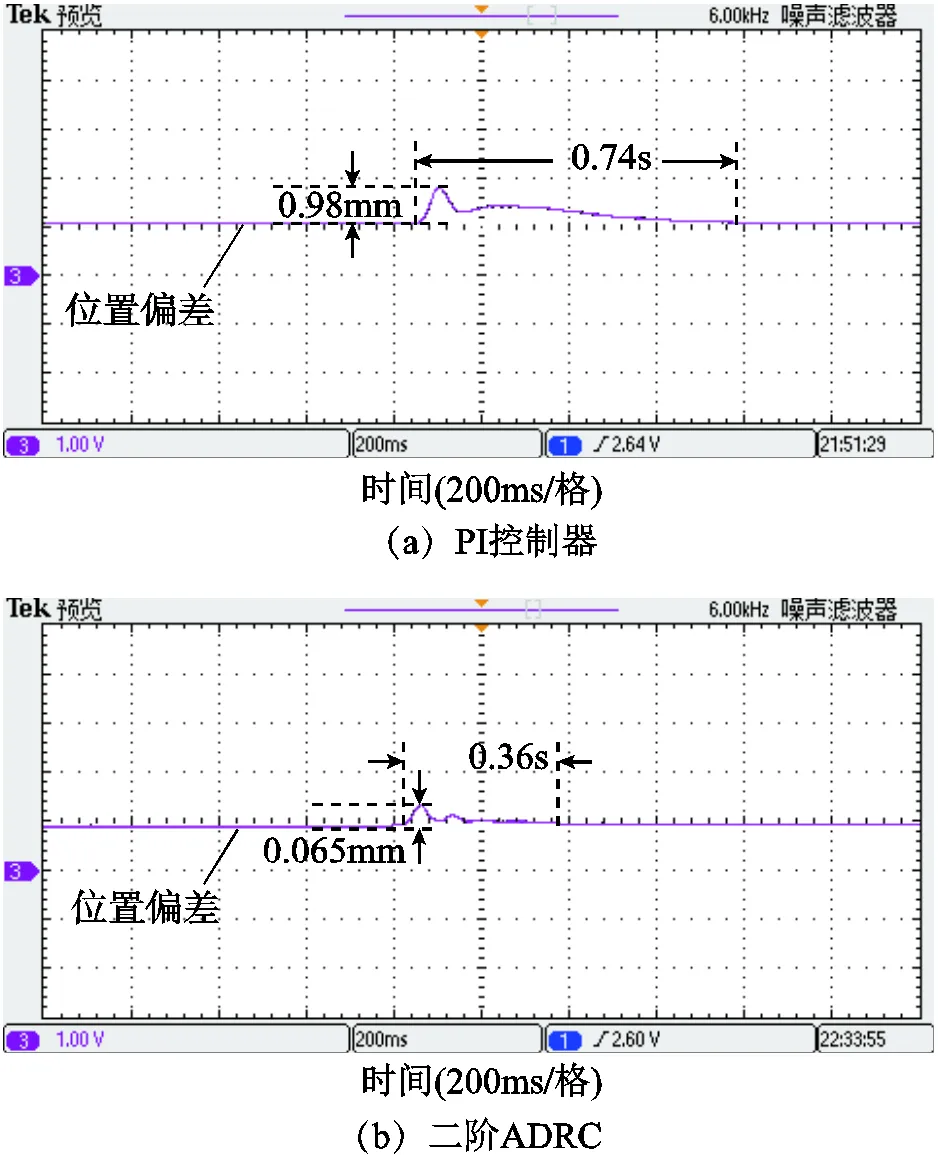
图13 突加负载的动态响应实验波形
图14给出了突卸17N负载情况下的位置动态响应实验波形。如图14a所示,当系统采用PI控制器时,系统恢复时间为0.6s,位置偏差峰值为1.25mm;如图14b所示,当系统采用二阶ADRC时,系统恢复时间为0.32s,位置偏差峰值为0.087mm。
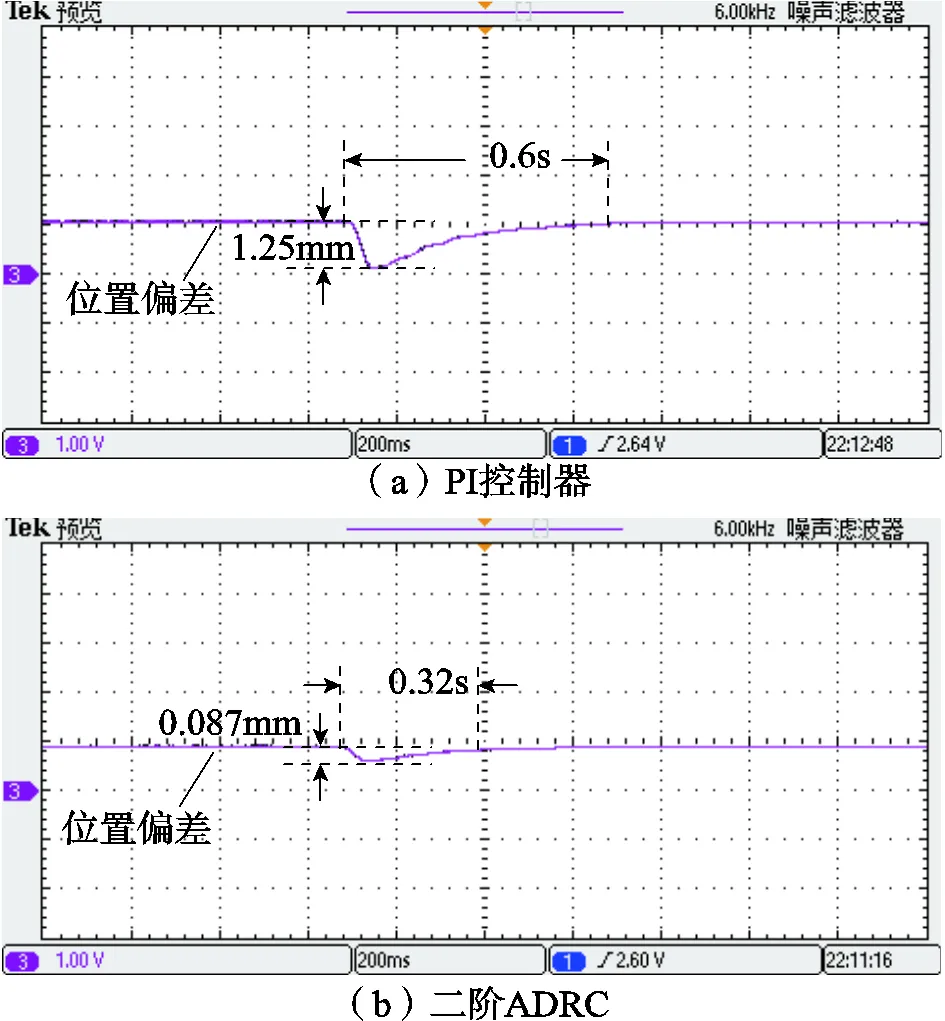
图14 突卸负载的动态响应实验波形
综上所述,与PI控制器相比,基于二阶ADRC的位置环控制具有更好的抗扰性能。
5.2 位置环跟踪性能
阶跃位置给定为20cm,电流环均采用PI控制器。在空载条件下起动电机,同时,保持系统不出现超调。图15给出了空载情况下阶跃位置给定动态响应实验波形。如图15a所示,当系统采用PI控制器时,系统调节时间为0.74s;如图15b所示,当系统采用二阶ADRC时,系统调节时间为0.56s。
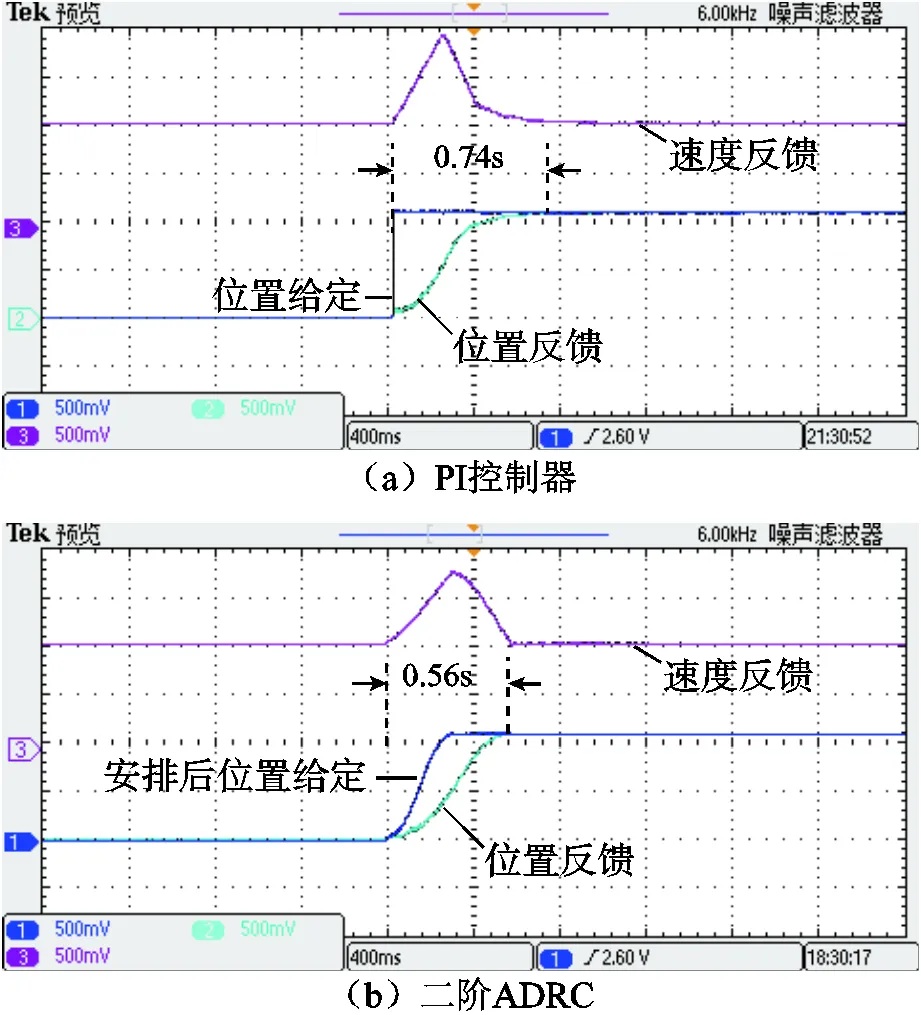
图15 阶跃位置给定动态响应实验波形
为考察系统对连续变化的输入信号的跟踪能力,图16给出了空载情况下正弦输入信号的动态响应仿真波形,其中,给定频率为0.5Hz,位置幅值取0.05m。如图16a所示,当系统采用PI控制器时,位置反馈与位置给定之间的位置偏差峰峰值为0.29mm;如图16b所示,当系统采用二阶ADRC时,位置反馈与位置给定之间的位置偏差峰峰值为0.064mm;如图16c所示,给出了定位力补偿二阶ADRC的正弦位置给定动态响应实验波形,位置反馈与位置给定之间的位置偏差峰峰值为0.048mm。
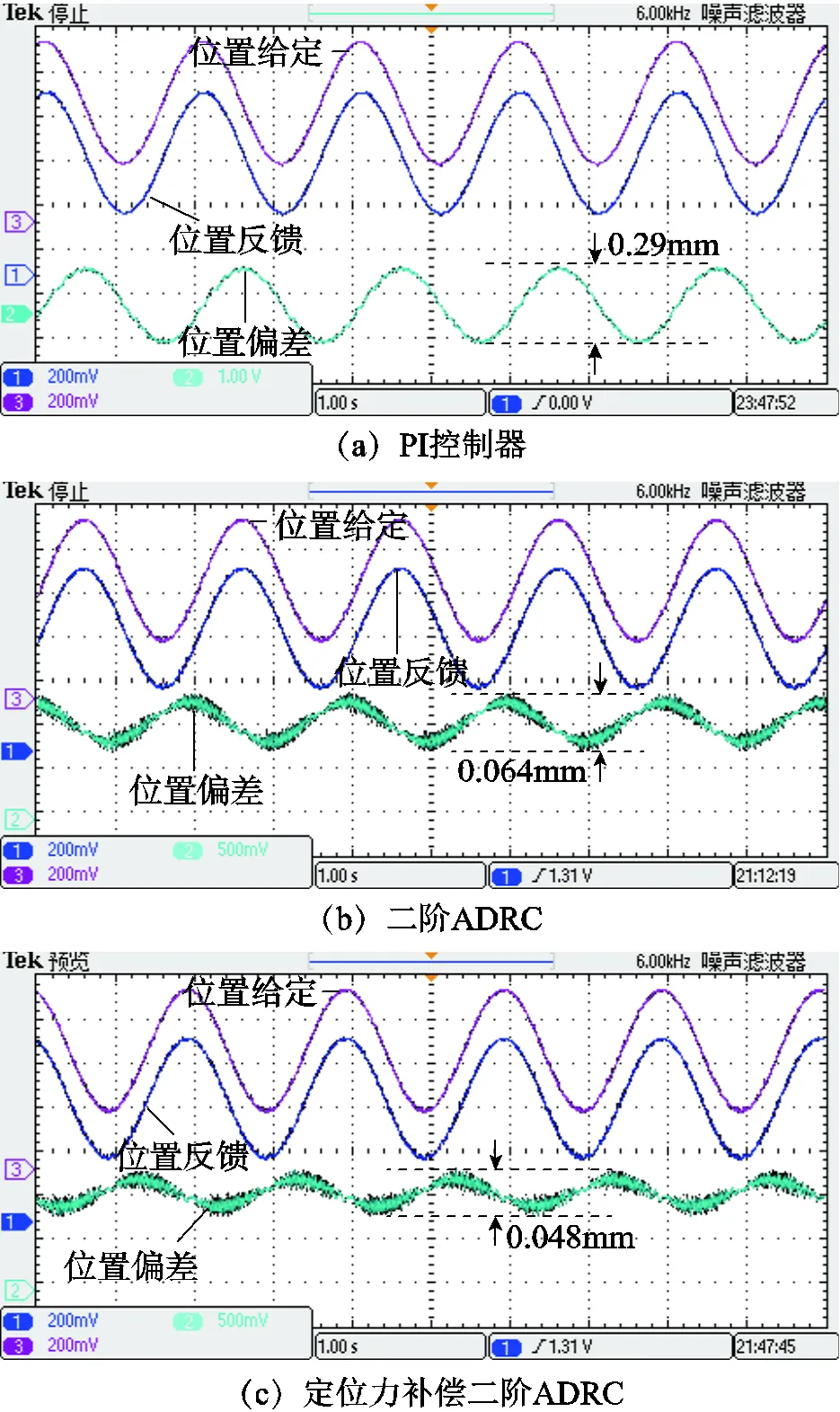
图16 正弦位置给定动态响应实验波形
综上所述,与PI控制器及二阶ADRC相比,定位力补偿二阶ADRC位置控制具有更好的跟踪性能。
6 结论
本文从TRTFLM位置控制的抗扰性能及跟踪性能的角度出发,对位置环与速度环进行并联设计,构建了位置环二阶ADRC。考虑定位力对该电机的影响,进一步提出了一种定位力补偿二阶ADRC。实验结果表明本文研究的位置环二阶ADRC控制策略在该新型拓扑结构电机位置控制上相比PI控制器具有较好的抗扰性能及跟踪性能。同时,本文所提出的定位力补偿二阶ADRC有利于位置跟踪性能的进一步改善,说明该方法具有一定的工程应用价值,可为该新型磁通反向式横向磁通永磁直线电机的位置控制提供一定的参考。
[1]董顶峰, 黄文新, 卜飞飞, 等. 绕组周向分布圆筒型初级永磁直线电机结构及静态特性分析[J]. 中国电机工程学报, 2017, 37(21): 6181-6189. Dong Dingfeng, Huang Wenxin, Bu Feifei, et al. Structure and static characteristic analysis of tubular primary permanent magnet linear machine with circumferential distribution of winding[J]. Proceedings of the CSEE, 2017, 37(21): 6181-6189.
[2]罗俊, 寇宝泉, 杨小宝. 双交替极横向磁通直线电机的优化与设计[J]. 电工技术学报, 2020, 35(5): 991-1000. Luo Jun, Kou Baoquan, Yang Xiaobao. Optimization and design of dual-consequent-pole transverse flux linear machine[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 991-1000.
[3]曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020, 35(5): 1001-1012. Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001-1012.
[4]姬相超, 赵希梅. 永磁直线同步电动机的自适应时滞控制[J]. 电工技术学报, 2020, 35(6): 1231-1238. Ji Xiangchao, Zhao Ximei. Adaptive time delay control of permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1231-1238.
[5]黄庆, 黄守道, 伍倩倩, 等. 基于模糊自抗扰控制器的永磁同步电动机伺服系统[J]. 电工技术学报, 2013, 28(9): 294-301. Huang Qing, Huang Shoudao, Wu Qianqian, et al. PMSM servo system based on fuzzy active-disturbance rejection controller[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 294-301.
[6]左月飞, 张捷, 刘闯, 等. 基于自抗扰控制的永磁同步电机位置伺服系统一体化设计[J]. 电工技术学报, 2016, 31(11): 51-58. Zuo Yuefei, Zhang Jie, Liu Chuang, et al. Integrated design for permanent magnet synchronous motor servo system based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 51-58.
[7]韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23. Han Jingqing. Auto-disturbances-rejection controller andits applications[J]. Control and Decision, 1998, 13(1): 19-23.
[8]韩京清. 自抗扰控制技术—估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
[9]朱进权, 葛琼璇, 孙鹏琨, 等. 基于自抗扰的高速磁浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(5): 1065-1074. Zhu Jinquan, Ge Qiongxuan, Sun Pengkun, et al. Traction-system research of high-speed maglev based on active disturbance rejection control[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1065-1074.
[10]Li Longfei, Xiao Jie, Zhao Yun, et al. Robust position anti-interference control for PMSM servo system with uncertain disturbance[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 151-160.
[11]Su Y X, Zheng C H, Duan B Y. Automatic disturbances rejection controller for precise motion control of permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2005, 52(3): 814-823.
[12]孙凯, 许镇琳, 盖廓, 等. 基于自抗扰控制器的永磁同步电机位置伺服系统[J]. 中国电机工程学报, 2007, 27(15): 43-46. Sun Kai, Xu Zhenlin, Gai Kuo, et al. A novel position controller of PMSM servo system based on active-disturbance rejection controller[J]. Proceedings of the CSEE, 2007, 27(15): 43-46.
[13]刘春强, 骆光照, 涂文聪, 等. 基于自抗扰控制的双环伺服系统[J]. 中国电机工程学报, 2017, 37(23): 7032-7039. Liu Chunqiang, Luo Guangzhao, Tu Wencong, et al. Servo systems with double closed-loops based on active disturbance rejection controllers[J]. Proceedings of the CSEE, 2017, 37(23): 7032-7039.
[14]左月飞, 张捷, 刘闯, 等. 针对时变输入的永磁同步电机改进型自抗扰控制器[J]. 电工技术学报, 2017, 32(2): 161-170. Zuo Yuefei, Zhang Jie, Liu Chuang, et al. A modified adaptive disturbance rejection controller for permanent magnetic synchronous motor speed-regulation system with time-varying input[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 161-170.
[15]郭凯凯, 郭有光. 磁通反向直线旋转永磁电机三维非线性等效磁路模型分析[J]. 电工技术学报, 2020, 35(20): 4278-4286. Guo Kaikai, Guo Youguang. 3D nonlinear equivalent magnetic circuit model analysis of a flux reversal linear rotary permanent magnet machine[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4278-4286.
[16]Zou Jibin, Zhaomei, Wang Qian, et al. Development and analysis of tubular transverse flux machine with permanent magnet excitation[J]. IEEE Transactions on Industrial Electronics, 2012, 59(5): 2198-2207.
[17]Kou Baoquan, Luojun, Yang Xiaobao, et al. Modeling and analysis of a novel transverse-flux flux-reversal linear motor for long-stroke application[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6238-6248.
[18]刘志刚, 李世华. 基于永磁同步电机模型辨识与补偿的自抗扰控制器[J]. 中国电机工程学报, 2008, 28(24): 118-123. Liu Zhigang, Li Shihua. Active disturbance rejection controller based on permanent magnetic synchronous motor model identification and compensation[J]. Proceedings of the CSEE, 2008, 28(24): 118-123.
[19]刘星桥, 胡建群, 周丽. 自抗扰控制器在三电机同步系统中的应用[J]. 中国电机工程学报, 2010, 30(12): 80-85. Liu Xingqiao, Hu Jianqun, Zhou Li. Active disturbance rejection control of three-motor synchronous control system[J]. Proceedings of the CSEE, 2010, 30(12): 80-85.
Second-Order ADRC Position Control with Detent Force Compensation for Tubular Reversal Transverse Flux Linear Machine
Dong Dingfeng1,2Huang Wenxin2Bu Feifei2Huang Weikang2Jiang Wen2
(1. Nanjing ESTUN Automation Co. Ltd Nanjing 211106 China 2. College of Automation Engineering Nanjing University of Aeronautics and Astronautics Nanjing 211106 China)
In order to reduce the influence of detent force, friction force and load disturbance on the position control performance for tubular reversal transverse flux linear machine (TRTFLM), a second-order active disturbance rejection control (ADRC) with detent force compensation is proposed. First, the basic structure and working principle of the machine are given, and the generating mechanism, mathematical model and harmonic component of the detent force are analyzed. Then, based on the mathematical model of the machine, the position loop and speed loop are designed in parallel, and the second-order ADRC of the position loop is constructed, which improves the disturbance rejection and tracking performance of the position control of the TRTFLM. On this basis, the detent force model is embedded into the extended state observer (ESO) to optimize the second-order ADRC, which further improves the tracking performance of the position control. Finally, the experimental results show that the control scheme is feasible and effective.
Tubular reversal transverse flux linear machine, detent force, active disturbance rejection control, position control
TM351
10.19595/j.cnki.1000-6753.tces. 201066
2020-08-30
2020-11-19
董顶峰 男,1982年生,博士,研究方向为新型永磁同步直线电机设计及其控制。E-mail:dong_dingfeng@126.com(通信作者)
黄文新 男,1966年生,博士,教授,博士生导师,研究方向为电机及其控制、新型风力发电技术、电能变换、航空电源等。E-mail:huangwx@nuaa.edu.cn
(编辑 郭丽军)
