分段长初级双边直线感应电动机建模分析

张明远 史黎明 郭科宇 杨泽宇 徐 飞

分段长初级双边直线感应电动机建模分析

张明远1,2史黎明1郭科宇1,2杨泽宇1徐 飞1

（1. 中国科学院电力电子与电力驱动重点实验室（中国科学院电工研究所） 北京 100190 2. 中国科学院大学 北京 100049）

分段长初级双边直线感应电动机（LP-DSLIM）系统由若干段单元电机串联或并联组成，为准确描述次级运动过程中单元电机的推力等状态变化和过分段时的暂态过程，该文提出了一种新型单元电机数学模型及分段LP-DSLIM系统模型。首先，对分段LP-DSLIM系统的特点进行分析，通过引入虚拟次级板将每段单元电机耦合的次级延长至与初级等长，以使单元电机初级、次级之间始终保持全耦合；然后，结合耦合因数得到实际次级磁链和初级磁链，以此推导得到新型单元电机数学模型，并基于此建立串联供电和并联供电的分段LP-DSLIM系统模型；最后，有限元计算和实验结果验证了提出的新型单元电机数学模型和分段LP-DSLIM系统模型的正确性。

长初级双边直线感应电动机 单元电机 数学模型 虚拟次级 耦合因数

0 引言

长初级双边直线感应电动机（Long Primary Double-Sided Linear Induction Motor, LP-DSLIM）的次级一般为铝板，质量较轻，且装置的体积较小，结构简单，可靠性高，在高速时边端效应小，推力密度大，被广泛应用在汽车碰撞、轨道交通和电磁加速领域[1-3]。已有文献分别从电机特性[4]、边端效应[5-8]、控制方法[9-12]及解析计算[13-16]等多个角度对LP-DSLIM进行了研究。

LP-DSLIM次级长度比初级长度短，电机漏感很大，电压利用率低，在运行过程中会产生大量的无功功率。为提高电压利用率和效率、节约电能并减小对电源容量的要求，在实际应用中常将初级分段，如图1所示，并采用分段供电的驱动方式[17-18]。

图1 分段LP-DSLIM系统示意图

分段LP-DSLIM中每个分段都可以看作一段单元电机。随着次级的直线运动，初级、次级之间的耦合状况发生变化，由此导致各段单元电机参数变化。每段单元电机都会经历次级进入—全耦合—离开的过程[19]，如图2所示。每段电机的参数和状态不仅随次级位置时刻变化，还与上一段初级的状态有关，其数学模型的建立非常困难。

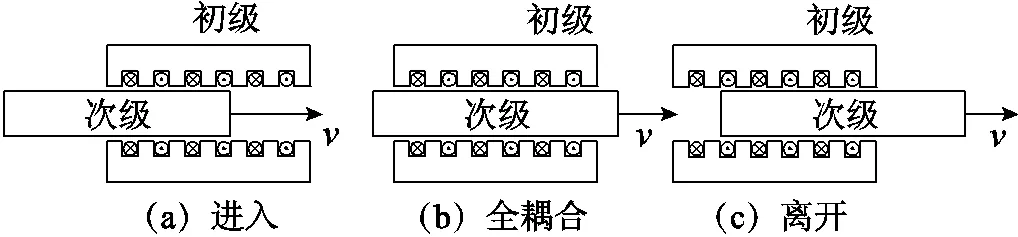
图2 分段LP-DSLIM系统次级与初级的三种耦合情况

分段LP-DSLIM系统是由若干段单元电机串联或并联组成，供电方式比较灵活，不同的供电方式系统模型有差别。为建立分段LP-DSLIM系统模型，并研究相应的控制策略，需要建立单元电机的数学模型。尤其是在分段并联的LP-DSLIM系统中，每一段电机都相对独立，无法像串联供电情况下建立通电段整体的数学模型，因此建立单元电机的数学模型具有重要意义。

目前，国内外关于分段LP-DSLIM系统的建模文献较少。文献[20]对不分段的LP-DSLIM进行建模，将LP-DSLIM分为耦合次级的有效部分和不耦合次级的无效部分，并建立了等效电路。文献[21]将覆盖次级的初级段串联供电，在次级运动过程中，次级覆盖串联通电定子段的长度始终不变，电机的参数和模型是固定不变的，由此建立了串联通电段整体的数学模型，但未对单元电机建模。文献[22]为了研究串联供电时切换策略，分别建立了串联供电段整体在切换过程中的正常模态、错位模态和并联模态的电机参数矩阵，也未对单元电机建模。文献[23-24]研究了多段初级永磁直线同步电动机驱动系统整体建模并进行仿真。

文献[25-26]借鉴文献[20]的思想，将分段LP-DSLIM中每段单元电机分为耦合次级的有效部分和不耦合次级的无效部分，用耦合因数对等效参数修正分别建立了无效部分和有效部分的数学模型以描述次级运动对单元电机的影响。但文献[20]中的耦合因数是恒定不变的，若直接将其应用在耦合因数变化的单元电机中，在次级高速运动时，单元电机的次级磁链和电磁推力的滞后现象较为明显，与实际情况相差较大。

本文推导得到了分段LP-DSLIM单元电机新型数学模型，基于新型单元电机模型分别建立了串联供电和并联供电的分段LP-DSLIM系统模型；在Simulink中对新型单元电机模型和现有文献中的单元电机模型的仿真结果进行对比分析；最后对提出的新型单元电机模型进行有限元分析和实验验证。

1 单元电机模型

将单元电机分为两部分：与次级耦合的有效部分和不与次级耦合的无效部分。设每段初级长度为1，次级与第段单元电机初级耦合的长度为D，如图3所示。

图3 单元电机示意图

定义第段单元电机的耦合因数α=D/1。当D=1时，α=1，单元电机为全耦合。对于一台全耦合的单元电机，其等效参数分别为：初级电阻s，初级漏感ls，次级电阻r，次级漏感lr，励磁电感m，极距为。初级自感s=m+ls，次级自感r=m+lr。

1.1 既有单元电机模型分析

既有单元电机模型[25-26]借鉴文献[20]中不分段LP-DSLIM的思想，将分段LP-DSLIM中每段单元电机分为耦合次级的有效部分和不耦合次级的无效部分，用耦合因数对单元电机全耦合时的参数进行修正，分别建立了无效部分和有效部分的数学模型，以描述次级运动对单元电机的影响，并将两部分相加得到单元电机模型，等效电路如图4所示。

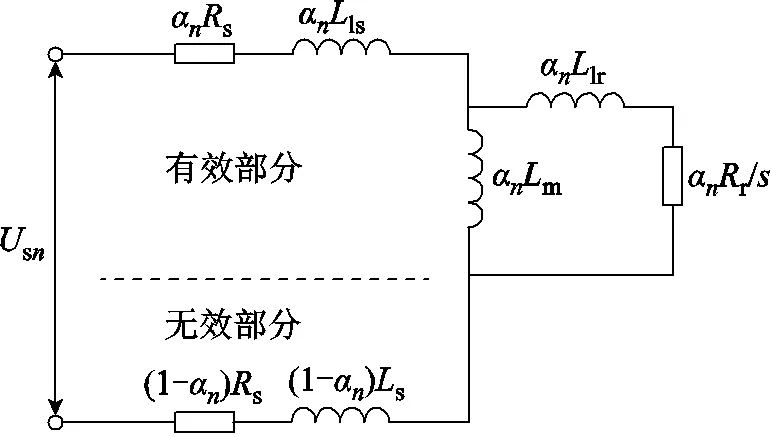
图4 既有单元电机模型等效电路

在静止两相αβ坐标系中，既有单元电机的数学模型为

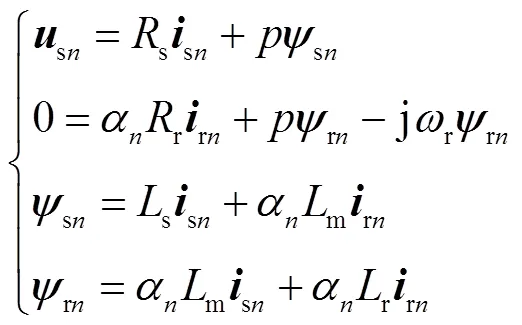
式中，sn、sn和sn分别为第段单元电机初级电压矢量、电流矢量和磁链矢量；rn和rn分别为第段单元电机次级电流矢量和磁链矢量；r=π/，为次级速度，为微分算子。

第段单元电机产生的电磁推力为

式中，×表示向量积。

式（1）和式（2）共同构成了既有单元电机数学模型。

由式（1）可推导得到次级磁链和次级电流与初级电流的关系

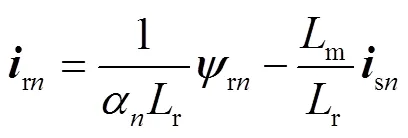
式中，r=r/r。

由式（3）可知，次级磁链与αisn为一阶惯性环节，因此在次级进入并离开一段初级的整个过程中次级磁链都滞后于耦合因数的变化。根据式（2），次级磁链的滞后会导致电磁推力的滞后。在次级完全离开这段初级后，次级磁链和电磁推力仍然会存在3r的时间才能衰减至完全离开时刻值的5%以下。而由式（4）可知，次级完全离开后，次级磁链不为0而α=0，次级电流为无穷大。根据以上分析结果可知，既有单元电机数学模型在动态情况下与实际情况相差较大。

1.2 新型单元电机模型理论推导

分析可知，LP-DSLIM次级感应板始终位于初级的励磁磁场中，气隙磁场以转差频率切割次级。在运动过程中，次级的进入端的表面磁场由空载气隙值减小到合成气隙值，次级滑出端是从气隙合成值增大到空载气隙值，LP-DSLIM边端效应比较小[5]，本文暂不考虑。

分段LP-DSLIM系统中各单元电机共用一块次级板，因此各单元电机的次级速度和次级时间常数均相同，各段初级的设计参数也保持一致。在现有分段长初级直线感应电机的文献中[17-18]，大多通过晶闸管换步控制实现覆盖次级的各初级串联供电，各段初级电流可视为完全相等。

为建立分段LP-DSLIM系统单元电机数学模型，做出如下假设：①不计磁路饱和；②铝的磁导率与空气相同；③不计长初级直线感应电机边端效应；④各段初级电流相等；⑤单元电机次级参数与初级耦合次级的长度成正比。

引入一段等高等宽的虚拟次级板，将每段单元电机耦合的次级延长至与初级等长，如图5所示。

图5 虚拟次级示意图

直线感应电动机次级为铝板，铝的磁导率与空气基本相同，因此虚拟次级板的引入不会改变单元电机内无效部分磁路的磁导率，也不会改变单元电机的初级参数。

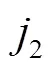
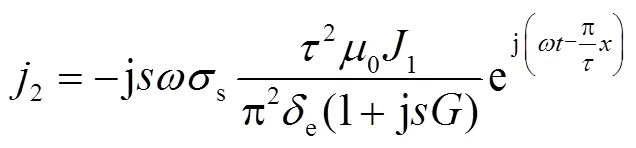
式中，j为虚数单位；1为初级电流密度幅值；为初级电流角速度；为转差率；为坐标轴；s为次级表面电导率；0为真空磁导率；e为气隙宽度；为品质因数。

由式（5）可知，次级板上的电流密度分布与次级长度无关，而电流矢量与电流密度相对应，因此得到如下结论：次级电流矢量仅与初级电流激励有关，与耦合的次级长度无关。为证明上述理论的正确性，分别将次级置于一段初级的不同位置，如图6所示，并施加相同的初级电流激励进行时谐涡流场分析。以初级为参考坐标系，在时谐涡流场分析结果中，次级电流密度沿轴上的基波分量如图7所示。

图6 次级位置示意图

图7 次级电流密度分布

不同长度次级上的次级电流密度2n沿轴分布的表达式均为

式中，2n为次级电流密度的幅值；与电机参数和转差率有关；0为某一时刻。

电流矢量与电流密度分布对应，由式（6）可得，不同长度次级的次级电流矢量表达式均为

式中，rn为次级电流矢量的幅值。

由此证明，次级电流矢量仅与初级电流激励有关，与耦合的次级长度无关。因此在相同的初级电流激励下，实际的次级电流矢量与虚拟延长次级至初级等长后的次级电流矢量相等。

在既有单元电机模型中，直接采用耦合因数对全耦合时的电机参数进行修正得到有效部分和无效部分来描述次级的运动，导致次级电流出现无穷大，电机模型明显失准。因此为了得到准确的次级电流，通过虚拟延长次级板至与单元电机初级等长，使得单元电机始终处于全耦合状态，单元电机的参数不再随次级位置变化而变化，在这种情况下得到的次级电流矢量与实际次级电流矢量相等。在静止两相αβ坐标系中，可得到次级电流、次级磁链与初级电流的关系为

式（8）包含了分段LP-DSLIM系统中次级由第段单元电机进入第+1段单元电机过程中携带了由段单元电机激励的次级涡流的特性。

式（8）中的次级电流矢量即为实际次级电流矢量。但需要注意的是，这里的r是第段单元电机计及实际次级和虚拟次级的总次级磁链。单元电机次级参数与初级耦合次级的长度成正比，因此将次级自感修正为αLr，将次级与初级线圈的互感修正为αLm，那么第段单元电机的实际次级磁链ro即为

实际次级产生的磁通才会交链到初级线圈，虚拟次级产生的磁通不会作用到初级。次级电流矢量通过修正后的互感αLm作用到初级线圈，因此第段单元电机初级磁链方程即为

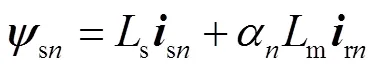
第段单元电机初级电压方程为

式（8）～式（11）共同构成了第段单元电机的电压方程和磁链方程，即

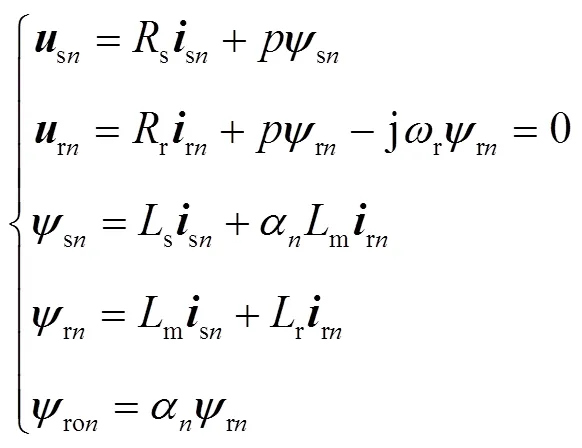
第段单元电机产生的电磁推力为

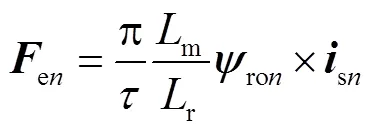
式（12）和式（13）共同构成了新型单元电机数学模型。

选取初级电流sn和次级磁链rn为状态变量，sn为输入变量，第段单元电机的状态方程为

其中

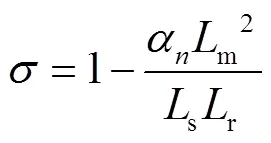
推力作为输出量，第段单元电机的输出方程为

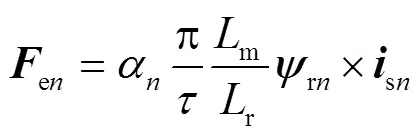
2 基于新型单元电机模型的分段LP-DSLIM系统模型

分段LP-DSLIM系统通常有两种供电方式：串联供电和并联供电。不同供电方式下，基于单元电机模型建立的分段LP-DSLIM系统模型也不同。

2.1 串联供电系统模型

假设次级最多耦合段初级，当采用串联供电方式时，通过晶闸管换步将耦合以及即将耦合次级的段单元电机串联通电，此时段单元电机看成一台电机，其等效参数为单元电机等效参数的倍。次级长度为2，则耦合因数始终为2/(1)。据此对式（12）和式（13）的参数进行修正即可得到串联通电段整体的数学模型，即为

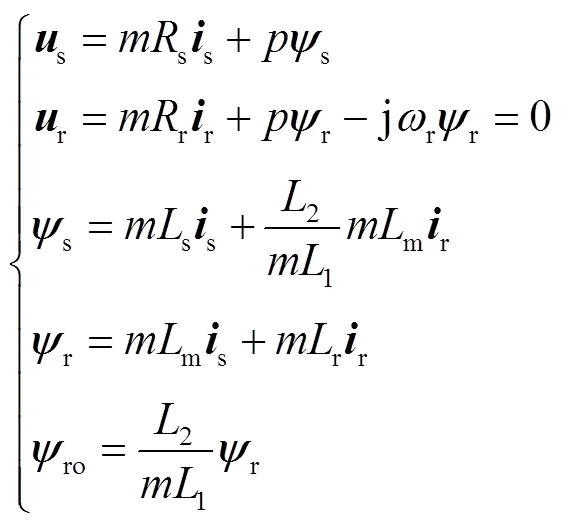
式中，s、s和s分别为串联通电段整体初级的电压、电流和磁链矢量；r和r分别为次级与串联通电的初级等长时的次级电压和次级磁链矢量；ro和r分别为实际次级的次级磁链和次级电流矢量。

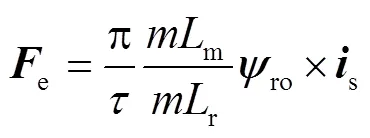
为物理概念清晰，保留公式中分子分母上可以约分的。注意到串联通电段整体的电压和磁链方程的参数是固定不变的，此时等效为真正的LP-DSLIM，与文献[20-21]中LP-DSLIM模型等效。

2.2 并联供电系统模型

当采用并联供电方式时，基于新型单元电机模型建立的分段并联LP-DSLIM系统如图8所示。图中所有单元电机模型都基于式（14）～式（16）。

图8 由新型单元电机模型建立的分段并联 LP-DSLIM系统

所有单元电机的电磁推力共同作用到次级，次级运动模块的方程为

式中，、和d分别为次级的加速度、速度和位移；为计及风阻、摩擦力等的总阻力。

各段单元电机的耦合因数根据次级位置计算得到。

串联供电系统模型只能研究串联通电段整体的电磁推力和次级磁链特性，无法研究各单元电机的特性，因此本文的仿真和验证都是基于较为复杂的并联供电系统模型。

3 仿真结果分析

表1 单元电机参数

Tab.1 The parameters of unit motor model

控制两个系统中各段初级电流相等，采用恒电流转差频率控制，初级电流的有效值为3kA，转差频率取电机推力特性稳定区域的中间为slip=0.4Hz，次级速度从0开始加速，基于新型单元电机模型和既有单元电机模型的分段并联LP-DSLIM系统的耦合因数、次级总推力及各单元电机推力、次级磁链、速度、电流和电压波形分别如图9和图10所示。

在图9中，随次级的运动，新型单元电机模型次级磁链和电磁推力与其耦合因数成正比。只有与次级耦合的单元电机才会产生推力，总推力为所有与次级发生耦合的单元电机推力之和。

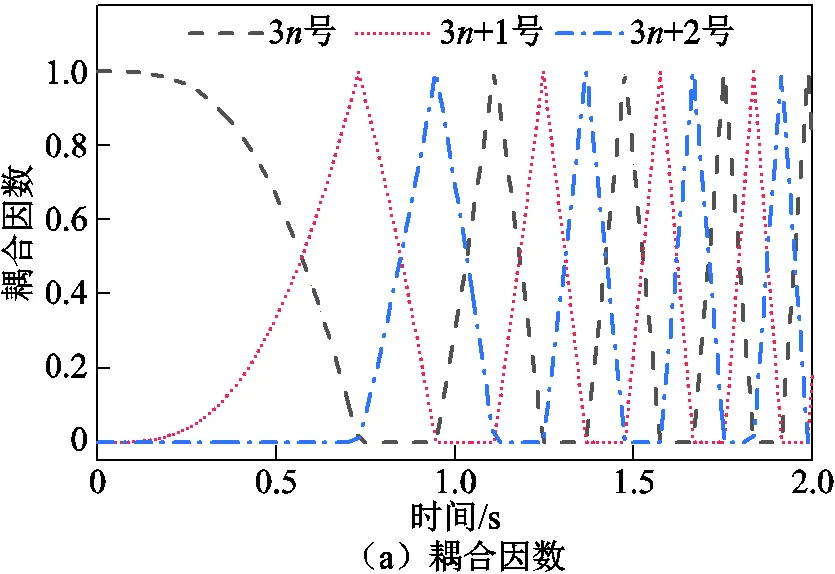
在图10中，既有单元电机模型次级磁链和电磁推力均滞后于耦合因子，在次级离开后还能保持较长时间，此结果与1.1节中理论分析一致。单元电机产生的最大推力和次级磁链的最大值随速度的增大而减小，如图10b和图10c所示。这是因为随着次级速度增大，每段电机的定子电流αisn作用的时间减少，由式（3）中一阶惯性环节可得此特性。次级离开一段初级后，次级磁链和电磁推力衰减的时间是一定的，为3r，因此同时产生电磁推力的单元电机数量随速度的增大而增加。

当各段单元电机初级电流相等时，次级板表面磁场平均分布，各段单元电机的次级磁链与其耦合次级的长度成正比，即与耦合因数成正比，因此电磁推力与耦合因数成正比。文献[17]对现有分段供电进行了综述，均是将只与次级耦合的初级通电，其他初级不通电；在文献[18, 22]中对分段LP-DSLIM串联供电，研究了切换的过程并进行了实验，没有因为只给与次级耦合的初级通电导致推力损失和波动。按照既有单元电机模型分析，需要对同时产生推力的多段不耦合次级的初级也通电，若只对与初级耦合的单元电机通电，则必会导致推力的波动和损失，与现有研究结果差异较大。因此新型单元电机模型可以更准确地描述单元电机及分段LP-DSLIM系统。

4 有限元分析

为了进一步验证新型单元电机模型及分段LP-DSLIM系统的正确性，本文利用Ansys公司的Maxwell仿真环境进行有限元分析。

在恒定初级电流有效值3kA条件下，单元电机全耦合时堵转推力特性曲线如图11所示。基于新型单元电机数学模型的Simulink仿真结果与有限元计算结果之间误差较小。

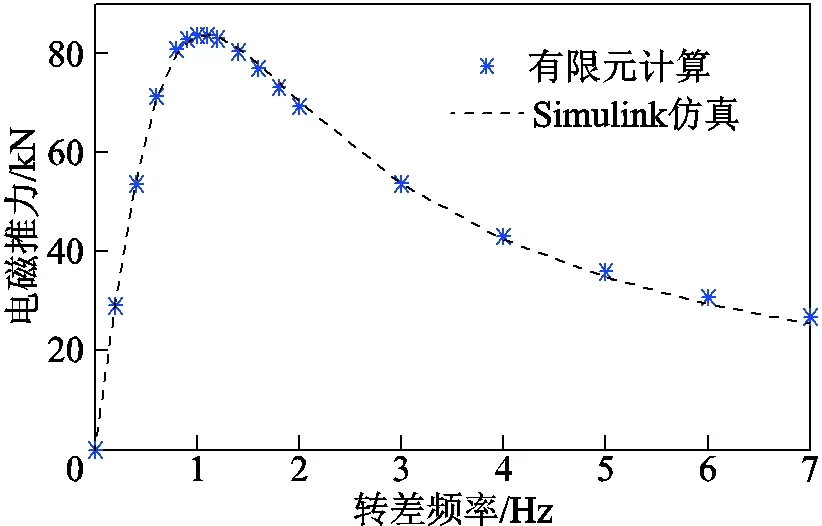
图11 单元电机推力特性曲线

图12为在恒初级电流有效值3kA下单元电机堵转电磁推力随耦合因数的变化曲线。基于新型单元电机模型的Simulink仿真结果与有限元计算结果一致，不同转差频率下电磁推力均与耦合因数成正比。由电磁推力的生成机理分析可知，次级磁链也与耦合因数成正比。这个结果表明新型单元电机模型中引入虚拟次级和耦合因数的理论是正确的。

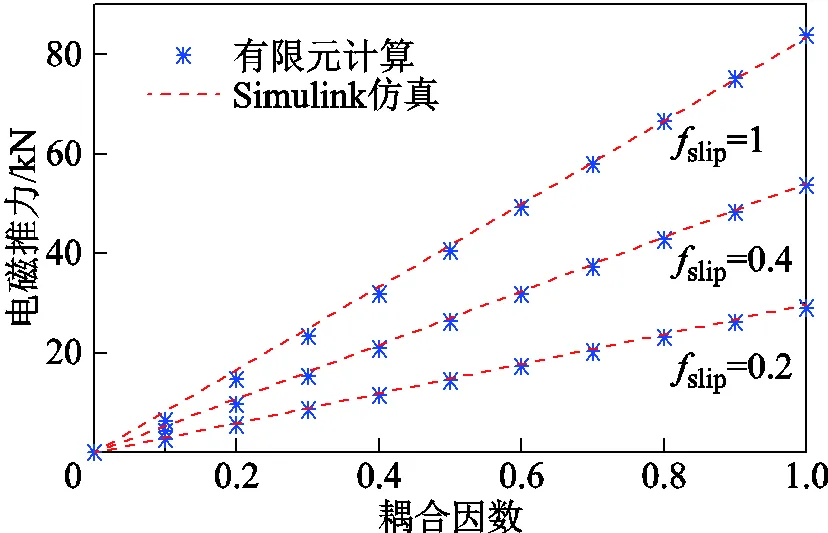
图12 电磁推力随耦合因数变化曲线

控制次级速度始终为20m/s，采用恒电流转差频率控制，电流的有效值为3kA，转差频率为slip=0.4Hz，次级运动过程总电磁推力曲线如图13a所示。基于新型单元电机模型的分段并联LP-DSLIM系统稳态推力基本等于有限元计算的推力中值。在有限元计算结果中推力波动是由于动态边端效应引起的，频率为0.8Hz，为转差频率0.4Hz的两倍。为观察各单元电机电磁推力变化，提取3～4s内次级耦合的各单元电机电磁推力曲线如图13b所示，两种结果的各单元电机电磁推力非常接近，均与耦合因数成正比。分段LP-DSLIM系统Simulink仿真结果与有限元结果吻合良好，证明了新型单元电机模型及基于其建立的分段LP-DSLIM系统的准确性。

5 实验验证

基于分段长初级直线感应电机样机对新型单元电机模型理论进行验证，实验平台如图14所示。

图14 分段LP-DSLIM实验平台

给一段初级通电，使次级与通电初级耦合不同的长度。在初级电流有效值10A、转差频率为5Hz下，单元电机堵转电磁推力在不同耦合因数下的测试结果如图15所示。不同耦合因数下电磁推力实验结果与相应正比例拟合曲线的拟合优度2=0.993，实验结果表明电磁推力与耦合因数成正比关系，验证了新型单元电机模型理论的正确性。

图15 电磁推力随耦合因数变化的实验结果

6 结论

本文通过引入虚拟次级并结合耦合因数推导得到了分段LP-DSLIM单元电机新型数学模型，基于新型单元电机模型分别建立了串联供电和并联供电的分段LP-DSLIM系统模型。有限元计算和实验结果验证了新型单元电机模型和分段LP-DSLIM系统模型的正确性。结论如下：

1）通过引入虚拟次级避免了次级侧参数变化带来的影响，能准确地描述次级磁链和次级电流。

2）单元电机的电磁推力和次级磁链均与耦合因数成正比。

3）新型单元电机模型能更准确地描述实际单元电机，以新型单元电机模型为模块，可灵活建立在串联和并联供电方式下的分段LP-DSLIM系统模型。

新型单元电机数学模型及分段LP-DSLIM系统模型为该类大功率电机系统的控制提供了一种有效路径。

[1]Bushway R R. Electromagnetic aircraft launch system development considerations[J]. IEEE Transactions on Magnetics, 2001, 37(1): 52-54.

[2]Yang Tong, Zhou Libin, Li Langru. Influence of design parameters on end effect in long primary double-sided linear induction motor[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 192-197.

[3]曹瑞武, 苏恩超, 张学. 轨道交通用次级分段型直线磁通切换永磁电机研究[J]. 电工技术学报, 2020, 35(5): 1001-1012. Cao Ruiwu, Su Enchao, Zhang Xue. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1001-1012.

[4]张志华, 史黎明, 李耀华. 栅格次级双边直线感应电机特性[J]. 电工技术学报, 2014, 29(3): 103-110. Zhang Zhihua, Shi Liming, Li Yaohua. Characteristics of double sided linear induction motors with ladder-slit type secondary[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 103-110.

[5]鲁军勇, 马伟明, 李朗如. 高速长初级直线感应电动机纵向边端效应研究[J]. 中国电机工程学报, 2008, 28(30): 73-78. Lu Junyong, Ma Weiming, Li Langru. Research on longitudinal end effect of high speed long primary double-sided linear induction motor[J]. Proceedings of the CSEE, 2008, 28(30): 73-78.

[6]孙兆龙, 马伟明, 鲁军勇, 等. 长初级双边直线感应电动机静态纵向边端效应及阻抗矩阵研究[J]. 中国电机工程学报, 2010, 30(18): 72-77. Sun Zhaolong, Ma Weiming, Lu Junyong. Research of static longitudinal end effect and impedance matrix for long primary double-sided linear induction motors[J]. Proceedings of the CSEE, 2010, 30(18): 72-77.

[7]杨通, 周理兵. 长初级双边直线感应电机纵向动态端部效应第一部分:气隙磁场[J]. 电机与控制学报, 2014, 18(4): 52-59. Yang Tong, Zhou Libing. Longitudinal dynamic end effect in long primary double-sided linear induction motor Part 1: airgap magnetic field[J]. Electric Machines and Control, 2014, 18(4): 52-59.

[8]杨通, 周理兵. 长初级双边直线感应电机纵向动态端部效应第二部分:性能计算[J]. 电机与控制学报, 2014, 18(8): 67-74. Yang Tong, Zhou Libing. Longitudinal dynamic end effect in long primary double-sided linear induction motor Part 2: performance calculation[J]. Electric Machines and Control, 2014, 18(8): 67-74.

[9]任晋旗, 李耀华, 王珂. 动态边端效应补偿的直线感应电机磁场定向控制[J]. 电工技术学报, 2007, 22(12): 61-65. Ren Jinqi, Li Yaohua, Wang Ke. Indirect field oriented control of linear induction with end effect compensation[J]. Transactions of China Electrotechnical Society, 2007, 22(12): 61-65.

[10]李卫超, 胡安, 马伟明, 等. 新型长定子直线感应电机闭环控制策略[J]. 中国电机工程学报, 2010, 030(z1): 226-231. Li Weichao, Hu An, Ma Weiming, et al. Control strategy of a novel double-sided long primary linear induction motor[J]. Proceedings of the CSEE, 2010, 30(z1): 226-231.

[11]王江波, 李耀华, 严陆光. 长初级双边直线电机高性能控制策略[J]. 电工技术学报, 2011, 26(5): 126-131. Wang Jiangbo, Li Yaohua, Yan Luguang, et al. High performance control strategy for long primary double sided linear motors[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 126-131.

[12]陈晓, 赵文祥, 吉敬华, 等. 考虑边端效应的双边直线永磁游标电机模型预测电流控制[J]. 电工技术学报, 2019, 34(1): 49-57. Chen Xiao, Zhao Wenxiang, Ji Jinghua, et al. Model predictive current control of double-side linear vernier permanent magnet machines considering end effect[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 49-57.

[13]许金, 马伟明, 鲁军勇, 等. 长定子直线感应电机饱和特性和非线性计算[J]. 电工技术学报, 2012, 27(9): 183-190. Xu Jin, Ma Weiming, Lu Junyong. Saturation characteristics analysis and nonlinear calculation methods of long-stator linear induction motors[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 183-190.

[14]张千, 刘慧娟, 马杰芳, 等. 考虑后退行波的长初级双边直线感应电机电磁性能计算[J]. 电工技术学报, 2020, 35(7): 1398-1409. Zhang Qian, Liu Huijuan, Ma Jiefang, et al. Calculation of electromagnetic performance for long primary double sided linear induction motors considering backward traveling wave[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1398-1409.

[15]王明杰, 徐伟, 杨存祥, 等. 基于精确子域模型的永磁直线同步电机空载磁场解析计算[J]. 电工技术学报, 2020, 35(5): 942-953.Wang Mingjie, Xu Wei, Yang Cunxiang, et al. Analytical calculation of no-load magnetic field in permanent magnet linear synchronous motors based on an accurate subdomain model[J]. Transactions of China Electrotechnical Society, 2020, 35(5):942-953.

[16]邸珺, 范瑜, 刘亚静. 基于等效次级的直线感应电机的电磁分析与参数辨识[J]. 电工技术学报, 2017, 32(11): 145-154. Di Jun, Fan Yu, Liu Yajing. Electromagnetic analysis and parameter estimation for the linear induction motor based on equivalent secondary[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 145-154.

[17]张明元, 马伟明, 何娜. 长初级直线电动机分段供电技术综述[J]. 中国电机工程学报, 2013, 33(27):96-104. Zhang Mingyuan, Ma Weiming, He Na. Application of block feeding methods in long primary linear motors[J]. Transactions of China Electrotechnical Society, 2013, 33(27): 96-104.

[18]马名中, 马伟明, 范慧丽, 等. 长初级直线感应电机分段供电切换暂态过程[J]. 电机与控制学报, 2015, 19(9): 1-7. Ma Mingzhong, Ma Weiming, Fan Huili, et al. Switch transient process of section powered long-primary linear induction motor[J]. Electric Machines and Control, 2015, 19(9): 1-7.

[19]Sun Xiao, Shi Liming, Zhang Zhihua, et al. Thrust control of double sided linear induction motor with segmented power supply[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4891-4900.

[20]龙遐令. 直线感应电动机的理论和电磁设计方法[M]. 北京: 科学出版社，2006.

[21]鲁军勇, 马伟明, 许金.高速长定子直线感应电动机的建模与仿真[J]. 中国电机工程学报, 2008, 28(27): 89-94. Lu Junyong, Ma Weiming, Xu Jin. Modeling and simulation of high speed long primary double-sided linear induction motor[J]. Proceedings of the CSEE, 2008, 28(27): 89-94.

[22]张明元, 马伟明, 徐兴华, 等. 一种考虑电流过零的直线电机分段供电策略[J]. 海军工程大学学报, 2019, 31(4): 11-16. Zhang Mingyuan, Ma Weiming, Xu Xinghua, et al. A block feeding strategy for linear motor considering switching at current-crossing point[J]. Journal of Naval University of Engineering, 2019, 31(4): 11-16.

[23]上官璇峰, 励庆孚, 袁世鹰. 多段初级永磁直线同步电动机驱动系统整体建模和仿真[J]. 电工技术学报, 2006, 21(3): 52-57. Shangguan Xuanfeng, Li Qingfu, Yuan Shiying. Integrated modeling and simulation of the systems driven by multi-segment primary permanent linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2006, 21(3): 52-57.

[24]上官璇峰, 励庆孚, 袁世鹰. 多段初级永磁直线同步电动机系统建模及制动仿真[J]. 西安交通大学学报, 2006, 40(6): 694-698. Shangguan Xuanfeng, Li Qingfu, Yuan Shiying. Modeling of the systems driven by multi-segment primary permanent magnet linear synchronous motor and the simulation of brake process[J]. Journal of Xi'an Jiaotong University, 2006, 40(6): 694-698.

[25]孙晓, 史黎明, 张志华, 等. 并联双边直线感应电机次级定向控制[J]. 中国电机工程学报, 2019, 39(4): 1181-1189. Sun Xiao, Shi Liming, Zhang Zhihua, et al. The secondary field oriented control of parallel connected double sided linear induction motor[J]. Proceedings of the CSEE, 2019, 39(4): 1181-1189.

[26]Sun Xiao, Shi Liming, Zhang Zhihua, et al. A novel field oriented control for parallel-connected double-sided LIM[C]//2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, 2016: 1894-1897.

Modeling and Analysis of Segmented Long Primary Double-Sided Linear Induction Motor

Zhang Mingyuan1,2Shi Liming1Guo Keyu1,2Yang Zeyu1Xu Fei1

（1. Key Laboratory of Power Electronics and Electric Drive Institute of Electrical Engineering Chinese Academy of Sciences Beijing 100190 China 2. University of Chinese Academy of Sciences Beijing 100049 China）

The segmented long primary double-sided linear induction motor (LP-DSLIM) system is composed of several segments of unit motors powered in series or in parallel. To accurately describe the state change of unit motor and the transient process when passing through segments during secondary motion, a new mathematical model of unit motor and a segmented LP-DSLIM system model are proposed in this paper. Firstly, the characteristics of the segmented LP-DSLIM system are analyzed. By introducing the virtual secondary board, the secondary coupling of each unit motor is extended to the same length as the primary, so that the primary and secondary of the unit motor are always fully coupled. Then, the actual secondary flux linkage and primary flux linkage are obtained by combining with the coupling factor. The new unit motor mathematical model is derived, and the segmented LP-DSLIM system model is established. Finally, the proposed new unit motor mathematic model and segmented LP-DSLIM system model are verified by FEM calculation and experiments.

Long primary double-sided linear induction motor, unit motor, mathematical model, virtual secondary board, coupling factor

TM359.4

10.19595/j.cnki.1000-6753.tces.201101

国家重点研发计划资助项目（2016YFB1200602-19）。

2020-08-30

2020-12-12

张明远 男，1995年生，博士研究生，研究方向为大功率电力电子变换技术与直线电机驱动控制。E-mail：myzhang@mail.iee.ac.cn

史黎明 男，1964年生，研究员，博士生导师，研究方向为特种电机和驱动控制、电能无线传输技术。E-mail：limings@mail.iee.ac.cn（通信作者）

（编辑 郭丽军）