基于贝叶斯网络时序模拟的气电耦合系统可靠性评估
2021-06-09杨晨曦高立艾唐巍
杨晨曦,高立艾,唐巍
(1.河北农业大学机电工程学院,河北 保定 071000;2.中国农业大学信息与电气工程学院,北京 100083)
能源是社会赖以生存和发展的根本,在确保我们使用能源持续性的同时,有效减少对环境的污染,是现今世界共同关注的热点。近些年来,社会生活生产对能源需求日益增加,面对人类社会能源的紧缺以及环境愈加恶化的双重压力,在现有能源结构格式上来提高能源的利用率,并加强对具有再生性的能源使用成为了研究界的一大热点。在这一背景下,充分对新型能源使用的综合系统应运而生。它可以有效调节不同的供能系统,使社会能源更加安全、灵活、可靠地供用。基于上述研究背景,目前最常见的是配电-天然气间系统的互联,天然气这种能源具有清洁高效的优点,所以在当今社会新能源领域内备受青睐。
当前,综合能源方面的研究处于起步阶段,例如文献[1]对电/气/热微型能源系统方面的研究。首先从研究方法上,从可靠性角度出发,相对以往传统的电力网系统,综合能源系统初步可理解为:以电力系统为主导,其他新兴尖端科技为辅助,并以可再生的能源作为首要的一次性能源。结合成一个复杂的多网络系统,与其他能源网络(如天然气网络)进行紧密相连,主要采用解析及蒙特卡洛方法对其进行分析。
文献[2]引入了能量枢纽的概念来描述分布式能源系统的多能量结合特性,并采用解析方法对包括储能在内的分布式能源系统的可靠性进行了评价。但是其计算量复杂,求解困难。文献[3]采用马尔科夫链蒙特卡罗方法对配电网下分布式集成能源系统的可靠性进行了评价,并对系统的可靠性指标进行了定量评价。缺点在于不能识别系统故障后薄弱的环节。其次,从研究内容上,文献[4-7]只分析了电力系统的可靠性。文献[8-10]只是对燃气系统的供能可靠性指标进行分析,并且没有识别薄弱环节,这些文献只是对单一系统进行研究。针对以上存在的问题,文中以气电耦合系统为对象来进行研究,基于贝叶斯网络对其可靠性方面进行分析,首先找出配电系统及天然气系统各网络中元件的逻辑关系,并对建立与其相应的贝叶斯网络。其次建立整个气电耦合互联系统贝叶斯网络,采用贝叶斯网络时序模拟算法对气电耦合系统进行可靠性研究,并对系统发生故障后,互联系统中所存在薄弱的环节进行识别,最后结合实际算例进行研究分析。
1 基于贝叶斯网络的天然气系统可靠性分析
1.1 贝叶斯网络逻辑关系
贝叶斯网络其基本理论从本质上来看就是概率分析的过程,是不确定性推理的有向无环图模型。利用这种关系性,可以利用数值推理(实质为一种联合概率分布形式)表达出来,如下式:
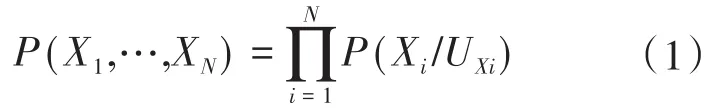
式中:X1~XN为节点的集合;UXi为 Xi中全部父节点的集合。
求和各个节点对它的父节点依赖的程度,利用条件概率表现出来。针对所研究的具体系统,把系统中线路、管道等元件以及负荷点均等效为节点,分析节点间的逻辑关系,以此构建出相应的贝叶斯网络,具体的逻辑关系可以划分为与、或、联合和因果关系,详见参考文献[11]。
1.2 天然气系统贝叶斯网络的建立
首先以11节点的天然气系统为例,NSG11拓扑结构图如图1所示。系统中包含2个气源点、8条输气管支路、2条燃气压缩驱动机支路、7个气负荷节点。其中4,5,11为商业用气;3,8,9为居民用气;10为加气站用气。
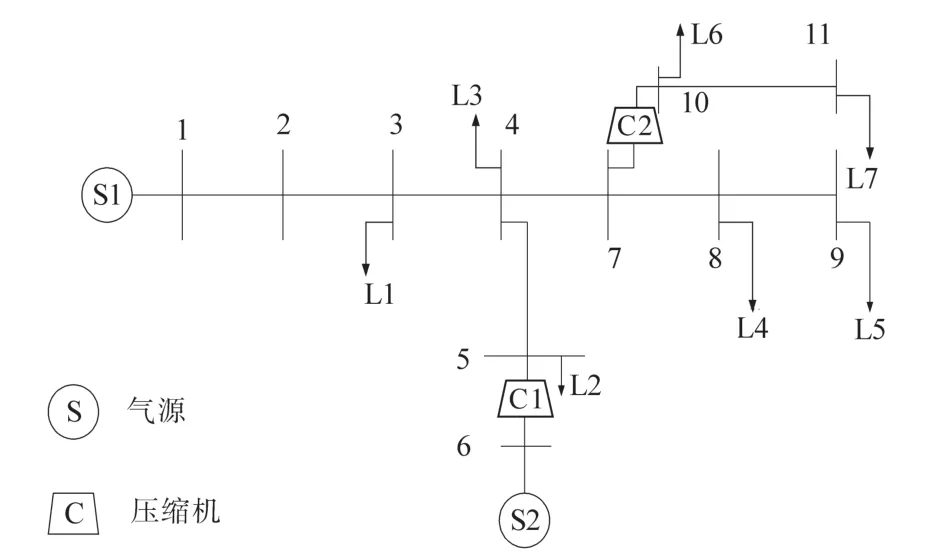
图1 NSG11拓扑结构图Fig.1 NSG11 topological diagram
图1中,天然气系统气源、压缩机及管道参数,各个负荷节点所需天然气及天然气源的供气量,天然气网络中负荷节点类型及其包含的用户数,均见参考文献[12]。
根据参数计算各个元件及管道故障率,气源作为贝叶斯网络的第1层节点,气管道及压缩机作为系统的第2层节点,各用气负荷作为第3层节点,然后分析系统元件之间以及元件与系统之间的逻辑关系,例如同一气源下各个管道与负荷间的与关系、不同气源及其所对应的管道对同一用气负荷的或关系、负荷与天然气系统之间因果关系等,最后建立与其相对应的贝叶斯网络,如图2所示。
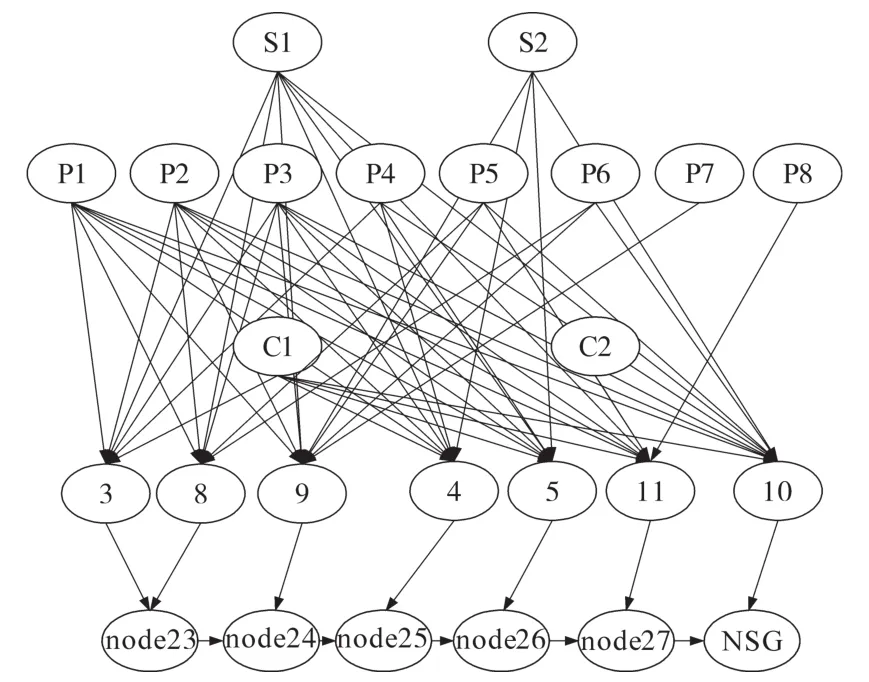
图2 天然气系统贝叶斯网络Fig.2 Natural gas system Bayesian network
1.3 算例分析及结论
文中采用美国匹兹堡大学的可视化GeNIe2.0软件平台提供的贝叶斯网络精准推理的算法,建立天然气系统贝叶斯网络,通过程序编写自动生成DSL格式的贝叶斯网络文件。将整个气电耦合系统主要接线上的每个元器件作为一个节点来写入贝叶斯网络结构中,由此计算出天然气系统的可靠性指标:失气负荷概率(loss of gas load proba⁃bility,LOGLP)和气量不足期望(expected gas not supplied,ENGS),如表1所示,其结果与文献[12]解析法的结果一致,验证了贝叶斯网络逻辑关系以及推理算法用于天然气系统的正确性和有效性。
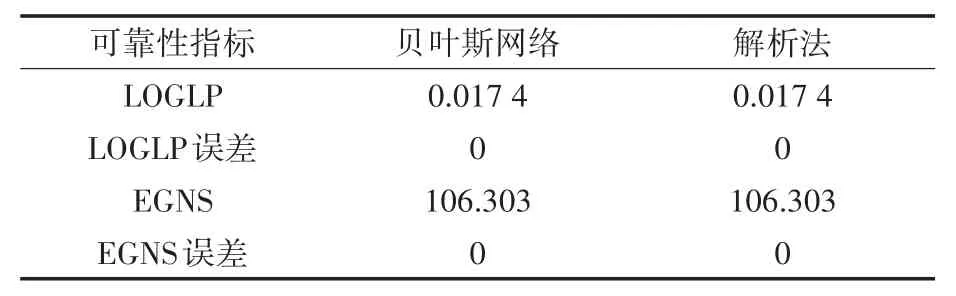
表1 可靠性指标对比Tab.1 Reliability index comparison
由此可见,分析系统间元件的逻辑关系并利用贝叶斯网络算法,所得出的结果精准,且计算精简。并且可以根据所搭建的贝叶斯网络结构来进行反推,识别系统中的薄弱环节,如图3所示。
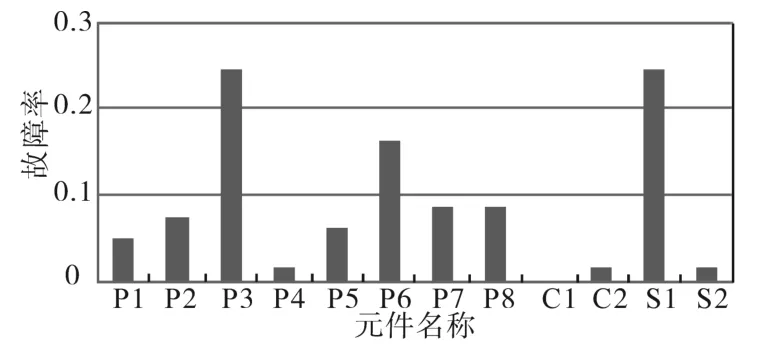
图3 各元件故障率Fig.3 The failure rate of each component
借助于贝叶斯网络诊断推理,可以求解出天然气系统发生故障时,系统中各个气源、管道、压缩机等元件所发生故障的概率,通过图3可知,气源S1、管道P3故障率最高,由此识别系统可靠性的薄弱环节,在制定系统检修计划时可以着重加强对可靠性较低的管道的保护,在实际运行中采取有效措施,例如缩减系统元件的修复时间或者减小故障次数,以提高各部件的可靠性从而提高系统整体的可靠性。
2 基于贝叶斯网络的气电耦合系统可靠性评估
2.1 气电耦合系统基本原理
气电耦合系统主要由一个配电系统和一个天然气供气网组成,通过电转气(power to gas,P2G)系统和燃气轮机进行耦合,系统中的燃气轮机和P2G作为系统间的转换装置是其关键的部分,就是将燃气轮机发电系统接入电力系统以作为分布式电源,运用天然气燃烧来使同步发电机发电,在配电系统这一侧可以看作是一个电源,为配电系统部分用电用户供电。P2G系统对于天然气系统具有气源特性,利用水和CO2将电能转换为化学能的技术概念,为天然气系统中部分负荷供气。利用耦合装置将其连接起来,从而形成互联系统。
2.2 基于时序模拟气电耦合系统可靠性算法
精确推理算法不能计算和频率相关的指标,因此本小节结合上节所建立的天然气系统贝叶斯网络,采用基于贝叶斯网络时序模拟算法,对气电耦合系统进行可靠性方面的分析研究,运用C#.net2015编程,求出整体系统的可靠性指标。由于篇幅有限,仅截取系统部分故障累计时间的程序,如图4所示,其具体操作流程如下。

图4 系统部分程序Fig.4 Part program of system
首先初始化数据,输入气电耦合系统中各元件的参数。由于全年共有8 760 h,气电耦合系统各个电源以及负荷点的功率是随着时间变化的,在进行时序模拟时,根据时变曲线将全年划分成8 760个时间段,设定i=8 760。其次,计算出柴油机组所发出的功率PDG以及风电机组发出功率PWG,并考虑储能装置的加入,根据功率间的关系确定系统之间的潮流。然后对互联系统中各部分元件状态的持续时间进行比较,选取状态持续的最小时段作为最小的持续时间。在最小的持续时间段里面,根据第1节所提到的贝叶斯网络中的逻辑关系进行时序模拟分析,之后确定气电耦合系统的负荷运行状态,累计出各部分元器件的故障时间、系统发生故障时间、停电总时间、失气总时间等,利用这些数据分析得出系统的可靠性指标,最后输出数据,其具体的流程图如图5所示。

图5 程序流程图Fig.5 Program flow chart
3 算例分析
以IEEE-RBTS-BUS-6系统主馈线F4配电网和比利时11节点天然气系统为基础,利用燃气轮机和P2G装置耦合构造出一个气-电耦合系统来进行分析,如图6所示。
图6所示的气电耦合综合系统共包含53条配电线路、23个负荷点、8条输气管支路、2条燃气压缩驱动机支路和7个气负荷点,其中4,5,11为商业用气负荷节点,3,8,9为居民使用负荷节点,10为加气站用气负荷节点,含有两气源点。天然气网络中的负荷数据、管道参数和压缩机参数详见参考文献[12]。
图6中天然气节点5通过P2G装置与配电系统相连,节点11经过燃气轮机接入配电系统。根据所给参数运算分析得出各部分元器件、管道、线路的故障发生率,然后分析系统各部分元件之间以及元件与整体系统之间的逻辑关系,最后建立相应的气电耦合能源系统的贝叶斯网络,如图7所示。

图6 IEEE-RBTSBUS-6系统主馈线F4配电网和11节点天然气系统图Fig.6 IEEE-RBTSBUS-6 system main feeder F4 distribution network and 11⁃node natural gas system diagram
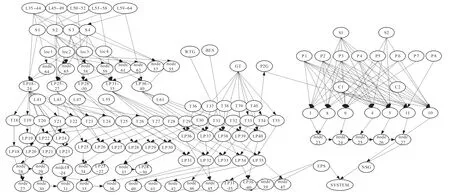
图7 气电耦合综合能源系统贝叶斯网络Fig.7 Gas-electric coupled integrated energy system Bayesian network
通过贝叶斯网络时序模拟推理算法分别得出电力系统和天然气系统在单一运行模式和互联模式下的可靠性方面的指标,如表2所示。
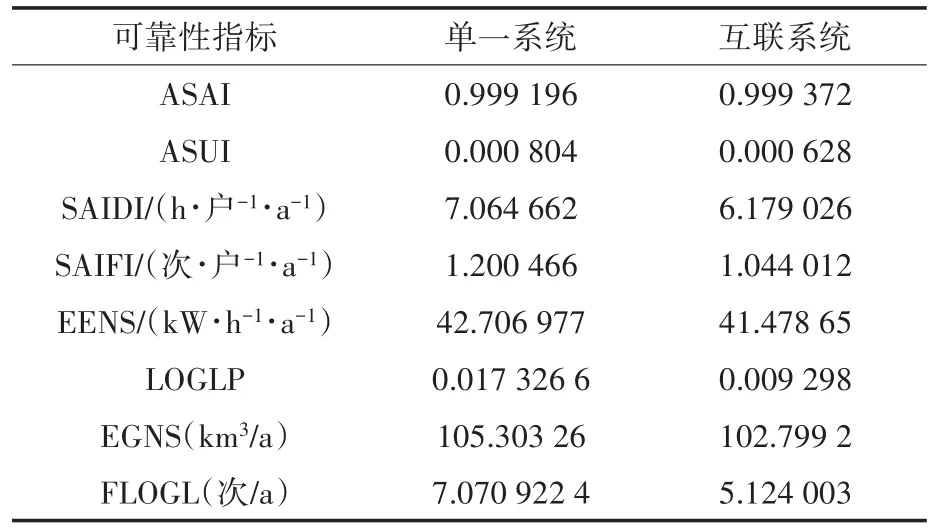
表2 可靠性指标对比Tab.2 Reliability index comparison
表2中对气电耦合系统所涉及到的可靠性指标为:系统中平均供电的可使用率(average ser⁃vice availability index,ASAI)、系统的平均供电的不可使用率(average service unavailability index,ASUI)、系统内部平均停电持续的时间(system av⁃erage interruption duration index,SAIDI)、系统内部平均停电的频率(system average interruption frequency index,SAIFI)、系统内部缺失电量的期望(expected energy not supplied,EENS)。其具体的计算公式可详见参考文献[12-14]。
通过表2可靠性指标的对比,可以发现单一的电力系统及天然气系统不论从系统可靠性还是各类负荷点的可靠性,都没有整体气电耦合综合能源系统的可靠性水平高。
根据贝叶斯网络诊断推理,求解气电耦合综合能源系统故障时的各个元件的故障概率,识别系统可靠性的薄弱环节,如图8所示。
通过图8,可以发现在气电耦合系统中,P2G转换装置以及燃气轮机在耦合系统中对可靠性的影响最高,在今后构建耦合系统时,应加强对系统之间耦合装置的保护或者选用可靠性较高的耦合元件。除耦合元件外,配电网线路L35-44,L53-58及天然气管道P5对综合系统可靠性影响较大,因为L35-44,L53-58及P5是配电系统及天然气系统主要线路和主管道,连接元件及负荷较多,所以应加强对这些主要线路及管道加强保护。在系统故障时,为维修工人提供检修维护的方向及目标,并提供极具参考价值的信息。
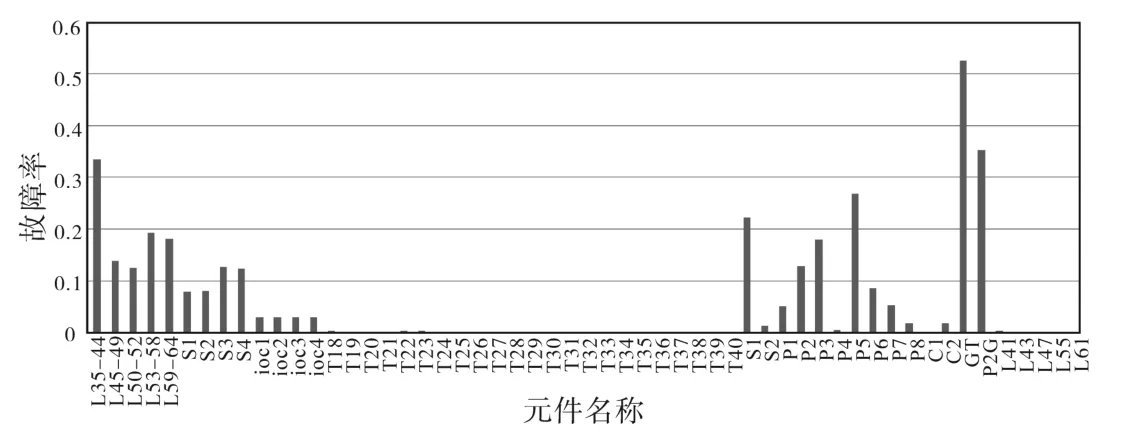
图8 气电耦合综合能源系统在系统故障时各元件故障率Fig.8 Failure rate of components in the integrated energy system with gas-electric coupling during system failure
4 结论
本文针对气电耦合综合能源系统,利用贝叶斯网络时序模拟的算法对其进行可靠性的研究与分析,结论如下:
1)相对于解析及蒙特卡洛法,文中所建立的贝叶斯网络能清晰的表明系统内元件的逻辑关系,结果正确有效。
2)对比分析不同模式下的可靠性指标,可以发现单一的配电系统及天然气系统不论从系统可靠性还是各个负荷点的可靠性都没有整个气电耦合综合能源系统的可靠性水平高。
3)依据贝叶斯网络诊断推理,可以识别系统可靠性的薄弱环节,为建设综合能源系统提供可靠依据以及为系统检修维护提供有价值的参考信息和方向。
