基于Popov理论的微电网逆变器控制策略研究

师洪涛，蒋中南，张巍巍 ，王福星，石宽，李一帆

（1.北方民族大学电气信息工程学院，宁夏 银川 750021；2.天津电气科学研究院有限公司，天津 300180）

微电网凭借可更加充分利用可再生能源（风能、太阳能、生物能等）、运行方式灵活等优点，日益得到人们的重视，得到广泛的研究和使用[1]。

微电网是一种小型分布式电力系统[2-3]，在一定区域内利用风力发电、光伏电板等分布式电源，根据用户需求提供电能。微电网既可以孤岛模式运行，也可并网运行[4-5]。

在孤岛微电网中，微电网的电能质量与逆变器的控制性能有关[6-7]，逆变器的控制性能容易受到微电网中负载或者其它电力电子变流器的影响。因此，在不同的工况下，会出现微电网电压偏差、频率偏差、三相电压不平衡、谐波污染等电能质量问题。

对于微电网电能质量问题的治理，可以分为设置电能质量治理装置和在电力电子变流器中设计控制策略[8]。对于电能质量治理装置，需要额外设置在微电网中，增加了成本。对于电力电子变流器控制策略，鲁棒控制被用于微电网系统电能质量[9-10]治理。然而，高阶系统需要更高阶的鲁棒控制器，以确保其与先进的数字信号处理器（digital signal processor，DSP）系统一起运行。二次控制被提出用于实现微电网频率与电压等电能质量问题的无差控制[11-12]。二次控制根据微电网逆变器所处的某特定的工况对逆变器的性能进行调节与控制，当需要调节的参数较多时，需要设计较复杂的控制系统[13-14]。上述控制策略，可以保证微电网电能质量，但在复杂的工况下，控制策略复杂，系统稳定性差且跟踪性能受到影响。

自适应控制[15-16]于1950年末在美国麻省理工学院（MIT）的实验室被提出[17-18]。模型参考自适应控制中，MIT方案只能调整系统中局部参数并且不能保证系统的稳定性。Lyapunov理论中[15]，函数V难以确定，且不唯一。而Popov理论中的普适性方法[16]，改善了Lyapunov理论中带来的问题。

因此，针对以上不足，在逆变器传统下垂控制的基础上，提出了一种基于Popov理论的微电网逆变器电能质量控制策略。该策略建立了微电网电压控制的参考模型、Popov控制器和自适应机构。以调整微电网逆变器端口电压为目的，自适应调整Popov控制器参数，使得逆变器实际输出电压对理想电压具有良好的跟踪性。

1 孤岛微电网不同工况下的电能质量分析

1.1 孤岛微电网的结构

在孤岛微电网中，网内负载的用电情况随着不同时间段需求波动，柴油发电机与微型燃气轮机等化石燃料发电保证了基础与应急供电，可再生能源分布式发电装置（风力发电机、光伏电池板等）在不同时间段根据需求进行缺口补充及储能充电，通过合理规划和需求预测来满足负载需求，同时降低运营成本。

如图1所示，在孤岛运行状况下，微电网通过公共连接节点（point of common coupling，PCC）断开与大电网的连接，通过微电网内的发电装置或储能设备维持电网的运行。微电网通过控制储能充放电以调节可再生能源间歇性问题，并利用当地风能、太阳能进行发电，以确保满足不同时间段的负载需求[19]。

图1 微电网结构示意图Fig.1 Schematic diagram of island microgrid structure

在孤岛微电网运行中，通过微电网内的发电设备与储能设备维持电网的运行。一般情况下，由储能设备组成系统，以此平衡分布式发电装置的发电与负荷的用电，而风机、光伏、燃料电池等供电装置都需要通过电力电子变流器并网[20]。通过提高微电网中逆变器的控制性能，调整公共连接点的电压，以保证微电网中的电能质量。

1.2 微电网逆变器的结构与控制方式

微电网逆变器系统，采用三相三线两电平全桥拓扑，逆变器输出使用LC滤波器进行滤波，如图2所示。

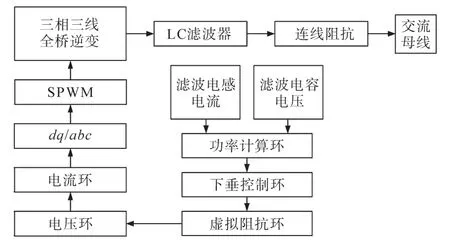
图2 微电网逆变器结构Fig.2 Microgrid inverter structure

微电网逆变器系统的控制电路部分有功率外环、电压环和电流环[21-22]。功率环作为整个系统的外环，通过采样逆变器自身的输出电压和输出电流计算逆变器输出的有功功率P和无功功率Q，再根据P—f和Q—U的下垂控制方程，给出系统稳定工作时的电压幅值和频率参考。下垂控制方程如下[21]：

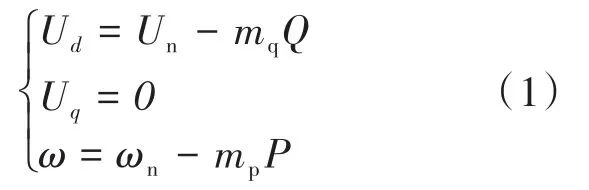
式中：mp，mq分别为电压和频率的下垂系数；Ud为输出电压的d轴参考电压；Un为逆变器额定输出电压值；Uq为输出电压的q轴参考电压，设置为0；ω为逆变器输出电压频率参考值；ωn为额定角频率。

在传统控制器中加入虚拟电感，使微电网逆变器系统的输出阻抗感性增强。提高了有功、无功的解耦控制精度，同时还可抑制并联逆变器间的无功环流[23-24]。另外，虚拟电阻的加入，增加了系统的阻尼，能有效抑制系统振荡。在dq坐标系下实现虚拟阻抗如下：

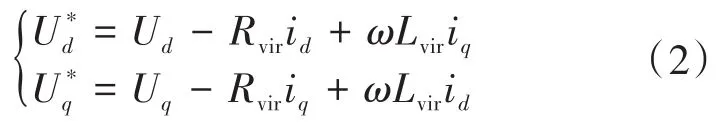
电压环在dq旋转坐标系下采用PI调节器，保证逆变器的输出电压能够快速准确地跟踪参考电压，维持输出电压稳定；电流环作为系统内环，同样采用PI调节器，控制流入滤波电感的电流，使其能准确跟踪上电压环的输出，进一步提高了系统整体的动态响应性能。

1.3 微电网中电能质量问题

微电网中发电装置的输出功率受环境的影响，具有波动性与间歇性。波动的功率注入至微电网中，微电网中功率发生波动，式（1）中的电压与频率受有功功率P和无功功率Q影响，进而导致微电网电压幅值与频率发生偏移。

微电网一般建设在配电网的末端，其中较多的分布式发电设备采用单相电力电子变流器并入微电网，用户负荷也大多为单相或三相不平衡设备。当微电网中连接了不平衡负载或单相分布式发电装置时，PCC电压可以表示为[25]

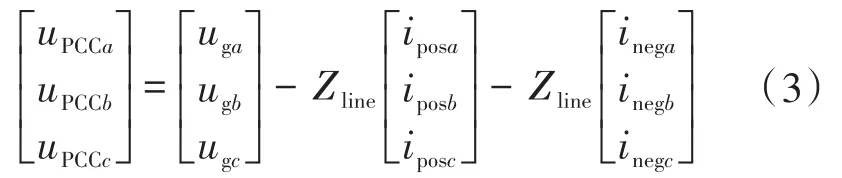
式中：uPCCa，uPCCb，uPCCc为 PCC电压；uga，ugb，ugc为三相实际电压；Zline为连线阻抗；iposa，iposb，iposc为正序三相电流；inega，inegb，inegc为负序三相电流。

由此可知，三相不平衡电流流入微电网，线路阻抗Zline两端存在负序电压降，PCC中存在一个负序电压，微电网电压处于不平衡状态。

微电网中的分布式发电系统及部分用户负荷均采用电力电子变流器通过一级或者多级变换接入至母线中，相对于传统电网，较高比例的电力电子设备带来的谐波问题更为突出，谐波的频带更宽，谐波分布更复杂。以非线性负载为例，当其接入微电网系统时，PCC电压表示为

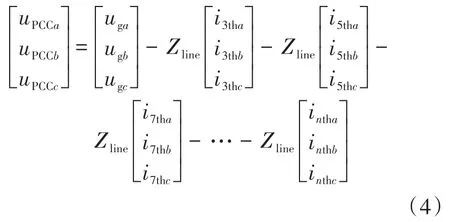
式中：intha，inthb，inthc为各次谐波电流。

此时，各次谐波电流进入微电网，产生谐波压降，微电网中出现谐波污染问题。

微电网发生电能质量问题时，在一定程度上会影响设备的正常运行。当电能质量问题严重时还会造成大规模的停电事故，因此对微电网进行有效的电能质量治理尤为重要。

2 提出的微电网逆变器Popov自适应控制策略

2.1 模型参考自适应控制的结构

用超稳定性理论进行模型参考自适应控制（model reference adaptive control，MRAC）设计中，线性前向回路主要为参考模型，非线性的反馈回路由具有时变非线性的被控对象和比例积分控制器共同组成[26]，如图3所示。

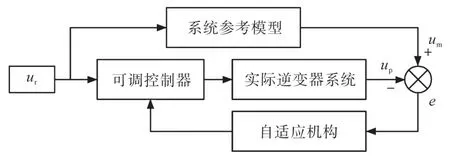
图3 MRAC系统框图Fig.3 MRAC system block diagram

图3中，ur为输入电压，e为广义误差，um和up分别为参考模型输出电压和实际输出电压。

2.2 自适应控制器设计

研究对象采用孤岛微电网逆变器系统。对传统下垂控制下的孤岛微电网逆变器系统进行建模，得到系统参考模型。根据模型参考自适应控制[26]，定义广义误差：

式中：um(t)为参考模型输出电压：up(t)为微电网逆变器实际输出电压。

自适应控制的最终目的是：

微电网逆变器系统状态方程为

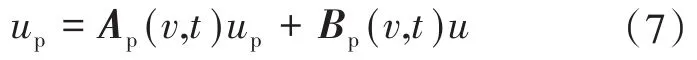
参考模型状态方程为

式中：Ap(v,t)，Bp(v,t)为实际逆变器系统中可调控制器的系数矩阵；Am，Bm为参考模型中理想状态下的系数矩阵；u为实际逆变器系统参考电压；v为系数矩阵中可调单位元素。

根据Popov理论，设计模型参考自适应控制器需要满足[27-28]：

1）线性前向部分传递函数：

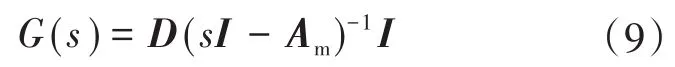
其中前向部分中，传递函数G（s）必定为严格正实；

2）非线性等效反馈部分，要求满足Popov理论中的积分不等式：

式中：n为输入与输出内积的积分；τ2为任意有限正数[27]。

为满足前向通道的正实性，需要将设定的正实性补偿器D（s）串入前向方块中。当参考模型趋于稳定后，存在正定堆成矩阵P和Q，使得：

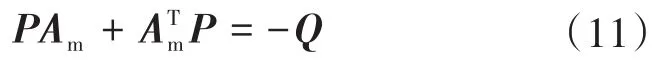
取PI=D，由此前向部分的传递函数是严格正实的。

在反馈部分，采用比例积分调节，如下式：

其中，As(v,t)为控制回路1表达式，由积分部分T1(v,t,τ )、比例部分 T2(v,t)与调整初值 As0三部分共同组成；Bs(v,t)为控制回路2表达式，由积分部分φ1(v,t,τ)、比例部分φ2(v,t)与调整初值Bs0三部分共同组成；v,t,τ均为可调量。

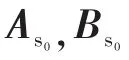
将v(τ)=r(t)和up自适应规律代入下式：

式中：xp为微电网逆变器系统的实际输入量；γ2为有限正数。

最终分解为

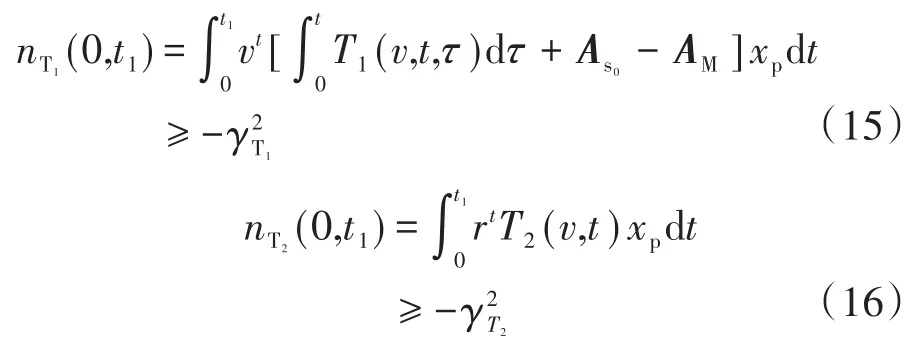
要求式（15）、式（16）满足Popov积分不等式（式（10））。

如图4所示，首先通过建立匹配逆变器模型的参考模型，跟踪模型输出的误差，将获得的结果发送给自适应机构。系统通过计算参考模型与实际逆变器之间的误差，在自适应机制中计算并生成实际逆变器中各参数的调节量，形成自适应律。该系统可以灵活地更改控制系统的参数，以保证逆变器的端口电压维持在额定值，保证了微电网的电能质量。

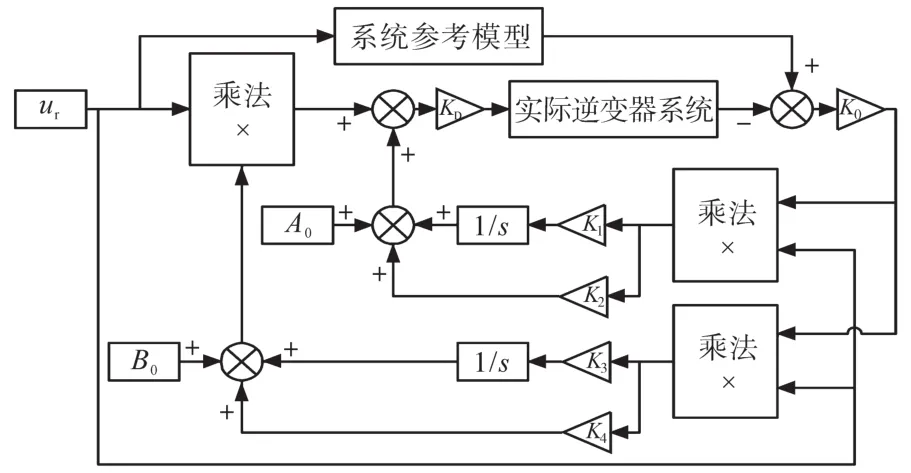
图4 系统控制框图Fig.4 System control block diagram

3 仿真验证

为验证文中提出的微电网逆变器Popov自适应控制策略的有效性，在Matlab中搭建了用于微电网的电压控制的逆变器的仿真模型。微电网逆变器的一些主要参数为：额定功率5 kW，额定输出电压220 V，额定频率50 Hz，开关频率10 kHz，输出滤波电感0.3 mH，滤波电容50 μF，有功功率下垂系数5e-4 V/var，无功功率下垂系数3e-5 rad·s-1/W。

分别选择阻感性负载、三相不平衡负载、非线性负载在传统控制策略和自适应控制策略下进行对比实验。负载参数为：阻感性三相平衡负载22.5 Ω+12.5 mH，三相不平衡负载10.5/15.5/22.5 Ω+12.5 mH，不控整流负载并联电容1 500 μF，不控整流负载并联电阻10.5 Ω。

3.1 逆变器在传统下垂控制下运行

逆变器带有三相对称的阻感性负载运行，图5所示为逆变器端口的电压波形。从图中可以看出，逆变器的三相电压为三相对称的正弦波，逆变器的电压控制性能良好。

在逆变器运行8 s时，在逆变器的输出端口上再并入一组三相平衡的阻感性负载，从图5中可以看出，逆变器的输出电压的幅值略有降低，产生了一定的电压偏差。

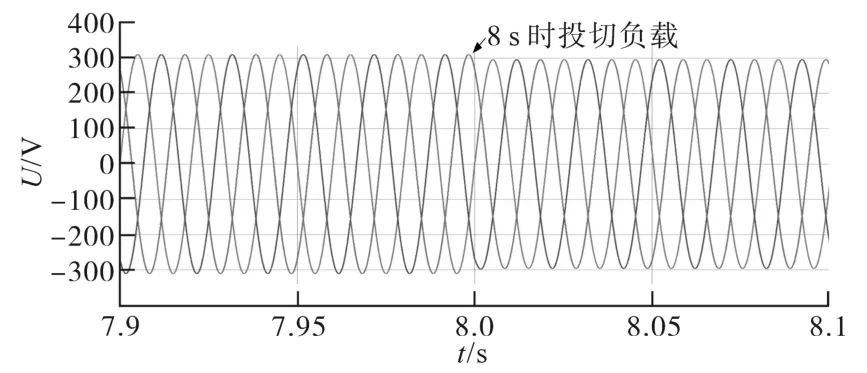
图5 传统控制下孤岛微电网母线电压波形图（电压偏差）Fig.5 Inverter output voltage waveform under traditional control（voltage deviation）

如图6所示，逆变器带有三相平衡负载运行，在8 s时，输出端口并入一组三相不平衡的阻感性负载。从图6可以看出，当三相不平衡负载切入至系统中后，逆变器的输出电流变得三相不平衡，即逆变器开始为负载提供三相不平衡的电流，其中包含较多的负序分量，此时，逆变器的输出电压也受到负序电流的影响，三相电压变得不平衡。

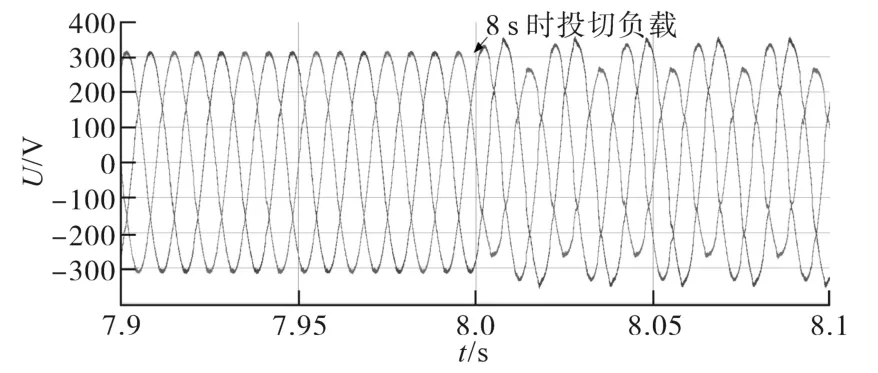
图6 传统控制下孤岛微电网母线电压波形图（三相不平衡负载）Fig.6 Inverter output voltage waveform under traditional control（three-phase unbalanced load）

图7所示为逆变器在带三相平衡的阻感负载的情况下，在8 s时切入一组三相的非线性负载，负载为采用电容滤波的三相不控整流器，直流侧的负载为5 Ω电阻。如图7所示，当非线性负载切入至系统中时，逆变器除了为负载提供基波电流外，还有大量的非线性电流，在这种情况下，逆变器的输出电压也受到影响，电压开始畸变，导致线性的负载中也产生谐波电流。

图7 传统控制下孤岛微电网母线电压波形图（非线性负载）Fig.7 Inverter output voltage waveform under traditional control（non-linear load）

图8所示为逆变器在带三相平衡的阻感负载的情况下，在8 s时切入三相不平衡负载与非线性负载，在这种情况下，逆变器的输出电流中，既包含负序分量，又包含谐波分量，同时，逆变器的输出电压受到较大的影响，也发生了三相不对称与谐波畸变。

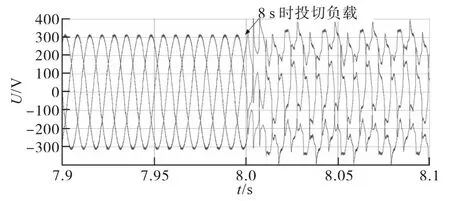
图8 传统控制下孤岛微电网母线电压波形图（三相不平衡负载+非线性负载）Fig.8 Inverter output voltage waveform under traditional control（three-phase unbalanced load+non-linear load）

3.2 逆变器在文中提出的自适应控制策略下运行

在逆变器中设置所提出的自适应控制策略，首先，逆变器带有三相平衡的阻感性负载运行。图9为自适应控制下孤岛微电网母线电压波形图。从图9中看出，逆变器的三相电压对称，三相电流对称，逆变器的控制性能良好。

图9 自适应控制下孤岛微电网母线电压波形图（电压偏差）Fig.9 Inverter output voltage waveform diagram under adaptive control（voltage deviation）

在逆变器运行8 s时，在系统中切入一组三相对称的阻感负载，在自适应控制器的作用下，逆变器的输出电压的幅值经过一定时间的调整后，又重新恢复到额定值，电压偏差几乎为零。

如图10所示，逆变器首先带有一组三相平衡的阻感负载运行，在8 s时逆变器系统中切入三相不平衡的阻感性负载，负载的数值与前文的传统下垂策略的实验中一致。在三相不平衡的负载切入至系统后，逆变器的输出电流受负载影响出现三相不平衡现象，即逆变器开始为三相不平衡的负载提供负序电流。然而，逆变器的三相电压经过短暂的调整后，仍然保持三相平衡，且幅值不变，维持为额定值。

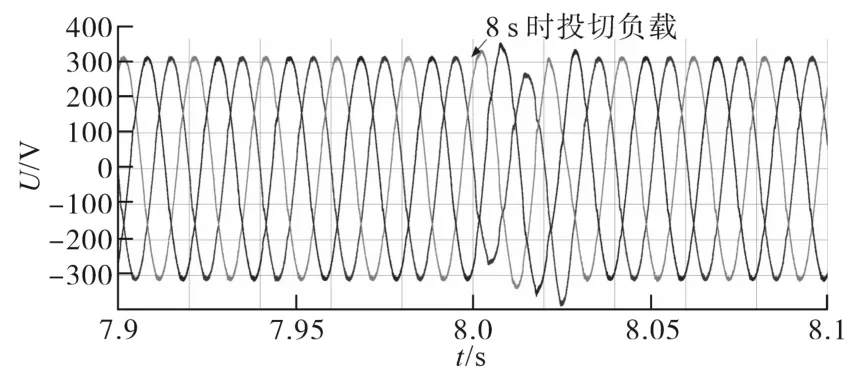
图10 自适应控制下孤岛微电网母线电压波形图（三相不平衡负载）Fig.10 Inverter output voltage waveform diagram under adaptive control（three-phase unbalanced load）

为了验证逆变器在非线性负载下的性能，如图11所示，在8 s时，在系统中切入一组三相不控整流器负载，逆变器的输出电流中包含较多的谐波电流分量，此时逆变器的电压经过短暂的调整后，能够维持三相正弦波形。

图11 自适应控制下孤岛微电网母线电压波形图（非线性负载）Fig.11 Inverter output voltage waveform diagram under adaptive control（non-linear load）

如图12所示，逆变器初始带有一组三相平衡的阻抗负载，在8 s时对系统投入一组三相不平衡负载与一组非线性负载，从图中可以看出，逆变器的输出电流三相不平衡，且发生谐波畸变。经过一段时间的调整，逆变器的输出电压仍能保持三相平衡且为正弦波，其幅值保持不变，电压偏差几乎为零。逆变器在复杂工况下的电压控制性能仍然良好。

图12 自适应控制下孤岛微电网母线电压波形图（三相不平衡负载+非线性负载）Fig.12 Inverter output voltage waveform diagram under adaptive control（three-phase unbalanced load+non-linear load）

4 结论

基于Popov超稳定性理论设计的微电网逆变器自适应控制策略，利用超稳定性理论推导自适应率，设计Popov控制器，使逆变器实际输出电压跟随理想电压，减少误差。在微电网逆变器系统运行过程中，实时对微电网中的电能质量问题产生响应，及时、稳定、精准地进行控制，保证了微电网逆变器系统较好的电能质量，是一种较实用的电能质量控制策略。