考虑需求响应和电动汽车负荷路-电耦合特性的配电网可靠性评估

林铭蓉，胡志坚，高明鑫，陈锦鹏

(武汉大学电气与自动化学院，武汉市 430072)

0 引 言

近年来，全球对于环境污染及能源匮乏等问题的关注度日益增加，电动汽车(electric vehicle，EV)因其绿色、环保的优势被大量接入电网[1]。电动汽车作为路-电两网的衔接者加入以后，改变了原本的负荷曲线，给配电网的可靠性带来负面影响。城市交通系统和配电系统息息相关，电动汽车作为电力网负荷终端，其时空分布受路网约束[2]。因此考虑路-电耦合能更精确地预测电动汽车时空负荷及其对配电网可靠性的影响。

准确预测电动汽车充电负荷是配电网安全运行的重要基础。当前，对于电动汽车充电负荷预测主要基于排队论、出行链、停车概率等[3-4]。文献[5]基于出行链，模拟每辆电动汽车一天内的行驶特性，获取电动汽车充电频率，但缺少对用户充电决策模糊性的考虑。文献[6]以停车概率预测负荷空间分布，以扩大范围的模糊函数确定充电模式，能够较好模拟用户对充电模式的差异性选择。文献[7]基于模糊理论，建立了考虑充电设施充裕度的出行需求与充电需求模型。但以上文献均未考虑与配电网之间的耦合，预测缺乏实用性。文献[8]通过对单体电动汽车负荷建模，运用交通起止点分析法模拟出行路径，建立各类电动汽车充电负荷模型。文献[9]依据车流量确定出行需求，建立山地城市的电动汽车负荷模型，但需要对每日车流量进行监控，数据收集时间长。

国内外学者对于含电动汽车的配网可靠性评估主要分为两个阶段。一是从电动汽车数量、接入位置、充电模式等方面分析EV接入对于配网可靠性的影响[10-11]。文献[12]考虑电动汽车与电网互动(vehicle-to-grid,V2G)技术，对含电动汽车的配电网可靠性进行评估。但文献[10-12]均设定电动汽车于某一固定点接入电网，未考虑电动汽车作为移动式负荷，空间位置上的随机性。二是在第一阶段的基础上研究基于交通网约束的含EV的配网可靠性评估。如文献[13]以全轨迹空间状态量描述私家车充电负荷的时空分布，基于最优负荷削减策略进行含分布式电源(distributed generation，DG)的可靠性评估。但现有研究均未考虑路-电耦合特性的EV负荷及其参与需求响应对配网可靠性的影响。

本文首先给出路-电耦合的电动汽车时空负荷预测整体框架；接着给出路网模型和包含出行起止点、路径选择、充电需求的用户模型；提出考虑需求响应(demand response,DR)的充电需求补充模型、电动汽车充电负荷时空预测模型以及基于双向层级结构的可靠性评估方法。最后，以某区域路网和配电网为例，模拟不同典型日下负荷的时空分布，并就各种场景下配电网的可靠性指标变化进行分析。本文提出的路-电耦合电动汽车充电负荷预测方法，既考虑到两网耦合，又能较好模拟出行需求。

1 路-电耦合模式结构及时空负荷预测框架

本文建立的电动汽车路-电耦合模式结构及时空负荷预测框架如图1所示。城市交通网状况与电网运行状况密不可分。城市交通网道路拥挤程度、通行能力会影响车主出行路径、行驶时间，继而改变电动汽车充电地点及充电时间，改变配电网负荷时空分布，影响配电网可靠性[14]。配电网为维持自身安全可靠运行，基于电价机制、奖惩机制与电动汽车进行互动，调控电动汽车接入电网的时间，改变车主充电意愿，影响车主计划的出行路径，反映在各道路车流量的变化情况上。

图1 路-电耦合模式结构及时空负荷预测框架 Fig.1 Structure chart of road-electricity coupling model and space-time load forecasting framework

首先，根据路网拓扑结构、道路等级、红绿灯及各功能区域分布情况建立路网模型。接着根据路网模型抽取出行链，运用基于Logit流量延误函数的改进Flody算法选择行驶路径，采用模糊理论确定用户充电意愿，判断是否参加需求响应，形成用户模型。结合路网模型及用户模型生成当前位置、初始电量、上下班时间、休闲时长及各关键时间节点，即每辆电动汽车的状态参数，继而获得电动汽车时空负荷模型，耦合至配电网，获得配网模型。最后，基于双向层级结构进行可靠性评估。

2 路网模型及用户模型

2.1 交通拓扑矩阵

假定道路均为双向，获取任意两点间距离D(i,j)，形成交通拓扑矩阵D。D(i,j)的赋值规则如下：

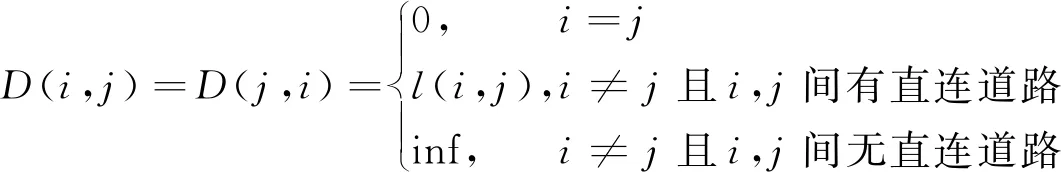
(1)

式中：l(i,j)表示i,j两点间的道路长度；inf表示i,j两点间不存在直接连通的道路。

2.2 出行起点及目的

出行链是通过模拟人的活动目的，形成按时间顺序排列的地点闭合连接链，可以刻画车主一天内的活动轨迹，获取始发地、中转地，使得模拟车辆转移时更接近车主实际决策[15-17]。出行链具有空间属性和时间属性双重特性，具体形式如表1所示。

表1 出行链结构Table 1 Travel chain structure

2.3 路径选择

在城市化快节奏生活观念影响下，车主通常倾向于选择耗时最短的路径。本文根据交通网拓扑模型，采用基于Logit流量延误函数[18]的改进Flody算法优化路径选择。算法的基本步骤如下：

步骤1：基于Logit流量延误函数获得各路网节点通行时间矩阵T，具体步骤参考文献[18]，在此不再赘述。

步骤2：基于步骤1考虑道路实际交通状况，采用改进的Flody算法，将权值由道路长度改进为道路通行时间，选取耗时最短的出行路径，得各交通起止点(origin destination，OD)间的最短通行时间矩阵Ts、路径矩阵B。

若i,j两点间耗时最短的出行路径由p条直连道路组成，则从i点出发到达j点的行驶里程、行驶时间如下：

(2)

ΔTij=Ts(i,j)

(3)

式中：Δdij、ΔTij分别为i点出发到达j点的行驶里程、行驶时间；Dq为i,j两点间第q条直连道路长度。

2.4 电量消耗

假设随电动汽车行驶里程的增大，耗电量线性增加，从地点i出发，到达目的地j，EV的荷电量由式(4)决定[19]：

(4)

2.5 充电需求

用户充电行为不能简单地归纳为在“到达目的地充电”和“到达目的地且无法满足下一次行程充电”两种情况下满足0-1分布。本文由用户主观意愿出发，当荷电量与下次行程所需电量相比越不足，用户充电需求越迫切，引入“电量充裕度”[7]来表征当前电量对于下次出行需求所需电量的充裕度：

(5)

式中：PA为电量充裕度指标；di+1为下次出行的行驶里程。

参考文献[7]，采用降岭型分布的隶属函数来描述用户充电决策的个体差异，其数学表达式如下：

(6)

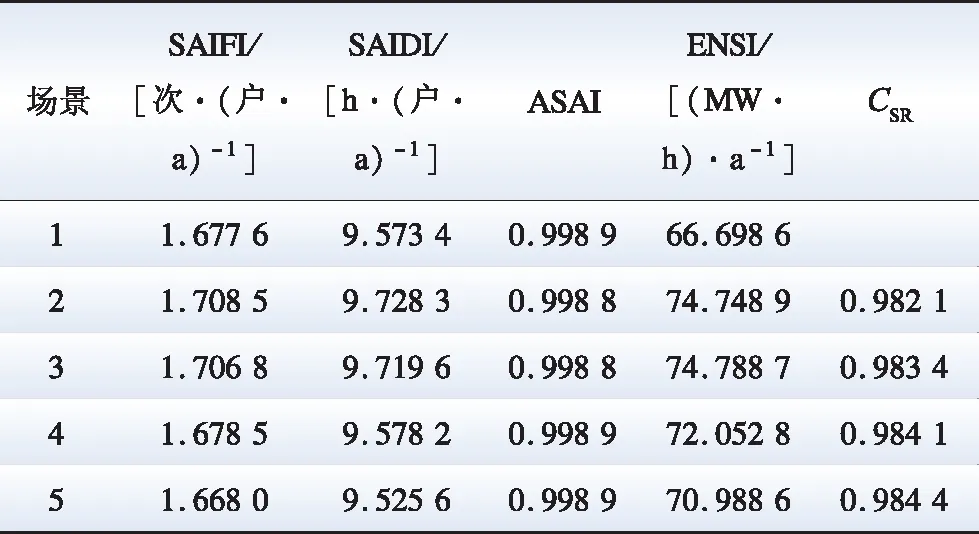
式中：l、u分别表示上下限函数。当PA

确定有充电需求后，进行充电模式选择。快充降低电池的使用寿命，从用户偏爱度出发，优先采用慢充模式，首先计算慢充所需时间：

(7)

式中:Tslow、Pslow分别为慢充所需时间和慢充功率。

若在停驻时间段内，慢充无法满足用户用电需求，则采用快充。具体判断式如下，若满足则采用慢充，不满足则采用快充：

(8)

电动汽车活动范围为城市内，距离均不远，且典型电动汽车续航能力均达300 km以上，因此不考虑中途充电行为。结束一天的行程返回家中后有足够的充电时间，因此默认归家后进行慢充直至满电结束。

2.6 考虑需求响应的充电需求补充模型

引入分时电价和奖惩机制，激励车主为达自身经济收益最大化，主动参与供需平衡调节[20]。首先确定EV是否有需求响应潜力[21]。若在停驻时间段内，EV参与需求响应不影响下一次行程进行，则判断该EV具有需求响应潜力。若EV参与需求响应后导致出发电量无法满足下次行程所需电量，则该EV不具有需求响应潜力。具体计算方法如下：

(9)

式中：DRP为第e辆EV的需求响应潜力指标；Pcharge为EV的充电功率。

采用需求价格弹性系数ε(h,k)来表征用户因分时电价而调节自身用电需求量的行为，引入需求响应的负荷模型如下：

(10)

式中：Q(h)、Q0(h)、ΔQ(h)分别为用户h时刻DR后的电力需求量、原电力需求量和电力需求改变量；P0(h)、ΔP(h)分别为h时刻原电价及执行DR后的电价改变量；C(h)为当系统供不应求时，用户h时刻削减单位负荷得到的补贴；D(h)为当系统供不应求时，用户h时刻未按照合约削减负荷，实行每单位负荷为D(h)的惩罚。

3 充电负荷计算

采用蒙特卡洛模拟1 d内EV的时空分布情况，以15 m为步长，蒙特卡洛仿真次数设为1 000，一次蒙特卡洛模拟流程如图2所示，具体步骤如下：

图2 一次蒙特卡洛电动汽车时空负荷预测流程Fig.2 Time-space load forecasting flow chart of Monte Carlo electric vehicle

1)基于路网模型、用户模型、需求响应模型获得单辆电动汽车每段行程的充电起止时间、充电地点时长等时空分布信息；

2)在一次蒙特卡洛模拟中，将每辆EV在各节点的充电负荷相叠加，获得区域内Nev辆EV在各交通节点的负荷分布情况，根据路-电节点耦合关系，归算至配电网。

不同典型日的EV充电行为有显著的差别，直接将典型日EV负荷叠加至可靠性评估中使用的基础年负荷数据中是不合理的。因此需将工作日、休息日1 d仿真所得的负荷转化为时变年负荷，便于4.2节进行可靠性评估使用。各节点的年负荷分布情况具体转化式如下：

(11)

4 含EV的配电网可靠性评估

4.1 可靠性评估相关指标体系

传统的可靠性评估主要从元件故障率、故障持续时间出发，分析整个系统的停电率、停电时长、用户供电可用率及负荷缺供量。但对EV接入的配电网可靠性进行评估，需要考虑系统故障时孤岛内DG出力波动及EV负荷波动对系统可靠性的影响，量化EV作为用户对配网可靠性的评估，传统方法缺少此方面内容，因此本文增加电动汽车充电稳定率指标用于评估含EV的配电网可靠性。

参考文献[10]，传统可靠性评估采用的指标有：系统平均停电频率指标(system average interruption frequency index，SAIFI)、系统平均停电持续时间指标(system average interruption duration index，SAIDI)、平均供电可用率指标(average service availability index，ASAI)、系统期望缺供电量指标(energy not supplied index，ENSI)。本文在此基础上，提出以下指标：

电动汽车充电稳定率指标CSR：

(12)

式中：Ma为a节点年均充电电动汽车数目；Fa为a节点年均受停电影响的电动汽车数目；b为节点总数。

4.2 基于双向层级结构的可靠性评估方法

传统可靠性评估算法计算效率低下，考虑开关故障的双向层级结构可靠性评估算法计算效率高，能够精确地对系统进行可靠性评估[22]。基于双向层级结构的可靠性评估如图3所示，其评估算法相关步骤说明如下：

图3 基于双向层级结构的可靠性评估流程图Fig.3 Flow chart of reliability evaluation based on bi-directional hierarchy

1)输入DG出力及电动汽车负荷样本；

2)以断路器及隔离开关为边界形成元件块，并计算元件块等效可靠性参数；

3)以主电源至主馈线末节点为正方向，上游元件故障会对下游元件块产生影响，开关故障融合至下游相邻元件块，顺向传递可靠性参数；

4)以隔离开关为首的元件块出现故障会对上游元件产生影响，开关故障融合至相邻逆向下游元件块，逆向传递修正元件块可靠性参数；

5)比较孤岛内DG出力与总负荷大小，确定孤岛成功形成的概率[23]；

6)采用启发式策略，优先削减离DG电气距离近的负荷，修正孤岛内负荷的可靠性指标；

7)计算系统可靠性指标。

5 算例仿真

5.1 仿真参数

本文首先按照某城市进行路网建模。算例城市路网如图4所示，该路网包含23个节点、35条道路。各道路长度数据见附表A1，红绿灯分布、自由流速度、道路通行能力、饱和度参考文献[18]。下文为简化描述，如无特殊说明，节点均指交通网节点。居民区(H)1为节点1—7，居民区2为节点16—23，工作区(W)为节点13—15，商业区(R)为节点8—12。路网拓扑图如图4所示，图4中道路长短不代表实际道路长短。配网测试系统以如图5所示的改进的IEEE-RBTS Bus6测试系统中主馈线F4为算例。元件可靠性参数、基础负荷数据参考文献[24]。各类开关的切换时间为1 h。在分支线53、59处加入2台风力发电机(wind turbine generator，WTG)，WTG相关参数见附表A2。为简化分析，本文假设各地点均有充裕的充电设施。依据临近性原则，充电桩节点优先接入与自身地理位置直线距离最近的电网节点。路网节点和配电网节点的对应关系见附表A3。

图4 算例城市路网图Fig.4 Example of urban road network

图5 IEEE RBTS Bus6 系统接线图Fig.5 Wiring diagram of IEEE RBTS Bus6 system

电动汽车相关参数见附表A4。不同类型日下各出行链占比如附表A5所示，峰谷时段划分采用文献[25]所提方法，各时段电价见附表A6。奖励与惩罚分别为0.20、0.30 元/(kW·h)，需求价格弹性系数矩阵为：

(13)

5.2 结果分析

算例区域典型工作日及休息日EV时空负荷在各节点各时段的分布如图6所示。由图6可知，不同典型日EV充电负荷在时间、空间上的分布情况各不相同。工作日充电负荷成双峰特性，主要集中分为两大部分。一部分分布于06：00—10：00，在交通节点13—15，这是因为工作日上班导致电量消耗，至工作地点充电产生。另一部分分布于16：00—21：00，在工作区外的节点，这是因为下班后至商场或归家充电所产生的。休息日充电负荷集中于居民区，时段08：00—16：00，这是因为休息日06：00—14：00出行至商场的EV归家后充电产生。这符合实际情况，也证明了本文方法的有效性。

图6 不同典型日充电负荷时空分布Fig.6 Spatial and temporal distribution of charging loads in different typical day

图7表征了不同典型日基础负荷、计及电动汽车负荷以及考虑需求响应这3种情况下算例区域一天内各时段的负荷分布。可以看出，工作日16：00—20：00，电动汽车负荷叠加基础负荷，极大提升晚高峰峰值。休息日09：00—14：00，二者叠加形成午高峰。但按照所提策略引入DR后，使得EV转移充电时间，各时段负荷波动过大得到改善，工作日负荷峰谷差由6.65 MW降低为4.59 MW，休息日负荷峰谷差由4.08 MW降低为2.83 MW，波动性明显减小，有削峰填谷的作用。

图7 不同典型日不同情况下区域总负荷曲线Fig.7 Regional total load curve under different typical days and conditions

应用本文提出的评估算法，构建5种场景进行可靠性评估，其可靠性指标如表2所示。场景1：含DG，无DR；场景2：含DG、EV，无DR；场景3：含DG、EV，考虑分时电价(即奖励与惩罚均为0元/(kW﹒h))；场景4：含EV、DG，同时考虑分时电价、奖惩制度(奖励为0.2元/(kW﹒h))；场景5：含EV、DG，同时考虑分时电价、奖惩制度(奖励为0.4元/(kW﹒h))。

表2 不同场景下的系统可靠性指标Table 2 Values of system reliability indices in different scenarios

由表2可以看出，对比场景1和场景2可知，EV的接入使得配网可靠性降低。这是由于车主自身用车，习惯于午间及晚间到达工作地点或归家后立即对EV进行充电，大规模EV接入所产生的无序充电负荷与基础负荷的早高峰、晚高峰叠加，进一步扩大负荷峰谷差，对配网可靠性产生不利影响。对比场景2和场景3可知，分时电价的实施，通过电价水平引导车主调整自身用电需求。从场景3、4、5可得综合电价机制与激励机制的需求响应可以更进一步引导电动汽车参与削峰填谷，改善配网可靠性。同时，随着奖励水平的提高，EV参与需求响应的积极性提高，配网可靠性进一步提升，但过高的奖励水平将加大电网支出，因此需控制奖惩水平，使二者均衡，以获得最大收益。

为更深入分析EV参与需求响应对配电网可靠性影响的作用机理，取节点8、9、10、11、12形成的孤岛1进行分析。图8为孤岛内风力机组出力及总负荷DR前后的分布情况，表3为孤岛内各节点DR前后的可靠性指标。由图8可知风电机组出力具有很强的不稳定性，不能时刻维持供应孤岛内总负荷的需求。由表3可知，考虑DR后，孤岛内各节点故障平均持续时间均缩短，这是因为EV参与DR后，10:00、11:00、16:00负荷相较于原负荷降低至风力机组出力以下，若此时系统发生故障，孤岛内负荷不会发生停电，因此其故障平均持续时间降低，可靠性提高。

表3 孤岛1各节点可靠性指标Table 3 Reliability index of each node in island 1

图8 孤岛1中各负荷及风电出力情况Fig.8 Load and wind power output in island 1

为验证路-电耦合特性对EV时空负荷预测及可靠性的影响，设定场景1为考虑路-电耦合，场景2为仅考虑电网，不考虑交通网耦合所产生道路拥挤、通行能力受限等情况的影响，车速全程设定为60 km/h。图9为各场景节点负荷分布情况，可以看出，路网的道路通行能力、红绿灯因素等交通信息会对EV时空负荷分布产生影响，虽在部分节点类似，但还是有所差异。同时也可看出节点15充电需求最低，节点5充电需求最高，可以此作为未来充电桩数量规划的依据。

图9 不同场景下各节点负荷分布 Fig.9 Load distribution of each node in different scenarios

选取节点9、11、22、23为例，比较两种场景下故障平均持续时间这一可靠性指标，其结果如表4所示。

表4 路-电耦合特性对可靠性的影响Table 4 Influence of road-electricity coupling characteristics on reliability

路-电耦合特性实质为考虑道路因素对车辆实际行驶路线及速度的影响，在道路拥堵时选取距离远耗时低的路线，更贴近实际。车辆实际行驶路线的变化会改变EV耗电量，继而改变EV充电负荷大小。因此路-电耦合特性影响的深浅可用充电负荷变化程度的大小来衡量。

由表4可得，考虑路-电耦合前后，节点9、11充电负荷变化微小，负荷增长幅度为1～2 kW，这是因为该节点位于路网中部，且与之连接的道路基本为普通路，因此各节点出发至此的耗时低及距离低的路径大致相同。节点22、23位于路网最右侧，左侧各点至节点22、23的路线组合有多种方式，耗时低及距离低的路径不同的概率大，因此节点22、23充电负荷相较于节点9、11增幅大，路-电耦合特性在节点22、23的作用更为明显。当系统发生故障时，考虑路-电耦合特性后，总负荷增长，DG出力无法满足孤岛内总负荷需求的概率增高，造成DG出力低于孤岛内总负荷大小时，孤岛内负荷被反复切除，因此节点9、11、22、23的故障平均持续时间均增大，可靠性降低。且由于路-电耦合特性在节点22的作用大于节点11，考虑路-电耦合特性前后，节点11、22的故障平均持续时间分别增加0.001 9 h/a、0.022 8 h/a，可见路-电耦合作用越大，可靠性降低幅度越大。综上，说明了考虑路-电耦合特性对含EV的配网可靠性评估的重要性。

6 结 论

1)本文所提充电负荷预测模型能够更准确地预测电动汽车充电负荷时空分布情况，可为未来充电桩建设规划等提供依据。

2)无论工作日还是休息日，电动汽车无序充电都造成“峰峰叠加”，不利于配电网稳定运行。

3)所提电动汽车需求响应补充模型可有效改善配电网可靠性指标，为电力系统运行与调度提供重要依据。

4)在对电动汽车时空负荷进行预测及其对配网可靠性影响进行评估时需考虑路-电耦合的影响。

本文主要以电动私家车为研究对象，未考虑电动公交车、出租车等其他类型电动车，下一步可拓展对全种类电动汽车负荷进行建模分析。本文在交通仿真及参数设定方面做了一些假设，如假设各地点均有充裕的充电设施，车主沿耗时最短路径行驶，归家后直接充电，未考虑多日一充。随着电力、交通、通信网络之间的联系更加紧密，车主的出行规律将更为复杂，下一步可开展更为精细化的电动汽车时空分布负荷预测及可靠性评估。