基于LSTM神经网络的电动汽车充电站需求响应特性封装及配电网优化运行
2021-06-09薛溟枫毛晓波潘湧涛杨艳红赵振兴李彦君
薛溟枫, 毛晓波,潘湧涛,杨艳红,赵振兴,李彦君
(1.国网江苏省电力有限公司无锡供电分公司, 江苏省无锡市 214000;2.中国科学院电工研究所,北京市 100190)
0 引 言
随着电动汽车的快速增长,大规模电动汽车充电具有随机性、时空耦合性的特点,对配电网运行造成巨大挑战。通过基于价格的需求响应,引导电动汽车在大时空范围有序合理地充电成为重要的技术手段[1-2]。
当前针对电动汽车充电价格及电动汽车充电行为的研究大多以电网运行效益为目标,通过分时电价机制引导电动汽车有序充电。例如,文献[3]引入价格弹性系数并考虑电动汽车出行不确定性和对电价响应的不确定性,以电动汽车代理商的收益最大制定分时电价策略。文献[4]在考虑电动汽车用户等待时间的基础上,以充电站利润最大为目标对电价进行动态调整,以提高电价制定者的收益。这类定价策略并未考虑交通网络拓扑结构、拥堵状况以及实时充电价格之间的交互影响,不能精确模拟电动汽车充电站需求响应特性。
同时,电动汽车充电站参与配电网需求响应,需要向上级电网调度机构提供其详细物理模型,并且上级调度机构需要基于详细物理模型建立全局优化调度模型并进行求解[5]。配电网调度机构面临众多充电站繁重的详细模型管理和维护工作,在实际中往往发生模型信息缺失或错误的情况。另外在未来市场化环境下,由于市场竞争需要,各充电站将不愿公开其内部模型信息,上级调度机构仅可获得其报价数据,从而不能实现基于物理模型的优化调度计算。因此,基于数据驱动的调度特性封装模型作为解决方案得到越来越多关注。文献[6]研究了基于数据驱动方式的电动汽车需求模型,并进行了仿真验证。文献[7]提出一种以长短时记忆神经网络作为共享层的多任务学习综合能源负荷预测方法,经由共享层模拟多元负荷间的耦合特性,进而达到提升预测精度的目的。文献[8]提出了一种由长短期记忆(long short-term memory,LSTM)自动编码器构成的负荷聚类方法。利用LSTM的时序记忆能力和自动编码器的非线性特征提取能力,实现了考虑负荷时序特性的自动特征提取和非线性降维。
在电动汽车充电站参与配电网优化运行方面,文献[9]研究了电动汽车充电站消纳白天光伏出力高峰时期的电力,平抑分布式光伏的出力波动,促进清洁能源消纳;文献[10]构建了储能电站、数据中心和电动汽车充电站的数学模型,采用粒子群优化算法确定储能站的最佳运行策略;文献[11]以可再生能源利用率最大、电网负荷波动最小和峰谷差最小为目标,采用了多种群和动态自适应策略,对换电站中的充电功率进行优化,未考虑电动汽车弹性和需求响应。文献[12]考虑电动汽车和可控负荷的特性, 采用机会约束对不确定性进行处理,建立了需求侧负荷响应的数学模型以及交易的最优竞价模型。由于电动汽车需求响应与光-储-充电站运行策略存在直接的耦合关系,并且与电价机制密切相关,上述文献中并未将分时电价机制与光-储-充电站运行控制综合进行研究。
本文提出基于数据驱动和LSTM深度神经网络的电动汽车充电站需求响应特性模型和分析方法。首先提出单体电动汽车充电模型和计及交通网络拓扑结构的电动汽车行驶特性,建立区域电动汽车充电站负荷需求响应计算方法,用来生成神经网络训练模型的原始数据;在此基础上,提出基于LSTM深度神经网络的电动汽车充电站需求响应模型封装方法,得到电动汽车充电站充电成本和充电功率响应之间的映射模型;进一步,构建考虑电动汽车充电站需求响应的区域配电网运行电压优化模型,并提出基于粒子群优化(particle swarm optimization,PSO)算法的模型求解方法;最后通过对包含3个充电站的IEEE-33 节点系统的算例分析,验证基于数据驱动的需求响应封装模型对配网电压越限风险优化方法的有效性。
1 电动汽车充电行为分析与需求响应
传统的电动汽车需求响应需要通过交互迭代完成,运营商很难获取准确的电动汽车充电行为特性。本文首先分析随时间变化的电价、路网中充电站位置以及电动汽车行驶阻塞因子与充电负载关系的相关模型;然后将时变的电价、阻塞因子纳入特征决策变量,采用LSTM深度神经网络对电动汽车的充电行为需求响应模型进行封装训练,实现通过电价、路网状态阻塞因子对充电站有功负载的准确预测;进而区域配网根据训练好的需求响应模型结合自身目标函数对各充电站的实时价格进行优化调节,引导电动汽车参与需求应用与合理地选择充电站,从而降低大规模电动汽车充电造成的配电网电压越限等风险。总体研究思路框架如图1所示。

图1 充电行为封装与配电网优化研究框架Fig.1 Research framework of charging behavior encapsulation and distribution network optimization
数据集是基于数据驱动的电动汽车需求响应模型封装和优化运行的基础。数据集可以通过电动汽车和充电站历史交互信息获取,但是历史数据并不能覆盖所有场景,因此,需要通过电动汽车和充电站的物理模型增补数据,进行数据增强。下文将介绍通过仿真获取电动汽车数据的方法。
1.1 单体电动汽车充电模型
根据出行特点可以将电动汽车分为运营型车辆、家用电动汽车、电动公交车等。运营型车辆,每日出行次数多,行驶时间长,对充电时长以及充电价格比较敏感[13]。家用电动汽车通常往返于居住区和工作区,停车时间较长,有足够的充电时间,但使用的随机性较大。电动公交车有固定的行驶路线,且通常有专门的充/换电站,其充电行为较为固定。对于商业运营充电站,其主要客户为营运性电动汽车、部分私家车以及少量外地临时充电汽车,故本文的主要研究对象是可以应用价格进行需求响应引导的运营型车辆和家用电动汽车。
通过对电动汽车的深入调研,考虑电动汽车的行驶参数包括电动汽车行驶位置、出行时间、电动汽车当前电量、电池容量、续航里程、单位里程耗电量等[14-15]。电动汽车的充电行为受多种因素的影响,如电动汽车剩余电量(state of charge,SOC)、充电电价/服务费、到充电站的距离、去充电站所用时间等。假设电动汽车在道路上行驶,当剩余电量低于阈值或者不足以到达目的地时,会产生充电需求,车主通常会根据上述因素进行综合决策,选择合适的充电站进行充电。
电动汽车的耗电量随着行驶里程线性增加,t时刻剩余电量EEV,t可由式(1)计算:
EEV,t=η(EEV,t-1-d·ΔWEV)
(1)
式中:EEV,t-1为t-1时刻的剩余电量;d为电动汽车行驶里程;ΔWEV为该车型单位里程耗电量;η为电动车效率系数,考虑电动汽车在实际行驶过程中的加速和减速过程,在0.9~1.0范围取值[16]。
假设不同电动汽车电池容量EEV服从式(2)的Gamma分布[16]:
(2)
式中:f(·)为电动汽车电池容量分布函数;α为形状参数;β为逆尺度参数;Γ(α)为伽马函数,根据不同车型的电池不同,其参数值参考文献[16]。
基于上述单体电动汽车参数特征的概率密度,采用蒙特卡罗(Monte-Carlo)方法进行抽样,以仿真大规模电动汽车行为特性。蒙特卡罗方法是一种以概率统计理论为指导的,以随机模拟和统计为手段的数值计算方法[17],该方法从随机变量的概率分布中,通过随机选择数值的方法产生符合该随机变量概率分布特性的随机数值序列,并将其作为输入变量进行特定的模拟试验。
通过蒙特卡罗抽样得到的电动汽车单体的行驶参数,其充电行为决策包含多个目标,分别为:到充电站的距离、充电费用和充电所需时间。本文以电动汽车选取充电成本最低的充电站为假设前提,将多目标综合决策转化为单目标形式,计算公式为:
(3)

1)到充电站的距离。
本文采用Floyd算法计算待充电点到充电站的最短路径[18],计算公式为:
(4)
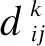
2)充电费用。
(5)

电动汽车总的充电电量Wch为电池容量Ecap与电动汽车剩余电量EEV,t之差,计算公式如下:
(6)
式中:ρ为电动汽车电池的充电效率系数。
3)总充电时间。
电动汽车用户对充电时间敏感度较高,总充电时间计算公式如下:
(7)

(8)
Tch.t=Wch/Pc
(9)

1.2 考虑路网状态的充电站负荷模型
为了仿真交通网络拓扑结构、拥堵状况以及实时充电价格之间的交互影响,本文使用基于电动汽车出行概率(origin destination,OD)矩阵,并考虑地理信息数据建立包含网络拓扑、车速-流量关系的城市交通模型[19]。根据统计概率抽样生成电动汽车仿真的初始时刻和初始SOC,根据OD矩阵,抽样出单体电动汽车的出行起点与行程终点。采用Floyd算法计算出从起点O到终点D的最短路径,并根据城市交通模型计算得到每条路段的车速,对电动汽车在城市路网中行驶行为进行仿真。
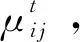
(10)
式中:vij,0为i-j路段的零流速度。
进一步,根据电动汽车电量水平确定待充电时刻和待充电位置,得到电动汽车充电负荷的时空仿真数据。根据充电站选择模型,模拟电动汽车选择综合成本最低的充电站进行充电,从而统计出各充电站每一时刻的充电功率。
本文的道路交通网络采用文献[19]中的29节点网络,如图2所示,包含29个路网节点及49条道路。其中节点17—20为办公区,节点21—29为商业区,其余为居民区。在节点6、21、28设有充电站。

图2 包含不同功能区域划分的道路交通网络Fig.2 Road network accross different functional areas
典型工作日中07:30—08:30和17:30—19:00期间为早晚出行高峰,居民区和办公区间的路段道路饱和度相对较高,该路段上的行驶速度较小,因此拥堵因子也较大;非高峰时段拥堵因子逐渐递减。周末及节假日中商业区周边的道路拥堵系数相对较高。
1.3 价格对充电行为的影响
电动汽车用户参与分时电价调节的响应度受价格变化的影响。充电站根据负载率的大小对电价(λ)进行调整,来达到引导电动汽车有序充电的目的。电价与充电站负载率关系如图3所示,在区域①,随着充电站负载率rcs的增加,充电价格线性增加;在区域②,充电站满负荷运行的情况下,入站充电的电动汽车排队充电,充电价格达到最大值。

图3 价格与充电站负载率关系曲线Fig.3 Relationship between price and charging load rate
将充电价格λ定义为一个分段函数:
(11)
式中:λLL、λUL分别为电价下限和电价上限;系数k=Prt/Pmax,为充电站实时功率Prt与最大功率Pmax之比;rcs为充电站负载率;rcs,m为充电站负载率临界值。
图4为某天充电站充电功率和充电价格曲线,每15 min一个点,可以看出,电动汽车充电需求在时间上的分布不平衡,11:30—13:00为一个高峰,16:30—17:30为一个小高峰。
结合图5充电价格曲线可以看出,随着充电需求的增加,充电价格相应调整,其峰值时间与图4中充电需求峰值时间一致。可以通过相对较高的充电价格,引导部分车主选择负载率低的充电站充电,或者选择充电负荷低的时间段进行充电。
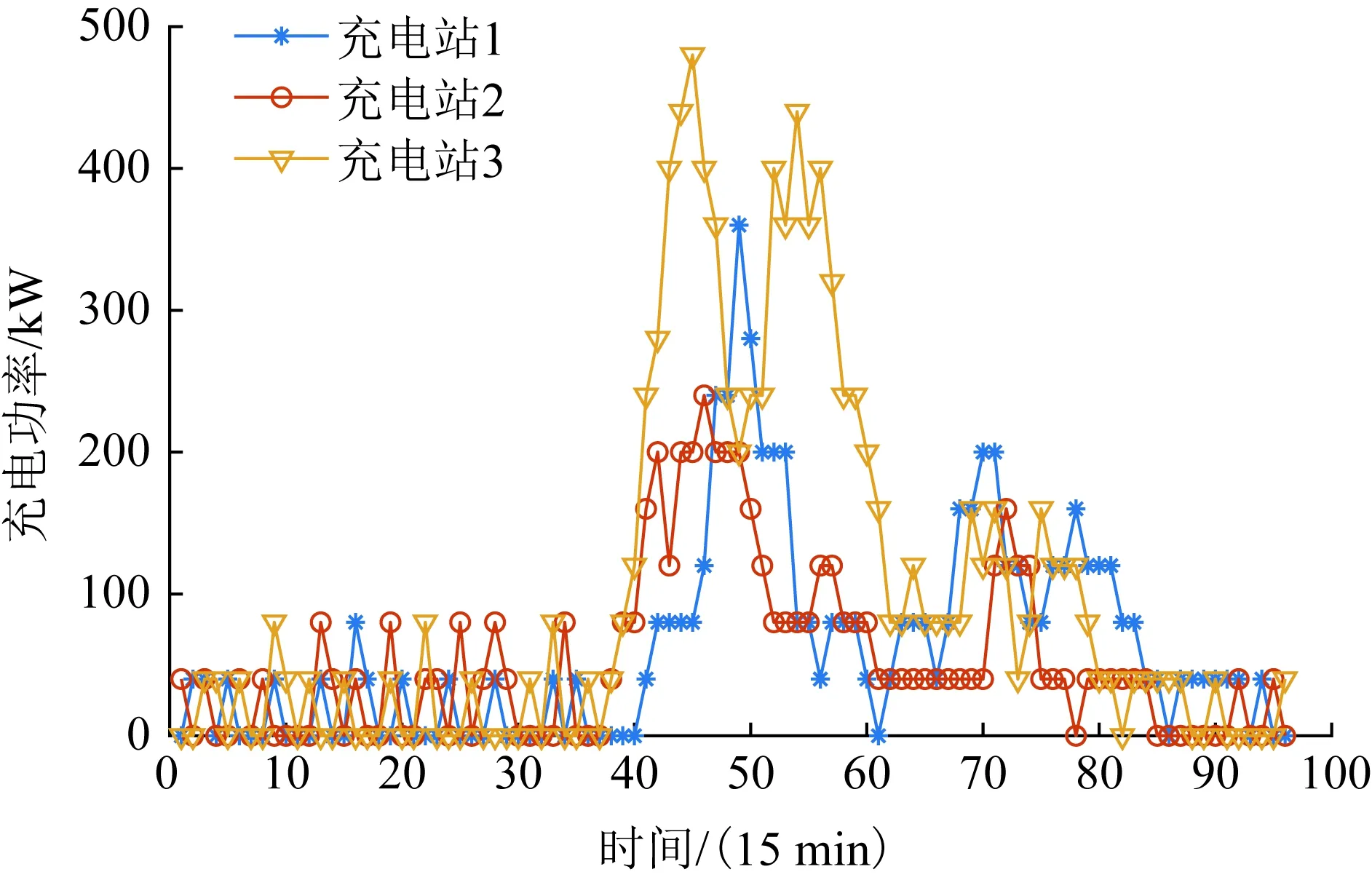
图4 充电站负荷曲线Fig.4 Load curve of charging station

图5 电动汽车充电价格曲线Fig.5 EV Charging price
根据电动汽车充电站安装的充电桩数量和模拟得到的电动汽车充电功率,可以计算t时刻第k个充电站的充电功率:
(12)

2 神经网络模型训练与封装
由于电动汽车充电站的负荷功率受汽车出行习惯影响,具有随机性、周期性的特点,因此充电数据具有时间序列的特征。目前由于循环神经网络(recurrent neural network,RNN)存在序列过长时出现拟合精度下降的特点,而长短期记忆模型(LSTM)通过增加了输入门、输出门、忘记门三个逻辑控制单元,在信息进入该模型时,LSTM中的三个逻辑门会对该信息进行选择性的记忆或遗忘,结合时序反向传播(back propagation through time,BPTT) 算法,克服了RNN容易产生梯度消失和爆炸的缺点,提升了拟合精度[20]。考虑对电动汽车充电站的汽车充电负荷功率进行实时一天96个等间隔时间点的多维时序数据采样。针对这样的长序列样本,LSTM网络比传统的RNN网络可以更好地解决预测精度问题。
本文通过对不同时段的3个电动汽车充电站的阻塞因子以及实时价格采用随机抽样的方式生成大量时序数据,并结合各充电站需求响应目标生成有功负载曲线,形成了输入特征为充电价格、路网阻塞因子,输出特征为各充电站充电功率的需求响应模型封装数据集。
样本的输入特征集:
(13)

样本的输出特征集:
(14)

封装训练模型结构如图6所示。由图6可知,需求响应有功负载的预测除了依赖于阻塞因子、实时价格信息外,还依赖于这些特征在时间维度的发展趋势。
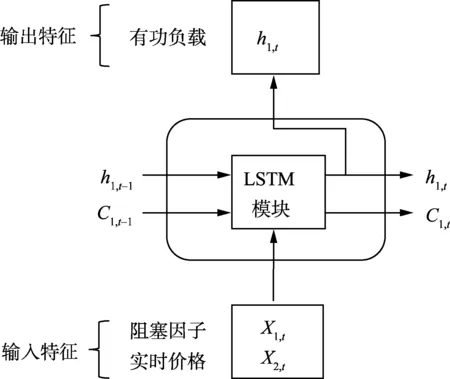
图6 LSTM封装训练模型Fig.6 Training model of LSTM package
3 配电网优化运行
由于充电站属于超大功率用电,因此充电站负荷分布直接影响到区域电网电压的安全稳定。本文考虑电网公司拥有或者运营的电动汽车充电站,其作为电动汽车充电站价格发布者有能力通过对充电站充电价格的制定来改变充电客户对充电站的选择,从而改变不同充电站的有功负载,达到对区域配网电压越限风险优化的目的。
3.1 目标函数
本文区域电网优化电价的目的旨在降低配网系统电压越限风险,因此区域配网的目标函数为:
(15)
(16)
式中:Ft为t时段节点电压的评价函数值;Vl,t表示配网系统中第l个节点t时段电压幅值的标幺值;λl表示惩罚因子,其中常数a< 评价函数中节点电压值由电力系统潮流计算节点功率方程确定: (17) 式中:PGl、QGl分别为节点l的电源发出的有功功率和无功功率;PLl、QLl分别为节点l负荷的有功功率和无功功率;Pl、Ql分别为节点l的总注入有功功率和无功功率;Vl为节点l的电压幅值;δlk为节点l与节点k之间的电压相角差;Glk、Blk分别为导纳矩阵的实部和虚部。 由式(17)可知,配网系统节点电压受节点功率分布的影响,即与充电站需求响应负载有关;又由式(11)可知,各充电站受区域配网实时价格引导,因此实时价格最终决定了配网电压越限运行的风险,即决定了式(15)节点电压的评价函数值。 考虑到电动汽车充电站与配网相连,优化配网系统需满足拓扑结构运行条件以及受到潮流功率平衡约束、电压幅值约束: (18) Vm.min≤Vm,t≤Vm.max (19) 式中:Pl,t、Ql,t分别表示t时段配网系统第l个节点有功、无功注入值;Pload.x,t和Qload.x,t分别为t时段第x个负荷节点有功、无功值;Ploss.y,t、Qloss.y,t分别为第y条线路t时段有功、无功的损耗;X、Y、L分别为负荷节点总数、线路总数和注入节点总数;Vm,t为配网系统第m个电压节点t时段电压幅值标幺值;Vm.min、Vm.max分别为第m节点电压幅值的最小、最大标幺值。 在上述考虑电动汽车充电站需求响应的区域配电网优化模型中,需要反复进行潮流计算,搜索最优电价,进而优化配网节点电压。在此采用粒子群算法,它可以解决黑盒优化问题,收敛速度快,调节的参数较少,全局搜索的鲁棒性强,对优化变量没有连续性、可导性的要求。通过对电动汽车充电站需求响应进行LSTM模型封装,结合粒子群算法,充电站的价格优化步骤如下: 1)在充电价格区间里随机初始化充电价格,结合阻塞因子值通过LSTM需求响应封装模型对各充电站有功负载进行预测。 2)将各个充电站有功负载带入配网系统对应负载节点,通过潮流计算后,计算区域配网目标函数式(15),记录并更新最优目标函数值和对应的最优价格。 3)判断PSO寻优迭代次数是否为最大迭代次数,如果是,则停止寻优,输出目前已求解出的最优目标函数值对应的最优价格;如果不是,则根据充电价格区间更新初始实时价格。 4)根据本轮更新的初始实时价格通过LSTM封装模型对各充电站有功负载进行预测。 5)返回第2)步,再逐序进行。 PSO优化充电站价格具体流程见图7。 图7 PSO优化充电站价格流程Fig.7 Flow of charging station price optimization based on PSO 为验证本文通过价格引导电动汽车充电站功率负载波动调节配电网电压思路的有效性,进行配网33节点系统的仿真分析,配网中考虑接入3组光伏电源,其配网拓扑结构如图8所示。 图8 配网33节点系统Fig.8 33-node system of distribution network 配网结构中,节点22为平衡节点,其与大电网相连,节点3、16、29分别接入3个电动汽车充电站,节点8、12、33分别接入3组光伏电源,3组光伏电源一天中有功出力波动状况如图9所示。 图9 3组光伏电源有功出力曲线Fig.9 Active power output curve of three groups photovoltaic power supply 本文通过Tensorflow1.0框架下LSTM模块对生成的28 800个时序样本进行封装训练。为提升训练精度,本文对序列样本采用归一化处理,将样本集的输入、输出时序数据全部转化为1以内的数据集。由于各个电动汽车充电站在配电网中的位置不同,需要将各电动汽车充电站数据分别进行训练,每个充电站的数据分别进行10 000次的训练。充电站LSTM封装模型训练误差见图10,样本训练集拟合效果误差精度RMSE(root mean squared error)分别为0.037 4、0.046 3、0.042 9,测试集样本误差精度RMSE分别为0.075 7、0.078 4、0.074 1。由于样本一天中有96个时间样本序列,为加速训练收敛速度采用了批量训练,批量大小选取30,学习率选取0.005,cell层隐含神经元数选取8,激活函数选取sigmod函数。 图10 充电站LSTM封装模型训练误差Fig.10 Training error of charging station LSTM package model 充电站的充电功率受实时充电价格所影响,并且已将各充电站实时充电价格、阻塞因子与各充电站的充电功率的隐性函数关系进行了封装和训练,因此配网可以利用已经训练好的模型,通过改变各充电站实时充电价格对配网电压越限风险进行优化。 本文封装模型的输入特征为阻塞因子以及实时价格,特定时段优化时阻塞因子为固定因素。由于电动汽车充电站负载与实时价格具有相关性,区域配网只需通过PSO算法对电动汽车充电站价格进行引导,从而优化配网电压越限风险。价格优化时选取与样本相同的价格区间作为价格优化区间,具体优化步骤见3.3节。 图11为区域配网利用PSO算法优化节点电压的电压评价函数值迭代优化曲线,200次迭代优化后,评价函数值收敛于48.06。图12为某一时间断面上区域配网节点电压优化前、后的各节点电压标幺值情况,可以看出优化前多处节点电压越限严重,优化后各节点保持在电压上下限区间内,电压越限状况明显改善。 图11 节点电压评价函数优化曲线Fig.11 Optimization curve of node voltage evaluation function 图12 配网节点电压优化Fig.12 Node voltage optimization of distribution network 为进一步验证本文提出的价格引导充电行为优化配网电压的方法在时间维度上的可持续性,避免单一时间断面优化有效的偶然性,对其进行了连续时间的优化。图13展示了配网中4个节点(节点1、6、19、29)的电压在连续时间维度的变化情况,从图中可以看出,相比初始电压(蓝色),优化后的节点电压(红色)在连续时间断面都明显优于优化之前,配网电压的越限风险也显著改善。 图14为图13对应时间断面的价格优化策略曲线,展示了在与样本相同的价格区间里3个不同电动汽车充电站的价格策略变化情况。从图14中可以看出,不同时间充电站的价格波动区间不同,各个站的价格策略也相差较大。 图14 充电站连续优化价格策略Fig.14 Continuous optimization of price strategy for charging stations 本文对基于价格的电动汽车需求响应特性和封装调度模型进行了研究,在分析电动汽车行驶特性的基础上,提出了基于LSTM深度神经网络的电动汽车充电站需求响应模型封装方法,以电价为优化变量,引导电动汽车合理选择充电站,构建了减小配电网电压越限风险的优化模型。通过算例对比分析表明,在未优化前,电动汽车无序充电,造成多处节点电压越限严重;而通过价格优化后,各节点保持在电压上下限区间内,电压越限状况明显改善。3.2 约束条件
3.3 求解方法与流程

4 算例分析


4.1 LSTM封装训练效果

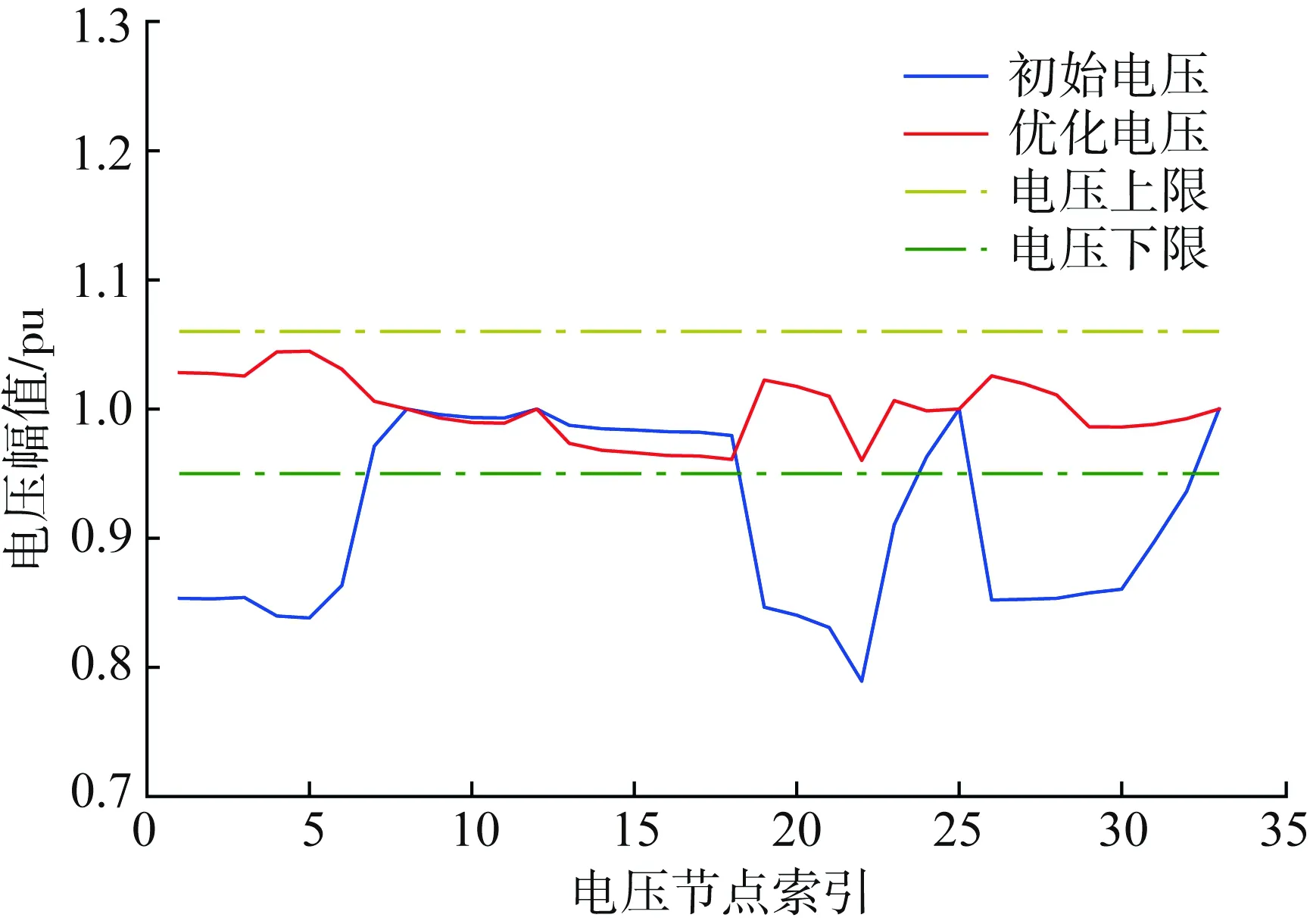
4.2 配网电压越限风险的优化分析


5 结 论
