考虑分布式可再生能源的通证激励机制设计与分散式电力市场研究

白昱阳，张俊，王晓辉，陈思远，高天露，刘鹏

(1.武汉大学电气与自动化学院，武汉市 430072；2. 中国电力科学研究院有限公司，北京市 100192)

0 引 言

随着全球化石能源的紧缺和环境污染加剧，加强环境保护、转变电能生产方式、开发可持续的清洁电能成为了世界各国的共识。以风能、太阳能等为主的可再生能源由于其储量大、无污染的特性，对于缓解能源紧缺、优化能源结构有着十分重要的作用[1]。

近些年，世界各国纷纷加大了对可再生能源发电的发展力度[2]，风能、太阳能等可再生能源的发电技术日益成熟，各国的风电或光伏发电的装机容量逐年提升。然而，由于可再生能源发电的随机性和波动性，可再生能源的并网率始终处于较低水平，大规模的弃风弃光现象亟需利用有效的技术手段解决。现阶段，单独依靠源侧的灵活性机组很难实现可再生能源的高比例消纳，还需要利用市场的手段，结合需求侧进行资源的联合优化配置，促进可再生能源在电力市场中进行消纳[3-6]。

分布式可再生能源作为可灵活配置的资源，在参与电力市场时会以大规模分散式主体的形式存在，这给集中式的电力市场出清带来了极大的挑战。因此，考虑到分散式市场主体的交易规模和隐私保护等因素，研究适合于包含大规模分散式主体的分散式电力市场模式具有重大意义。文献[7]分析了英国电力零售市场的改革与挑战，其通过分散式电力零售市场交易机制与监督体系促进电力零售市场的自由化。文献[8]对北欧电力市场进行了研究与分析，其利用分散式电力市场机制形成了首个跨国分散式电力交易市场，在可再生能源消纳、智能电网建设等方面取得了较好效果。

然而，可再生能源发电具有极大的随机性和波动性，会导致其参与到电力市场时无法与传统火力发电进行竞争。因此，需要设计合适的市场机制来促进可再生能源参与电力市场。文献[9]通过对国外电力市场配额制的研究，提出需要针对可再生能源配额制构建适合中国电力市场的市场交易体系，将用户纳入到可再生能源配额中，激发用户侧的灵活性资源帮助实现可再生能源的发展。文献[10]对国外的可再生能源配额制的研究情况进行了综述，分析了可再生能源配额制的实施框架及配额制对市场行为的影响，表明配额制可以促进可再生能源的消纳。文献[11]研究可再生能源发电参与电力市场时考虑了碳排放权交易的火电发电商、可再生能源发电商及政府的行为，说明了固定电价和绿色证书交易政策可以提高可再生能源发电的比例。文献[12]提出了结合可再生能源固定电价制和绿色证书配额制的发电商决策分析模型，此模型以市场所有发电商的总体利益最大化为目标，并采用多智能体粒子群算法进行求解，验证了所提市场优化模型的有效性，能够有效地促进可再生能源的发展。

可再生能源配额制能够很好地促进可再生能源的发展，然而可再生能源配额制主要存在以下局限性：1)可再生能源的配额是未来能源结构的发展目标，现阶段缺乏有效的激励手段[13]； 2)可再生能源配额制是政府强制要求可再生能源占比的一种模式，缺乏完全市场化的激励机制，市场主体参与促进可再生能源发展的积极性并不能得到有效的保证；3)市场中存在的可再生能源主体主要以大规模分散式的形式存在，这给可再生能源配额制的管控带来了挑战。

在此基础上，本文提出一种基于通证激励机制的分散式电力市场，以完全去中心化的方式进行分散式电力市场出清，且利用市场化的手段对可再生能源参与市场进行激励。首先对通证激励机制和分散式电力市场基本结构进行概述；然后建立以市场发电成本和碳排放治理成本最小为目标、考虑可再生能源参与的分散式电力市场出清模型；接着设计可再生能源发电-通证兑换机制，并建立考虑电价不确定性的含可再生能源发电商行为决策模型；最后进行算例仿真，验证所提分散式电力市场出清模型和通证激励机制的有效性。

1 考虑通证交易的分散式电力市场架构设计

1.1 通证激励机制

考虑到可再生能源具有不可调度性，单一的可再生能源发电机组难以参与电力市场，在激励机制不足的情况下发电商不愿意承担偏差费用带来的利润风险。传统的激励机制均存在一定程度的激励不足问题，例如碳排放市场中的碳价对发电商的利润影响太小，利用可再生能源获得的利润可能无法覆盖其出力随机性带来的惩罚费用，这是因为碳价作为强化物不具备较大的强化作用。

相比于传统激励机制中的强化物，基于通证激励机制的通证作为强化物会具有很多独特的优势[14]，主要表现在以下2个方面：

1)通证一般不受激励的短暂性状态影响，其价值不会随着单一权益的价值波动而波动，可以持续具有较强的激励作用；

2)通证一般选用具有安全、高效、流通速度快的物品，可以促使市场中各种利益主体进行交易，避免了传统激励机制只对部分主体具有激励机制的局限性。

考虑到电力系统有着节能减排和维持系统稳定的目的与需求，在本文中主要考虑对发电商使用可再生能源的激励机制。市场运营中心通过计算发电商使用可再生能源发电而减少的碳排放量，按照一定的折算率建立可再生能源发电量与通证奖励量的奖励关系，在发电商获得通证后允许其使用通证在市场中兑换市场竞争权益(例如电量市场的优先出清电量、调频市场的调频准入量等)，由于所对应的权益是与市场相关的收益，在不给市场造成额外的财政补贴压力的情况下最大化发电商的可能利润。

1.2 市场架构

本文所提的分散式电力市场由电量市场和通证市场两大部分组成，其结构如图1所示。电量市场是以分散式方式进行出清，各发电商通过信息交互的方式进行迭代共识与信息更新，在不依赖于市场中心协调机构的前提下形成市场的出清方案。通证市场是以挂牌成交、点对点交易的方式运行，发电商在市场运营中心挂出愿意出售的通证数量，通证的价格是根据通证市场中挂牌交易的情况而决定的，交易双方通过双向报价和协商撮合的方式来形成通证的交易价格。

图1 分散式电力市场运行结构图Fig.1 Diagram of the operation structure of distributed power market

如1.1节中所述，通证可以用于电量市场兑换优先出清电量，使用可再生能源的发电商会被奖励一定数量的通证，通证市场设置在电量市场之后用于市场各主体间进行通证交易。因为通证的权益、价格与市场电价有着一定的关系，且随着市场中通证的数量而改变。在通证市场中，发电商会根据远期电量市场的价格和市场中通证的交易情况来选择通证出售策略，最后通过点对点交易的方式与市场中购买主体完成交易。

2 含可再生能源的分散式电力市场模型

电力市场出清是一个发电商与用户的双边决策问题，对电力市场的均衡有着重要的意义。在电力市场的出清计算时必须满足电力系统的约束条件，如功率平衡约束、机组自身的出力及爬坡约束等。由于市场的出清电价一般作为市场的结算电价，对于参与电力市场的发电商来说，准确掌握市场的出清电价，则可以按照市场出清电价选择合理的报价策略，帮助发电商实现自身收益的最大化。本节在分散式电力市场出清的基础上，引入了可再生能源参与电力市场的激励机制，利用纳什均衡模型对通证市场的实时和远期市场价格进行出清，最大化通证激励机制在分散式电力市场中的促进作用。

2.1 分散式电量市场出清模型

2.1.1出清模型构建

在分散式电力市场中，建立基于直流潮流最优的分布式安全约束经济调度模型，在考虑了电力系统网络潮流约束的同时，从系统的经济性、可靠性等功能性目标函数出发对各节点发电资源进行优化调度。同时，由于考虑可再生能源参与市场带来的影响，在出清模型中将系统的碳排放治理成本作为目标函数之一。因此，含可再生能源的分散式电力市场的出清模型详述如下。

1)火电机组发电成本。

火电机组的成本即为发电的燃料成本，一般考虑为发电功率的二次函数，发电成本函数为：

(1)

2)可再生能源机组运行成本。

可再生能源机组运行成本考虑为发电功率的一次函数，运行成本函数为：

(2)

在本节考虑的是可再生能源和火电按比例上网的策略，假定可再生能源和火电的占比分别为σi和1-σi，且0≤σi≤1。

则可再生能源机组和火电机组出力分别为：

(3)

(4)

(5)

式中：Pi为发电商i的出力值。则发电商成本函数为：

Ci=ai[(1-σi)Pi]2+bi(1-σi)Pi+

(6)

3)碳排放成本。

由于可再生能源发电具有无污染的特点，几乎不产生对环境有害的气体，因此系统中增加可再生能源发电可以减少电力系统的碳排放，降低环境治理成本。含有可再生能源发电和火力发电的发电商i由于碳排放产生的环境治理成本为：

(7)

式中：φres和φT分别为单位可再生能源机组和火电机组出力产生的碳排放量；k0是单位碳排放量的治理成本系数。

根据式(1)—(7)，系统的总成本为：

(8)

式中:Ωb为电网中所有节点的集合。

4)约束条件。

(1)功率平衡约束：

(9)

式中：PLi为电网节点i的负荷总量；θi和θj分别为电网节点i和节点j的电压相角；Bij为电网节点i和节点j之间线路的电纳值；Ωi为与节点i相连的电网节点的集合。

(2)线路功率约束：

(10)

(3)发电机组功率约束：

(11)

(12)

2.1.2出清模型求解

根据共识-新息(consensus innovations approach, CIA)算法[15]的迭代形式，将拉格朗日函数L对拉格朗日乘子λ和θ的一阶偏导作为算法的梯度寻优方向，利用电网节点之间的信息交互，对节点信息进行分布式更新，最终迭代收敛到一个全局的最优解[16]。

拉格朗日乘子λ作为电网潮流平衡约束的影子价格，为系统节点间进行交互的信息之一，根据其一阶偏导最优性可作为电网节点的出清电价，在不考虑阻塞成本时，不同节点间的λ值最终会收敛到一个值，即为系统统一出清电价。系统出清模型的一阶最优性条件推导见附录A，因此可以利用节点间的交互信息对λ和θ进行更新，电网节点i的λ值更新过程如式(13)所示：

(13)

式中：k为迭代次数；α、β为迭代更新参数。

拉格朗日乘子θ也为节点间交互的信息，其根据拉格朗日函数对λ的偏导进行更新电网节点i的θ值，迭代更新过程如式(14)所示：

(14)

式中：γ为迭代更新参数。

在拉格朗日乘子λ和θ更新之后，对本地发电功率进行更新，在分散式电力市场中，表现为电网节点的发电商不断依据周围电网节点发电商的报量信息，不断调整自身的功率报量的过程，电网节点i发电商的功率更新公式如式(15)所示：

Pi(k+1)=

(15)

(16)

(17)

式中：δ为迭代更新参数。

以上的共识-新息算法通过各节点之间的信息交互和共识以分布式的方式完成。系统中各节点会与邻域节点交换并共识节点的电价与相角等数据，并根据邻域节点的数据更新自身的功率值，最终形成全网统一出清边际电价。

2.2 通证市场出清模型

在本节中，将奖励通证和可再生能源发电对应起来，建立通证市场，将通证对应的价值在市场中进行流通。通证市场在电力市场出清后进行交易，并不考虑发电商使用通证兑换其他权益获得的远期不确定收益，仅考虑发电商在通证市场中售出所持有的通证获得的收益。当发电商采用可再生能源发电时，根据其可再生能源出力通过一定的兑换率获取通证，如式(18)所示：

(18)

式中：Qi表示发电商i兑换获得的通证数量；ρ表示可再生能源出力-通证兑换率。

基于古诺均衡模型[17]的基本假设，建立通证市场的通证价格模型。因此，通证的市场出清价格和通证数量可以描述为如下的逆价格需求函数关系：

(19)

由于通证具有可流通和可持有的双重属性，发电商在获得通证后可以自行决定是否立即进行交易或者将其保留下来以便在未来进行通证交易时可获得更大的收益。参照电力市场的市场分类，将通证市场分为现货通证市场和远期通证市场，因此需要分别对现货通证市场和远期通证市场建立相应的通证价格模型。

1)现货通证市场通证价格模型。

现货市场的均衡出清比较直观，通过现货市场中存在的通证交易总量，可以求出均衡情况下的通证价格，现货市场通证价格-数量关系如图2所示。

图2 现货市场通证价格-数量关系图Fig.2 Relationship between token price and quantity in the spot market

因此，现货市场基于古诺模型的通证价格模型的系数可以表示为：

(20)

(21)

2)远期通证市场通证价格模型。

在古诺模型的基本假设中，数量和价格成逆需求关系，对远期通证市场建立通证价格模型需要通过对远期的最大通证总数进行估计，即为系统接下来时刻所有市场参与者获得最大通证数量且均保留通证至远期交易的情况，本文考虑为系统此后的总负荷需求对应的通证数量。远期市场通证价格-数量关系如图3所示。

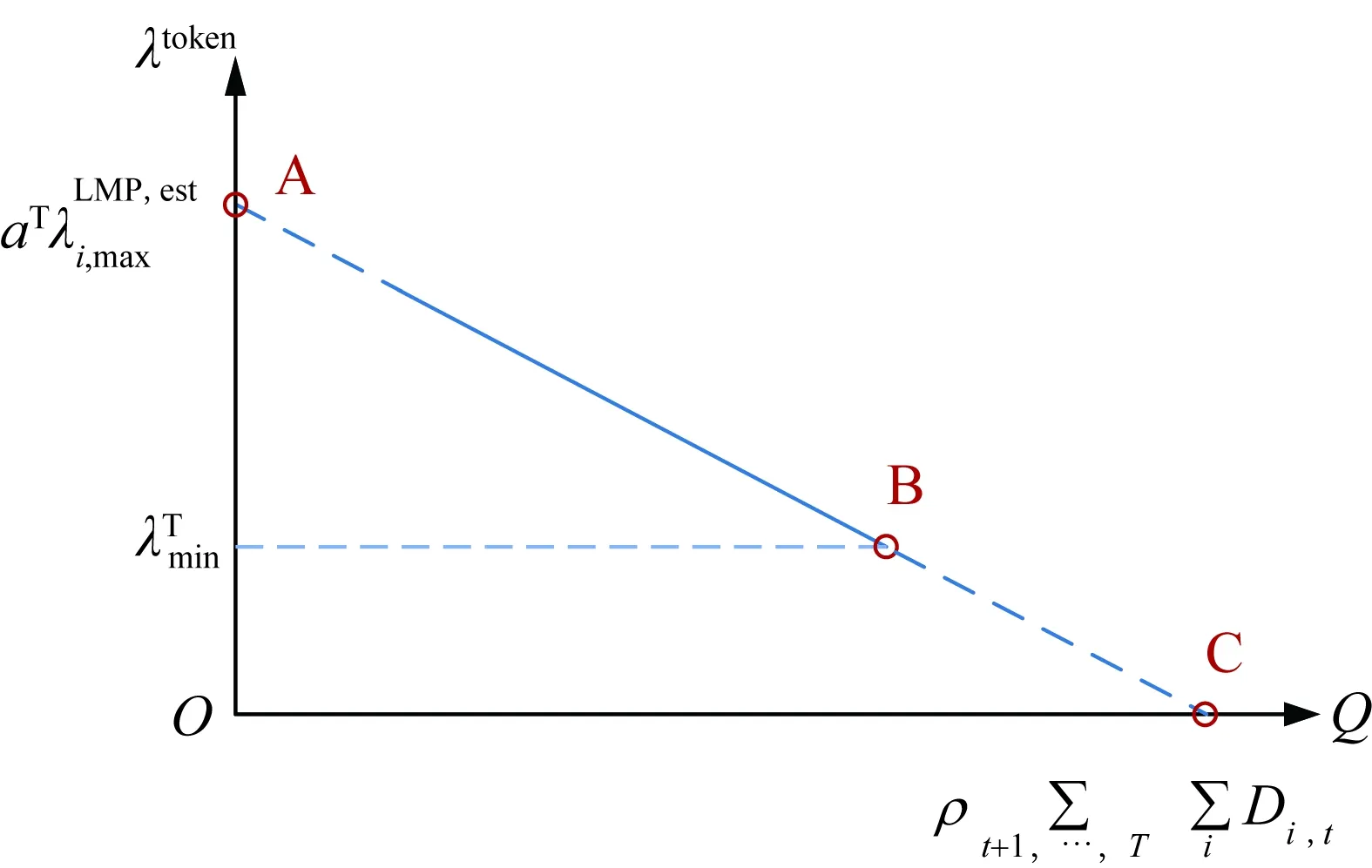
图3 远期市场通证价格-数量关系图Fig.3 Relationship between token price andquantity in the forward market

(22)

(23)

3 通证激励机制下含可再生能源的发电商决策模型

3.1 决策模型构建

考虑到通证的激励机制，发电商将会考虑在电力市场更多地采用可再生能源机组发电，以此兑换一定的通证从而在通证市场中获利。然而，由于可再生能源发电的随机性和波动性，较多地采用可再生能源发电可能带来较大的发电偏差惩罚费用，因此市场中的发电商会利用市场出清情况对自身发电策略进行最优决策。为了验证本文所设计的基于通证的激励机制的有效性，通过对发电商的行为决策建模来分析发电商在激励机制下的决策行为，以电力市场中的发电商为研究对象，建立发电商在电力市场和联合市场的联合决策模型。

(24)

3.2 不确定性建模

3.2.1可再生能源出力的不确定性处理

由于可再生能源的随机性和波动性，发电商的实际发电量可能和电量市场中出清电量存在偏差，导致市场偏差考核时为发电商带来惩罚费用，因此在发电商决策分析时需要考虑可再生能源发电的不确定性，本节对可再生能源的不确定性采用场景化的处理方式进行处理。

(25)

3.2.2基于IGDT的电价不确定性处理

对单一发电商进行行为决策分析时，由于各个发电商决策的出力波动以及市场用电的变化可能会导致日前市场统一出清电价(market clearing price, MCP)发生改变。针对单一发电商，考虑电价的不确定性因素，对电价的不确定性进行建模，以求得发电商在电价波动时的鲁棒收益，作为发电商决策的依据。

信息差距决策理论(information gap decision theory, IGDT)方法[18]可在概率密度函数缺失的情况下处理不确定参数，不失一般性，针对最小化问题，IGDT的模型可表达为如下形式：

(26)

式中：X为决策变量；ϑ为不确定参数；Hi(·)和Gi(·)为变量满足的不等式约束和等式约束函数；Φineq、Φeq分别为不等式约束和等式约束函数编号集合；Γ为ϑ的取值集合。且不确定参数ϑ的数学表达式可表述为：

(27)

(28)

式中：fb为目标函数基准值。IGDT的主要目的是帮助决策者适当调整决策变量，以避免由于不可控参数的不确定性使系统无法达到最低要求的风险。

本节将统一出清电价作为IGDT模型中的不确定参数，通过IGDT方法辅助发电商进行鲁棒性决策。并引入正参数ε，来描述决策者对于参数不确定性导致目标函数恶化的容忍程度。显然在ε给定的前提下，最优的鲁棒决策可以使系统容忍不确定参数最大程度波动，基于上述思想，式(28)可转化为式(29)：

(29)

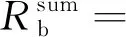
(30)

则本文在考虑电价不确定性时的发电商决策模型可描述为：

(31)

综上所述，基于本节的不确定性建模方式，式(24)构成了本节考虑可再生能源出力不确定性造成的偏差惩罚的发电商决策模型，式(24)—(25)、式(30)、(31)构成了考虑电价不确定性的发电商决策模型。

4 算例分析

4.1 算例描述

本节在修改后的IEEE-9节点算例上进行仿真验证，电网的拓扑如图4所示。其中在节点1和节点2上分别接入了风电机组和光伏机组，风电数据和光伏数据来源于某实际风电场和光伏电站的实际出力数据，风电和光伏的预测功率出力曲线如图5所示，电网中节点1、2、3、5和7为5个发电商的接入点，分别记作发电商1—发电商5。发电商2包括了常规火电机组和风电机组，发电商3包括了常规火电机组和光伏发电机组，发电商1、5和7为火电机组，系统中发电机发电数据如表1所示。本文将共识-新息算法中的参数设置为α=0.003/k0.98、β=0.001/k0.001、γ=0.000 5/k0.001和δ=0.005/k0.001，迭代次数设置为1 000次。市场中发电商的可再生能源某时刻预测出力值会影响该时刻自身的中标情况和市场的出清情况。

图4 某地区电网系统拓扑图Fig.4 Topology of a regional power grid system

图5 可再生能源机组功率预测值Fig.5 Power forecast value of renewable energy units

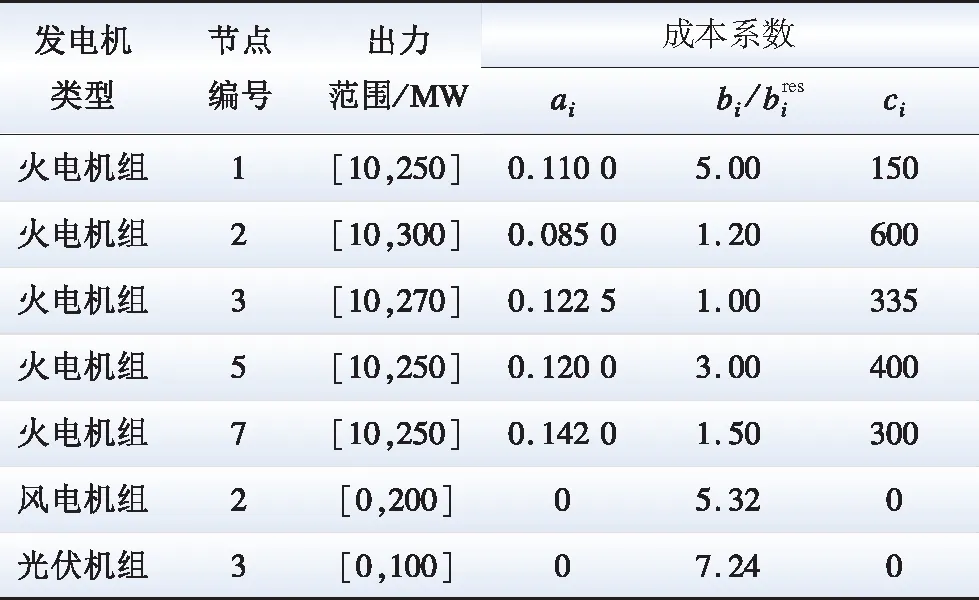
表1 系统中发电资源成本系数Table 1 Cost coefficient of power generation resources in the power system

4.2 分散式电力市场电价出清分析

4.2.1算法有效性分析

1)单时段市场出清求解。

假设市场中风电和光伏的上网比例均为0.4，为了更好地评估算法求解的有效性，选取风电和光伏均有较为可观出力值的12:00—13:00时段进行单时段市场出清求解。假设该时段的预测值精准，则风电的预测出力为70.40 MW，光伏的预测出力为61.75 MW。在系统节点5、7、9处有负荷需求，该时段的负荷需求分别为PL5=195 MW，PL7=100 MW，PL9=125 MW，市场出清的结果如图6所示。

图6 市场出清过程迭代过程图Fig.6 Iterative process diagram of market clearing

通过图6(a)可以看出，本文所提算法在600次左右开始趋于收敛，经过1 000次迭代求解，可以得出市场的出清电价为12.54美分/(kW·h)。从图6(b)中的曲线可以看出，考虑到风电和光伏的经济性和市场减少碳排放治理成本的目标，拥有风机的发电商2获得了较多的出清电量，而火电成本系数偏高的发电商3在配合光伏出力之后也获得了较为理想的出清电量，其余发电商利用火电出力配合系统进行功率平衡调节。5个发电商的出清电量分别79.34、105.24、65.74、86.79和82.89 MW·h。

仿真数据结果表明可再生能源的出力值对市场出清的影响较大，本节在后续仿真中需对可再生能源的上网比例和可用出力值进行影响分析。

2)全时段市场出清。

为了更好地分析可再生能源发电对市场出清的影响，后续对一天24个时段进行市场出清求解。考虑到不同节点的负荷差异性也会对市场出清情况有较大影响，仅假设节点7和节点9上均是固定负荷(即PL7=100 MW，PL9=125 MW)，仅在节点5上设置实时变化的负荷需求，其负荷需求曲线如图7所示。同样地，将风电和光伏的上网比例设置为0.4，市场出清得到的市场全时段MCP和系统中发电商的出力情况分别如图8所示，全时段MCP数据见附录B表B1。

图7 节点5的负荷需求曲线Fig.7 Load demand curve of node 5

通过对比图8中(a)和(b)的曲线可以发现，可再生能源参与电力市场可以极大地降低电价水平，而且可以减小电价曲线的波动区间，这是因为风机和光伏可以为系统充当备用电源，当系统负荷波动而火电机组容量不足时，充足的风机和光伏上网供电可以减缓市场的负荷需求冲击，从而避免出现电价剧烈升高的情况。另外，从图8(b)中可以看出，当风机可用出力大幅跌落时，电价也会出现小幅增长。在09:00—11:00时段和14:00—16:00时段，风机可用出力下跌导致电价激增，而在12:00—13:00时段光伏可用出力的上涨可以弥补风机可用出力的不足，会导致电价回落。在18:00之后，光伏可用出力为0，风机可用出力逐渐恢复，电价在小幅波动之后又会回落到相对较低的水平。另外，通过对比附录B表B1中各发电商的发电数据可以看出，含风机的发电商2和含光伏的发电商3总能获得较多的出清电量，这是因为含可再生能源的发电商具有较低的成本函数，能减少电力系统的总成本。

图8 全时段市场MCP曲线Fig.8 MCP curve of 24 hours

4.2.2可再生能源上网比例对市场出清影响

在上述某地区电网算例中，可以发现可再生能源出力对市场出清得到的MCP有较明显的影响，但存在可再生能源与火电打捆上网供电时会影响火电灵活性的问题。选取图5曲线中风电出力最大(在04:00时刻)和光伏出力最大(在13:00时刻)2个场景，调整可再生能源上网比例来分析其对市场统一出清电价的影响，结果如图9所示。

从图9中可以看出，在本节理想场景设置下可再生能源上网比例对市场MCP的影响较为直观，考虑到风电的经济性优于光伏，风机大规模接入后市场MCP将低于光伏大规模接入时的。因此，在后续的发电商决策分析中，发电商可再生能源与火电的上网比例会

图9 2种场景下可再生能源上网比例对市场MCP的影响Fig.9 Influence of renewable energy ratio on MCP under two scenarios

对市场实时出清时电价造成影响，在进行发电商利润分析时应考虑市场MCP的不确定性。

4.2.3算法鲁棒性评估

为了验证本文所采用的共识-新息算法的鲁棒性，将算法应用在IEEE-39节点标准算例中进行分布式市场出清，以验证其在较大的系统中的求解性能，将共识-新息算法中的参数设置为α=0.000 8/k0.98、β=0.000 1/k0.001、γ=0.000 035/k0.001和δ=0.000 1/k0.001。考虑到该方法通过节点之间的信息交互进行迭代与更新，对电力网络的拓扑变化具有自适应性，设置切机和切负荷2种场景来进行求解分析。在切机的场景中将节点30—33上的4个发电机组切除，而在切负荷的场景中将节点15、16、20上的负荷切除，市场的出清过程如图10所示。

从图10中可以看出，切机之后系统电源变少，在市场需求总量不变的情况下需求侧竞争较为激烈，导致市场统一出清电价数值变大；相反，切负荷之后系统需求量变少，在电源数量不变的情况下市场出清的统一出清电价数值变小。因此，共识-新息算法可以在系统运行状况和拓扑结构变化后，迅速收敛到新的市场统一出清电价，从而为分散式电力市场的实时出清提供可靠的保障。

图10 市场MCP迭代过程变化Fig.10 Iteration diagram of MCP

4.3 含可再生能源的发电商决策分析

4.3.1场景设置

本节在4.2.1节中实际电网系统的仿真结果基础上进行分析，出清结果选择可再生能源火电比例为0.4的情况，对系统中的发电商2进行分析，根据仿真结果可知系统24 h的统一出清电价与该发电商的全时段出清量，如附录表B1所示。仿真依据出力-通证兑换率ρ的不同分为3种情况，对于每种情况，又将其是否引入通证激励、是否考虑MCP不确定性可分为如下3个场景。

1)场景1：不引入通证激励，且不考虑MCP不确定性。该场景下发电商出力需满足日前市场出清的电量，可再生能源出力占比可自我调节，同时针对可再生能源出力的偏差值进行考核。

2)场景2：引入通证激励，但不考虑MCP不确定性。该场景通过引入现货和远期通证市场来激励发电商提高可再生能源机组出力。

3)场景3：引入通证激励，且考虑MCP不确定性。发电商需在场景2基础上进一步进行功率分配的鲁棒性决策，以最大程度抑制电价的不确定性。

仿真参数取值如表2所示。

表2 仿真参数取值Table 2 Simulation parameters

4.3.2仿真结果分析

仿真结果基于可再生能源出力-通证兑换率的不同分为如下3种情况。

1)可再生能源出力-通证兑换率ρ=0.05时。

在ρ=0.05时，基于上述数据与参数进行3个场景下的发电商可再生能源机组出力决策与通证市场行为模拟仿真，仿真结果如图11—13所示。其中图11为场景1、2下可再生能源与火电24 h出力情况对比；图12为场景2下现货/远期通证价格与发电商通证出售策略；图13为场景1、2、3下可再生能源出力对比。

图11 ρ=0.05，场景1、2下可再生能源与火电24 h出力情况Fig.11 Output diagram of renewable energy and thermal generation at 24 hours under Case 1 and Case 2 with ρ=0.05

图12 ρ=0.05，场景2下现货/远期通证价格与发电商出售策略Fig.12 Diagram of spot/forward prices and strategies of generators at 24 hours under Case 2 with ρ=0.05

图13 ρ=0.05，场景1、2、3下可再生能源出力对比Fig.13 Output diagram of renewable energy at 24 hours under Case 1, Case 2 and Case 3 with ρ=0.05

图11中的阴影区域是由于可再生能源机组的出力不确定性而对应的决策变量范围。从图11可以看出，2种场景下的可再生能源出力趋势总体上均与图5所示的风电机组功率预测曲线基本保持一致。相比场景1，场景2下发电商的可再生能源出力值得到了大幅提高，且随着可再生能源出力占比的提高，出力的不确定范围也逐渐增大，这也对火电机组的调节速度与精度提出了更高的要求。场景1下24 h可再生能源总出力1 124.356 MW·h，而在引入通证激励后，可再生能源总出力1 347.526 MW·h，出力综合提升19.856%，证明了通证激励在引导可再生能源出力方面的有效性。

从图12可以看出，在价格方面，通证现货市场波动较大，全时段内价格极差为3.3691 美元；而通证远期市场则较为稳定，在MCP较高时波动较小，价格极差为0.204 0美元。从通证出售决策方面可以看出，发电商在现货市场出售的通证数较为稳定，为远期市场保留的通证数波动更大。综合上述两方面信息，可以得出：相比远期市场，发电商对现货市场的通证价值估值更高，且当前时段的出力与价格变化对远期市场的通证价格影响较小，这也与实际市场的运行规律相契合；考虑到现货市场价格波动大风险高，相比于单次售出所有通证，发电商更倾向在现货市场售出固定数量的通证获得基础收益后，保留大部分的通证用于远期储蓄以实现总利润的最大化，通过计算可知现货市场售出通证的数量平均占发电商总通证数的29.154%。

由图13可知，对比场景2、3下的可再生能源出力曲线可以发现，在考虑电价的不确定性后，发电商选择进一步提高可再生能源机组的出力值以最大化对电价下跌的鲁棒性。这是因为相比火电机组可再生能源发电成本更低，故提升可再生能源出力占比能让发电商在更低的电价下保证期望的收益。综合3种场景下的可再生能源出力趋势与负荷曲线和电价曲线可以看出，在电价非高峰时段，可再生能源出力趋势基本与电价与负荷曲线一致；在电价高峰时期(11：00,14：00,16：00)，可再生能源出力值较低，这是因为虽然可再生能源机组发电成本更低，但考虑到其出力的不确定性而可能带来的偏差考核惩罚，发电商更倾向在电价峰值时段用传统机组出力以获得稳定的最大收益。根据仿真统计数据，场景3下可再生能源总出力为1 386.656 MW·h，相比场景2综合提升了2.904%。

2)可再生能源出力-通证兑换率ρ=0.10时。

当ρ=0.10时，3种场景的对比仿真结果分别如图14—16所示。

图14 ρ=0.10，场景1、2下可再生能源与火电24 h出力情况Fig.14 Output diagram of renewable energy and thermal generation at 24 hours under Case 1 and Case 2 with ρ=0.10

图15 ρ=0.10，场景2下现货/远期通证价格与发电商出售策略Fig.15 Diagram of spot/forward prices and strategies of generators at 24 hours under Case 2 with ρ=0.10

图16 ρ=0.10，场景1、2、 3下可再生能源出力对比图Fig.16 Output diagram of renewable energy at 24 hours under Case 1, Case 2 and Case 3 with ρ=0.10

从图14可以看出，当ρ=0.10时，场景1下24 h可再生能源总出力1 124.356 MW·h，而在引入通证激励后，可再生能源总出力1 547.383 MW·h，出力综合提升37.632%。具体分析和ρ=0.05情况类似。

从图15可以看出，在价格方面，通证现货市场波动较大，全时段内价格极差为3.336 4美元；而通证远期市场则较为稳定，在MCP较高时波动较小，价格极差为0.215 1美元。通过计算可知现货市场售出通证的数量平均占发电商总通证数的25.864%。具体分析和ρ=0.05时类似。

当ρ=0.10时，根据仿真统计数据，场景3下可再生能源总出力为1 578.421 MW·h，相比场景2综合提升了2.006%。具体分析和ρ=0.05时类似。

3)可再生能源出力-通证兑换率ρ=0.15时。

当ρ=0.15时，3种情况的对比仿真结果分别如图17—19所示。

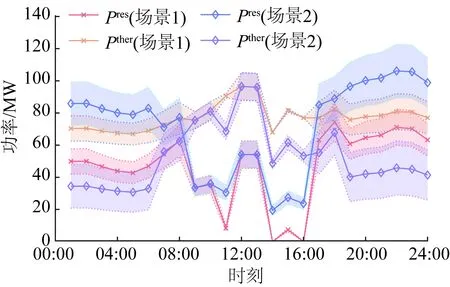
图17 ρ=0.15，场景1、2下可再生能源与火电24 h出力情况Fig.17 Output diagram of renewable energy and thermal generation at 24 hours under Case 1 and Case 2 with ρ=0.15

从图17可以看出，当ρ=0.15时，场景1下24 h可再生能源总出力1 124.356 MW·h，而在引入通证激励后，可再生能源总出力1 706.563 MW·h，出力综合提升51.790%。具体分析和ρ=0.05时类似。

从图18可以看出，在价格方面，通证现货市场波动较大，全时段内价格极差为3.304 1美元；而通证远期市场则较为稳定，在MCP较高时波动较小，价格极差为0.211 4美元。通过计算可知现货市场售出通证的数量平均占发电商总通证数的23.83%。具体分析和ρ=0.05时类似。

图18 ρ=0.15，场景2下现货/远期通证价格与发电商出售策略Fig.18 The diagram of spot/forward prices and strategies of generators at 24 hours under Case 2 with ρ=0.15

图19 ρ=0.15，场景1、2、3下可再生能源出力对比图Fig.19 Output diagram of renewable energy at 24 hours under Case 1, Case 2 and Case 3 with ρ=0.15

当ρ=0.15时，根据仿真统计数据，场景3下可再生能源总出力为1 736.616 MW·h，相比场景2综合提升了1.761%。具体分析和ρ=0.05时类似。

根据可再生能源-通证兑换率ρ的不同，对3种情况下发电商的决策行为分析详述如下。

从图11、14、17可以看出，在不同的可再生能源出力-通证兑换率下，相比不考虑通证激励的情况，发电商均产生更多的可再生能源出力，说明本文所采用的基于通证的可再生能源发电参与电力市场的激励机制是有效的，能够激励发电商采用更多的可再生能源参与电力市场。考虑不同的可再生能源-通证兑换率，在同一时段进行对比可以看出，随着兑换率的增加，发电商增加可再生能源出力，因此，在相同的情况下，不同的兑换率对于激励发电商效果不同。因此在设计基于通证的激励机制时，需要设置合理的可再生能源出力-通证兑换率，来平衡发电商在联合市场的收益。

从图12、15、18可以看出，现货通证市场和远期通证市场的价格随着节点边际电价的不同而出现波动，发电商决策时都考虑了现货通证市场和远期通证市场的博弈情况，没有将所兑换的通证全部在一个通证市场上进行出售。且随着可再生能源出力-通证兑换率的提高，发电商在现货通证市场售出的通证数量逐渐减少。由上面的分析可知，在相同的情况下，发电商受到通证的激励，决策增加更多的可再生能源出力，因此发电商将获得更多的通证，考虑到通证市场价格波动的风险发电商也愿意保留通证在远期市场出售，来平衡自身在通证市场的收益。

从图13、16、19可以看出，无论何种可再生能源出力-通证兑换率，在考虑电价不确定性时，相比不考虑不确定性的情况，发电商增加了可再生能源的发电量。这是因为在考虑电价最差的情况下，发电商综合衡量可再生能源出力偏差造成的考核成本，发电商通过增加发电成本较低的可再生能源出力能够使得发电商的期望收益最大化。当通证兑换率越高时，由于可再生能源出力约束，可再生能源快逼近此时的出力上界值，因此可再生能源出力提升较低。

综上所述，本文设计的可再生能源通证激励机制能够有效激励含可再生能源的发电商参与电力市场，对于促进可再生能源发展具有重大意义。

5 结 论

随着可再生能源的消纳问题日益突出，可再生能源参与电力市场是促进消纳的有效手段之一，含可再生能源的分散式市场模式已成为未来可行的市场构架。本文从电力市场的结构出发，构建了包含电量市场和通证市场的分散式电力市场，以可再生能源和火电“打捆”的方式激励含可再生能源发电商参与电力市场，建立了含可再生能源的分散式电力市场出清模型，研究并分析了在通证激励机制下考虑电价不确定性的含可再生能源发电商行为决策问题。在未来的工作中，将会对通证激励机制在实际电力市场中的应用做进一步地详细研究。