束状孔当量球形药包爆破漏斗的模型研究

陈 何 万串串 王湖鑫

（1.矿冶科技集团有限公司，北京102628；2.国家金属矿绿色开采国际联合研究中心，北京102628）

自2002年开始，矿冶科技集团有限公司（原北京矿冶研究总院）进行了基于束状孔等效直径条件下的球形药包漏斗爆破大量落矿技术的试验研究与应用，包括束状孔爆破应力场的动态光弹试验、束状孔爆破等效应力场水下模拟研究等，初步揭示了束状孔爆破的机理特性和工艺应用条件，同时论证了依据束状孔等效直径概念及利文斯顿漏斗爆破理论实现束状孔当量球形药包漏斗爆破的可行性。该项爆破技术先后在冬瓜山铜矿、大红山铜矿、六苴铜矿等矿山进行了大规模应用试验，取得了良好的爆破技术经济指标［1-3］。

近年来，国内一些学者采用多种手段深入研究了束状孔爆破机理，并进行了多种工程效果分析评价。陈何等［4］基于束状孔当量球形药包爆破技术与束状孔变抵抗线爆破技术研发了束状孔大量高效采矿技术，在华锡集团铜坑矿细脉带矿体回采中得到了成功应用，并对该项采矿技术在矿山采空区安全高效治理、阶段大量连续开采、露天转地下平稳过渡等领域的应用进行了展望。史秀志等［5］对束状孔当量球形药包爆破技术在冬瓜山铜矿开展了现场爆破漏斗试验，得出等效束状孔爆破效果明显优于大孔爆破，并给出了相关设计参数。崔新男等［6］对束状孔和等效单孔爆破作用过程进行了数值模拟分析，结果显示束状孔爆破在爆破近区过粉碎程度低，中远区能量较大，整体爆破效果好。上述研究成果均未涉及束状孔当量球形药包爆破漏斗的模型分析，对于束状孔爆破作用机理未进行深入研究，无法定量化表征束状孔爆破作用效果。本研究通过引入高斯曲线漏斗试验模型，分析束状孔当量球形药包爆破的单位炸药爆炸释放能量、药包埋深、炸药能量利用率等指标，为束状孔爆破效果评价提供定量化表征方法。

1 爆破漏斗试验方案

本研究爆破漏斗试验方案包括当量大孔爆破漏斗试验、束状孔当量球形药包爆破漏斗试验等内容。

1.1 矿山岩石力学参数

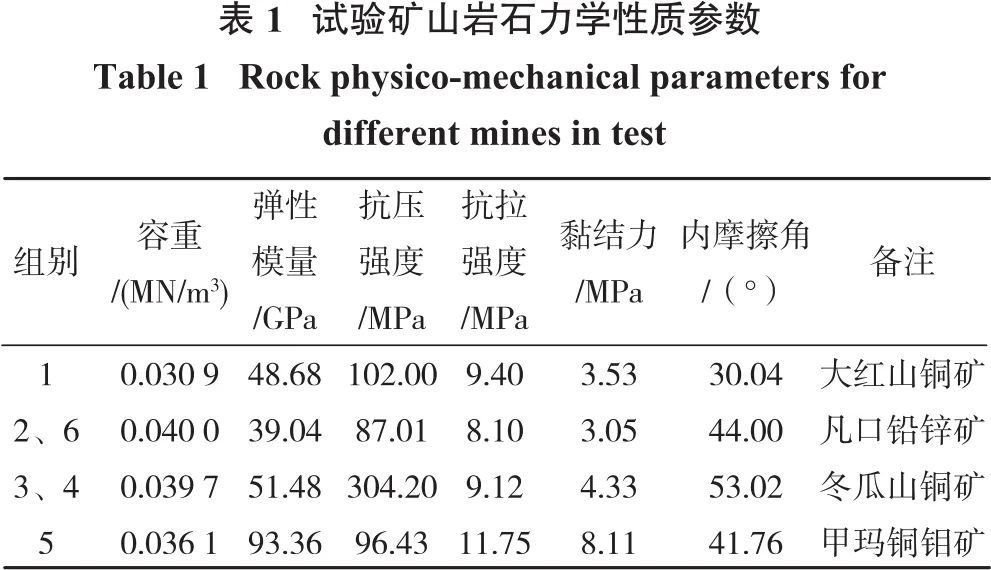
本研究分别在4座矿山开展了束状孔当量球形药包爆破漏斗试验，各矿山岩石力学性质参数取值见表1。

1.2 试验材料

束状孔爆破炸药选用矿山生产常用的乳化硝铵炸药、多孔粒状铵油炸药和膨化硝铵炸药等。乳化硝铵炸药爆速4 500 m/s，密度1.05～1.10 g/cm3；多孔粒状铵油炸药爆速2 800 m/s，密度0.9～0.93 g/cm3；膨化硝铵炸药爆速3 200 m/s，密度0.95～1.00 g/cm3。束状孔爆破试验材料见表2。

1.3 炮孔布置

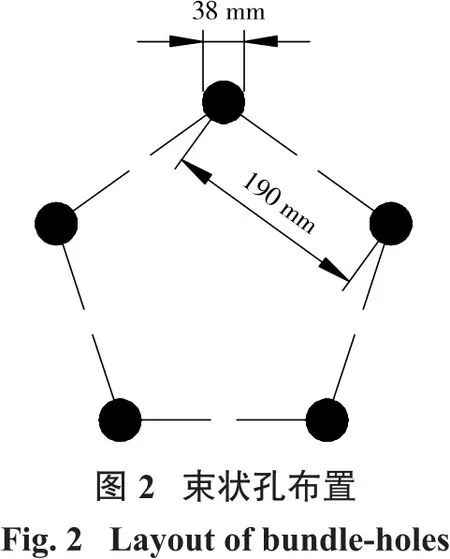
试验在巷道顶板或侧帮进行。束状孔孔径d0为38～45 mm，每束4～5个孔，孔间距190～225 mm。炮孔布置如图1、图2所示。

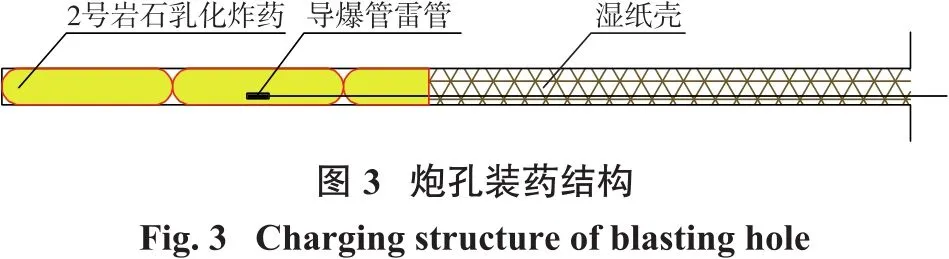
炮孔采用连续耦合装药，束状孔当量球形药包长度l=6D0（D0为当量大孔直径），设计采用不同药包埋深进行试验，装药结构如图3所示。

1.4 起爆网络

每个束状孔内均采用1段瞬发非电雷管起爆，于孔口处与2发电雷管捆扎一起，各束间电雷管串联，一次起爆。孔内炸药采用非电雷管直接起爆。

2 爆破漏斗试验结果

2.1 爆破漏斗试验

试验设计了1#～6#不同深度的束状孔。试验采用直径32 mm的药卷，单个药卷长20 cm，质量200 g。每个单孔共装2.5卷药，总长0.5 m，总质量0.5 kg。按设计的埋深将药包装入炮孔中，并填塞、封堵炮孔。爆破试验结果见表3。

爆破后采用三维激光扫描仪对漏斗形状进行了现场测量［7-8］，测量数据建模结果如图4所示。

本研究绘制的爆破漏斗体积V与药包埋深W的关系曲线如图5所示。由图5可知：爆破临界埋深LN=2.15 m，最佳埋深Wj=0.75 m，此时爆破所形成的漏斗体积最大，该漏斗体积为0.69 m3，由矿岩密度4 000 kg/m3、束状孔装药药量2.5 kg可算出，炸药单耗q=0.906 kg/t。

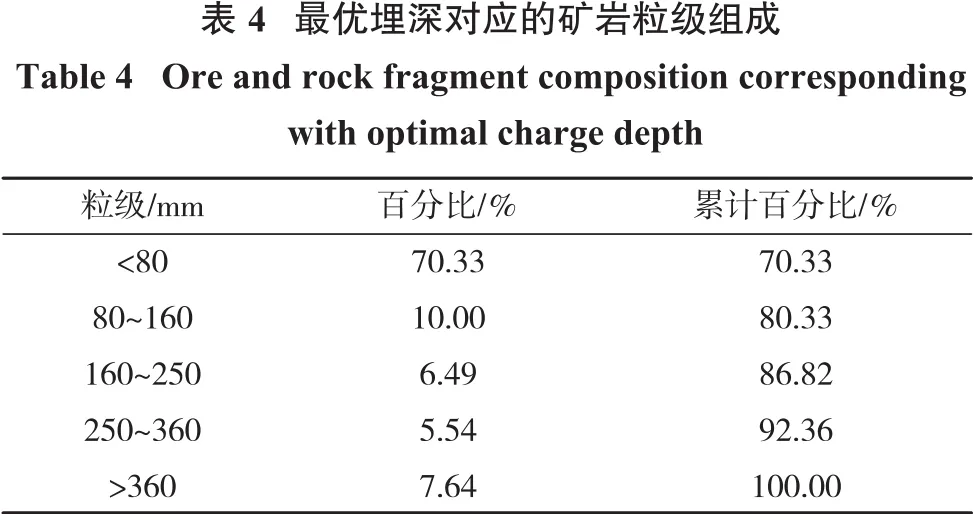
最佳埋深对应的爆落矿岩粒级组成见表4。

2.2 试验数据计算分析

药包埋深比计算公式为

式中，W为药包埋深，m；LN为药包临界埋深，m。

单位炸药爆破体积用V/Q表示，其中V为爆破漏斗体积，m3；Q为药包炸药量，kg。当药包埋深为0时，Δ=0，V=0。当药包埋深为临界埋深时，Δ=1，V=0。为了获得爆破漏斗全曲线，将药包埋深为0与药包临界埋深两个数据加入本研究试验数据中，如表5所示。

3 爆破漏斗模型与数据分析

3.1 束状孔当量球形药包爆破漏斗特征

与当量大孔集中药包爆破相比，束状孔爆破的主要特点在于，束状孔内各药包由于邻近布置，改变了药包形状、分布形式、装药结构等，从而改变了爆炸作用于岩体的应力分布［9-10］。束状孔爆破应力波为多峰值应力波，其爆破近区的爆破压力远低于当量大孔，过粉碎破碎岩石消耗的能量低，其破碎岩石形成的爆破漏斗体积较大。大量试验表明，束状孔爆破漏斗体积随埋深变化的基本规律仍与当量大孔一致。

当准静压力对新边界的作用大于岩石抗压强度，且应力波在边界的反射拉伸破坏半径与埋深相等时，爆破漏斗为正漏斗，爆破体积最大，埋深为药包的最佳埋深。随着埋深减小，表面逐渐出现漏斗状岩石破裂区，漏斗逐渐扩大，爆轰气体准静压力也参与到漏斗的形成过程中，在联合作用下，漏斗顶角扩大至90°，体积达到最大；当埋深进一步减小时，漏斗顶角变得越来越大，由于反射拉伸破坏导致岩石过快破坏，使爆轰气体短时间泄漏，准静压力有效作用能量下降，爆破漏斗体积变小。药包处于临界埋深时，应力波在边界的反射拉伸破坏半径为0。此时，炸药爆炸能量中的塑性波能量全部转化为弹性能量，被岩石全部吸收。

3.2 束状孔爆破漏斗模型

3.2.1 爆破漏斗试验曲线

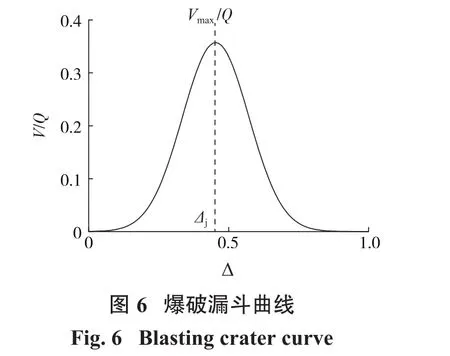
3.2.2 高斯函数拟合

假设随药包埋深变化的爆破漏斗体积变化为正态分布，则爆破漏斗曲线可用高斯函数［11-12］进行拟合：

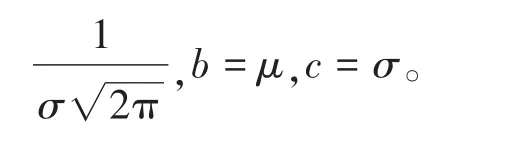
式（2）中，a表示高斯函数的极值，爆破漏斗拟合曲线中表示最大单位炸药爆破体积；参数b表示高斯函数的对称轴位置，曲线中表示药包的最佳埋深比Δj；c表示高斯函数曲线的陡峭程度，c越小表示曲线越陡，c越大表示曲线越平缓，曲线中表示炸药能量利用效率的集中程度。

在不同的埋深区间[ ]x1,x2内，高斯函数曲线的积分值代表该范围内破碎岩石的总量，反映不同爆破形式的炸药能量利用效率。

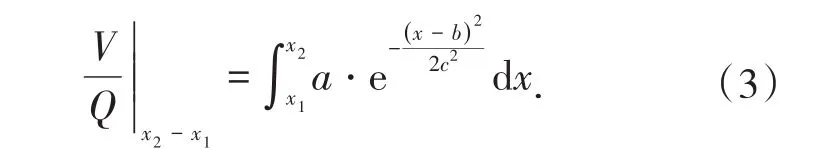
3.3 试验数据分析

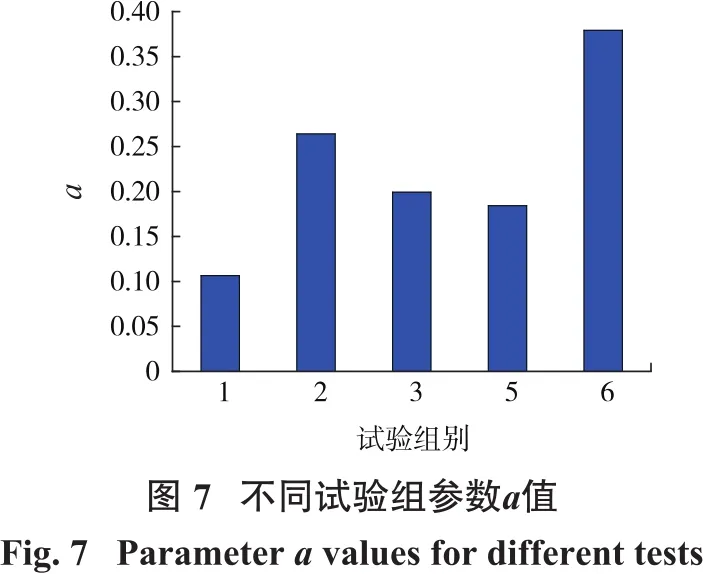
根据爆破漏斗试验数据，高斯函数曲线拟合参数见表6。

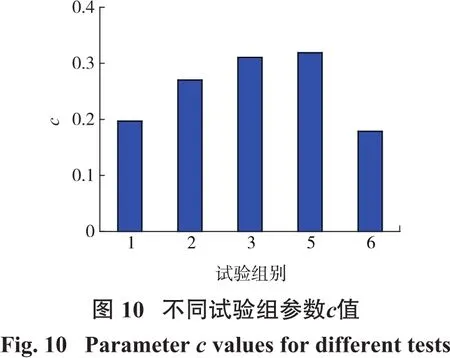
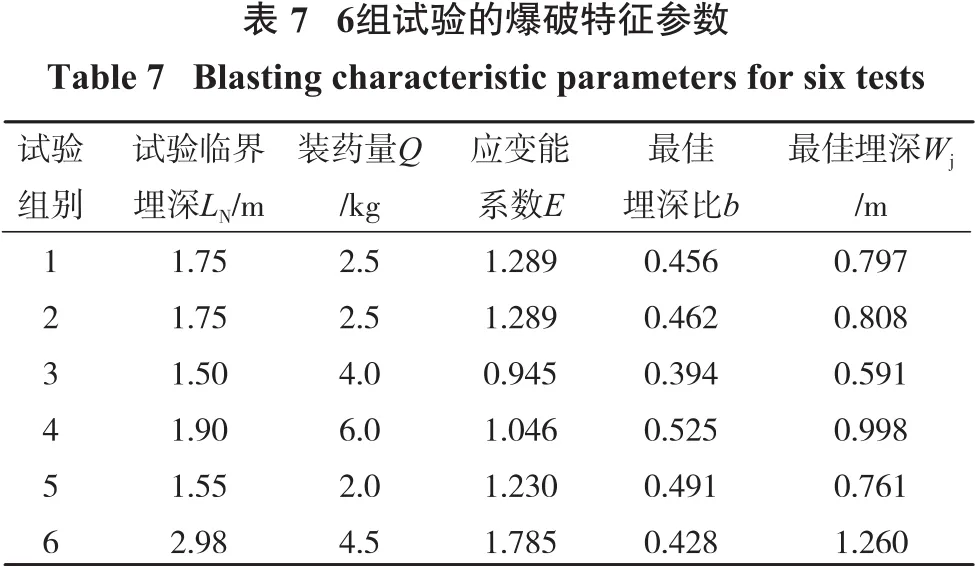
由表6可知：第4组试验值明显偏离其余5组试验值，主要是由于试验矿段较破碎，岩体力学参数变化较大所致，因此试验组别之间的分析不采用该组数据。

如图7所示，影响参数a的主要因素为单位炸药爆炸释放的能量及岩体性质；第2、第6组试验在相同矿山进行，第6组试验采用高能量密度炸药，a值最大；第2组试验采用普通乳化炸药爆破，a值偏小。

岩石抗拉强度σs与a值的关系如图8所示。分析该图可知：抗拉强度越低的岩石a值越大，可爆破性越好。

不同试验组别的参数b取值如图9所示。由该图可知：5组试验的最佳埋深比Δj为0.39～0.49。

参数c表征炸药爆炸能量的有效利用率，由图10可知：第6组c值最小，即束状孔爆破的约束条件更好，炸药能量利用效率更集中。

3.4 束状孔爆破最佳埋深参数计算

由漏斗爆破高斯函数模型（式（2））可知，当药包处于最佳埋深比b=Δj时，最大单位炸药爆破体积VmaxQ=a。文献［13］研究表明：药包埋深与炸药能量利用率之间存在比例关系［13］，通过爆破漏斗试验得出药包极限埋深，从而求出最佳埋深Wj：

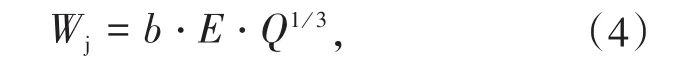
临界埋深计算公式为

从而有：

漏斗试验得到的爆破特征参数见表7。束状孔当量球形药包爆破的最佳埋深比b为0.394～0.525时，应变能系数E为0.945～1.785。

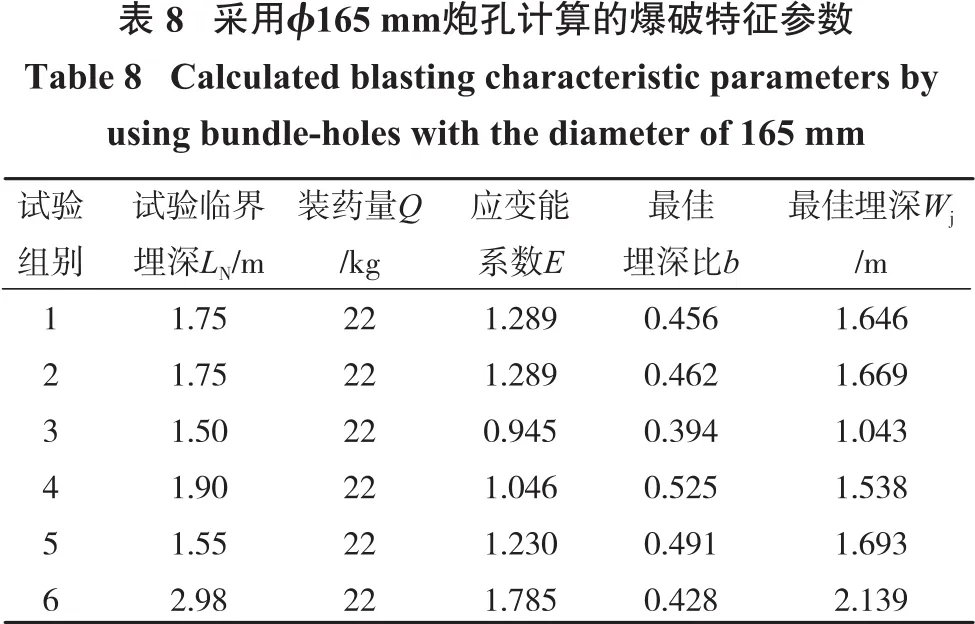
在相同的岩石、炸药条件下，不同炮孔数束状孔的爆破参数可由漏斗爆破高斯函数模型（式（2）、式（4）和式（6））计算。

1个ϕ165 mm炮孔（装药长度le＝0.99 m）的爆破参数计算结果见表8。

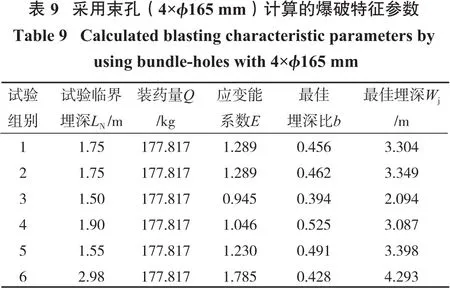
4个ϕ165 mm炮孔组成的束状孔（装药长度le＝1.98 m）计算的爆破参数见表9。

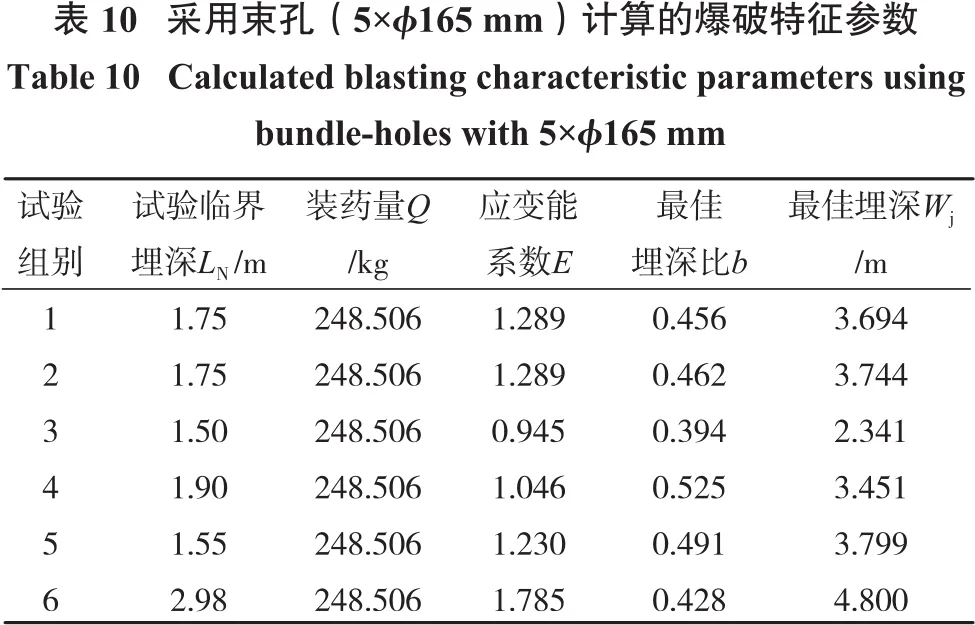
5个ϕ165 mm炮孔组成的束孔（装药长度le＝2.21 m）爆破参数计算结果见表10。

一束由n个炮孔组成的束孔的药包最佳埋深计算公式为

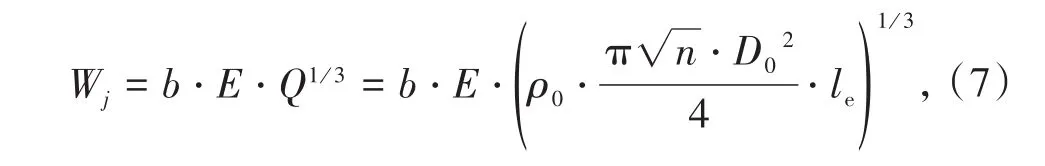
式中，ρ0为炸药密度，kg/m3；le为药包长度，m；D0为当量大孔直径，m。

当le=6D0，ρ0=1 000 kg/m3时，有：

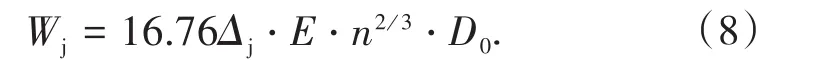
将上述测量方法在某矿山进行了现场应用，结果如图11所示。束状孔爆破后，采用三维激光扫描仪进行了精确测量，得到了每次爆破漏斗体积。针对不同埋深条件的束状孔爆破试验数据，采用高斯模型可拟合出爆破漏斗曲线，为进一步评价束状孔爆破效果提供了定量化表征方法。

4 结论

通过开展束状孔当量球形药包爆破漏斗试验，建立了束状孔药包埋深与爆破漏斗体积的关系模型，采用高斯函数对不同药包埋深比的爆破漏斗曲线进行拟合，得到了束状孔爆破漏斗的高斯函数关系式，通过定量化拟合爆破漏斗试验曲线，计算其特征参数，为科学计算束状孔爆破相关指标提供了有效手段。研究得到以下结论：

（1）通过不同埋深条件下束状孔当量球形药包爆破漏斗试验，建立了漏斗爆破高斯函数模型，分析了单位炸药爆炸释放能量、岩石抗拉强度、药包埋深、炸药能量利用率等指标对束状孔当量球形药包爆破作用的影响，为束状孔爆破效果评价提供了定量化表征方法。

（2）根据束状孔当量球形药包爆破漏斗试验及漏斗爆破高斯函数模型，开展了4个及5个炮孔组成束状孔的爆破参数计算，确定了束状孔爆破时药包最佳埋深，为束状孔爆破设计提供了技术参考。

（3）本研究提供了一种用于表征束状孔当量球形药包爆破漏斗特征的高斯函数模型方法，但对于精确化测量爆破漏斗体积需要进一步创新测量手段，提高测量精度，进一步提升束状孔爆破特征参数计算的准确性与可靠性。