基于CDEM的采空区稳定性及临界顶板厚度分析

王永增 王心泉 王 润 冯 春 曹 洋 孟磊磊 吴恩泽

（1.鞍钢集团矿业有限公司齐大山分公司，辽宁鞍山114000；2.中国科学院力学研究所，北京100190；3.中国科学院大学工程科学学院，北京100049）

地下矿产资源被开采出来后会遗留下采空区，采空区的存在改变了岩体的原有应力场，使得岩体的原有平衡被破坏［1-3］，易产生地表塌陷、地面沉降等问题，对露天开采的安全性存在巨大的威胁［4-6］。采空区顶板的临界厚度是开采过程安全性评价的重要指标，对采空区稳定性评价有着重要的意义。近年来，不少学者对此进行了深入研究。唐硕等［7］基于模糊物源理论，确定采空区稳定性的影响因素，建立了采空区稳定性评价模型，评价结果用关联度表示。柳小波等［8］结合第一强度理论提出了顶板厚度计算的新方法，采用Abaqus模拟分析了各因素对采空区顶板破坏的影响规律。姜桂鹏等［9］基于量纲分析法建立了采空区顶板稳定性判别的数学模型，结合有限元数值模拟分析，得到了稳定的临界厚跨比。唐胜利等［10］基于BP神经网络原理，结合采空区稳定性影响因素构建了BP神经网络模型，并对空洞型采空区进行了稳定性评价。王炳文等［11］综合理论分析和数值模拟结果，对遗留采空区群进行了稳定性级别评定。张瑞等［12］利用三维探测扫描设备建立了采空区三维数值模型，综合多种采空区稳定性评价方法对采空区进行安全分级。卢欣奇等［13］通过FLAC软件对近地表采空区进行数值模拟分析，提出了治理方案，并通过FLAC模拟分析对各方案的治理效果进行了对比。张敏思等［14］采用多种理论方法计算了不同跨度采空区顶板的安全厚度，并采用RFPA数值模拟软件对采空区进行模拟得到顶板出现初始损伤及失稳垮塌的厚度。周平等［15］依据尖点突变模型得到采空区在充填体荷载作用下的顶板厚度表达式。王志修等［16］采用理论计算和数值模拟手段研究了卢安夏露天铜矿地下采空区顶板的安全厚度。胡洪旺等［17］基于Ressiner厚板理论构建了理论分析模型，推导出顶板挠曲线方程及顶板最大应力表达式，并利用Matlab软件计算得到顶板厚度随坐标轴变化的三维曲线图。

现有的采空区顶板稳定性研究理论中，多将采空区顶板视为弹性梁进行近似处理，难以考虑岩石的材料性质对采空区稳定性的影响。同时多数研究只通过数值计算对采空区顶板进行规律性分析，缺少对采空区顶板临界厚度的定量分析。本研究从量纲分析出发，探讨与采空区临界顶板厚度相关的因素，借助连续-非连续单元法（Continuous-Discontinuous Element Method，CDEM）通过数值分析，找出影响临界顶板厚度的关键变量，得到临界厚度与相关变量之间对应公式，为评价采空区稳定性提供定量性的参考指标。

1 量纲分析

1.1 采空区临界顶板厚度影响因素分析

采空区临界顶板厚度的影响因素复杂，根据以往工程经验及采空区研究资料，综合考虑各方面的作用，本研究将影响因素分为几何形状因素、地层岩性因素及外力荷载因素［18-19］。

影响采空区临界顶板厚度Hc的自变量为：①几何参数为采空区长度a、宽度b和高度h；②材料参数有密度ρ、弹性模量E、泊松比μ、黏聚力c、内摩擦角ϕ、抗拉强度σt和剪胀角ψ；③静载荷F（假设载荷作用点位于采空区正中）；④重力加速度g（图1）。

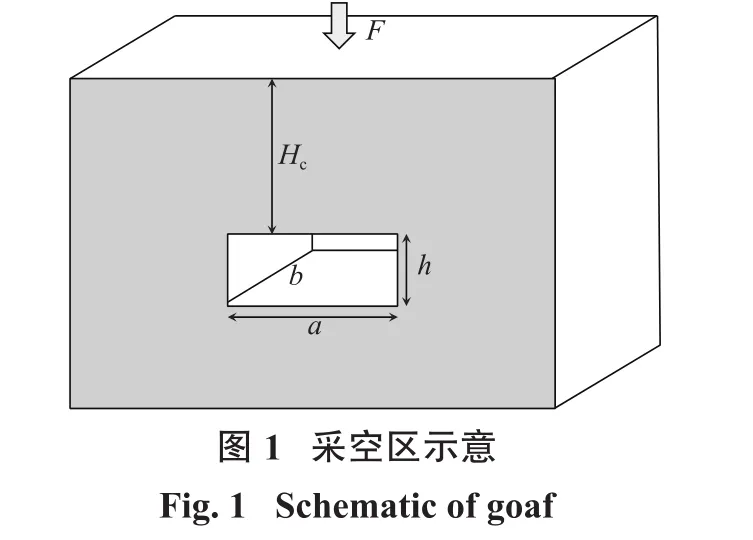
1.2 无量纲表达式建立

临界顶板厚度Hc与各影响因素之间的关系可表述为

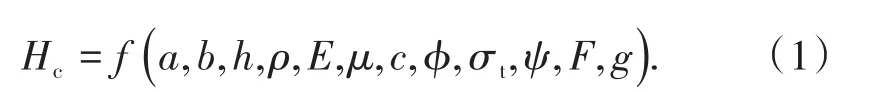
以密度ρ、重力加速度g、采空区长度a为基本量，建立的无量纲表达式为

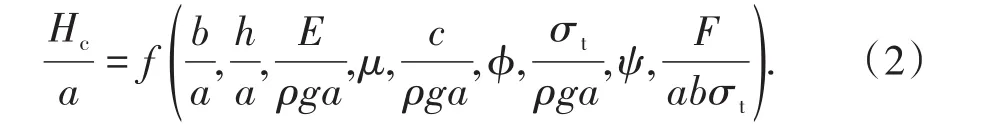
理论分析可知：弹性模量、泊松比对弹性变形有较大的影响，但对临界顶板厚度Hc影响不大，因此可以忽略；此外，采空区高度h仅对顶板垮落后的下沉距离有影响，对临界顶板厚度Hc无影响，因此也可以忽略。由此，式（2）可变为

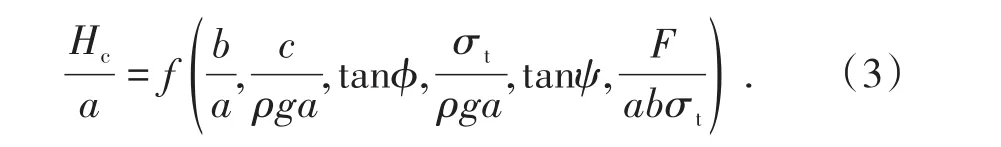
2 采空区稳定性影响因素

2.1 顶板安全系数主要影响因素

本研究采用连续-非连续单元法（CDEM）建立二维采空区数值模型，重点探讨采空区的几何参数及岩体物理力学参数对采空区稳定性的影响规律，并借助安全系数进行定量分析。由于采空区临界顶板厚度的影响因素众多，本研究采用多参数分析理论与方法［20-21］对参数进行灵敏度分析，进而给出顶板安全系数的主要影响因素。

计算时根据采空区的常见特征设立一组参数基础值，当研究某一个参数的影响时，其他参数取基础值，各参数基础值取值如表1所示。

根据工程中常见的采空区几何尺寸及采空区顶板力学参数的取值范围，确定采空区特征尺寸及采空区顶板力学参数的下限值及上限值。根据以往研究成果，表2中的参数对采空区安全系数的影响都是单调的，故首先研究极限参数下采空区顶板的安全系数，根据安全系数变化值分析参数的敏感性。采空区参数限值及对应的安全系数如表2所示。

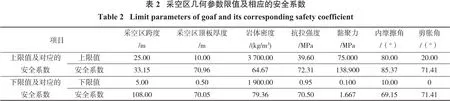
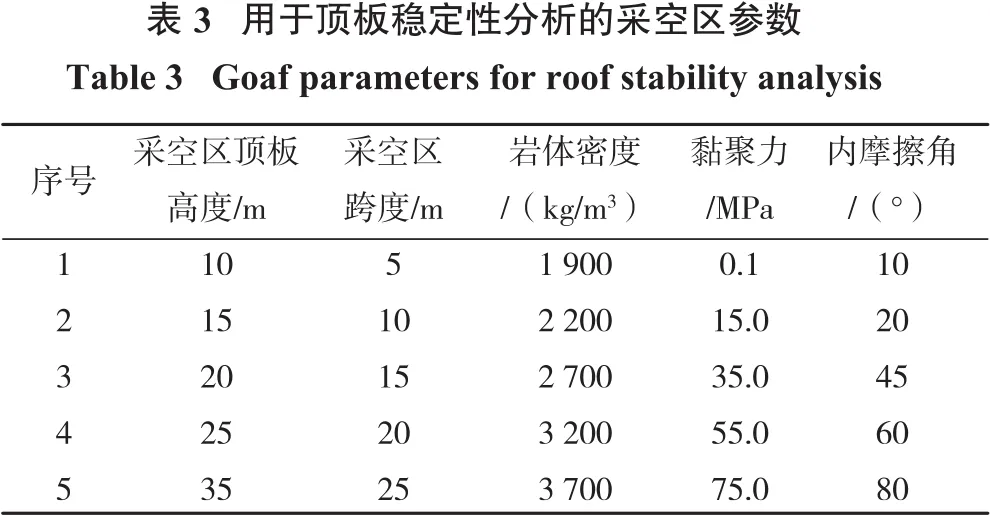
由表2可知：黏聚力对安全系数的影响最大，采空区跨度、岩体内摩擦角、岩体密度次之。因此，本研究重点研究不同顶板厚度下，采空区跨度、黏聚力、内摩擦角、岩体密度与空区顶板安全系数的对应关系。当研究某一参数对顶板稳定性的影响时，剩余参数取值为基础值。顶板稳定性规律研究时，各影响因素的计算参数取值范围在设定的基础值附近，不超过理论及工程上的合理取值范围，试验中各参数取值如表3所示。

2.2 顶板安全系数变化规律

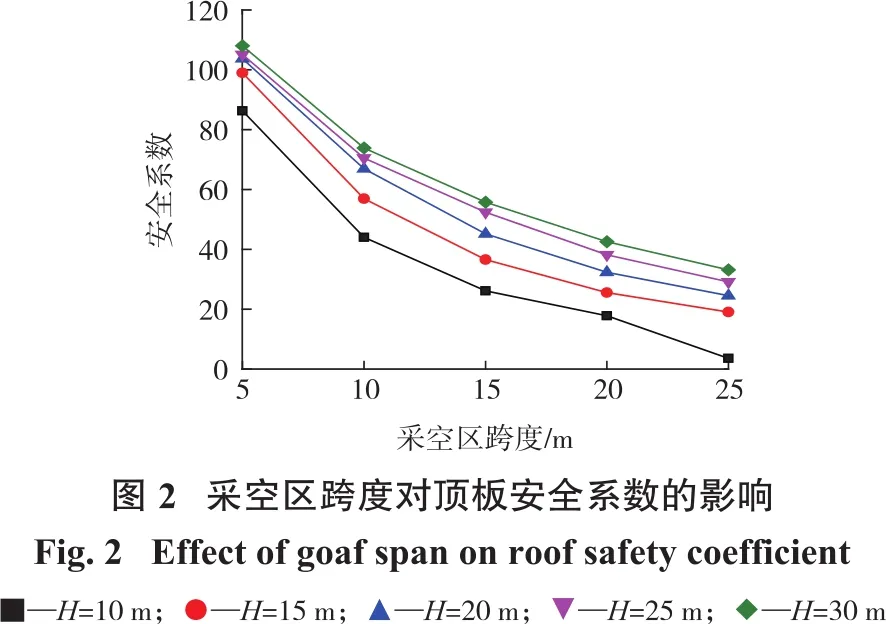
在不同的采空区顶板厚度H下，顶板安全系数与采空区跨度的对应关系如图2所示。分析该图可知：随着采空区跨度增大，安全系数逐渐减小，但减小趋势逐渐变缓；随着顶板厚度增大，安全系数逐渐增大，但增大幅度也逐渐变缓。

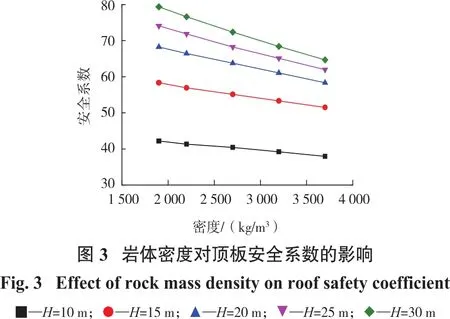
岩体密度对采空区顶板稳定性的影响如图3所示。由图3可知：随着岩体密度增大，顶板安全系数基本呈线性减小趋势；且随着顶板厚度增大，安全系数逐渐增大，但增大幅度逐渐变缓。

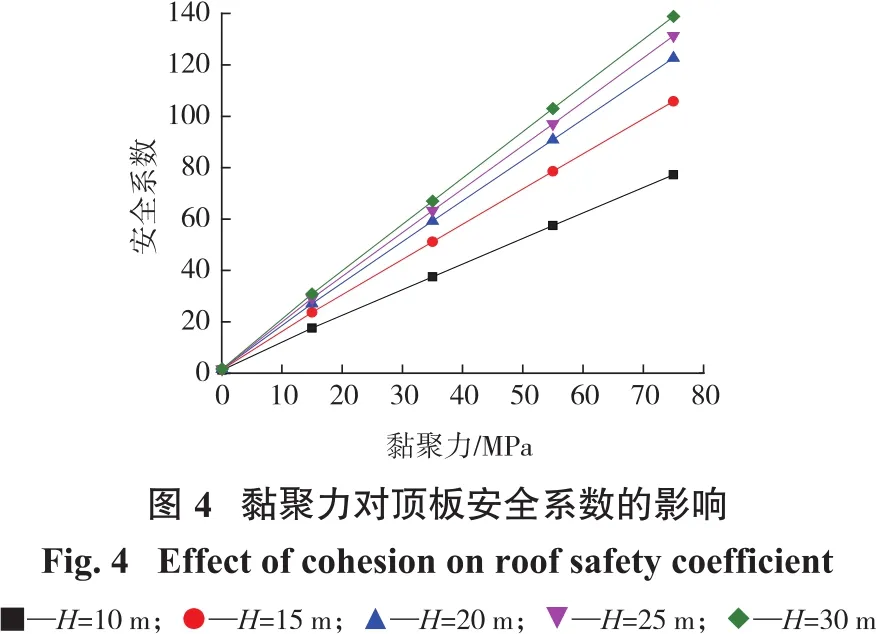
岩体黏聚力对采空区顶板稳定性的影响规律如图4所示。由图4可知：随着岩体黏聚力增大，顶板安全系数基本呈线性增大趋势；且随着顶板厚度增大，安全系数与黏聚力之间直线关系的斜率逐渐增大。

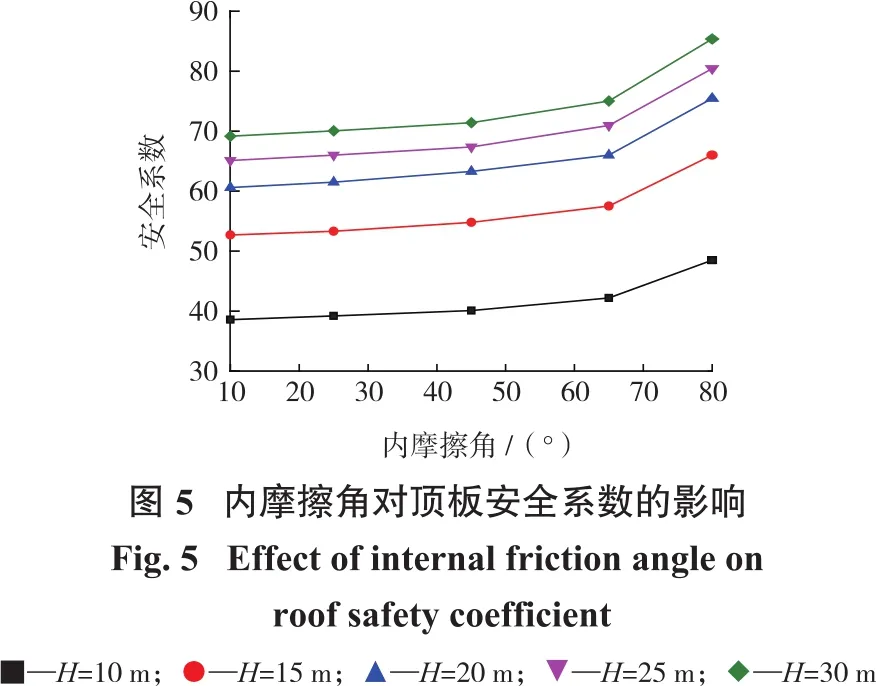
岩体内摩擦角对采空区顶板稳定性的影响规律如图5所示。由图5可知：随着岩体内摩擦角增大，顶板安全系数呈现非线性增大趋势；内摩擦角小于65°时，基本呈直线变化；大于65°时，安全系数有突然增大现象。总体上，随着顶板厚度增大，安全系数逐渐增大，但增大趋势逐渐变缓。

3 采空区临界顶板厚度分析

本研究借助连续-非连续单元法（CDEM）并采用二维模型及三维模型分别进行采空区临界顶板厚度分析。二维模型采用连续介质模型进行计算，单元模型为Mohr-Coulomb理想弹塑性本构模型；三维模型采用非连续介质模型进行计算，单元模型为线弹性本构模型，单元间的虚拟界面采用脆性断裂的Mohr-Coulomb本构模型。

3.1 三维模型下无量纲参数间关系

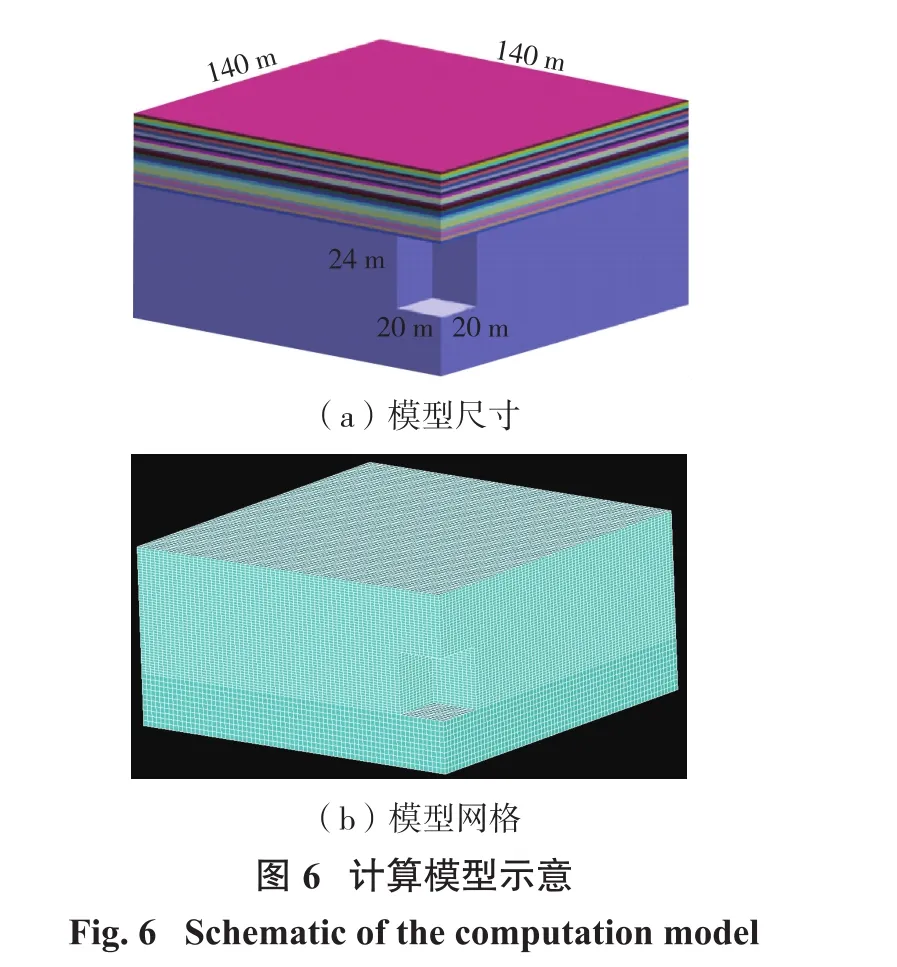
首先探讨采空区长度及宽度的影响，建立的三维模型外边界尺寸为140 m×140 m×64 m（长×宽×高），采空区高度为24 m，本研究假设模型长度a和宽度b一致，如图6所示。单元模型采用线弹性模型，单元间的边界采用脆性断裂模型。计算过程中的基础参数取值如表1所示。

无量纲临界厚度与无量纲强度间的关系如图7所示。由图7可知：随着无量纲强度增加，无量纲临界厚度迅速减小，两者关系可用下式进行表示：

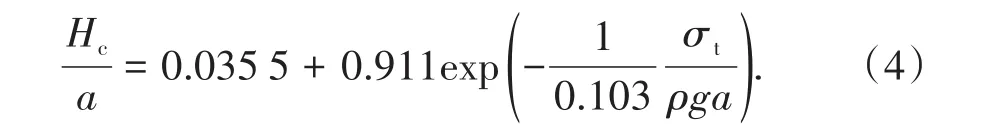
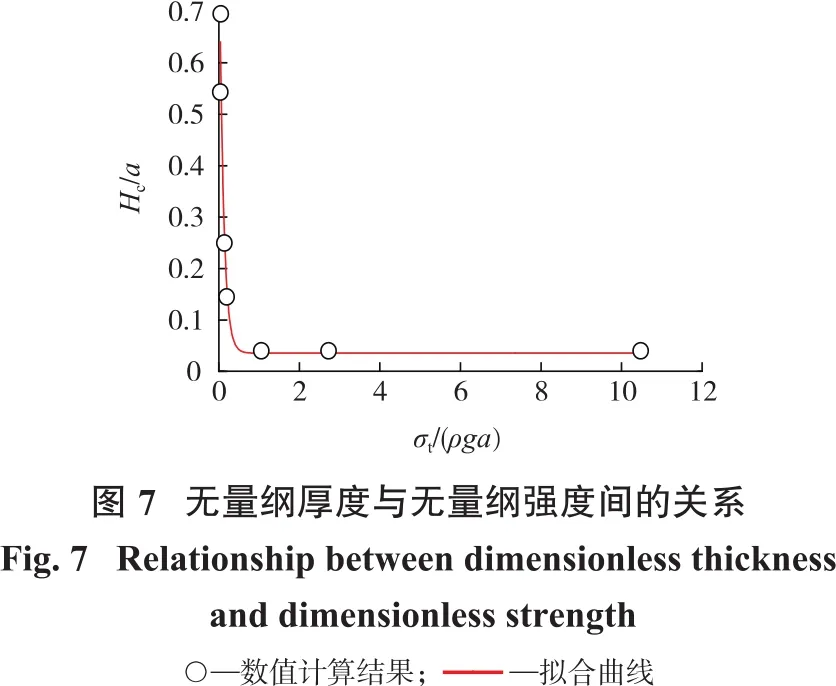
3.2 二维模型下无量纲参数间关系

本研究构建了长100 m、高50 m的二维数值模型，研究无量纲临界高度与无量纲强度间的对应关系。由于模拟的是二维平面应变问题，因此宽度b为无限大。本研究采用理想弹塑性模型进行分析，计算过程中的基础参数取值见表1。

共设计3类工况，工况1：设定临界高度Hc为5 m，采空区高度h为5 m，采空区长度a分别为10、20、30、40、50 m，通过二分法求取对应的强度值；工况2：设定临界高度Hc为10 m，采空区高度h为5 m，取采空区长度a分别为10、20、30、40、50 m，通过二分法求取相应的强度值；工况3：设定临界高度Hc为15 m，采空区高度h为5 m，取采空区长度a分别为20、30、40、50 m，通过二分法求取相应的强度值。

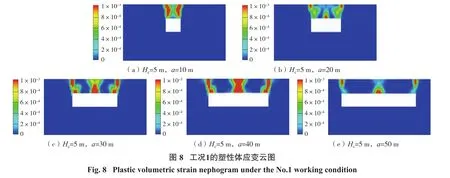
第1类工况下，临界失稳时的塑性体应变云图如图8所示。由图8可知，当Hc/a较大时，采空区顶板主要发生沿着侧壁切落；随着Hc/a减小，采空区顶板侧壁易发生拉剪破坏，采空区中部也易发生弯拉 破坏。

基于上述3种工况的模拟结果，得到了无量纲临界高度与无量纲强度之间的关系曲线，如图9所示。由图9可知：尽管3种工况下，各类参数差异较大，但在无量纲的表述下，均可用一条曲线进行表述，采用指数衰减型函数进行拟合，得到的无量纲临界高度与无量纲强度的关系式为

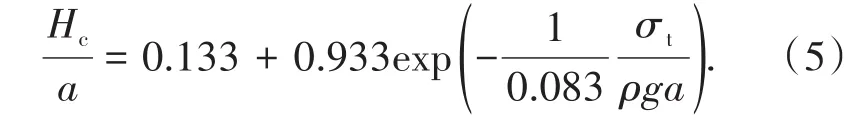
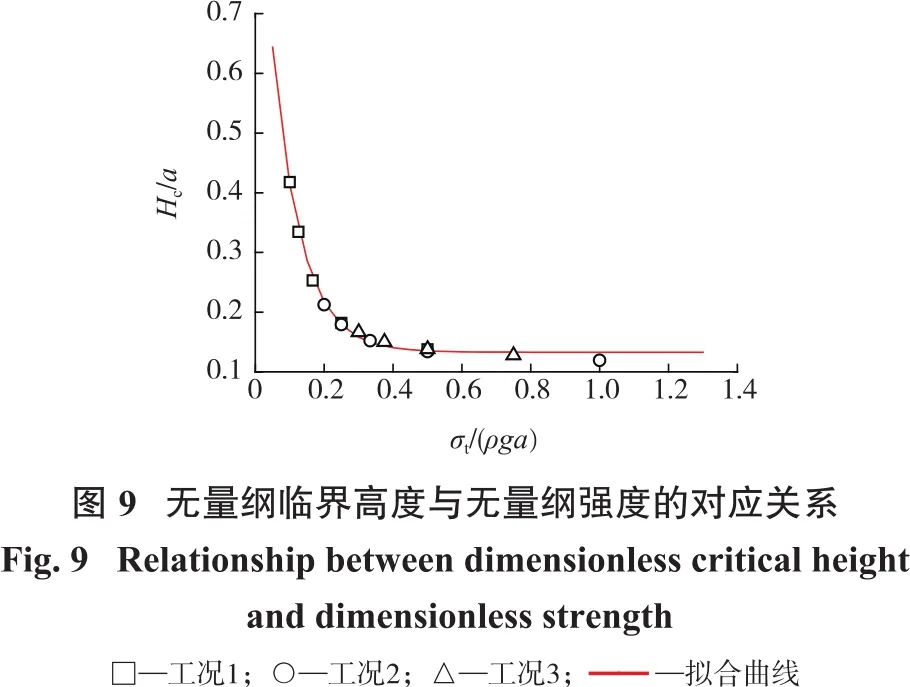
综合分析式（4）、式（5），可得无量纲高度与无量纲强度之间的关系可表示为

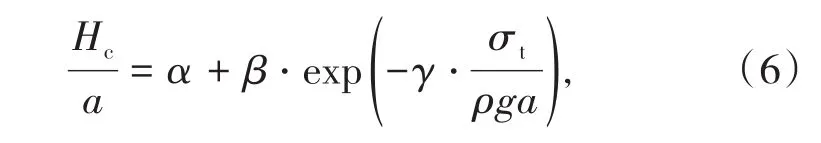
其中，α、β、γ为待定系数。

需要指出的是，式（4）与式（5）的系数有所差别。一方面是由于两个模型采用了不同的计算模型及计算本构模型；另一方面是由于二维模型忽略了采空区第3个方向尺度对采空区顶板稳定性的影响。

4 结论

（1）借助量纲分析手段，分析了采空区临界顶板稳定性的主要影响因素，得到与采空区顶板厚度相关的无量纲参数。选取黏聚力、采空区跨度、岩体内摩擦角、岩体密度为参数，借助CDEM数值分析方法，通过改变各参数的取值计算了采空区顶板的安全系数。并对二维、三维两种模型下无量纲临界高度与无量纲强度间的对应关系进行了研究，得到了无量纲临界高度与无量纲强度间的函数表达式。

（2）弹性模量、泊松比对临界顶板厚度影响不大，采空区高度对临界顶板厚度无影响；黏聚力对安全系数影响最大，采空区跨度、岩体内摩擦角、岩体密度次之。在只改变某一参数取值的情况下进行分析发现，随着采空区跨度增加、岩体密度增加、黏聚力减小、内摩擦角减小，顶板安全系数呈减小趋势；随着顶板厚度增加，安全系数增加，但增加趋势变缓；随着无量纲强度增大，无量纲的临界顶板高度基本呈指数衰减型的下降趋势。

（3）在进行二维及三维无量纲临界高度与无量纲强度关系表达式计算中，由于两种模型所采用的本构模型有所差别，且二维模型忽略了采空区第3个方向尺度的影响，导致两种模型虽然关系表达式一致，但在拟合公式的系数取值上存在一定的差异。在下一步工作中，可考虑改变模型本构，或对同一模型改变计算参数，研究表达式系数是否发生变化，再做进一步的研究。