基于改进α-shape算法的三维点云树冠体积计算方法

程 钢 王敬宇 杨 杰 赵宗泽 王 磊

(1.河南理工大学测绘与国土信息工程学院，焦作 454000；2.河南理工大学教务处，焦作 454000)

0 引言

森林是重要的生态与经济资源，包含了地球上约80%的植被生物量，对全球碳循环平衡具有非常重要的意义[1]。随着三维绿量[2]、冠积指数[3]等植被生物量统计参数概念的提出，三维树木因子的测定也变得愈发重要。树冠作为树木的重要组成部分，其体积参数的确定对森林生物量和三维绿量的统计分析具有重要作用。

传统的树冠体积量测方法[2-5]通过构建树冠体积预估方程进行量测，这种方法要考虑树种等因素的影响，其作业周期长、拟合形状差，测量精度很难保证，易造成计算结果不稳定、不准确等方面的问题。近年来，三维激光扫描技术已逐渐被应用到逆向工程[6]、文物保护[7]以及传统测绘[8]等领域，该技术可以在不接触物体的情况下对物体进行远距离测量，这为无损、快速、准确地量测树冠体积提供了契机。基于激光点云数据进行树冠体积计算的方法主要分为基于内部结构的树冠体积计算和基于外部轮廓的树冠体积计算两类。第1类计算方法，如文献[9-10]提出以固定的体元来模拟不规则树冠形状的体元模拟法，该方法对于浓密程度较高的树木由于遮挡原因会导致其利用三维点云数据构建的结构内部产生“空洞”现象，使测算结果相较于真值偏小。第2类计算方法，如文献[11]通过改进Delaunay算法机制，采用一种基于空间分割分块优先机制的三角网表面重建算法来提取树冠三维信息，具有较好的稳定性;文献[12]通过提取树冠冠体边缘点云，应用不规则三角网TIN计算冠体体积，由于每次提取的轮廓点仅有4个，故树冠体积计算结果不够准确;文献[13]将树冠分割为多个不规则的台体，但是将每个点云切片的横截面看作圆形或椭圆形，导致计算结果偏差较大;文献[14]对文献[13]中的台体法进行改进，通过计算每个树冠点云切片的凸包面积来求取台体体积，但计算结果仍有较大偏差;文献[15]运用三维凸包算法计算树冠凸包体积，由于未考虑树冠边缘间的空隙，故计算结果较真值偏差仍较大。

总的来看，体元法基于树冠内部结构计算树冠体积，有利于消除树冠内部无效体积，对于内部结构遮挡较少的稀疏枝叶树冠体积计算有一定优势，但对于枝叶较为浓密的树冠，由于缺少树冠内部点云数据，其计算结果往往不准确。因此，由于遮挡的缘故，体元法通常存在树冠体积低估的问题。台体法将三维树冠体积计算转换为多个二维切片面积计算，使其可以在充分利用树冠外部几何特征的基础上来求解三维树冠信息，是一种简单、快速、有效的树冠体积量测方法，其准确度除与树冠内部结构有关外，最关键的步骤在于台体外轮廓的精确计算。为了提高台体法的准确度，文献[16]提出了一种基于过滤三角网的树冠边界精确提取算法，对最优分层间距与过滤阈值进行了讨论，在考虑树冠外部空隙的情况下得到更为准确的树冠体积；文献[17]将边长阈值作为圆直径，在切片凸包的基础上搜寻“疑似边界点集”中与直径端点组成最大角的点作为新边界点，但未对边长阈值做进一步讨论。上述2种方法均通过设置固定边长阈值来消除树冠边缘存在的空隙，阈值过小，容易使整个切片碎片化，阈值过大，则会高估切片面积。考虑到动态阈值对于点云外轮廓形状描述的重要性，本文在α-shape算法[18-22]的基础上，借鉴三角网生长算法的思想[23-26]，提出一种考虑边界点云密度的动态阈值改进α-shape算法，以期提取更为准确的点云切片边界，并利用台体法的基本思想获取更为准确的树冠体积。

1 研究方法

1.1 台体法计算树冠体积

台体法计算树冠体积是把单棵树木整个树冠从下到上看作是由许多个台体和一个锥体所组成的几何体，如图1所示，通过对树冠点云数据基于高程进行切片并利用离散化格林公式求解每个切片面积S(图2)，进而计算出每个台体体积，然后将这些台体和锥体体积进行累加计算，即可算出整个树冠的体积。计算公式为

(1)

(2)

式中m——端点数量

(xk，yk)、(xk+1，yk+1)——第k、k+1个端点的平面坐标

Si、Si+1——第i、i+1层点云切片面积

n——切片数量

hi——相邻切片之间的间隔

hn+1——圆锥体高

V——树冠体积

计算过程中，点云切片面积的准确性至关重要，直接影响到后续树冠体积的计算，合理、准确地求取树冠点云切片面积成为台体法计算树冠体积的关键问题。

1.2 改进α-shape算法

α-shape算法作为经典的边缘探测算法之一，最早是由EDELSBRUNNER等[18]提出并被用于获取散乱点集的轮廓，本质上使用该算法所获取的图形为欧几里得空间中点集三角剖分的子集。文献[19]通过引入加权思想来控制点集中每一个点对周围点的影响力进而实现捕捉不同层次的局部空间特征，使得加权α-shape算法被广泛应用到局部特征提取领域，文献[20-21]均采用这种加权算法来实现对局部特征图形结构的探测。文献[27]通过计算检测点的k个邻近点平均距离和增设调节因子，自适应设置滚动圆半径α，但未考虑实测点云中激光扫描噪声和散乱点云点间距离散程度对α的影响。在提取树冠散乱点云轮廓方面，文献[28]通过使用α-shape算法获取了树冠体积并对结果进行了验证，但其获取轮廓的α是固定的，理论上仍存在提升树冠体积精度的空间。

二维空间中，α-shape算法可以想象成一个半径为α的圆在一堆无序点集P中进行滚动，当α足够大时，这个圆不会滚动至点集内部，此时的滚动痕迹即为该点集的边界[27]，如图3所示。本文将α-shape算法运用到点云切片外轮廓的获取，根据不同切片的点云结构，动态设定α。

根据文献[18]可知，当半径α趋于无穷小时，点集P中的所有点都有可能是边界点；当半径α趋于无穷大时，会形成一个包含点集P中所有点的凸包。理论上，存在一个阈值αb，当α≥αb时，其所形成的边界多边形可以包含点集P中的所有点。

本文通过迭代方式来找寻每个点云切片的阈值αb并获取该阈值下切片外轮廓多边形的面积。迭代公式为

αi+1=αi+Δα(i=1,2,…,n)

(3)

式中αi、αi+1——第i、i+1次迭代时圆的半径

Δα——迭代步长i——迭代次数

设树冠点云位于空间直角坐标系OXYZ中，OZ轴为高程轴。对树冠点云基于高程进行等间距切片处理，设其中一个点云切片的点集为D，则改进α-shape算法构建切片外轮廓多边形及求取面积的流程图如图4所示，具体如下：

(1)输入点云切片并设置初始α。

(2)构建邻域点集。将点集D投影至XOY平面，获取投影点集P中每一个点Pi的半径为2α的圆形邻域内的点集，其中i=1,2,…,n。为了提高其查询速度，本文借助了kd-tree结构来获取点集P中每一个点的邻域点集。

(3)设置边界初始点。由凸包性质可知，点集中任意一个凸包极值点均为该点集的边界点，为了便于获取可以将初始点设置为OX或OY方向上其中一个极值点即可，本文以OY方向上的最小值点PyMin为例，将其设置为初始边界点并加入到边界点集L中。

(4)获取整个切片的边界点集L。包括以下几个步骤：

①寻找下一个边界点。以当前边界点Li为基础，从其邻域点集Ni中选取任意一点n1，求出过点Li和n1且半径为α的两个圆o和o′；遍历点集Ni，依次判断邻域中其他点是否落入圆o和o′内部，如果存在一个不包含其他邻域点的圆(“空圆”准则，见图5)，则可以判断出点n1是点集P的边界点；对Ni内下一点重复上述过程，直至对Ni内所有点均使用“空圆”准则判别之后，统计其边界点的个数。

其中，初始点PyMin(L1)较为特殊，该点在寻找下一个边界点的过程中不需要统计其邻域内的边界点个数，只需要在NyMin中找到一个符合“空圆”准则的边界点即可执行步骤①，反之，如果一个边界点也找不到，则跳转至步骤(5)。

②判断边界点的唯一性。如果新找到的边界点有且仅有1个，则执行步骤③。如果新找到的边界点个数为0或多于1个，则跳转至步骤(5)，如图6a中，边界点7的邻域点集为空，新边界点的个数为0，边界无法回到起始点。图6b中，边界点3存在2个新边界点，边界出现2个可能的走向。图6这2种情况均说明当前阈值无效，需要更新α。

③判断唯一边界点是否为初始点。如果该边界点为初始点PyMin(图7)，则执行步骤④；反之，则将该边界点添加至点集L中，并执行步骤①。

④判断点集L是否包含点集P中的极值点。获取点集P中多个方向上的凸包极值点[29]，如图8a所示，根据文献[18]可知，相同点集下，该点集的凸包极值点亦是其边界凹包的极值点，故这些极值点一定为点集P的边界点。如果点集L未包含这些极值点，则该凹包仅仅为点集P的一个局部凹包，如图8b所示，则跳转至步骤(5)；反之，输出相应α值下的凹包并执行步骤(6)，如图8c所示。

(5)更新α并判断α是否达到终止条件。利用式(3)迭代更新α，之后将α与迭代阈值αmax相比较，如果大于αmax则停止迭代过程，输出一个包含点集P的凸包面积；反之，执行步骤(1)重新设置α。设置终止条件的原因在于：一方面，当α过大时，提取的边界形状趋于凸包，另一方面，可以避免程序陷入死循环。

(6)求解切片外轮廓多边形面积。利用离散化格林公式求解出切片外轮廓多边形面积的绝对值并输出，则整个边界提取过程结束。

最后，将整个树冠的所有点云切片均重复步骤(1)～(6)以获取其相应的切片外轮廓面积，求取对应的台体体积，进而通过累加求出更为准确的树冠体积。

2 分层间距与迭代步长的确定

2.1 树冠点云获取

本次实验研究区域为某校园内，选择晴朗天气采集树木点云数据，采集平台为Leica公司MS60型全站仪，扫描分辨率设置为0.01 m×0.01 m(与仪器激光发射中心某个距离的平面上，点云点间距在水平和垂直方向上均为0.01 m)，每秒测量3 600个点。选取校内14棵树进行扫描，获取树木点云数据后，对数据进行去噪和滤波处理，仅留下纯粹的树冠点云数据，如图9所示。算法实验在一台CPU为Intel Core i5-9300H、频率为2.4 GHz的便携式计算机上进行，开发平台为Matlab R2018a，α的初始值设置为0.01 m。

2.2 分层间距及迭代步长

使用改进α-shape算法计算树冠体积时，不同的迭代步长与树冠分层间距会直接影响树冠体积的计算效率与准确度，并且考虑到方法的实用性等因素，需要为改进α-shape算法确定最优的迭代步长以及分层间距。由微积分原理可知，树冠分层间距越小，使用该方法计算的树冠体积越准确。因此，将迭代步长为0.01 m、分层间距为0.1 m时的计算结果作为体积参照。为了消除不同树木之间计算时间与体积的差异，更为合理表征方法的计算效率与准确度，本文对不同树木样本的树冠体积与计算时间进行归一化处理，计算公式为

(4)

(5)

式中nt、nV——计算时间、树冠体积归一化值，nt越小表示计算效率越高，nV越大表示体积损失越大

t、Vα——使用改进α-shape算法计算单木树冠体积所用时长与体积

t0、V0——迭代步长为0.01 m、分层间距为0.1 m时所用时长和体积

采用不同迭代步长和分层间距对样本数据进行实验和统计，结果如图10所示。分析迭代步长对运算时间的影响及其造成的体积损失(图10a、10b)可知，当迭代步长Δα约为0.1 m时，计算效率的提升效果开始趋于缓和。考虑到随着迭代步长的增大，树冠体积损失也在增加，因此迭代步长Δα=0.05 m是一个较为理想的选择。在Δα=0.05 m的基础上，分析分层间距对时间和体积的影响(图10c、10d)可知，当分层间距Δh=0.2 m时，树木样本体积损失情况与Δh<0.2 m时的体积损失情况相当，并且其计算效率亦有显著的提升，故选择分层间距Δh=0.2 m。

对样本树木树冠体积计算的时长和体积进行统计和分析，见表1。分析表1可知，对女贞树2来说，采用选定的Δα与Δh时，体积V1比V0仅损失了1.360 7%，而时间仅为原来的11.851 3%，运算效率大大提升。对白杨树3来说，采用选定的Δα与Δh时，体积V1比V0仅损失了2.512 6%，而时间为原来的29.080 2%，运算效率明显提升。体积损失最高的是银杏树3，V1比V0损失了9.167 3%，时间为原来的21.845 9%，运算效率亦有明显提升。可见，在V1与V0的相对误差不超过9.167 3%的情况下，改进α-shape算法的用时仅为参照数据用时的11.460 6%～31.581 9%，显著提高了方法的运算效率和实用性，可以满足树冠体积测算的实际需求。

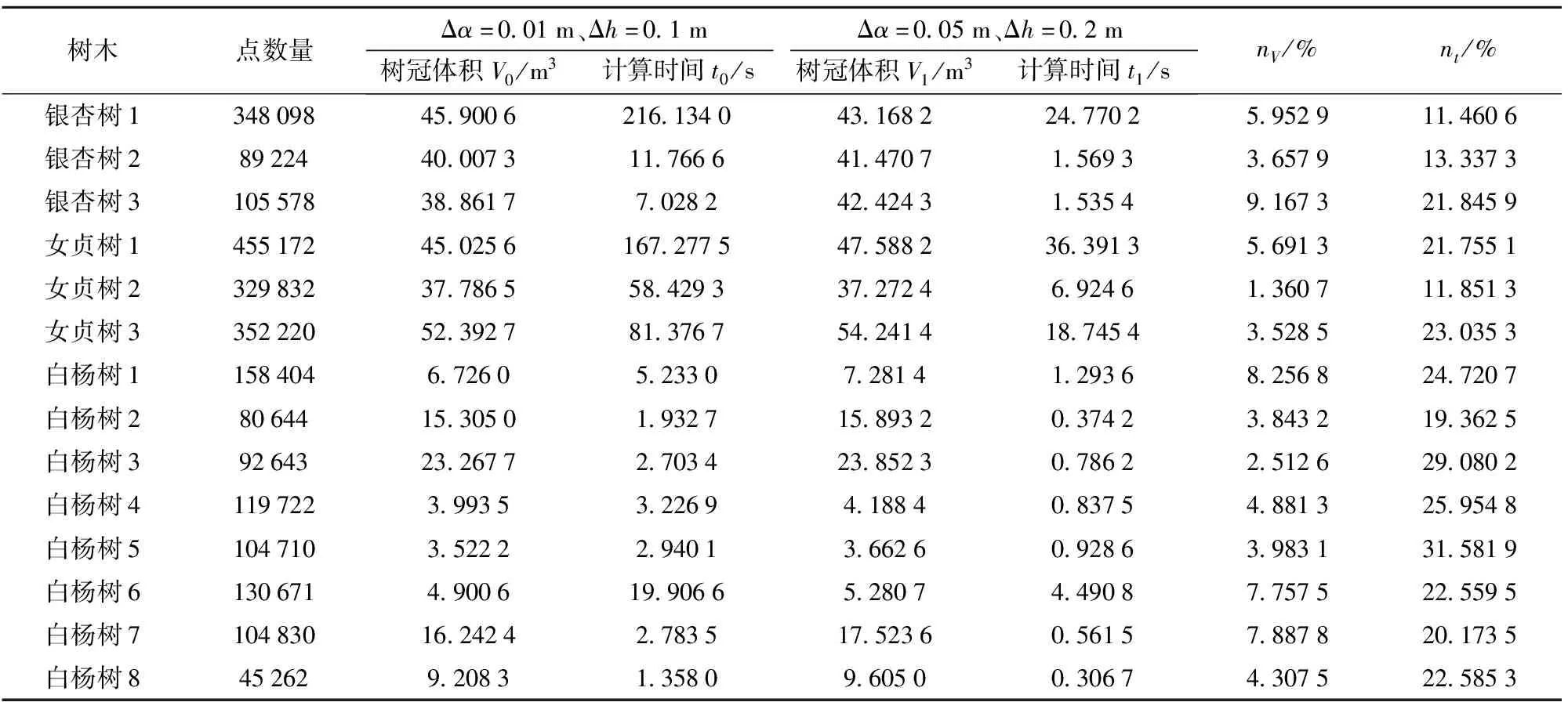
表1 树冠样本计算结果

3 实验结果与分析

3.1 树冠体积计算

分别使用体元累加法、Graham算法[14]和改进α-shape算法对所有树冠样本进行体积计算。参数设置方面，将改进α-shape算法的初值、迭代步长、分层间距、最大迭代阈值αmax分别设置为0.01、0.05、0.2 m、2；Graham算法的分层间距亦设置为0.2 m；参照文献[9]，本文对不同体元边长与体积增幅G之间的关系进行比较分析，从图11可见，当体元边长为10 cm左右时，体积增幅已趋于稳定，故将体元累加法中的体元边长设置为10 cm(数据获取方法同3.2节)。

(6)

式中Bi、Bj+1——体元边长为j、j+1时所计算的树冠体积

Gj——体元边长为j+1与j的树冠体积比值

将体元累加法、Graham算法和改进α-shape算法所计算出的树冠体积分别记为v0、v1和v2，结果如表2所示。

通过对不同树种不同方法获得的单木树冠体积(表2)进行分析，可以得出以下规律:

(1)对于枝叶密度稀疏的树冠(如银杏树1～3)，v1、v2相较于v0均偏差较大，存在高估现象，v2相比于v1更接近v0。分析原因在于，对于枝叶密度稀疏的树冠其内部的空隙可以被体元法更好地识别和去除，体积明显小于使用外轮廓进行体积估算的方法；由于Graham算法没有顾及到树冠边缘的空隙问题(图12)，本文算法相较于Graham算法所计算的结果v1会更为准确。

(2)枝叶茂密的情况下(如女贞树1～3、白杨树1～8)，3种方法得到的树冠体积更为接近。分析表2可知，v2恰好处于v0与v1之间，表明Graham算法的高估问题仍然存在，改进α-shape算法虽然略高于体元累加法，但相较于Graham算法更接近于体元累加法。分析原因在于，对于枝叶密度较高的树冠，体元法对于内部空隙的去除作用减弱。

表2 不同方法计算树冠体积

(3)通过表2可知，计算不同样本树冠体积时，求得了不同的α，说明本文方法对不同树种树冠的适用性较好。

综合分析来看，树冠体积计算准确度与树冠自身的枝叶结构关系紧密。本文算法可以适用于不同树种的树冠，无论是低密度还是高密度树冠，其结果相对于Graham算法可以去除凸包边界带来的高估问题，相对于体元累计法则更有利于树冠总体占用空间的计算。

3.2 改进α-shape算法稳定性测试

计算结果的稳定性是衡量一个算法好坏的重要指标，从样本数据中任意选取一个树冠样本进行算法稳定性测试。对原始点云数据经去噪滤波处理后，进行均匀抽稀。抽稀过程以树冠点云的立方体包围盒为基础，通过构建不同大小的正方体体元，保留体元内距离体元几何中心的最近点，剔除体元内其他点。使用这种方式可以将原始点云分别抽稀为分辨率为1～10 cm的树冠点云(分辨率k表示每个边长为k的体元内仅保留不多于1个激光点)，用以测试不同算法计算树冠体积的效果。对实验结果进行归一化处理，即

(7)

(8)

式中Kv、Ks——抽稀后树冠样本的体积相对误差和抽稀后点云占比。Kv越大则体积损失越大；Ks越小，则表示抽稀后剩余点云数据占原始点云数据比例越少

Fk、F1——点云体元边长为k、1 cm时树冠体积

Ck、C1——点云体元边长为k、1 cm时点数量

测试结果见表3。表3第1列，点云体元表示1个点所占的立方体空间，数值越大，点云分辨率越低。分析表3可知，在设置相同参数情况下，随着点云分辨率降低，不同算法计算的树冠体积均呈下降趋势。其中，体元法受点云分辨率的影响波动较大，当点云体元边长为10 cm时，损失了原始树冠体积的51.016 6%；Graham算法与本文算法体积下降的幅度相较于去除点云的比例相对较小，在点云体元边长为10 cm，且抽稀后点云数量仅为原始点云样本的3.478 0%的情况下，损失了原始树冠体积的13.746 1%和11.804 6%。这说明本文算法在相同的迭代步长与分层间距下，计算结果受点云分辨率影响相对较小，高密度点云使用的相关参数对于低密度数据亦具有一定适用性，在一定程度上说明了本文算法的稳定性。

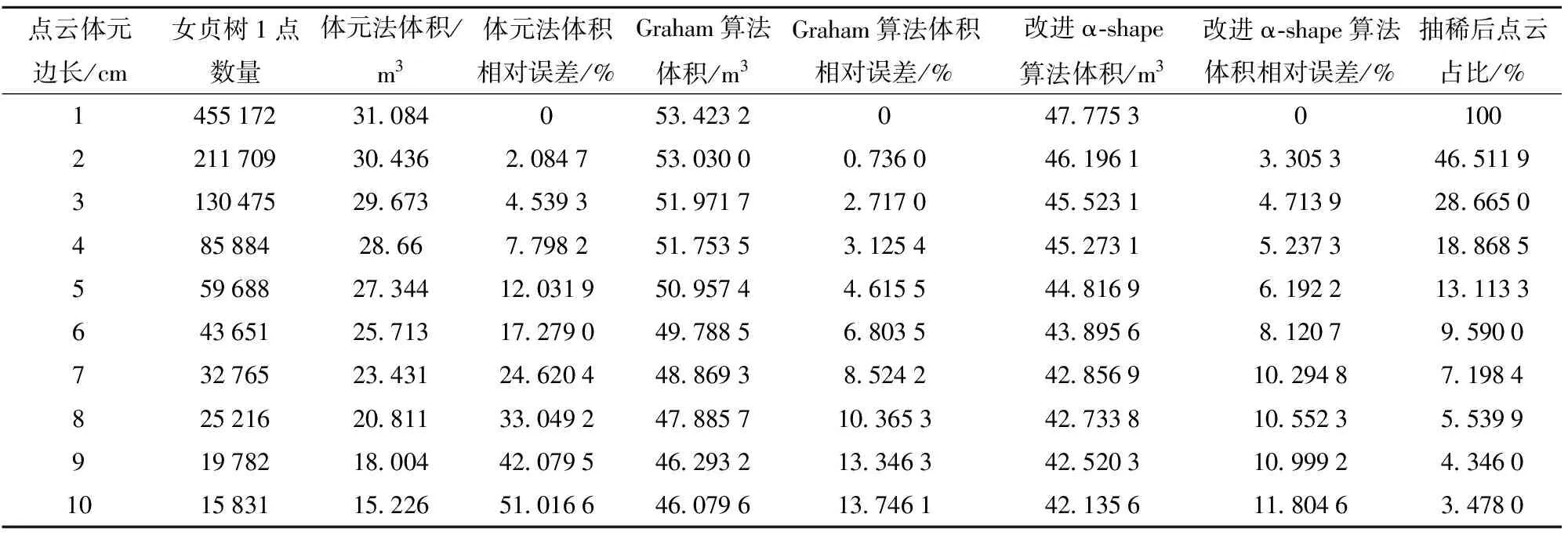
表3 抽稀与计算结果

4 结论

(1)树冠体积计算的准确性与树冠内部枝叶结构和点云密度均有关系。

(2)本文算法对不同树种树冠体积计算具有较好的适用性，无论对于高密度还是低密度树冠，采用改进α-shape算法的树冠体积计算结果具有良好的稳定性，在过滤样本为原始点云样本3.478 0%的情况下，仅损失了原始树冠体积的11.804 6%，而且相较于已有其他方法更为准确，既避免了Graham凸包算法的高估问题，相较于体元累加法也更利于树冠总体占用空间的计算。