基于WDPR-8支撑与弯刀尾支撑的风洞对比试验研究

潘家鑫，林麒，吴惠松，周凡桂，王晓光

(1.厦门大学 航空航天学院，厦门361102； 2.中国空气动力研究与发展中心，绵阳621000）

风洞试验是获取飞行器气动特性的重要途径。在风洞试验中，传统的做法多采用刚性的尾撑、腹撑或背撑的支撑方式来将模型固定在风洞试验段［1］。但这些传统支撑方式不仅会破坏模型的完整性，还会导致模型周围流场不同程度的失真，需要对风洞试验数据进行支架干扰修正。例如，传统的尾支撑多系悬臂梁结构，模型处于支撑末端，刚度比较弱，尤其当模型较大时，容易发生振动。文献［2］指出，尾支撑的缺点是对模型的外形要求严格，局限性大，仅适合于单发动机的飞机或导弹模型。文献［3］则认为尾支撑杆的干扰主要集中在模型后部，可以改变尾支撑杆截面尺寸和长度使之减小；而尾支撑架则影响全流场，所以必须用流场测量和数值计算的方法研究其影响。

相比于传统硬式支撑系统，绳牵引并联机器人(Wire-Driven Parallel Robot，WDPR）技术用于飞行器模型的支撑系统，具有工作空间大、刚度高、质量轻、惯性小、易重构等优点。国外对该技术在风洞试验中的应用也有诸多探索［4-5］。美国佐治亚理工学院搭建了一个8绳牵引的6自由度模型支撑机构，研究该支撑下钝体模型的流动控制，但其不是并联机器人系统［6-7］。德国杜伊斯堡-埃森大学针对船体模型的吹风试验，设计了结合线性驱动器与滑轨系统的8根绳索支撑方式［8］。法国国家宇航研究局(ONERA）研制了9根绳的绳牵引并联支撑系统，可对所支撑的模型实现6自由度运动控制，并在立式风洞中进行尾旋试验［9-11］。美国加州通用动力中心设计了一款6自由度的绳系支撑机构VSS(Vane Support System），依靠4根具有空气动力学外形的绳索进行支撑，外部环形框架旋转带动绳索来改变模型姿态［12］。但鲜有国外文献将绳牵引并联机构支撑与其他支撑所取得的风洞试验结果进行比较。

国内，厦门大学航空航天学院林麒团队设计搭建了8绳牵引的绳牵引并联机器人WDPR-8原理样机，对其参数测量、工作空间、支撑方案设计和气动参数解算等关键问题进行了研究，针对SDM标模在低速风洞中进行了一系列非定常试验及动导数试验，并与文献中的吹风试验结果和数值仿真结果进行了对比［13］。但是，文献中的模型及风洞试验条件都与该团队不同。

鉴于弯刀尾支撑在风洞试验中的成熟程度及其测试结果得到空气动力学界认可的事实，本文选择弯刀尾支撑为参考对象，以检验WDPR-8作为风洞试验模型支撑的可靠性、可信度和可行性。

本文参考文献［14］，选择中国自行设计的双发动机布局的类F-22标准动态试验模型，设计了满足工作空间及绳系布局刚度要求的WDPR-8支撑样机，以及适用于2种支撑机构的内置六分量杆式天平测力方案，并将整座WDPR-8支撑系统样机安装于低速风洞试验段中进行了吹风试验。以同一模型分别用WDPR-8支撑和传统弯刀尾支撑在相同来流条件下得到的试验结果进行对比分析，考察WDPR-8支撑应用于风洞试验的可行性及吹风试验结果的有效性。

1 试验设备及模型

1.1 风洞及传统弯刀尾支撑机构

本文试验是在中国航空工业集团有限公司空气动力研究院的FL-5风洞中进行的。该风洞是一座低速开口单回流风洞，试验段长1.95 m，入口直径为1.5 m，风洞湍流度为0.19%，最大风速可达53 m/s，风洞各技术指标符合国军标GJB 1061—91［15］规定。

图1为配有传统弯刀尾支撑机构的FL-5风洞。该传统弯刀硬式尾支撑，除了刚性支撑结构件外，主要由两大相互独立的攻角机构和侧滑角机构组成。

图1 FL-5风洞及弯刀尾支撑Fig.1 FL-5 wind tunnel and machete tail support

图1中，弯刀尾支撑的攻角机构由电机驱动，带动行星减速器、蜗轮蜗杆减速器等机械部件运动，从而实现模型攻角范围在-10°～50°之间的变化［15-16］。其侧滑角机构采用直径约1.4 m的高精度旋转工作台加装高精度减速器结构形式，可实现试验模型从-90°～90°范围内的侧滑角变化［16-17］。

1.2 试验模型

考虑到FL-5风洞大小及阻塞比要求，本文试验采用的模型机身长为622 mm，展长为500 mm，如图2所示。

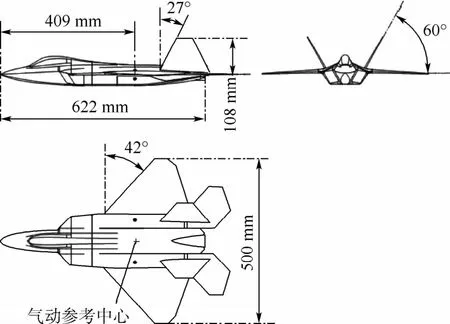
图2 试验模型的简要尺寸Fig.2 Brief sizes of test model

该模型气动布局为类F-22的、具备过失速机动能力的典型战斗机布局，采用翼身融合的双发机身、切尖菱形上单翼、V形双垂尾和全动平尾设计，具有较好的大攻角气动特性。根据文献［2］，该模型既非单发动机的飞机模型，也非导弹模型，不适用于传统弯刀尾支撑，因此本文选用其来进行WDPR-8支撑与传统弯刀尾支撑的比较研究。

鉴于该动态试验标模具有较为扁平的气动外形，将模型腹部设计为盖式结构，使六分量杆式天平方便嵌入模型腔内。机身尾部设计为筒状结构，方便将模型安装于传统弯刀尾支撑的支杆上。

1.3 WDPR-8支撑原理样机结构

图3为WDPR-8支撑原理样机的结构示意图。图中：机体坐标系Obxbybzb的原点Ob和飞机模型的质心重合；xb轴与飞机模型轴线重合且机头方向为正方向；zb轴垂直于xb轴，在飞机模型的纵向对称平面内指向下方；yb轴按照右手螺旋规则确定；样机框架尺寸依照风洞试验段尺寸设计，实现模型平稳吊装后，模型机身轴线与风洞试验段轴线基本重合。地轴坐标系Ogxgygzg位于机体坐标系下方的机架上；Ogxg轴沿风洞试验段纵轴，逆气流方向；Ogzg轴垂直于Ogxg轴，在风洞纵向对称面内指向下方；Ogyg轴按照右手螺旋规则确定。

牵引模型的8根凯夫拉绳采用菱形方式布置(见图3），该布置方式有针对性地保证了俯仰刚度。飞机模型通过绳索连接到伺服电机驱动的由滚珠丝杠和滑块等组成的单轴直线模组上。

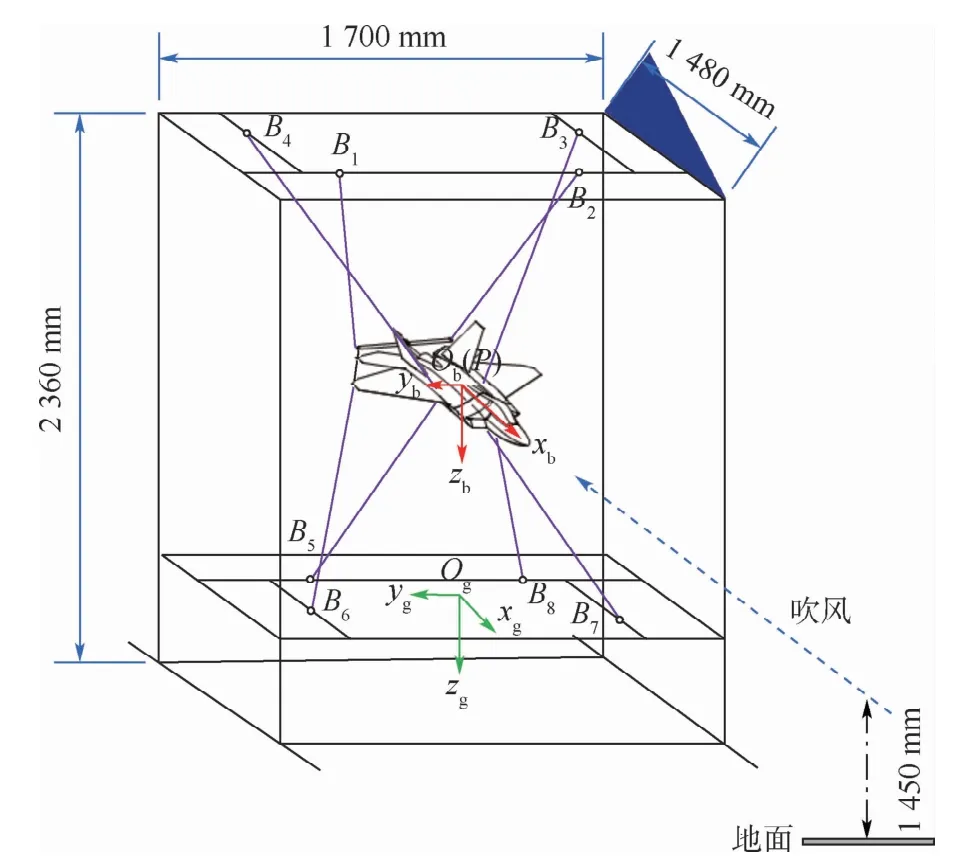
图3 WDPR-8支撑原理样机结构示意图Fig.3 Schematic diagram of structure of WDPR-8 support prototype

如图4所示，牵引绳与飞机模型上的点Pi(xbi，ybi，zbi）T(i=1，2，…，8）连接，通过固定在支架上的滑轮连接到驱动组件上。将滑轮简化视为铰点Bi(xgi，ygi，zgi）T(i=1，2，…，8）。

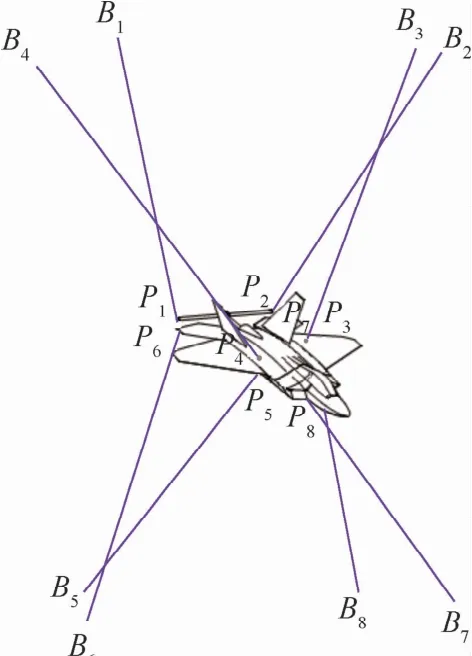
图4 WDPR-8铰接点的位置示意图Fig.4 Schematic diagram of joint points’location on WDPR-8

表1为Pi点和Bi点的具体坐标，其中Pi点是相对机体坐标系Obxbybzb下的坐标点，Bi点是相对地轴坐标系Ogxgygzg下的坐标点。

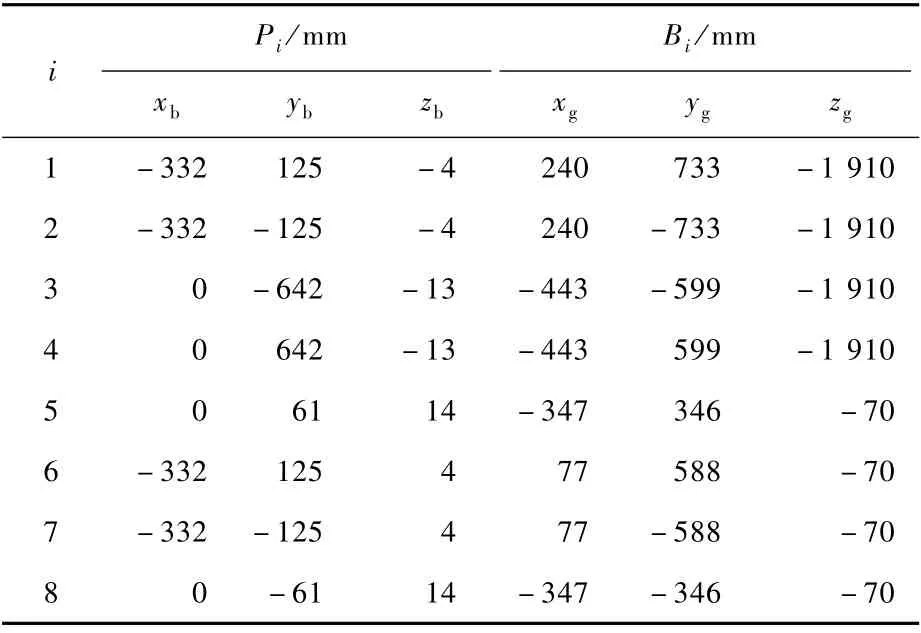
表1 WDPR-8支撑的结构参数Table 1 Structure parameter of WDPR-8 support

2 WDPR-8支撑系统

2.1 WDPR-8的运动学模型

WDPR-8支撑系统是通过控制绳长变化来实现对飞机模型位姿控制的。因此，需要建立机构的运动学模型来确定绳长变化与模型位姿之间的关系。

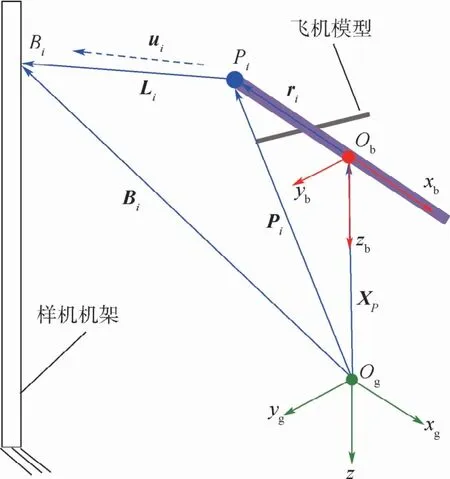
图5 WDPR-8支撑机构运动学关系示意图Fig.5 Schematic diagram of WDPR-8 support institutional kinematics relationship

式中：XP(Xp，Yp，Zp）T为机体坐标系Obxbybzb的原点Ob在地轴坐标系Ogxgygzg中的坐标；R为机体坐标系到地轴坐标系的旋转变换矩阵，具体表示为

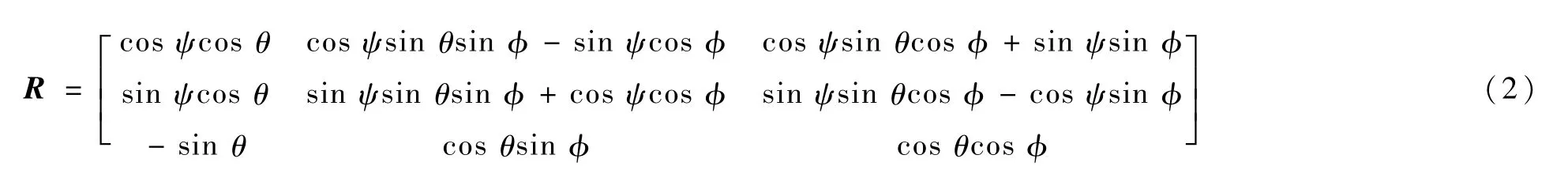
其中：φ、θ、ψ分别为飞机模型在地轴坐标系Ogxgygzg中绕Ogxg轴、Ogyg轴和Ogzg轴旋转的滚转角、俯仰角、偏转角。

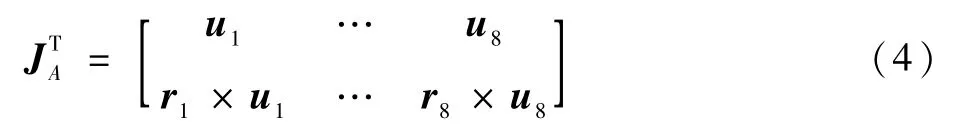
其中：ui为绳长方向矢量。

式(1）～式(4）建立了WDPR-8支撑的运动学模型，由此可确定绳长Li(i=1，2，…，8）与姿态角(φ，θ，ψ）T、飞机模型位置XP(Xp，Yp，Zp）T及其运动速度之间的对应关系。

2.2 气动力测量子系统

传统的空气动力天平主要有机械天平、应变天平、外式天平和张线天平。其中，应变天平和张线天平比较适合WDPR-8支撑系统的气动力测量。由于张线天平结构复杂、研制周期长、成本高等局限性，本文采用中国航空工业集团有限公司空气动力研究院提供的六分量杆式天平，型号为11-N6-18B。参照文献［13］，将天平安装于飞机模型腔内。天平与飞机模型固连成一个整体，在绳系并联机构传动组件驱动下进行6自由度运动。试验中，把天平测量得到的气动参数储存到数据采集系统中。

图6为模型基于WDPR-8支撑下的内部结构设计剖面图。图中：红色部件为六分量杆式天平，前端通过锥配合与模型固连，后端则采用锥套、连接尾杆(其伸出段直径为8 mm）及牵引绳的套筒配合固连。套筒上伸出机身的4根短杆及尾部的水平杆(直径为7 mm）分别与8根直径为1.2 mm的凯夫拉绳连接。4根短杆的伸出端面与模型面保持平齐。

绳索的另一端通过由电机驱动的单轴直线模组连接到试验样机的铝材机架上，从而搭建成绳系并联支撑系统的机械主体框架。为实现模型的气动中心尽可能接近重心，将可拔插的模型头部掏空使重心后移，水平杆使用空心不锈钢杆件，既保证刚度又减轻模型整体质量。

图7为模型安装于传统弯刀尾支撑上的结构设计剖面图。天平前端也是通过前锥套与模型固连。蓝色杆件为尾支连接件(伸出段直径为20 mm），其前端通过锥配合与天平尾端固连，另一端与尾撑支杆锥配合，并且表面左旋螺纹可以通过尾撑支杆的螺帽将连接件沿轴向拉紧。当模型采用弯刀尾支撑时，原安装在WDPR-8支撑上时伸出短杆的4个孔用0.02 mm厚的铜箔封住，防止气流窜入模型腔内。

以上天平安装方案可以较大程度地保证支撑对比试验条件的一致性，较为客观地验证了WDPR-8支撑系统的可行性。

本文所用的FL-5风洞弯刀尾支撑，其尾支撑杆长达1.5 m，具有一定锥度，截面直径从连接模型末端处的35 mm过渡到弯刀支点处的70 mm。比较图6和图7，显见WDPR-8支撑的尾杆截面和长度都比弯刀尾支撑在尺寸上小很多，而且没有弯刀尾支撑粗大的后支架。根据文献［3］可知，WDPR-8支撑的尾杆干扰比较小，也没有弯刀尾支撑架对全流场的影响。

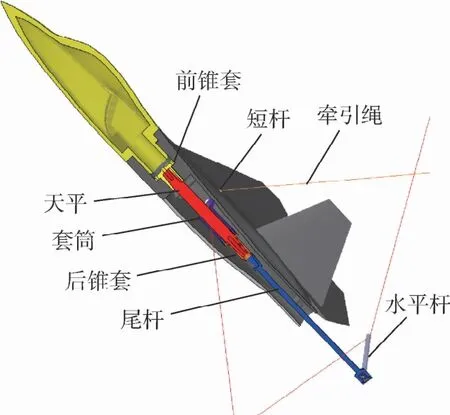
图6 应用于WDPR-8支撑下的模型结构剖面图Fig.6 Model structure profile applied to WDPR-8 support

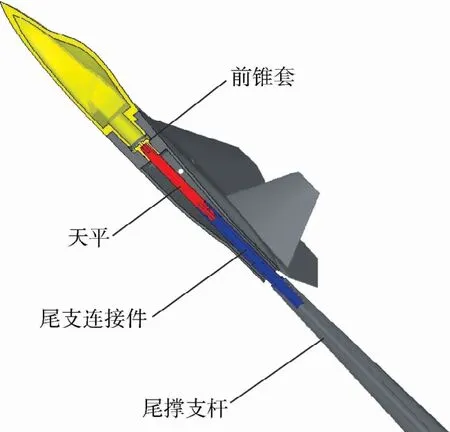
图7 应用于弯刀尾支撑下的模型结构剖面图Fig.7 Model structure profile applied to mathetes tail support

2.3 模型位姿单目视觉测量子系统

由于模型用绳牵引悬挂在空中，本文采用单目视觉子系统(Monocular Vision Subsystem，MVS）测量模型的位姿［18］，该系统主要由CMOS相机、红外光源、红外滤镜、1394采集卡、标定板、SDM标模上的6个荧光特征点及机器视觉图像处理软件等构成。

MVS子系统建立时，在测量模型位姿前，需要采用标定板确定相机的基准坐标系，根据支撑机架尺寸使坐标系原点Ob位于风洞试验段的中心位置。吹风试验前，先对模型的初始位姿进行标定。通常使模型的位姿归零，即机体坐标系的坐标原点Ob与相机基准坐标系的坐标原点重合，模型的3个姿态角均为零。模型运动过程中，通过CMOS相机获取到表征飞机模型位姿的6个荧光特征点，经过图像处理及位姿求解获得飞机模型相对相机基准坐标系的位姿，继而完成模型位姿的采集。

文献［19］给出了单目视觉测量子系统的测量精度。该子系统采用北京航空精密机械研究所出品的高精度三轴转台(型号：SGT320E，各轴精度：±5″）进行了标定。3个姿态角的标准差最大为0.010 6，最小为0.002 84；对各姿态角的静态测量误差为：俯仰角和滚转角的测量误差均小于0.1°，相对误差均小于0.7%；侧滑角的测量误差小于0.15°，最大相对误差为0.9%。

2.4 WDPR-8运动控制子系统

软件系统部分在上位机完成执行工作。运动控制子系统的硬件核心采用PMAC可编程多轴运动控制器。当要实现指定位姿时，上位机提交控制指令给运动控制程序，经解算后传输给PMAC运动控制器。PMAC运动控制器将指令进一步处理后发送给伺服驱动器，伺服驱动器将接收的运动信号分解处理后发送给8个伺服电机。伺服电机根据收到的指令驱动与其相连的滚珠丝杆上的滑块滑动，带动连接飞机模型的绳索收放，改变绳长，最终完成对模型的位姿变化控制。

3 试验数据处理方法

本文的纵向测力试验采用攻角阶梯变化法，该方法预先给定模型攻角变化阶梯，当模型姿态达到预定的攻角后作短暂停留，待所测各参数稳定后进行数据采集，当数据采集完毕后进入下一个预定的攻角阶梯，直到测完全部预定的攻角为止［20］。在横向测力试验中，通过预偏侧滑角测出给定攻角下模型在不同侧滑角时的空气动力分量［21］。本文基于WDPR-8支撑系统进行了单自由度俯仰振荡试验，给定模型振荡规律和采集时间，从而得到模型的非定常气动特性。

由于采用2种不同形式的支撑方式，试验数据处理时对支架干扰进行的修正有所不同。FL-5风洞的测量系统具有完备的吹风试验数据处理程序，本文采用该程序对2种支撑获得的测量数据进行处理。

传统弯刀尾支撑对测力试验数据处理时进行了以下修正：①通过吹风时天平数据减无风时天平数据来扣除模型的惯性量；②修正了模型尾部由于弯刀尾支撑系统的干扰影响，修正方法一般采用专门的支架干扰试验来获取干扰量；③扣除了风洞试验段平均气流偏角的影响；④修正了天平因承受气动力和力矩作用产生的弹性角对模型姿态角的影响；⑤将绕天平校心测量的力矩修正到绕模型重心的气动力矩。详细的修正流程请参考文献［22］。

WDPR-8支撑系统与弯刀尾支撑相比，由于没有尾支架，且尾支杆细小很多，未进行尾支架干扰修正。

在FL-5风洞的试验数据处理程序中，设置有“支架干扰”的选项按钮。处理弯刀尾支撑数据时，勾选该选项；处理WDPR-8支撑数据时，未勾选。事实上，许多文献也基于张线支撑在模型后端保留或移除支杆来扣除支架干扰量。

4 试验结果

本文主要对WDPR-8试验的结果进行验证性研究。表2为风洞吹风试验工况。试验内容包括：有效性验证试验(包括以WDPR-8为模型支撑的7次重复性试验、相同条件下与弯刀尾支撑的对比试验）、基本纵横向试验、单自由度俯仰振荡试验等。静态试验内容均在来流30 m/s下完成。

表2 风洞试验工况Table 2 State and condition of wind tunnel test

图8为模型加装WDPR-8支撑系统的试验现场照片。由于牵引绳很细(直径只有1.2 mm），不易识别，故用红色长箭头描绘。图中的铝合金框架为WDPR-8支撑系统样机支架，为增强系统刚度，采用6090铝型材搭建。除1.2 mm凯夫拉绳以外的所有支架及硬件系统都在风洞试验段以外。从牵引绳的分布及其所占空间大小来看，WDPR-8支撑系统相比于传统弯刀尾支撑对试验段流动的干扰较小。

图8 模型基于WDPR-8支撑下的试验照片Fig.8 Test photos of model supported by WDPR-8

4.1 重复性试验

本文在风速30 m/s下，用2种支撑进行了重复性试验。图9为基于WDPR-8支撑系统，侧滑角和滚转角均为0°时得到的升力特性曲线7次重复性试验结果。图中：CL为升力系数，α为攻角。

根据文献［2］中关于低速风洞试验重复性试验精度的标准，表3给出了2种支撑各自的7次重复性试验均方差分析数据。

均方差是试验值x与平均值μ偏差的平方和与观测次数N比值的平方根，即

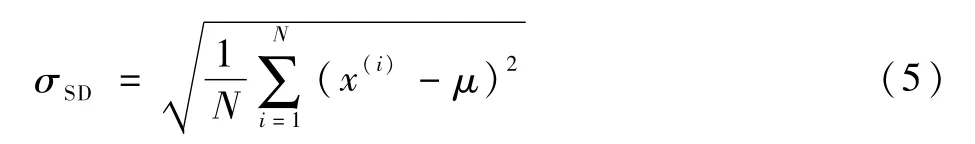
式中：x为WDPR-8支撑得到的试验结果；μ为多次试验结果的平均值。

比较分析所得的表3数据，虽然WDPR-8支撑与弯刀尾支撑的重复性试验的均方差结果不尽相同，但也都在一个数量级上，差别不大。在俯仰力矩方面，悬臂梁结构类型的弯刀尾支撑杆相比于WDPR-8支撑，最大均方差还稍大一些。

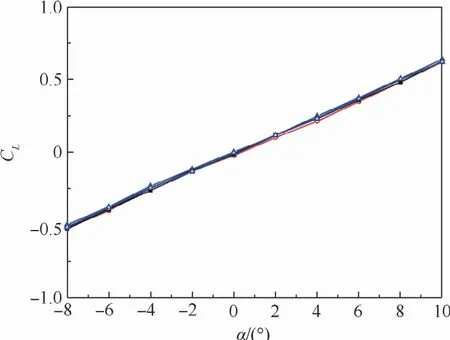
图9 基于WDPR-8支撑试验结果精度验证Fig.9 Accuracy verification based on WDPR-8 support test results

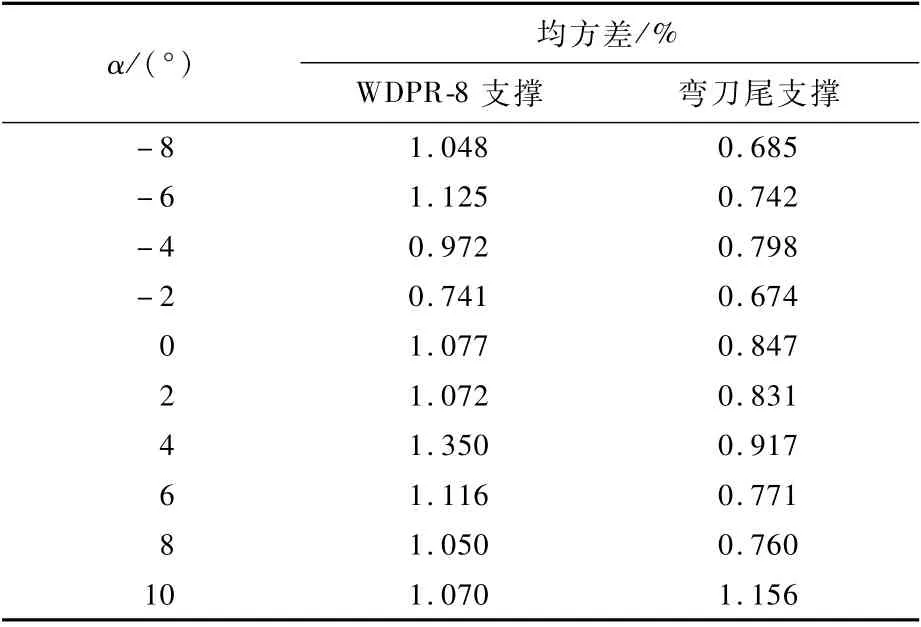
表3 重复性试验的均方差结果Table 3 Mean variance results of r epeatability tests

试验所用的弯刀尾支撑是很成熟的试验装置，而本文的WDPR-8支撑还是比较初步的原理试验样机，限于财力物力，制作得比较粗糙，能达到这样的精度应是可取的。今后如果有条件，采用性能更好的相机，质量更高的零部件，样机建造得更精密些时，相信可以大幅提高重复性精度。

4.2 纵向试验

图10～图13为分别采用WDPR-8支撑和弯刀尾支撑作为模型支撑，在相同来流风速V0下进行纵向试验得到的升力系数CL、阻力系数CD和俯仰力矩系数CM的曲线。为方便比较，在每幅图中同时给出基于2种支撑的试验数据。

如图10所示，2种支撑得到的升力系数曲线都符合小展弦比飞机模型的升力系数斜率在非线性段随攻角α而改变的规律，最大升力系数CLmax均出现在攻角38°左右。

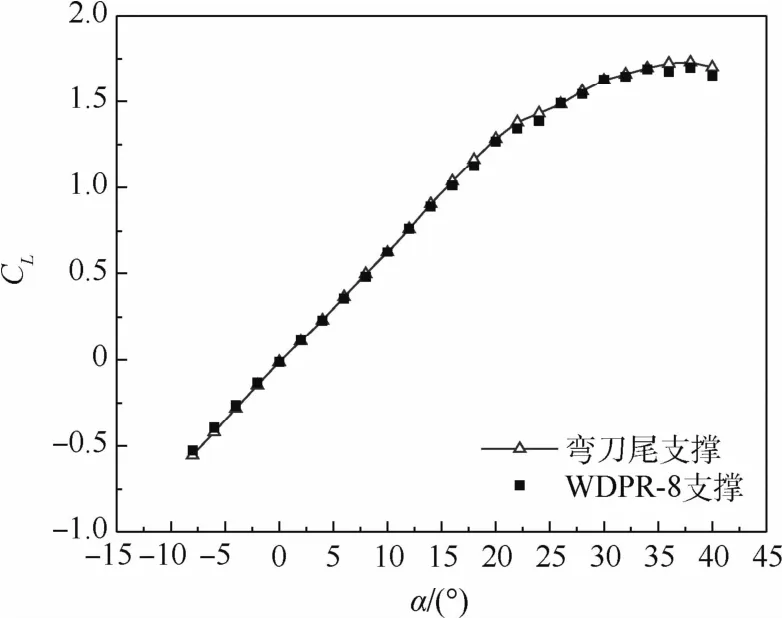
图10 升力特性曲线对比(V0=30 m/s）Fig.10 Comparison of lift characteristic curves atV0=30 m/s

由图11中的极曲线可以看出，同一模型在WDPR-8支撑和传统弯刀尾支撑下的零升阻力系数CD0、最小阻力系数CDmin相差较小，最大升阻比点也几乎在同一位置。

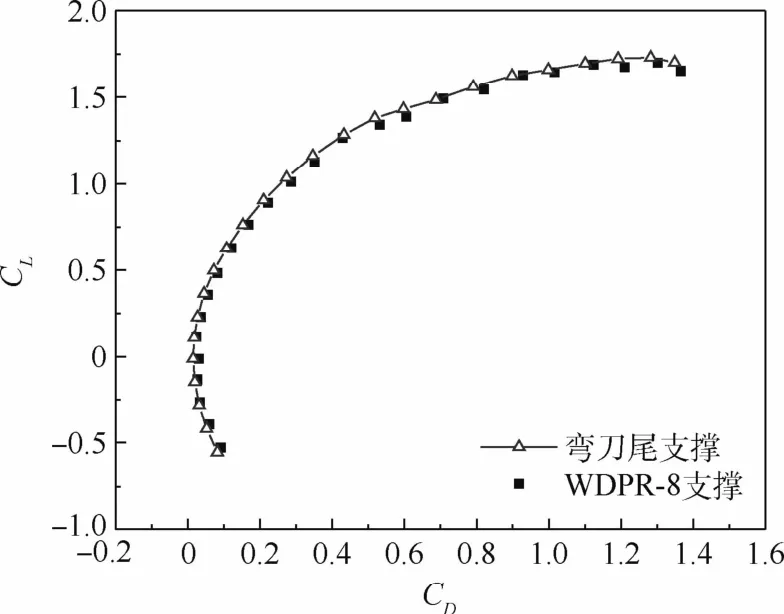
图11 极曲线对比(V0=30 m/s）Fig.11 Comparison of polar curves at V0=30 m/s

从图12可以看出，由于F-22具有V型斜尾翼的气动布局特点，在攻角12°～20°范围内成非线性俯仰力矩特性。攻角大于20°后，2种支撑的数据才出现些许的差别。这是因为本文弯刀尾支撑采用的是直尾支撑杆，且较细，在小攻角范围内的风洞试验中对流场的干扰较小，2种支撑在小攻角范围的试验结果比较吻合。由于WDPR-8支撑所得结果的数据处理没有进行支架干扰修正，也可说明WDPR-8支撑在小攻角情况下对于低速流场影响甚微，在大攻角下影响也不大。

风洞试验结果验证了文献［3］的论述，即WDPR-8支撑的尾支杆较细及无尾支架的支撑形式对流场干扰较小。

取试验值x为WDPR-8支撑得到的试验结果，取弯刀尾支撑得到的试验结果y为对照参考值，则均方根误差是试验值x与参考值y偏差的平方和与观测次数N比值的平方根，即

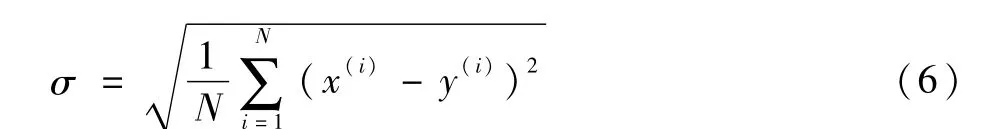
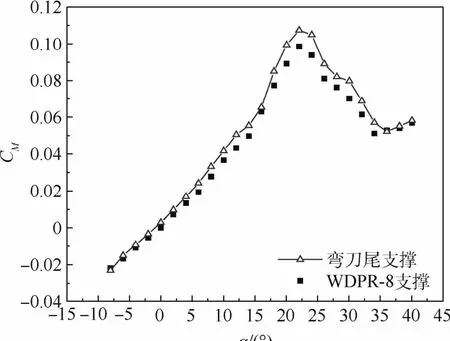
图12 俯仰力矩系数曲线对比(V0=30 m/s）Fig.12 Comparison of pitching moment coefficientcurves at V0=30 m/s

图13为WDPR-8支撑相对于弯刀尾支撑试验结果的气动系数均方根误差σ。其中，取观测次数N=3，升力系数最大均方根误差为3.551%，阻力系数最大均方根误差为3.031%，俯仰力矩系数最大均方根误差为1.088%，三者都不大。分析结果验证了WDPR-8支撑系统与测力方案的有效性。

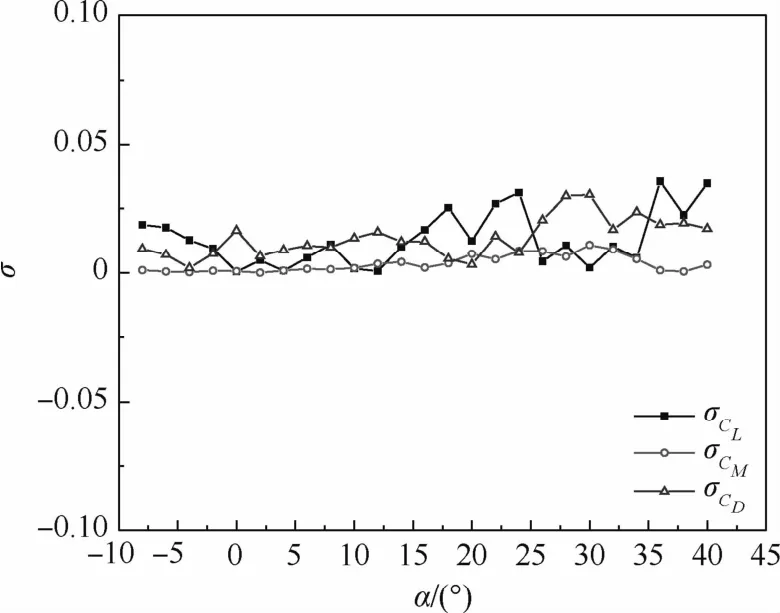
图13 两种支撑结果气动系数的均方根误差曲线(V0=30 m/s）Fig.13 Mean square error curves of aerodynamic coefficients of two kinds of support results at V0=30 m/s

图14给出了2种支撑的纵向静稳定度情况。纵向静稳定度指的是单位升力系数变化时俯仰力矩系数的变化量，即

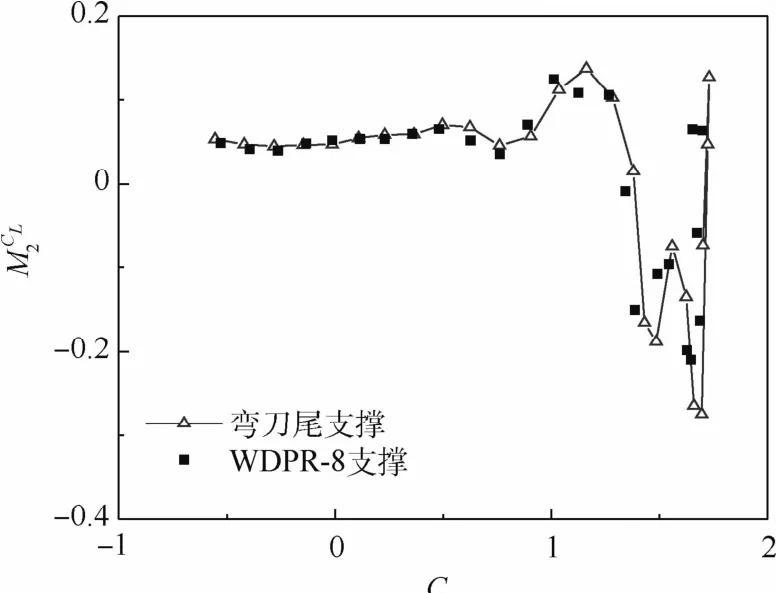
图14 纵向静稳定度对比(V0=30 m/s）Fig.14 Comparison of longitudinal static stability at V0=30 m/s

式中：MCL2为纵向稳定度(俯仰稳定度）；ΔCM为俯仰力矩系数的变化量；ΔCL为升力系数的变化量。

由图14可见，随着升力系数CL增大到一定值后，2种支撑的纵向静稳定度都发生规律相同的较大变化。

从以上纵向试验结果可以看出，WDPR-8支撑的数据处理虽未进行尾支架干扰修正，但与很成熟的弯刀尾支撑结果相比，相当一致。这表明WDPR-8支撑作为模型支撑是可行的。

4.3 横向试验

图15为采用2种支撑在改变侧滑角时得到的横向试验结果。

由表4可以看出，2种支撑结果的侧向力系数在小攻角范围内相差较小，且最大均方根误差随侧滑角增大而增大。

表4 两种支撑所得侧向力系数的最大均方根误差Table 4 Maximum mean square error of lateral force coefficient obtained from two supports

在图15(b）中，2种支撑所得结果的规律基本相同，只有β=-15°且攻角较大时的情况差别较大。在中小攻角范围内，2种支撑所得侧向力系数对侧滑角的导数CβY始终为负值。在较大侧滑角且攻角16°～34°的范围内，2种支撑都体现侧向力有先下滑后上升的规律，原因可能是模型抬头过程中，主翼对斜尾翼有一段遮挡过程，即模型总迎风面积有一个先减小后增大的过程。

4.4 单自由度俯仰振荡试验

WDPR支撑在不调整支撑机构的情况下可以继续完成一系列非定常试验。下面给出模型做单自由度俯仰振荡的试验结果。模型做简谐运动的规律为

式中：f为振荡频率；A为振荡幅值；α0为振荡平衡角。

定义模型做俯仰振荡运动的减缩频率κ为

式中：ω=2πf为振荡圆频率；试验模型平均气动弦长cA为0.252 2 m。

图16(a）为振荡幅值为5°，风速V0=20 m/s时，减缩频率κ分别为0.026 9和0.053 8(振荡频率分别为0.34 Hz和0.68 Hz）得到的单自由度俯仰振荡结果。

图16(a）中的升力系数CL曲线呈现出明显的迟滞效应现象，整条曲线为非定常迟滞环串接曲线。这种典型的非定常气动现象是因为当模型上仰时，涡破裂的推迟导致产生增大的气动力载荷量；而在下俯过程中，则是由机翼前缘涡的再附推迟引起气动力载荷量减小，因此在一个局部振荡运动过程中升力系数CL出现迟滞环。从图中也可以看出，升力系数的动态测试结果曲线与静态试验曲线走势的一致性较好，而且各平衡角阶梯下的升力系数CL迟滞环首尾相连。

图16(b）为图16(a）中振荡平衡角α0=0°时的非定常迟滞环放大图。可以看出非定常迟滞环面积随频率增大而增大的现象，说明本文基于WDPR-8支撑系统得到的单自由度俯仰振荡试验结果是有效的。

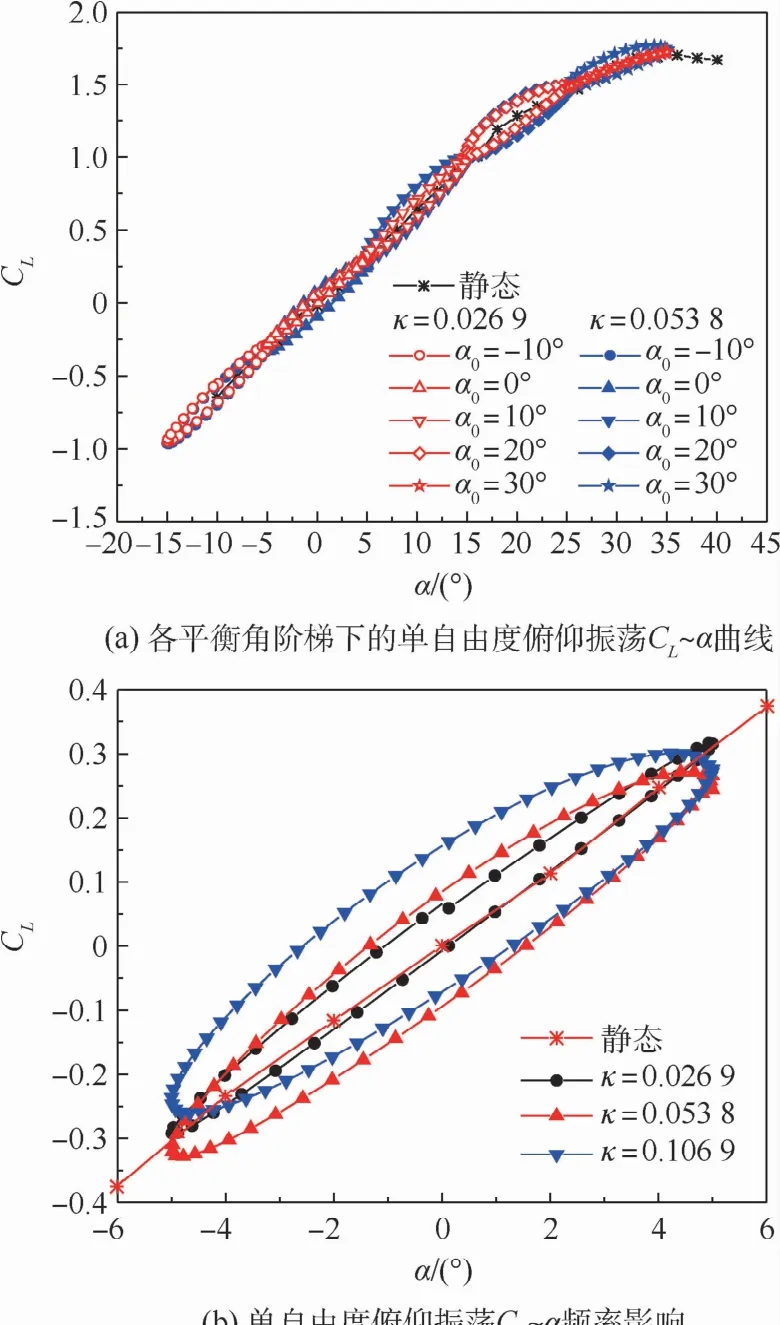
图16 单自由度俯仰振荡升力系数曲线Fig.16 Single-degree-of-freedom pitching oscillation lift coefficient curves

5 结 论

本文采用对比分析法，在低速风洞中完成了有效性验证试验、基本纵横向试验、单自由度俯仰振荡试验等，探讨了相应的试验数据处理方法；在对弯刀尾支撑进行支架干扰修正，而WDPR-8支撑未进行支架干扰修正的情况下，所获得的结果以相同试验条件下弯刀尾支撑所得的试验结果为参考值进行对比，验证了WDPR-8支撑的可行性和有效性。

研究得到以下结论：

1）将六分量杆式天平内嵌于较扁平飞机模型进行气动力参数测量的设计方案是可行有效的。

2）以WDPR-8支撑与传统弯刀尾支撑作为模型支撑进行静态测力试验，2种支撑的试验结果在趋势与数据量级上均表现出合理的一致性。

3）在横向测力试验中，WDPR-8支撑与传统弯刀尾支撑所得试验结果规律一致。

4）在WDPR-8支撑中完成的单自由度俯仰振荡试验结果符合物理规律，也符合所用模型的气动特性，表明其作为动态试验支撑的可行有效性。

5）不必更换或改变支撑机构，WDPR-8支撑就可无障碍地方便实现由基本纵横向测力试验到非定常试验的切换，且结果可信有效。

研究结果显示了WDPR-8支撑的优越性，以一套WDPR-8支撑不仅可以进行静态试验，也可以进行多种动态试验。虽然WDPR-8支撑的安装比弯刀尾支撑工作量稍微大一些，但免去了为进行不同的动态试验更换支撑(甚至需要更换风洞）和模型多次安装的繁复工作，提高了风洞使用的利用率。因此，WDPR-8支撑在风洞试验方面具有实际应用前景。

致谢 感谢中国航空工业集团有限公司空气动力研究院哈尔滨研究所的大力支持；吴太欢、高忠信、柳汀等同学参与了本文研究，特别是参与了风洞试验，在此一并致以衷心的感谢！