北斗三号系统广域差分服务精度评估
2021-06-09田秋凝曹月玲胡小工唐成盼郭睿杨宇飞
田秋凝,曹月玲,胡小工,唐成盼,郭睿,杨宇飞
(1.中国科学院上海天文台,上海200030; 2.中国科学院大学,北京100049;3.中国人民解放军32021部队,北京100094; 4.北京卫星导航中心,北京100094)
随着全球导航卫星系统(GNSS)的广泛应用,为满足导航用户更高精度的服务需求,很多国家和地区建立了星基增强系统,如美国的WAAS系统、欧洲的EGNOS系统、日本的MASA系统以及印度的GAGAN系统等[1-4]。通过在服务区域内均匀布设监测站,解算卫星的轨道与钟差误差改正信息、格网电离层延迟改正信息和差分完好性信息,再通过GEO卫星播发给用户使用,以满足用户的增强服务需求[5-6]。其中,WAAS系统用户在服务区域内大部分地区可以获得水平方向优于1.0 m、高 程 方 向 优 于1.5 m的 定 位 精 度[7];EGNOS系统为欧洲地区的用户提供1.5 m以内的定位精度[8-9];GAGAN系统用户的定位精度达到了水平和高程方向误差均小于7.6 m的水平[10-11]。
北斗二号系统(BDS-2)在初始设计中同时考虑了基本导航服务和增强服务,但增强服务不是提供满足国际民航(ICAO)标准规范的星基增强(SBAS)服务,而是采用的广域差分服务方式,称为北斗二号协议广域差分服务。通过GEO卫星B1I/B2I/B3I频点发播D2电文,提供等效钟差改正数和格网电离层延迟改正及其相应的完好性信息,实现对中国及周边地区的广域差分增强。
北斗二号协议广域差分服务的信息类别及更新周期如表1所示[12]。其中,等效钟差改正数表示的是卫星广播星历中轨道误差与钟差误差的综合改正误差[13-14]。不同于WAAS等星基增强系统提供5°×5°格网模型,为了提高中国中低纬度地区的电离层格网改正精度,北斗二号协议广域差分系统提供5°×2.5°格网模型,在大部分服务区内电离层延迟修正精度可优于0.5 m[15]。
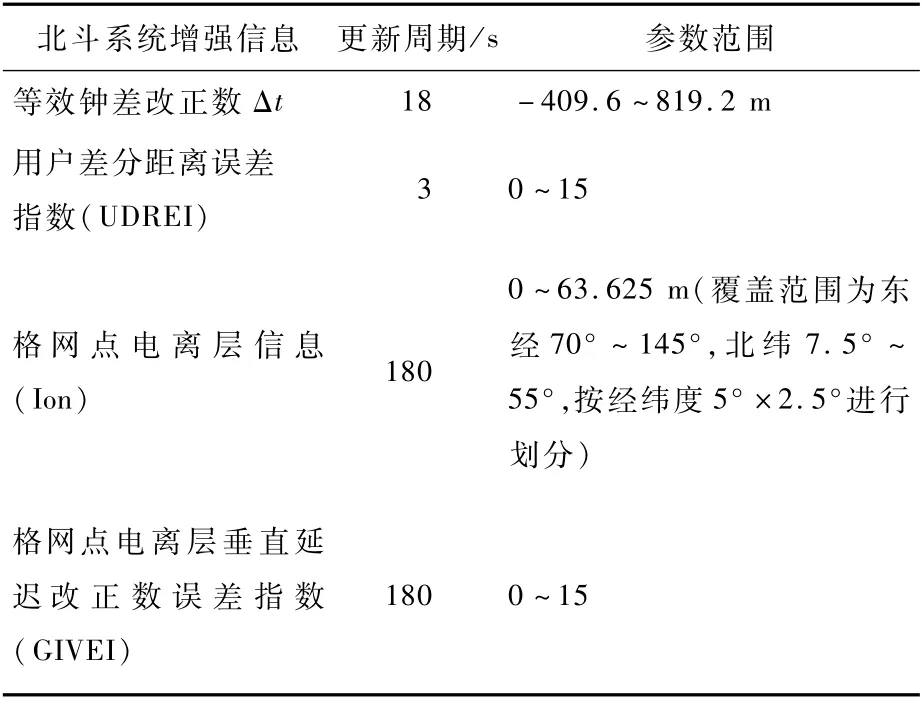
表1 北斗二号协议广域差分服务的信息类别及更新周期[12]Table 1 Information types and update period of the wide area differentiated services of BDS-2 protocol[12]
随着北斗三号全球导航系统建设(BDS-3),BDS-3利用B1C与B2a信号播发满足ICAO标准协议要求的星基增强服务。但为了保证北斗二号协议广域差分服务的平稳过渡,BDS-3仍然在GEO卫星的B1I和B3I信号上通过D2电文继续播发北斗二号协议广域差分增强信息。因此,BDS-2和BDS-3均提供北斗二号协议广域差分服务,显著增强了用户的可用卫星数,于此同时,由于BDS-3采用了星间链路测量体制和更稳定的星载原子钟,可以提供更高精度的广播星历参数,本文对不同基本导航服务精度下的广域差分改正精度也进行了对比分析。目前,北斗二号协议广域差分服务增强的卫星列表如表2所示,包括16颗BDS-2卫星和26颗BDS-3卫星。

表2 北斗二号协议广域差分服务所增强的卫星信息Table 2 Information of satellites enhanced by the wide area differential services of BDS-2 protocol
随着BDS-3星座的完善,本文利用中国境内均匀分布的监测站实测数据对BDS-2/BDS-3联合条件下的广域差分服务性能进行了评估,介绍了北斗广域差分改正数的解算方法,分析了不同差分改正参数的修正精度,以及BDS-3系统加入对北斗广域差分服务的增强效果。
1 广域差分改正数解算方法
北斗系统通过GEO卫星B1I和B3I频点播发等效钟差改正数、格网点电离层垂直延迟改正数和相应的广域差分完好性信息。其中,等效钟差参数用于广播电文中轨道和钟差预报误差的修正,格网点电离层垂直延迟参数为单频用户提供服务区内5°×2.5°的格网点电离层延迟改正数,实现对单、双频用户的广域差分服务。
1.1 等效钟差改正数解算
基于伪距观测量,可以得到常见的伪距残差观测方程为
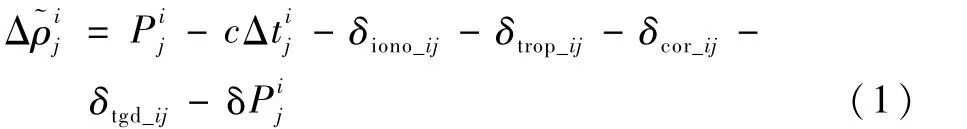
电离层延迟误差采用双频消电离层组合进行消除,而对流层、相对论、天线相位中心等一系列系统误差则通过相应模型进行改正[16]。为了降低伪距多路径误差对参数解算精度的影响,采用CNMC(Code Noise and Multipath Correction)相位平滑伪距方法对伪距观测量进行平滑[17]。这样,在伪距残差观测方程中只剩余了轨道误差、卫星钟差和接收机钟差3项不能有效消除,在北斗广域差分服务中将卫星轨道误差与卫星钟差综合为一体,以等效钟差改正数pcori的形式发播,表示为

式中:δorb_i为卫星i的轨道径向投影误差;δsatclk_i为卫星i钟差误差。
因而,式(1)伪距残差观测方程可以进一步表示为
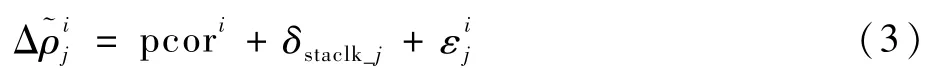
式中:pcori为卫星i的等效钟差改正数;δstaclk_j为监测站j的站钟差为伪距观测噪声,包含多路径噪声和对流层模型修正残差等。
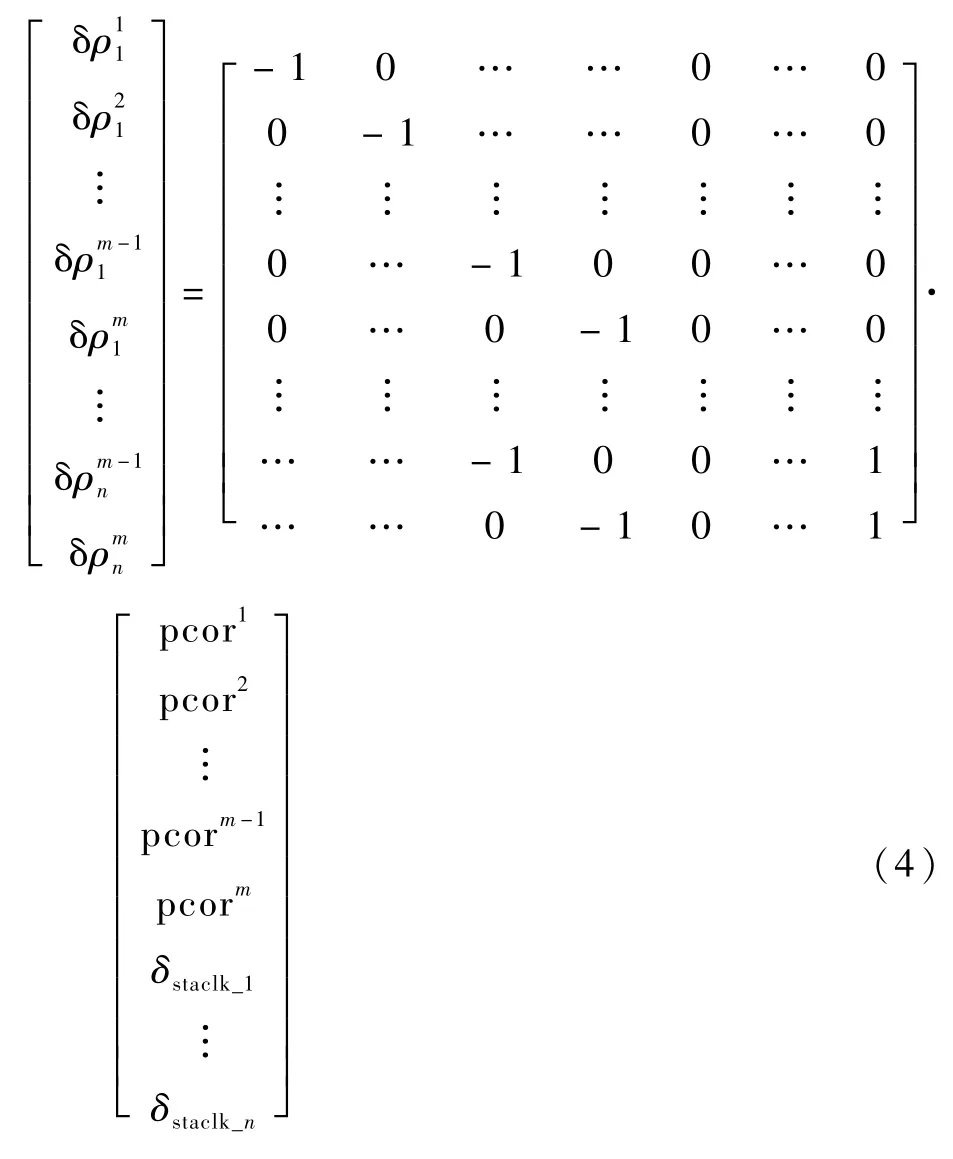
基于服务区域均匀分布的监测站观测数据,构建观测方程组,采用最小二乘的方法解算境内卫星的等效钟差参数。根据式(3)可以了解到方程组中除等效钟差参数外,还需解算接收机钟差,为避免方程组解算秩亏,固定一个监测站站钟差,如式(4)所示:
1.2 格网点电离层垂直延迟改正数解算
与基本导航服务所提供的Klobuchar 8参数模型不同,广域差分服务将服务区域划分为5°×2.5°的格网,提供每个格网点电离层垂直延迟参数,用户可直接通过格网点插值解算穿刺点处的电离层误差。由此,为解算服务区内格网点处的电离层延迟值,系统基于服务区内均匀分布的监测站实时观测数据,采用双频组合解算电离层误差,从而根据穿刺点处的电离层延迟值拟合得到服务区内格网点的电离层垂直延迟参数。
利用双频组合解算高精度的穿刺点处电离层延迟值,即
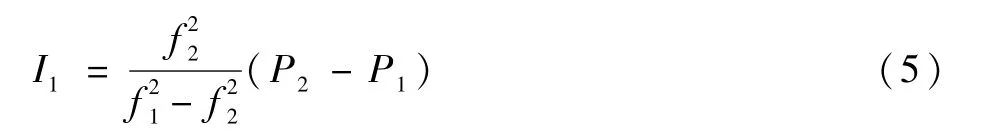
式中:I1为B1I频点的电离层延迟量;f1和f2分别为B1I和B3I频点频率;P1和P2分别为B1I和B3I频点经各项修正后的伪距观测值。
广域差分服务区域内电离层格网设为5°×2.5°,则根据穿刺点与格网点的距离进行筛选,获取格网点周围4个象限内穿刺点的电离层延迟,从而拟合格网点处电离层垂直延迟改正数,即
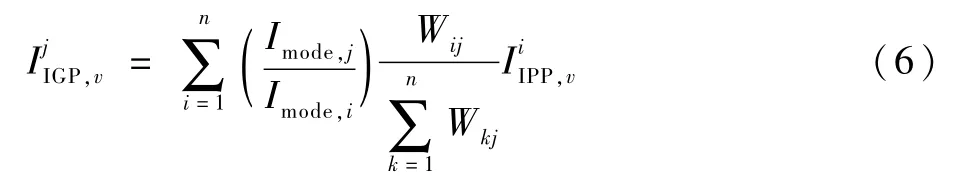
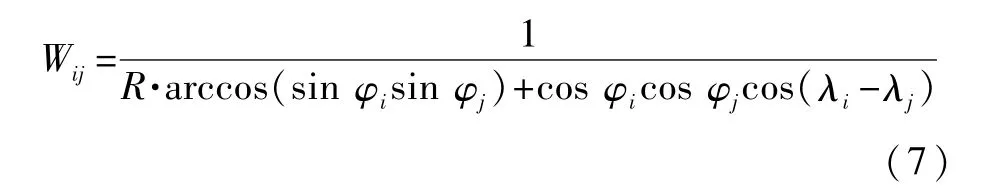
式中:R为地球半径;(φi,λi)为穿刺点i经纬度;(φj,λj)为格网点j经纬度。
由此,可以解算出服务区域内高精度的格网点电离层参数。
2 广域差分改正数特性分析
2.1 等效钟差改正数特征
根据等效钟差改正数的解算方法可知,等效钟差改正信息中除卫星轨道预报误差在视向上投影和卫星钟差预报误差外,还可能包含系统监测站的测量误差。为了分析等效钟差改正数变化特性,本文对2019年10月26日至10月28日连续3天3种不同类型轨道卫星的等效钟差改正数进行分析,如图1所示。图1(a)、(b)、(c)分别为3颗GEO卫星(C01、C04和C05)、3颗IGSO卫星(C06、C07和C39)和3颗MEO卫星(C25、C20和C36)的等效钟差改正数时间序列。
从图1可以看出,GEO卫星的等效钟差改正数存在明显的日周期波动,IGSO卫星与MEO卫星的等效钟差改正数在出入境时存在较大变化。
为了进一步分析等效钟差改正数与广播星历中轨道预报误差和钟差预报误差的关系,本文以地面运控系统事后精密轨道产品为参考,利用2019年10月26日北斗卫星导航电文数据来评估广播星历中轨道预报误差。事后精密轨道产品是利用星地链路和星间链路联合处理结果,轨道径向精度优于10 cm[18]。广播星历中轨道预报误差可表示为
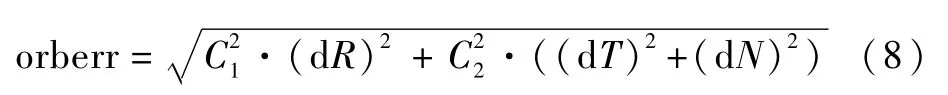
式中:orberr为轨道预报误差;d R、d T和d N分别为广播星历与精密星历相比在轨道径向、切向和法向的误差;C1和C2为常量,具体如表3所示。
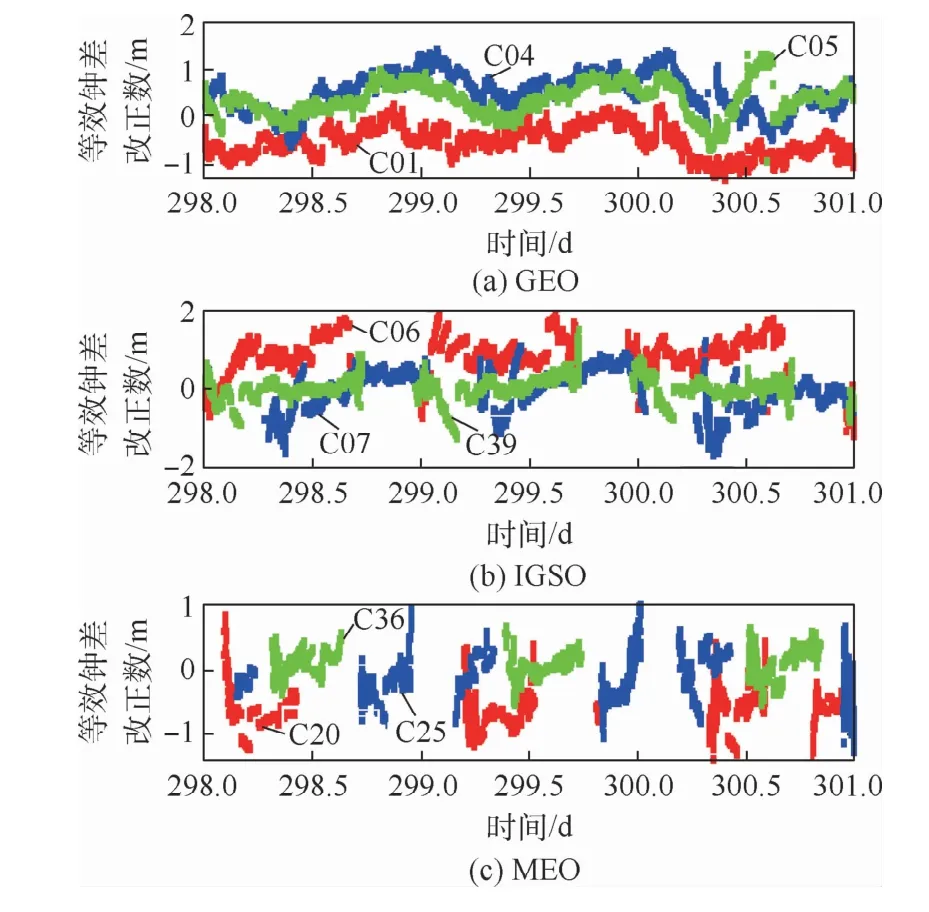
图1 2019年等效钟差改正数的时间序列图Fig.1 Time series of equivalent clock correction in 2019
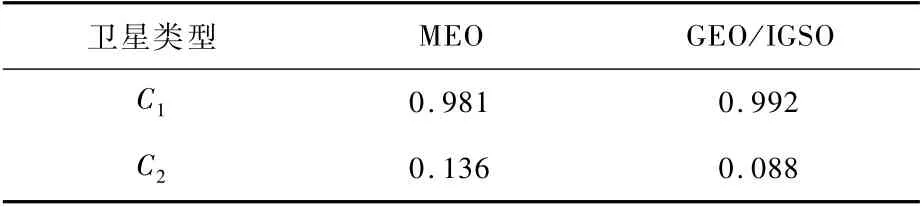
表3 C1和C2常量取值Table 3 Constant values of C1 and C2
利用北斗双向时间同步观测数据解算卫星钟差,与广播电文钟差预报值进行作差比较,计算广播电文钟差预报误差。文献[19]中给出了精密钟差的计算方法,利用双向时间同步观测计算的精密钟差精度优于0.5 ns。广播钟差预报误差的计算方法为
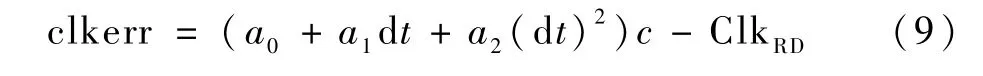
式中:clkerr为钟差预报误差;a0、a1和a2分别为广播电文中钟差、钟偏和钟漂;d t为计算时刻与电文参考时刻的时间差;ClkRD为精密钟差。
为了分析广播星历轨道预报误差、广播钟差预报误差和等效钟差改正数三者之间的关系,图2给出了三者随时间变化的序列图,选取BDS-3的C20卫星为代表进行说明。可以看出,受导航电文的更新周期影响,卫星钟差参数误差存在每小时阶跃现象,导致等效钟差改正数也跟随电文更新发生阶跃。另外,可以看到广播钟差预报误差与等效钟差改正数间具有明显一致的变化趋势,但是两者之间存在一个近似常量的偏差。通过分析发现,这是由于在利用精密钟差计算广播星历钟差预报误差时,存在双向时间同步设备的未标较误差导致广播钟差和精密钟差存在一个基准差异,使评估的钟差误差带有一个常量基准偏差。相比于等效钟差改正数和广播钟差预报误差,广播星历中轨道预报误差具有更小的量级,为厘米级。
为了进一步分析图中的常量偏差,利用空间信号误差(SISure)来对其进行评估:
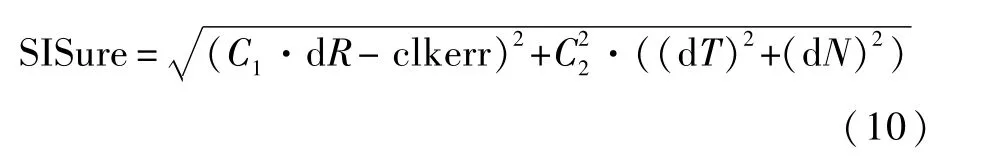
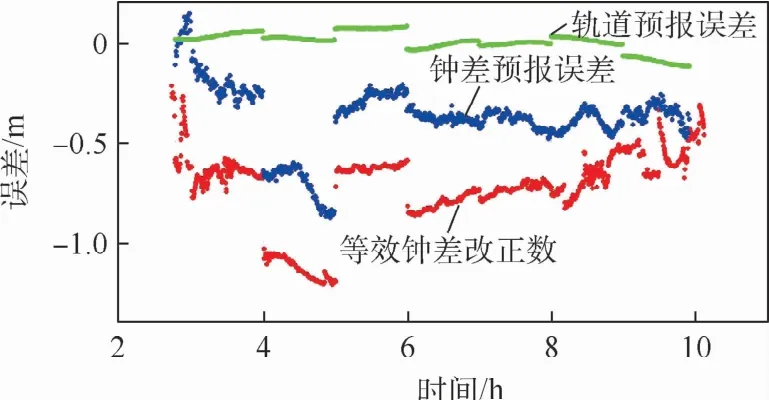
图2 C20卫星的等效钟差改正数与导航电文误差序列Fig.2 Time series of equivalent clock correction and navigation message error of satellite C20
图3(a)给出了等效钟差改正数、SISure与用户等效距离误差UERE的比较,选取C23卫星为代表,可以看出,同一天中出现了2种不同的现象,在前4 h中,也就是卫星第1次过境时,UERE与等效钟差改正数能够保持一致,但SISure则如广播钟差预报误差一样,与等效钟差改正数之间出现了一个常量偏差,而在该天的后4 h中,即卫星第2次过境时,SISure又与等效钟差改正数很好地重合在了一起,经过分析发现,这是由于在2次过境中间时间段双向时间同步跟踪卫星的天线设备发生过一次切换,卫星在第1次过境时,双向时间同步设备存在未标较误差,而在第2次过境时,地面更换了时间同步跟踪天线,由于该天线时间同步观测设备的系统误差得到更精准的标较,从而消除了广播钟差与精密钟差之间的基准偏差,因而出现了上述先分离后重合的现象,也可以看出,采用伪距解算的卫星UERE与等效钟差改正数更为一致,可以更好地体现广播电文引起的真实误差。
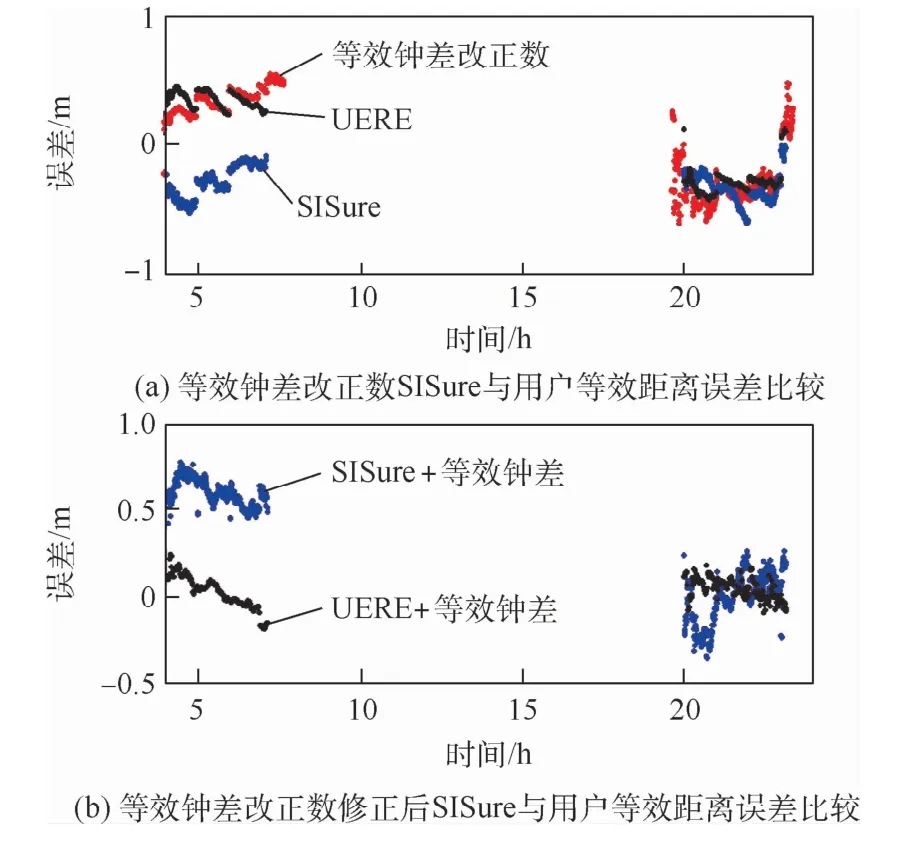
图3 C23卫星的等效钟差改正数与其广播钟差预报误差的比较Fig.3 Comparison of equivalent clock correction and prediction error of broadcast clock of satellite C23
图3(b)给出了等效钟差改正数修正后SISure和UERE的比较,可以看到与图3(a)中相一致的分离现象,同时可以看到,经等效钟差改正数修正后的UERE时间序列在0上下波动,结合图2,对于BDS-3卫星,等效钟差可以很好地修正以广播钟差误差为主的预报误差。
为了评估等效钟差改正精度,计算用户差分距离误差UDRE,并与基本导航服务的用户等效距离误差UERE进行比较。UERE和UDRE的计算方法可参见文献[20],结合式(1),可以得到监测站j相对于卫星i的UERE与UDRE相互间的关系,UDRE为加入等效钟差改正数修正后的距离误差:
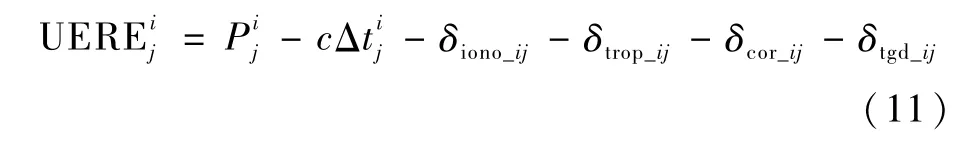
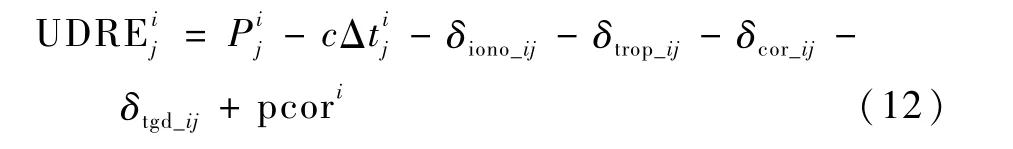
仍以C20卫星为例,图4给出C20卫星B1I/B3I频点的UERE和UDRE时间序列。可以看出,在没有经过等效钟差改正数修正前,C20卫星UERE约为1 m,经过等效钟差改正数修正后,C20卫星的UDRE接近零均值,说明等效钟差改正数正确地修正卫星的UERE。
图4中还可以看出,UERE在2019年10月26日4点期间误差明显变大,而UDRE仍保持不变,这说明等效钟差改正数可很好地修正空间信号误差。另外,虽然等效钟差改正数可以有效修正广播星历预报误差,但由于在卫星出入境时段观测噪声较大,且解算等效钟差时所用到的CNMC方法在卫星入境时需要一定的收敛时间才能获得较高精度的平滑伪距观测值,这就导致了等效钟差改正数在卫星出入境时段修正精度较低,因而从图4可以看到,UDRE曲线与UERE曲线在卫星出入境时较为接近。
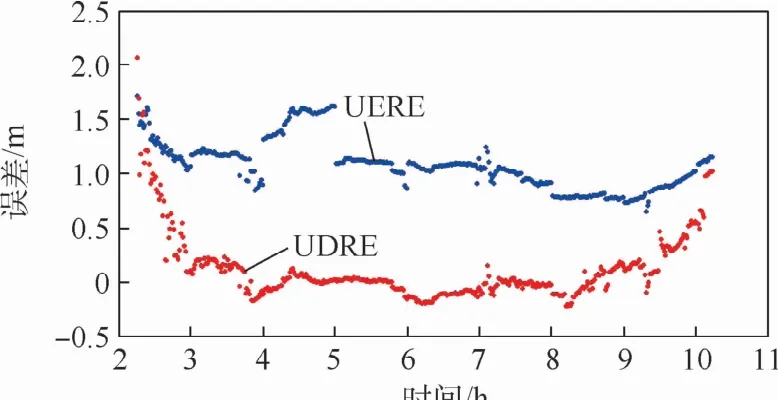
图4 C20卫星B1I/B3I频点UERE与UDRE对比Fig.4 Comparison of UERE and UDRE on B1I/B3I frequency point of satellite C20
对BDS-2和BDS-3各卫星的UERE和UDRE结果进行统计比较,如表4所示。可以看到,BDS-3卫星基本导航UERE平均在0.4 m,优于BDS-2卫星1.04 m;广域差分模式下,BDS-2卫星UDRE平均仅0.29 m,BDS-3卫星UDRE平均约为0.16 m。说明等效钟差改正数可以有效减小卫星的空间信号误差。
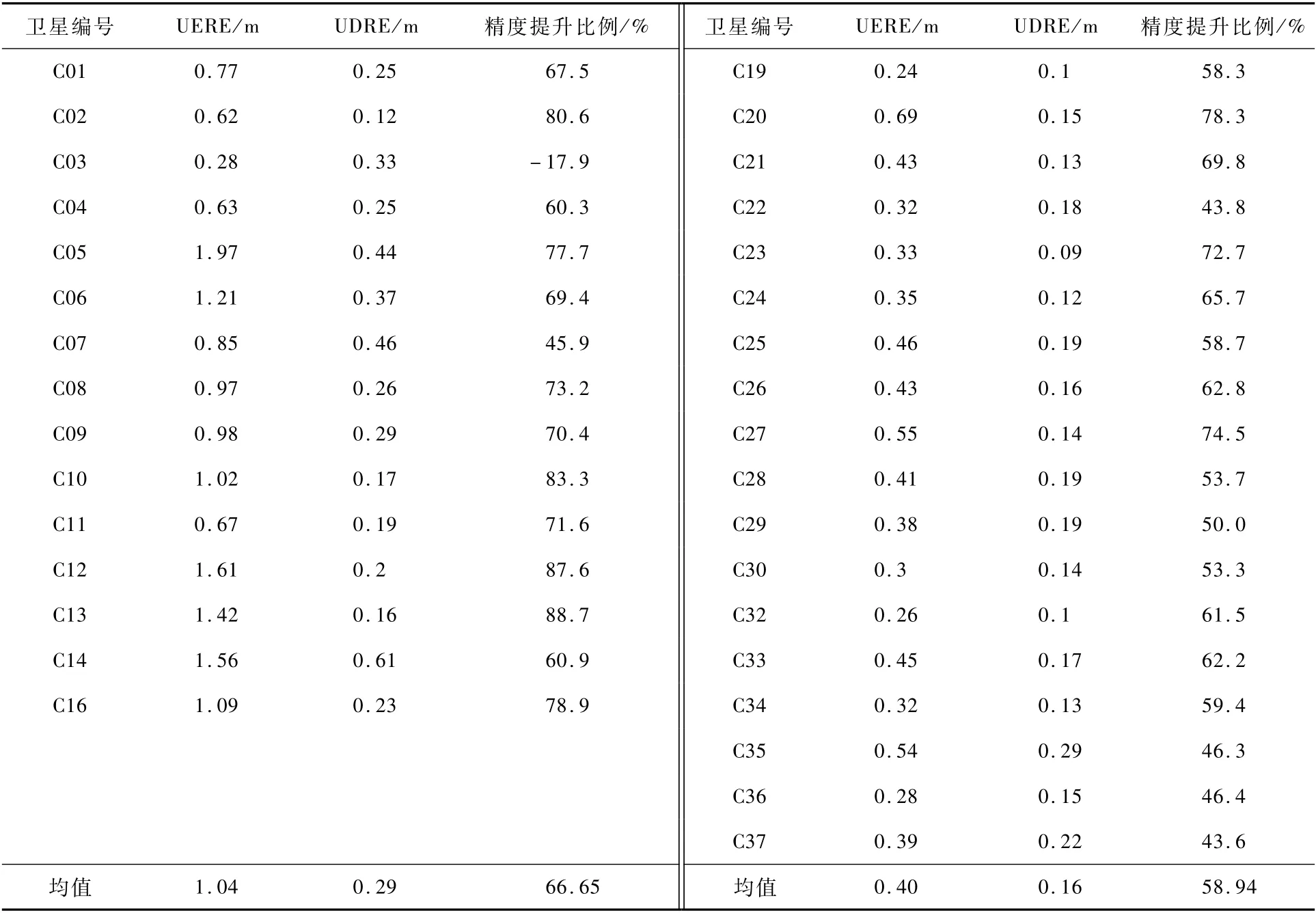
表4 北斗卫星UERE和UDRE统计Table 4 Statistics of UERE and UDRE for BDS satellites
2.2 格网点电离层垂直延迟改正数特征
与Klobuchar 8参数模型拟合解算电离层误差不同,广域差分服务中电离层误差是由服务区内格网点电离层垂直延迟改正数拟合得到。为研究格网点电离层垂直延迟改正数特性,本文以双频组合解算的电离层误差作为参考,对基本导航提供的Klobuchar 8参数模型和格网电离层模型2种方法的修正精度进行了对比分析。
实验首先基于2019年10月26日的格网点电离层垂直延迟改正数和Klobuchar 8参数以及B1I与B3I频点观测数据,对C01卫星(GEO)对地面监测站在穿刺点处B1I频点的电离层误差进行了分析,结果如图5所示。可以看出,电离层格网模型解算的电离层误差与双频组合解算的电离层误差具有更好的一致性,而采用Klobuchar 8参数电离层模型解算的电离层误差与以上两者相比均略有差异。经统计,以双频组合解算的电离层误差为参考,Klobuchar 8参数模型相比双频解算的电离层误差可修正77.17%,而格网点电离层垂直延迟改正数可修正95.76%,说明格网点电离层垂直延迟改正数解算结果相比Klobuchar 8参数模型可以更好地消除电离层误差,平均可提高18.59%。
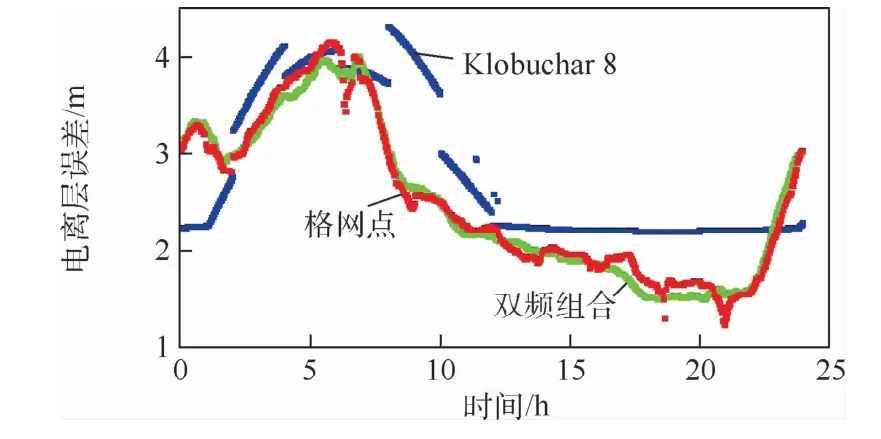
图5 三种模式下基于C01卫星B1I频点伪距解算的电离层误差Fig.5 Ionospheric error calculated based on the B1I pseudorange of C01 satellite in three modes
进一步,图6给出了分别采用Klobuchar 8参数和格网点电离层垂直延迟改正数修正后的UERE结果,并且为了只分析电离层误差对UERE的影响,限定2种模式的UERE都提前进行了等效钟差改正。可以看出,与Klobuchar 8参数模型相比,格网模型对UERE修正具有更高的精度,格网模型修正后的UERE仅为0.32 m,而Klobuchar 8参数模型为0.78 m。
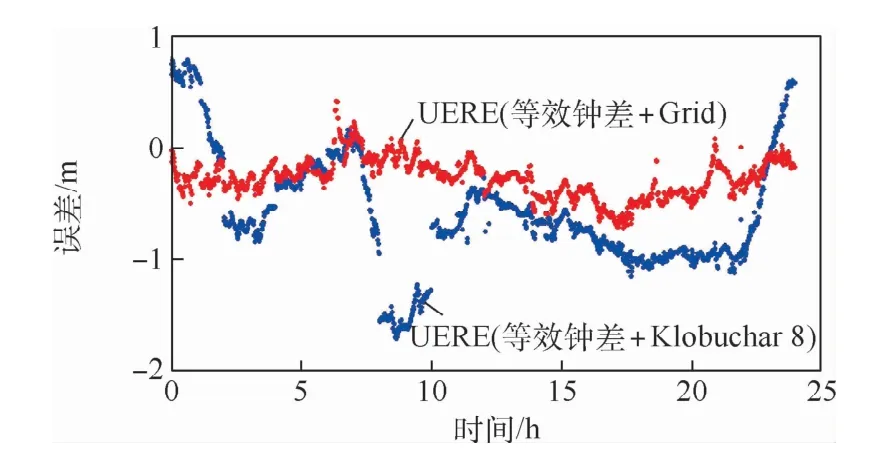
图6 两种模式下的C01卫星的UEREFig.6 UERE of C01 satellite in two modes
3 广域差分定位精度评估
BDS-3在设计上保留了B1I和B3I频点,实现与BDS-2的平稳过渡,可以更好地服务于北斗广域差分用户。BDS-3卫星的加入可以明显改善广域差分服务区域内北斗卫星的几何分布,从而提高服务精度。本文选取了2019年12月1日至12月8日服务区中部监测站的观测数据,对比分析了仅BDS-2卫星以及加入BDS-3卫星后的几何分布特征(PDOP)变化,结果如图7所示。可以看到,加入BDS-3卫星后PDOP值由2.46降低至1.76。
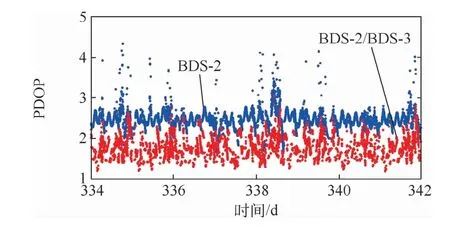
图7 四川某站观测北斗卫星空间几何分布Fig.7 Geospatial distribution of BDS satellite observed in one station of Sichuan
卫星导航定位精度受卫星几何构型影响的同时,还受限于卫星空间信号精度的影响,由表4可以了解到BDS-3卫星较BDS-2卫星在空间信号精度上有了进一步提升,可以为北斗用户提供更优质的服务。由此,选择在中国境内均匀分布的10个监测站,分别命名为STA1~STA10,获取2019年12月1日至12月14日连续14天的监测站观测数据以及相应的广域差分改正数,求解仅BDS-2卫星以及加入BDS-3卫星后基本导航和广域差分服务下B1I单频以及B1I/B3I双频定位精度,结果分别如表5和表6所示,并在图8和图9中分别给出了不同情况下水平和高程的定位精度(95%置信度)统计柱状图。
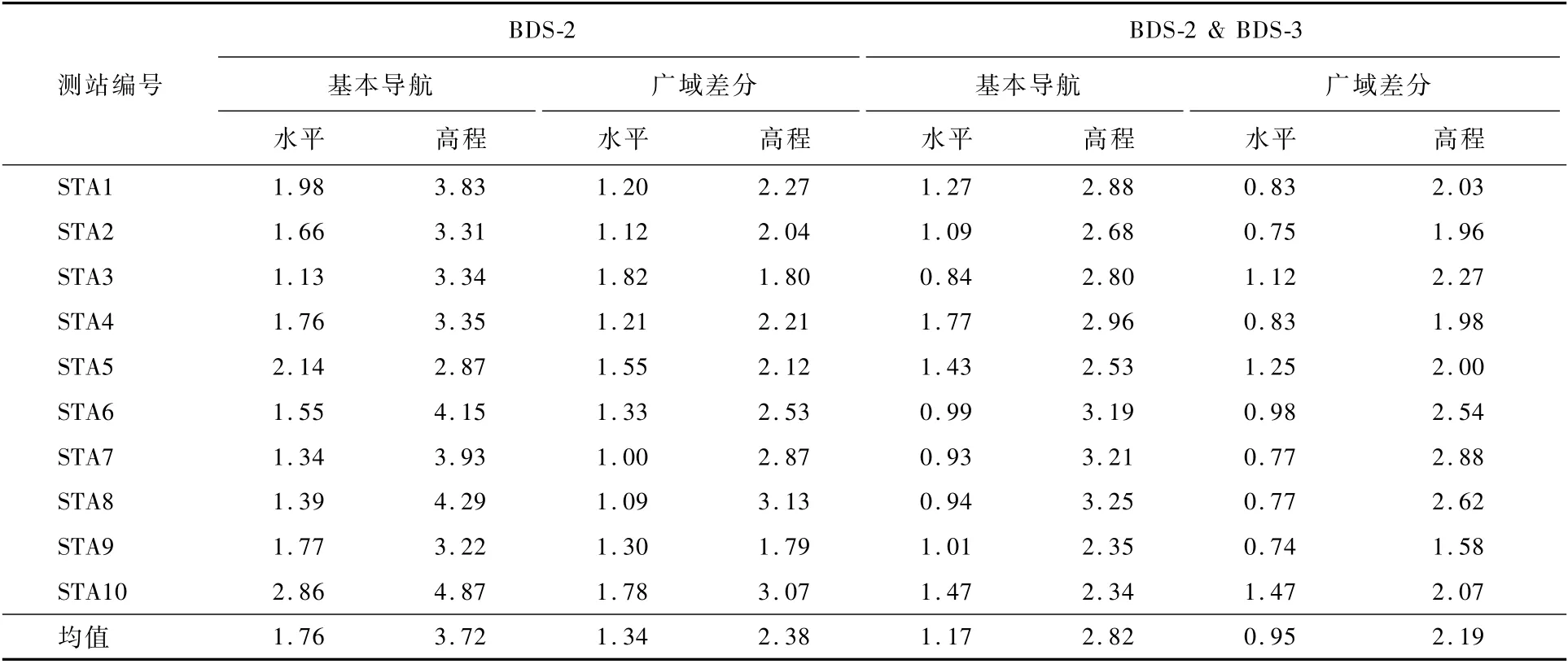
表5 仅BDS-2和BDS-2/BDS-3的基本导航与广域差分单频定位结果统计Table 5 Statistics of single-frequency positioning results on two modes of basic navigation and wide-areadiffer ential for single BDS-2 and combination of BDS-2/BDS-3 m
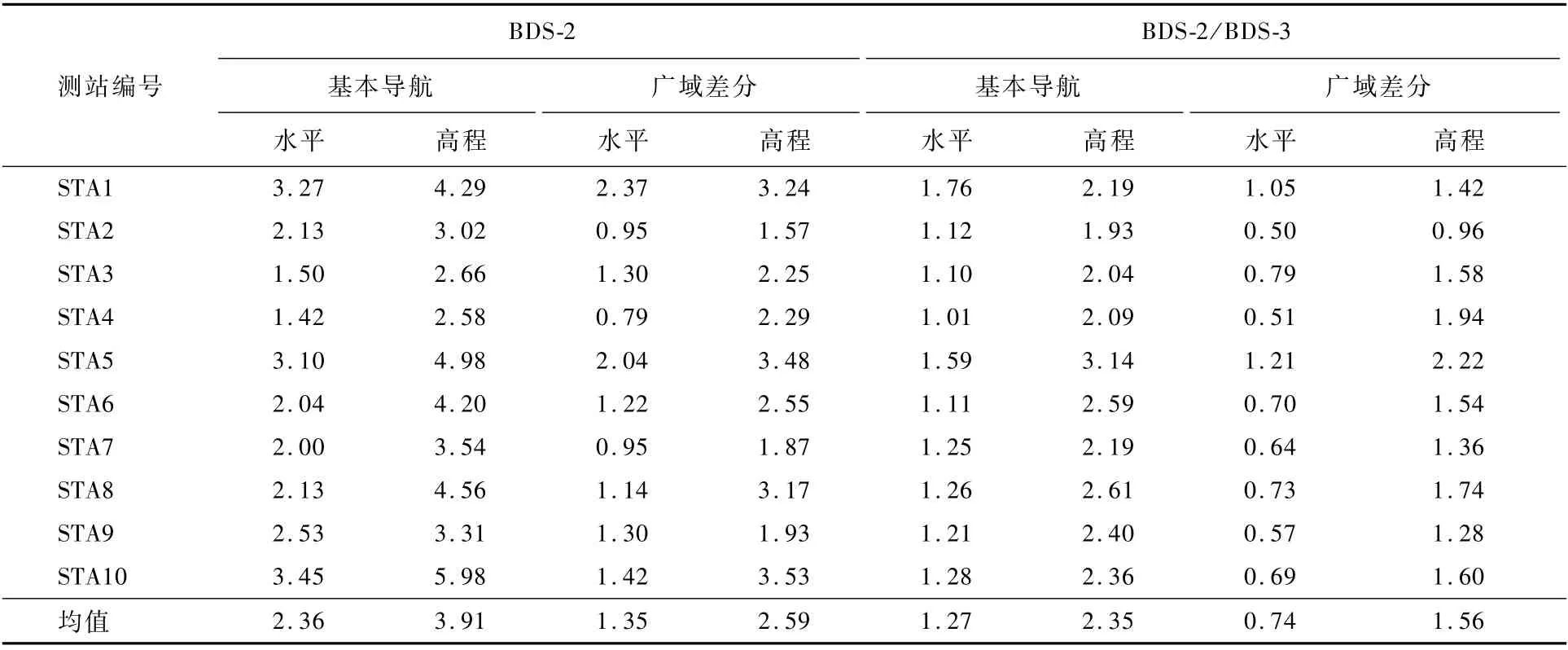
表6 仅BDS-2和BDS-2/BDS-3的基本导航与广域差分双频定位结果统计Table 6 Statistics of dual-frequency positioning results on two modes of basic navigation and wide-area differ ential for single BDS-2 and combination of BDS-2/BDS-3 m
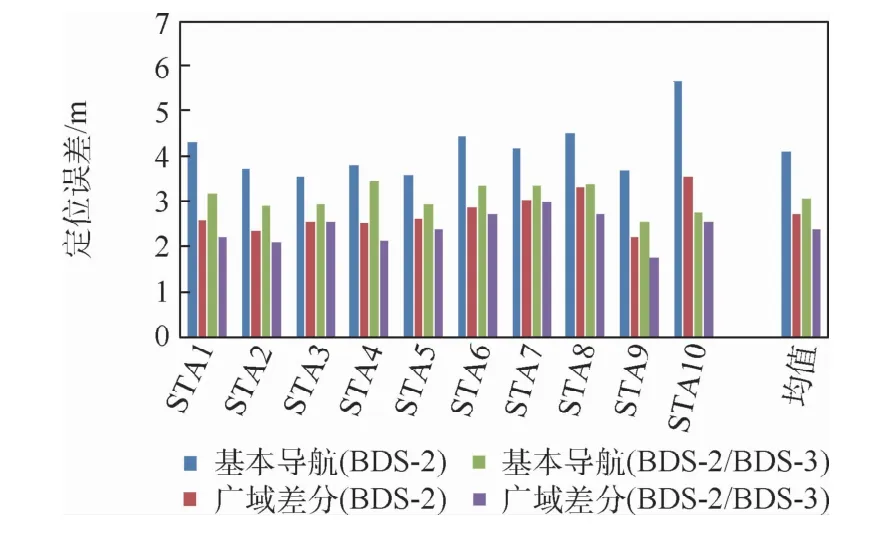
图8 四种模式下B1I单频定位精度Fig.8 Accuracy statistics of single-frequency positioning on B1I in four modes
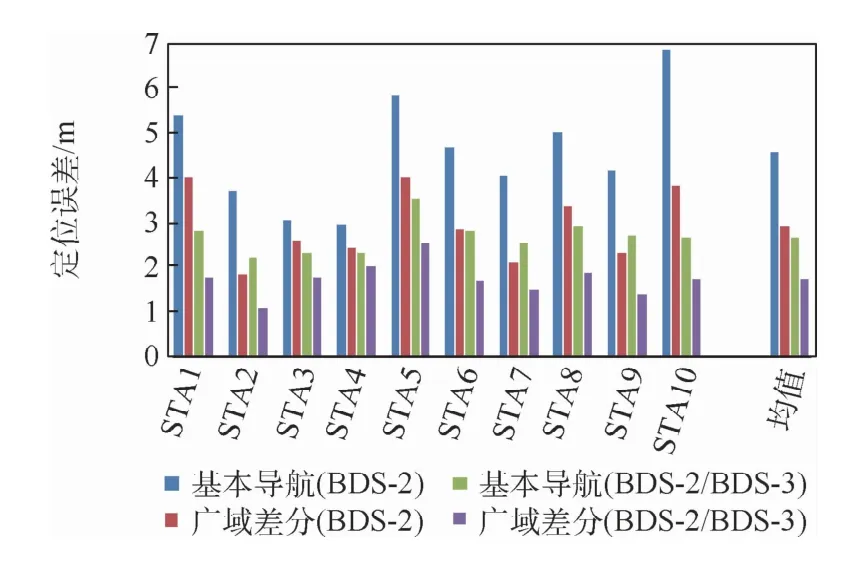
图9 四种模式下B1I/B3I双频定位精度Fig.9 Accuracy statistics of dual-frequency positioning on B1I/B3I in 4 modes
结合图表可以明显看到:①基本导航模式下,加入BDS-3卫星后定位精度有显著提升,B1I单频定位精度水平方向由1.76 m提高到1.17 m,高程方向由3.72 m提高到2.82 m,高程平均可提升24%,B1I/B3I双频定位水平精度由2.36 m提高至1.27 m,高程由3.91 m提高至2.35 m,平均可提升42%。②广域差分模式下,加入BDS-3卫星后定位精度也有提升,单频定位水平由1.34 m提升至0.95 m,高程由2.38 m提升至2.19 m,高程平均提升8%;双频定位水平由1.35 m提升至0.74 m,高程由2.59 m提升至1.56 m,平均可提升40%。在具有相同卫星数的条件下,广域差分服务相比基本导航定位精度有一定提升,如在BDS-2/BDS-3组合定位中,单频定位精度水平方向由1.17 m提高到了0.95 m,高程方向由2.82 m提高到2.19 m,高程平均可提升22%;B1I/B3I双频定位精度水平方向由1.27 m提高至0.74 m,高程方向由2.35 m提高至1.56 m,平均可提升34%。通过以上比较可以得出结论,加入BDS-3卫星后,定位精度会显著提高,而相比于基本导航,加入各项改正后的广域差分服务的定位精度则有明显提升。
4 结 论
本文利用中国服务区域内多台监测站的实测数据对北斗广域差分系统的定位服务精度进行了评估,分别讨论了等效钟差改正数和格网点电离层垂直延迟改正数的误差修正特性,得到如下结论:
1)BDS-3卫星的广播星历中轨道预报误差明显小于钟差预报误差,在基本导航模式下,BDS-2卫 星UERE为1.02 m,BDS-3卫 星 的UERE为0.4 m,在广域差分模式下,BDS-2卫星UDRE为0.29 m,BDS-3卫星的UERE为0.16 m,等效钟差改正数可以显著提高北斗卫星空间信号精度。
2)与基本导航提供的Klobuchar 8电离层改正模型相比,广域差分服务提供的格网电离层改正模型可将电离层延迟改正精度提高约18%。
3)与单独BDS-2卫星相比,BDS-2/BDS-3卫星联合条件下,基本导航服务单频和双频的定位精度分别为3.1 m和2.7 m,提升了26%和41%;广域差分服务单频和双频定位精度为2.4 m和1.7 m,分别提升了13%和41%。
4)广域差分模式下,单频和双频用户定位精度相比于基本导航分别提升22%和34%。
