基于博弈论综合赋权的学科竞赛对大学生创新能力培养评价研究

刘琪芳 张磊 贾丽艳

摘  要： 学科竞赛作为高校培养创新创业新型人才的有效载体，客观公正评价其对大学生创新能力培养的作用具有重要意义。文章从思维、素质、成果、效益四个方面选取16项指标，建立三层立体评价指标体系，在利用层次分析法和变异系数法确定多层评价指标的主、客观权重的基础上，引入博弈论Nash均衡基本思想，优化并确定指标因素的综合权重。研究结果表明，该方法有效地抑制了主观或客观因素引起的评价影响，明确学科竞赛更有利于提升解决问题B15、团队协作B22、沟通协调B23等方面的能力，指出了高校人才创新能力培养的新目标。

关键词： 学科竞赛; 层次分析法; 变异系数法; 博弈论; 创新能力评价

中图分类号：G645          文献标识码：A     文章编号：1006-8228（2021）01-68-04

Research on evaluation of the cultivation of discipline competition on college students'

innovation ability based on comprehensive weight of game theory

Liu Qifang1， Zhang Lei1， Jia Liyan2

（1. College of Information Science and Engineering， Shanxi Agricultural University， Jinzhong， Shanxi 030801， China;

2. College of Food Science and Engineering， Shanxi Agricultural University）

Abstract： Discipline competition is an effective carrier for cultivating innovative and entrepreneurial new talents in universities， an objective and fair evaluation of its role in cultivating innovation ability of college students is extremely important. This paper selects 16 indicators from four aspects of thinking， quality， results and benefit to establish a three-level three-dimensional evaluation index system. On the basis of determining the subjective and objective weights of multi-level evaluation indexes by using analytic hierarchy process and coefficient of variation method， Nash equilibrium idea of game theory is introduced to optimize and determine the comprehensive weight of index factors. The results show that this method can effectively suppress the influence on evaluation caused by subjective or objective factors， and make clear the discipline competition is more conducive to improving the abilities of problem solving B15， team cooperation B22， communication and coordination B23， etc.， which points out the new goal of talent innovation ability training in colleges and universities.

Key words： discipline competition; analytical hierarchy process; variation coefficient method; game theory; innovation ability evaluation

0 引言

高校学科竞赛是落实高校质量建设要求、培养创新人才、提高创新意识的重要渠道与手段之一，对大学生创新能力的评价研究属于多属性复杂性问题[1-2]。张鑫等学者利用层次分析法与MFCE法对创新创业能力水平进行综合评价并提出实施意见[3]。陈亚琼等学者以FAHP方法针对理工科类大学生创业能力开展指标体系与模糊综合评价[4]。吴婷等学者借助专家意見的层次分析法，实现大学生创新能力评价指标的重要程度确定[5]。权重作为评价类研究的重要指标，单一方法决定属性权重必将导致评价的片面性。因此，本文提出以层次分析法与变异系数法分别对学科竞赛创新能力评价系统中存在相互联系和相互制约的多因素复杂事物进行分析，构建独立基础权重集。在此基础上，运用博弈论理论分析其内在竞争关系，获得指标最优综合权重，为大学生创新能力的教育评估及决策提供理论依据。

1 构建创新能力评价指标体系

学科竞赛对大学生创新能力培养的评价存在很多的衡量因素。本文重点对高校在校及毕业两年内参加学科竞赛的学生为评价对象，以问卷调查方式累计数据。遵循排他性、科学性、可行性、全面性原则，在征得专家意见及深入调查、讨论、反馈后，将问卷评价内容分解为以创新能力为评价目标的目标层、准则层、指标层三层立体结构评价体系。各项指标以10分满分制进行评价。表1为建立的学科竞赛创新能力评价指标体系。

2 评价方法

2.1 层次分析法确定主观权重

层次分析法通过层次划分使各个评价因素有序，对每一层次因素的相对重要性进行对比，根据权重值进行指标影响排序。具体步骤如下。

⑴ 选取评价指标数值均值作为相对尺度进行两两交叉比较，构建各层判断矩阵

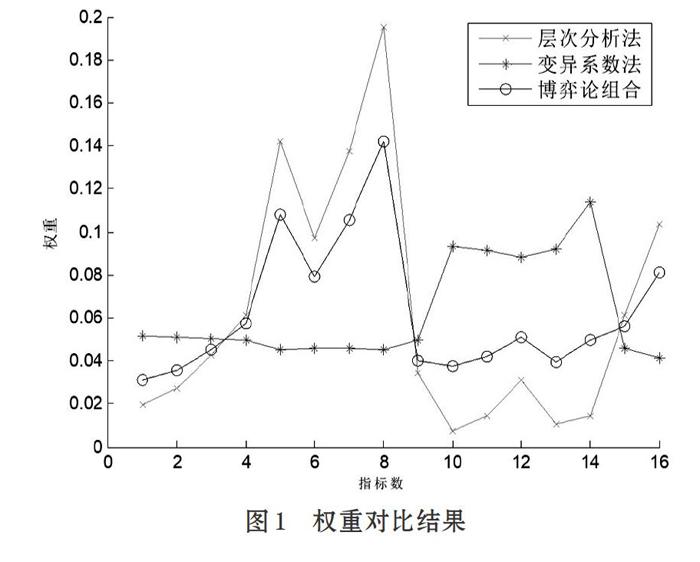
以指标层为例构造判断矩阵，设指标i评价数值均值为Vi，指标j评价数值均值为Vj，如果Vi

[f1=11/22152531/51/51/21/311/441f2=11/2211/31/31/41/21/31/432334421/21/4211/4441] ⑴

⑵ 计算归一化指标权重并求取判断矩阵的最大特征根[λmax]与一致性检验

[wi=（j=1maij）1m（j=1maij）1m （i，j=1，2，…，m）] ⑵

[CR=CI/RI] ⑶

其中，CI =（[λmax]-m）/（m-1），为偏移率一致性指标。RI为平均随机一致性指标，代表平均偏移率的平均一致性指标。利用MATLAB重复10000次进行随机判断矩阵计算结果如表4所示。

⑶ 计算多层指标权重

考虑准则层一级指标对指标因素的影響，计算综合权重为两级权重值得乘积。结果见表5所示。

从表6结果分析可得，表中CR均小于0.1，可以判断其构建矩阵合理有效，符合一致性要求。

2.2 变异系数法确定客观权重

变异系数法利用各项指标数据的标准差与均值直接计算得到指标权重[6]。指标数据差异变化与权重呈正比，即差异越大，权重越大，对评价结果影响越重要。具体计算方法如下：

⑴ 计算第i组指标变异系数

[Ci=σimi] ⑷

其中，[σi]为第i组指标数据的标准差，[mi]为第i组指标数据的算术平均值。

⑵ 利用多层各项指标的权重计算公式⑸所示，为其求得指标权重分配。

[wi=ViVi] ⑸

2.3 博弈论组合赋权法

博弈论分析方法寻找最优权重与各指标不同权重之间的极小化差值，获得最优评价指标权重[7]。其具体步骤如下：

⑴ 设学科竞赛创新能力评价指标基本权重向量集wk={wk1，wk2，…，wkm}，k=1，2，…，L，其中wk为第k种赋权方法确定的权重集合，m为评价指标数量。本文L=2，m=16。设a={a1，a2}为线性组合系数，综合权重向量w满足为两个向量的任意线性组合为：

[w=k=1Lak?wTk]（ak>0）  ⑹

⑵ 优化两个个权重向量的权值向量ak，以w与wk的极差最小化，得到最优权值w*，即优化目标函数为：

[minak>0k=12ak?wTk-wk2] ⑺

⑶ 按照矩阵微分性质得到目标函数对应的线性方程组形式

[w1?wT1w1?wT2w2?wT1w2?wT2a1a2=w1?wT1w2?wT2]  ⑻

求解矩阵式⑻得组合系数a1=0.4377、a2=0.8028，归一化处理得权值向量[a*1]=0.3528、[a*2]=0.6472，最终评价指标组合综合权重。

[w*=k=12a*k?wTk]  ⑼

利用MATLAB进行权重计算组合综合权重，如表7所示。

从表7可知，指标要素B15、B22、B23权重较大，B21、B43权重次之，其余甚次之。对比2017-2020年间学科竞赛实际调研及统计结果，实例说明学科竞赛影响大学生创新能力的主要指标因素为解决问题的能力、团队协作能力、沟通协调能力，而通过学科竞赛产出的创新成果与效益的方面较为薄弱，与学生成果主观转换意识相对较薄弱，知识能力积累不够全面有一定的关联。

图1为评价方法权重结果曲线图。分析可得：受主观因素与指标要素关联性影响，层次分析法突出了能力因素的权重，削弱了效益因素结果的权重;变异系数法对指标要素原始样本数据进行分析，其中科技创新成果与科技教育效益两个准则层的波动较大，突出了效益因素结果的权重;基于极小化差均衡理论的博弈论组合权重法求取的权重结果位于两者之间，16项指标因素权重得到了一定的平衡，一定程度减少了因主观或客观因素引起的影响，获得了相对较优的权重结果。

3 结束语

针对以往研究学科竞赛对大学生创新能力培养方面的评价方法单一、主观性强、解释性弱等问题，从主观评价指标与客观评价指标构建入手，以博弈论思想为基础，均衡主观赋权与客观赋权权重集，确定了综合最优权重结果。针对上述理论结果，提出大学生创新能力提升建议：营造实践创新个性发展的宽松学习环境，鼓励学生了解科技前沿技术，凝练科学研究问题，提出创新性想法和观点;搭建多层次开放式的发展平台，为学生实际实践动手提供良好的环境;强化创新创业专业教师的能力提高，为学生创新能力培养发展护航。此外，应重视培养学生创新思想意识及实践能力，加强知识能力积累，提升成果转化思想，把每个培养环节落到实处。

参考文献（References）：

[1] 李春阳，郑艺，付铁等.基于学科竞赛的实践教学模式研究与实践[J].实验技术与管理，2019.36（10）：208-210

[2] 陶剑飞，梁军.以学科竞赛为抓手提升大学生创新创业能力[J].高教论坛，2016.12（12）：40-42

[3] 张鑫，史文文，傅为忠.基于MFCE法的大学生创新创业能力评价研究—以合肥工业大学为例[J].创新与创业教育，2019.10（2）：57-61

[4] 陈亚琼，吴文博.基于模糊层次分析法的理工科大学生创业能力评价研究[J].湖南工程学院学报（自然科学版），2019.29（04）：49-53

[5] 吴婷，曾一帆，曾立基.基于AHP的应用型高校大学生创新创业能力评价研究[J].江西青年职业学院学报，2015.6：21-24

[6] 严嘉伦，林俊光，楼可炜等.基于AHP-变异系数法的楼宇型综合能源系统评价体系[J].热力发电，2019.48（12）：25-30

[7] 郭燕红，邵东国，刘玉龙，陈述.工程建设效果后评价博弈论集对分析模型的建立与应用[J].农业工程学报，2015.31（9）：5-12

收稿日期：2020-07-29

基金项目：山西省教育科学“十三五”规划课题（GH-17009）; 山西省高等学校教学改革创新项目（J2018024，J2019062）; 山西省研究生教育改革项目（2020YJJG108）; 山西农业大学双语教学项目

作者简介：刘琪芳（1981-），女，山西太谷人，博士，副教授，研究生导师，主要研究方向：农业信息化与工程技术。