数学实验：跨界联结视域下的创新力培养

吴恢銮 吕琼华

【摘 要】“如何估测树叶的面积”是在人教版数学五年级上册“估测不规则图形面积”基础上设计的统计概率类数学实验内容，旨在让学生经历“提出问题—实验猜想—实验验证—实验反思”跨领域解决问题的过程中，探索随机数据和面积的联系，体验转化、随机等数学思想，培养学生“跨界研究”问题的创新意识和实验能力。

【关键词】跨界联结 真实性问题 创新力

一.课前慎思

乔布斯曾经说过，创新就是把不同的事物联系起来。

数学家皮埃尔·德利涅曾说过：“在数学中，当你发现两个看似没有共同之处的东西事实上相互关联是一种乐趣，而在两个问题之间建立一个支点则是一个强大的工具。”

可见，数学学习中能把不同领域的知识、方法和思想关联融合，让学生探索跨领域、跨学科知识间的内在联系，不仅可以提升学生解决真实问题的能力，更是在培养学生的创新力。

解决非常规性数学问题作为一种高级的智力活动，从问题的产生到解决，牵涉到许多更高层次的心理活动过程，其中不同知识领域与不同思维方式的“跨界联结”，是学生实践能力与创新思维的有力体现。我们如何借助数学实验这种学习方式，通过非常规性数学问题的解决，来引领学生实现不同知识领域的“跨界联结”呢？

“如何估测树叶的面积”是笔者在人教版数学五年级上册“估测不规则图形面积”的基础上设计的拓展类数学实验内容，旨在让学生在经历“提出问题—实验猜想—实验验证—实验反思”跨领域解决问题的过程中，探索随机数据和面积的关联，体验转化、随机等数学思想，进而培养学生“跨界研究”问题的思想意识和创新力。

二、课堂再现

（一）任务驱动，提出问题

1.提出问题

师：根据课件（见图1），你能提出什么数学问题？

学生提出的问题有：

（1）长方形面积是多少？

（2）树叶的面积是多少？

（3）树叶的周长是多少？

（4）长方形面積是树叶面积的几倍？

（5）树叶面积是长方形面积的几分之几？

（6）空白部分的面积是多少？

师：请同学们把这些问题分一分类？

（学生把问题分成两类：一类求面积，一类求周长）

2.筛选问题

师：今天这节课我们先来研究树叶的面积。有哪些方法可以估计树叶的面积呢？

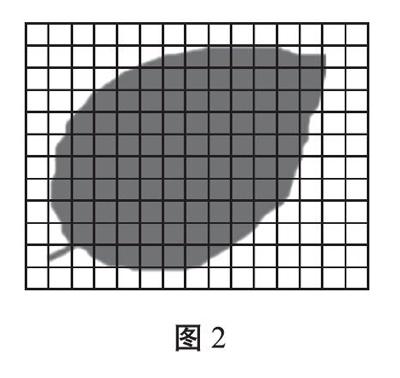
生：我将长方形分割成单位面积的小正方形（见图2），通过数小正方形的方法估测面积。这里可以把小方格分为两类：一类是整格的，另一类是不满一格的。不满一格的都按半格计算。

师：用数格子的方法，而且能把格子分成整格和不是整格两类，再进行统计计算，想法很好。

生：我是把树叶转化成我们已经学过的正方形来估计面积的。

师：你用转化算，用到转化思想，真不错。

3.任务驱动

师：同学们想到了分类数和转化算这两种方法估测树叶的面积，很不错。不过，如果没有格子图，只是给你们每个小组提供了一盒绿豆（见图4），你能想出新的方法来估测树叶的面积吗？

（二）探索尝试，设计实验

1.探寻方法

（1）你能利用这些材料创设出新的方法来求树叶的面积吗？

（2）小组交流：玩一玩，议一议。

2.方法交流

方法1：直接铺设法。

生：我们小组想先用绿豆填满树叶（见图5），然后数出绿豆的数量，估计出一颗绿豆底部的大小，再用一颗绿豆的底面积乘绿豆的数量来推测树叶的面积。

师：想一想，用这种方法估测树叶可能会碰到什么困难？

生：绿豆很难数，绿豆并不是一个规则的立体，底面面积很难计算。

方法2：铺满转化法。

师：我们小组先将绿豆铺满整张树叶（见图6），然后把这些绿豆摆成一个长方形，现在只要量出这个长方形的长和宽，就能计算出长方形的面积，也就推测出了树叶的面积。

师：你们觉得这个办法怎么样？

生：我觉得这个方法将不规则的树叶转化为规则的长方形图形，这样就解决了估测一粒绿豆底面积不准的问题，可以更加精确、更加方便地计算出树叶的面积。

方法3.撒绿豆实验法。

生：我们组的方法与大家很不同，我们想到在树叶上空撒下一把绿豆，绿豆就会散布在长方形里，然后我们再数出长方形里面和树叶上的绿豆的数量，看看两部分数量有怎样的倍数关系，它们的面积也应该具有这样的倍数关系。因为长方形的长和宽可以测量，可以计算出长方形的面积，然后就可以根据倍数关系计算出树叶的面积了。

师：这种方法很特别，大家听能明白吗？他们这一组采用的是什么方法？

生：他们想用图形中绿豆分布的数量关系来推测树叶面积与整个长方形之间的关系。

师：你们是怎么想到用撒绿豆这种方法的？

生：老师，我们盒子里的绿豆很少，不够铺满整片树叶，我们只好想到用撒绿豆的方法来粗略地估测树叶的面积。

师：大家评价一下这种方法到底能不能估测出树叶的面积呢？

生1：如果只撒一次，撒不均匀，怎么办？

生2：撒一次可能不够，可以多撒几次，每次尽量撒得均匀，我觉得这样的话，可以试一试。

生3：这种方法我们以前从来没有遇到过，可以先试一试，做一做实验，然后再下结论行还是不行。

师：大家的思考和评估非常理性，不轻易相信一种方法，也不轻易否定一种方法，而是通过尝试后，用事实说话，很好。我们可以试一试做实验。想一想，我们在做撒绿豆实验时可能会遇到什么问题？你们试一试后再来交流。

3.规范实验

生1：为了解决撒得不太均衡的问题，我们小组通过实验后总结出了一些经验。首先，撒绿豆的高度在10厘米最好，其次，要居中撒下来，力度不能太重，也不能太轻，自然撒落最好。

生2：我还有补充，筐要放平，不能摇动。绿豆要抓一小把，一次性自由撒落。

生3：为了避免出现偶然性，我们组认为要多做几次实验。

生4：用大数据来推测会比较准确。

师：通过尝试和实验，大家从撒绿豆的高度、位置、力度等方面总结出了怎么撒比较均衡，还领悟到了一个重要思想方法，就是要多撒几次，把偶然性降低。

（三）实验实施，检验方法

1.实验要求

师：怎么随机撒绿豆，怎么统计绿豆，也就是说怎么做一个比较规范的实验，大家已经清楚了，现在请大家小组合作做实验。做实验时，要注意以下几个问题。

（1）撒豆：四人小组，大家轮流撒绿豆。

（2）记录：每撒一次，统计员就要记录数据。

（3）计算：最后算出几次实验的总数据。

2.实验实施

全班分为10个小组，每人参与实验过程。

3.实验数据

收集全班数据，并利用Excel表格（见表1）把数据转化为条形统计图（见图7）。

4.分析数据

师：你有什么发现？又有什么猜想？

生：长方形内绿豆数量是树叶图形内绿豆数量的2倍左右。我猜想，长方形的面积是树叶面积的2倍左右。

师：我们来测量一下长方形的长和宽，长是15厘米，宽是12厘米，根据这个猜想，请你推测出树叶的面积。

生：15×12÷2≈90（平方厘米）。

5.实验验证

师：到底猜想是否正确呢？我们还需要去验证。你打算怎样验证？

生：我们可以用以前学过的分类数和转化算的方法来验证。

师生活动后，组织反馈。

生1：我用分类数的方法得到的面积大约是89平方厘米。

生2：我用转化算的方法，得到面积大约是90平方厘米。

6.实验结论

用撒绿豆的实验方法，获得实验数据后，计算出长方形和树叶上绿豆数量的倍数关系，根据它们数量的倍数关系可以推测出这两种图形的面积关系，从而推算出树叶的面积。

（四）實验反思，揭示原理

1.实验反思

师：为了区别于分类数、转化算，今天这个方法可以取什么名称？

生：可以取名“实验估”。

师：比较这三种估测树叶面积的方法，你有什么想说的？

出示图8。

生1：如果有格子图的话，转化算比较简单，但是结果不一定准确;分类数比较准确，但是数比较麻烦。

生2：如果没有格子图，我们可以用绿豆或者大米、黄豆这些东西，通过做实验来推测不规则图形的面积。但做实验要注意撒得均匀，做的次数要多一些。

师：我们已经会用分类数、转化算来估计不规则图形的面积了，为什么这节课还要去发明“实验估”这种方法呢？

生1：可能性和几何图形的面积联系起来，我们以前没有做过。原来用随机实验可以推测出树叶面积，很神奇。

生2：这节课我们学会了解决问题的一种新方法：发现问题，提出问题，然后做实验又发现问题，形成猜想，最后验证猜想是否正确。

师：苹果手机的创始人乔布斯曾经说过一句话，创新就是把不同的事物联系起来。这节课我们用统计概率的思想去解决面积问题，就是把不同领域的知识与思想方法联系起来，这是一种创新，我们在做一件跨界思考的事。

2.揭示原理

师：其实早在几百年前，就有了这样的方法。我们来了解一下实验原理。

阅读材料：蒙特卡洛法。

考虑平面上一个边长为1的正方形及其内部一个形状不规则的“图形”，如何求出这个“图形”的面积呢？蒙特卡洛法是这样一种“随机化”的方法：向该正方形“随机地”投掷a个点落于“图形”内，有b个点落入这个不规则图形中，则该“图形”的面积近似为b/a。

师：如果你对这个蒙特卡洛实验法感兴趣，课后可以上网进一步去了解和学习，还可以进一步思考，这个实验法还可以帮助我们解决哪些实际问题？

三、课后再思

如何测量树叶的面积，学生在经历了第一段借助方格图估算树叶的面积外，面对没有方格图，仅借助绿豆，能否想到新的方法去解决。“实验估”把“统计概率”与“几何面积”联系了起来，实现了思维的跨界，这种方法的价值不在于是否“实用”，而在于思维方式的创新，像这样具有探究性、拓展性的实验内容，学生不仅学会了问题解决的策略与方法，更是丰富了数学经验，发展了数学能力，拓宽了数学思想。由此可见，“跨学科课程”要让学生真实地融入问题情境之中，在高认知水平的数学任务驱动下，激发学生学习的主动性和持久性，使数学实验更多指向创造性和批判性思维。

“跨界联结”视角下的数学实验学习要摆脱“一题、一例、一解”的处方化模式，要开放问题的探索空间，让学生可以从多角度提出问题，进而让学生筛选出有价值的问题。如利用绿豆，有办法估测出树叶的面积吗？这个问题探索空间就非常大，使得学生有机会经历“直接铺设法—密铺转化法—撒绿豆实验法”思维不断创新的过程，知识联结不断跨界的过程，从定向测量到转化度量，最终想到用统计概率的思想研究面积，使“面积”与“概率”两个不同领域的内容在思考与实践中实现了完美“跨界联结”，这一“跨界联结”不仅打通了学生的随机思想和定量思想的“任脉”，而且实现了思维方式的创新。

教师也不能简单地将学生封闭在“知”与“不知”的动态平衡上，而要延伸到整个实验活动的“问题”和“解决”空间上，使他们在实验探索中获得一次次良好的深度情感体验。如深度评估与反思“直接铺设法”“间接转化法”和“撒绿豆实验法”三种测量方法，完成实验探索后再对“分类数”“转化算”和“实验估”三种方法的比较体验，特别是对“实验估”的看法，有学生提出：“可能性和几何图形的面积联系起来，我们以前没有做过这样的思考。”这是学生深度参与学习后获得的深度反思。

总之，“跨界联结”视域下数学实验课要让学生的高阶认知与元认知协同发展，唯有这样，学生的创新力才能不断迸发。

【参考文献】

[1]安桂清.基于核心素养的整合：特征、形态与维度[J].课程·教材·教法，2018（9）.

[2]张景中，王鹏远.少年数学实验[M].北京：中国少年儿童出版社，2012.

[3]夏雪梅.项目化学习设计[M].北京：教育科学出版社，2018（11）.

[4]吴恢銮，张天孝.数学实验：让数学课好玩起来[J].小学数学教师，2017.