分岔隧道火灾烟气流动特性研究*

李智胜，蒋浩锴，高云骥，靳开颜，张玉春，李 涛

(西南交通大学 地球科学与环境工程学院，四川 成都 610031)

0 引言

随着经济的快速发展及社会需求的不断增加，我国城市基础建设规模逐年增大。截止到2019年底，我国公路隧道19 067处，全长1 896.66万m[1]。然而，由于隧道结构的狭长性及密闭性限制灭火和救援的机动性，且隧道火灾可能产生高温和有毒有害气体，严重威胁着隧道结构及人员生命安全。因此，近年来隧道火灾烟气流动特性备受国内外学者关注。

研究隧道顶棚温度分布规律作为研究烟气流动特性的重要手段已被广泛应用。顶棚最大温度是隧道火灾研究中的重要内容之一，有关研究表明大规模隧道火灾可能导致顶棚温度超过1 350 ℃[2]。Alpert[3]基于大尺寸非受限室内火灾实验，提出顶棚射流最大烟气温升预测模型，然而该模型仅适用于火源与侧壁间距大于1.8倍顶棚高度的火灾场景；Kurioka等[4]建立纵向通风条件下最大烟气温升经验模型，然而该模型不适用于风速趋近于0的条件；Li等[5]根据能量守恒及火羽流理论，提出顶棚下最大烟气温升预测模型，该模型准确性已被众多学者所证实。纵向温度分布是隧道火灾中另一重要研究内容，其可反映顶棚下方烟气的流动特性。Delichatsios[6]以竖直顶梁结构火灾为研究对象，提出顶棚下烟气温度纵向衰减经验模型。近年来，Hu等[7]基于全尺寸实验及理论分析，建立隧道火灾烟气单指数温度纵向衰减预测模型；Gong等[8]通过考虑热平衡方程，提出双指数温度纵向衰减预测模型。上述文献针对隧道火灾顶棚温度进行大量研究，然而大多假设的火灾场景发生在单洞隧道内。因此针对单洞隧道火灾烟气流动特性研究较多，然而关于分岔隧道火灾的报道较少[9-14]，Huang等[9]基于1∶20缩尺模型，通过考虑岔道角度对顶棚温度的影响，提出1个顶棚下最大烟气温升预测模型；Chen等[10]分析纵向通风对有无岔道工况下烟气流动特性的分布规律，结果表明岔道的存在对纵向温度的分布具有一定的影响。但上述研究大多假设火源发生在隧道中心位置。事实上，隧道火灾具有较大的随机性，可能发生在隧道内的任何位置[12]。

鉴于此，本文通过设置不同火灾场景，模拟火源位置及热释放速率对分岔隧道内烟气流动特性的影响规律，以期为隧道火灾研究提供数据支撑及指导建议。

1 数值模拟方法

1.1 比尺模型

比尺模型仿真实验在隧道火灾研究中已成为1种重要的研究方法，该方法优势在于可降低实验经济成本，同时可针对模型进行有效预测。其中弗鲁德尺寸准则能够对烟气的流动特性进行较好的预测，且文献[8-9]的研究也证实弗鲁德的准确性。因此本次仿真实验在1∶10缩尺分岔矩形顶棚隧道模型中进行。比尺模型与实际模型的关系可用式(1)～(4)表示：

(1)

(2)

(3)

(4)

式中：Tm为模型中的温度，K；Qm为模型中的热释放速率，kW；tm为模型中的燃烧时间，s；Tf为全尺寸中的温度，K；Qf为全尺寸中的热释放速率，kW；tf为全尺寸中的燃烧时间，s；Fr为弗鲁德数；V为纵向风速，m/s；g为重力加速度，m/s2，取值9.8 m/s2；H为隧道有效高度，m。

1.2 模型设置

以分岔隧道火灾为研究对象建立物理模型，其中主隧道长10 m，宽1 m，高0.6 m，岔道长度为5 m，岔道与主隧道水平夹角为45°，模型设置及热电偶布置如图1所示。

图1 分岔隧道结构示意

采用FDS软件进行仿真实验，网格大小为0.025 m，网格数量共计777 600个，其设置依据如式(5)～(6)所示[15]：

(5)

(6)

式中：Q为热释放速率，kW；D*为火源当量直径，m；ρ∞为空气密度，kg/m3；cp为比热容，J /(kg·℃)；T0为温度，℃；δx为网格尺寸大小；g为重力加速度。

为研究分岔隧道火源位置对烟气流动特性的影响，本文仿真实验在自然通风条件下进行，选取3个火源位置，分别布置在主隧道、分岔口及岔道内(如图1所示)。火源表面设置为burner，燃烧表面大小为0.2 m×0.2 m，热释放速率分别设置为7.9，15.9，23.9，31.9，39.9 kW。

2 结果与讨论

2.1 最大顶棚温度

为验证FDS在分岔隧道模拟烟气流动的有效性，选取2组实验工况进行对比，如图2所示。由图2可知，模拟值略高于实验值，但最大误差低于10%，因此此次仿真获取的烟气温度数据较为准确。不同火源位置下热释放速率对隧道顶棚最大温度的分布规律如图3所示。由图3可知，自然通风条件下3个火源位置对隧道顶棚最大温度影响较小，最大温差约为34 ℃。

图2 实验测试与模拟对比

图3 最大顶棚温度

2.2 岔道纵向温度分布规律

不同火源功率下火源位置对岔道内温度分布的影响规律如图4所示。由图4可知，火源上游一侧的温度明显低于下游一侧的温度，表明烟气倾向于岔道出口方向运移，同时也说明沿岔道纵向温度衰减速率存在一定的差异。此外，温度越高其衰减速率越快，且随着距离火源距离的增加，二者之间的差异逐渐减小，在距火源远处的区域内，温度分布差异较低，表明烟气流进入一维扩散阶段。

图4 岔道顶棚温度分布

选取火源下游侧0.5 m远处为参考点，对比不同火源位置下岔道顶棚温度分布规律，如图5所示。由图5可知，随着燃烧器远离岔道，其顶棚下最大温度明显降低，最大差值约为110 ℃。由此可见火源位置对分岔隧道纵向温度分布具有重要的影响，因此，有必要对岔道内温度纵向衰减系数进行修正。

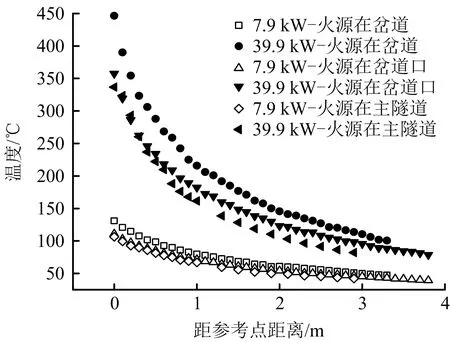
图5 不同火源位置岔道顶棚温度对比

分别采用Hu等[7]和Gong等[8]提出的温度纵向衰减预测模型对岔道内顶棚下无量纲温升与纵向距离的关系进行拟合，如图6所示。可以发现Gong等[8]的双指数预测模型显然更适合此次的模拟效果，且其相应的R2值分别为0.98，0.98和0.97，高于采用Hu等[7]的单指数模型拟合结果(R2值为0.89，0.92和0.92)。原因在于Hu等[7]忽略了空气横向卷吸对温度的影响。因此，后面的拟合公式将采用Gong提出的预测关系式。

图6 无量纲岔道顶棚温升

2.3 主隧道纵向温度分布规律

不同火源位置下主隧道上下游温度的对比情况如图7所示。由图7可知，火源位置位于主隧道及分岔口，距参考点距离D<1 m时，沿着隧道顶棚纵向的上游温度均大于下游温度，而D>1 m时，下游温度逐渐反超；随着烟气转变为一维蔓延模式时，这种差距逐渐降低。而当火源位置位于岔道时，D为3.75 m时，下游温度才逐渐反超上游温度，原因在于不同位置下分岔隧道结构对烟气的流动影响。由此可以看出，火源位置对纵向温度的衰减具有一定的影响。因此，需要对岔道内顶棚下温度衰减系数进行修正。

图7 主隧道顶棚温度纵向分布

为进一步了解分岔隧道上下游的烟气流动特性，需要对顶棚温度进行无量纲分析。Gong等[8]通过分析烟气的纵向蔓延流动特性，提出单洞隧道下双指数温升理论预测模型，其表达式如(7)所示：

(7)

式中：T0是环境温度，℃；ΔTx是距参考点x米处的温升，℃；w是隧道宽度，m；A，B，c，d是经验系数。

由于岔道的存在造成主隧道内上下游空气卷吸不对称，故导致其衰减速率有所不同。主隧道上下游无量纲温升与纵向距离的拟合关系如图8所示。以图8(c)为例，火源在岔道时，距离参考点0.5 m时，部分下游顶棚温度开始“反超”，随着烟气蔓延至3.25 m(距火源3.75 m)以上时，下游温度基本完全“反超”。这种情况与图7中变化规律较为一致。

图8 主隧道无量纲顶棚温升

3 结论

1)通过实验对比验证FDS模拟分岔隧道火灾烟气流动的准确性，其最大误差低于10%。

2)火源位置对火源上方最大温度影响较小，最大温差为34 ℃，然而火源位置对火源附近温度影响较大，其中距火源0.5 m处最大温差约为110 ℃。通过对比Gong等和Hu等提出的顶棚下温度纵向衰减预测模型拟合效果，发现Gong等提出的双指数模型准确性更高。

3)火源位置对烟气在主隧道流动过程具有一定的影响。通过对比主隧道内上下游温度的分布规律，发现不同程度的“反超现象”。火源位置在主隧道及岔道口时，距离火源1 m后基本全部出现“反超现象”，而对于火源位置在岔道时，“反超现象”出现在距火源约3.75 m处。