回采工作面瓦斯爆炸风门冲击载荷研究*

高建良，王文祺，吴泽琳，陈太东，蔡行行

(1.煤炭安全生产与清洁高效利用省部共建协同创新中心，河南 焦作 454003；2.河南理工大学 安全科学与工程学院，河南 焦作 454003；3.河南理工大学 河南省瓦斯地质与瓦斯治理重点实验室—省部共建国家重点实验室培育基地，河南 焦作 454003)

0 引言

煤矿井下开采技术进步及煤矿开采深度的加深导致瓦斯涌出量增加，瓦斯积聚和超限所引发瓦斯爆炸的概率也随之增大[1-2]。在瓦斯爆炸事故中，回采工作面上隅角瓦斯积聚引发瓦斯爆炸所占比例较大，其产生的冲击波将沿着回风巷等巷道传播。进入回风巷的冲击波将会摧毁回风巷与运输巷、行人巷之间的风门，从而进入运输巷、行人巷以及下一个工作地点。因发生瓦斯爆炸后风门的破坏可能会造成风流紊乱及人员伤亡，故研究瓦斯爆炸情况下，风门所受的冲击载荷变化规律意义重大，且可为减少瓦斯爆炸后的灾害损失提供依据。

由于矿井瓦斯爆炸实验需要较多的人力、物力去完成。因此，大量学者使用数值模拟方式对煤矿瓦斯爆炸过程进行研究。Gao等[3]利用CFD软件建立瓦斯爆炸的数值模型，研究火焰和激波的传播特性；赵军凯等[4]、庞磊等[5]、马秋菊等[6]借助计算流体力学软件Fluent研究得出，在体积分数为9.5%的瓦斯气体爆炸过程中，火焰传播速度、超压和温度均最大；冯路阳[7]运用Fluent软件对不同浓度下的瓦斯爆炸过程进行研究得出，管道中瓦斯爆炸温度值随着管径的增大而增大，密闭条件下瓦斯爆炸后管道内各点的压力值大小分布较为均匀；孟亦飞等[8]、徐阿猛等[9]利用Fluent软件研究得出，障碍物的存在可改变通风管网内未燃瓦斯的积聚区域，随着障碍物尺寸的增加，爆炸超压峰值也随之增加；朱邵飞等[10]采用流固耦合算法，了解瓦斯爆炸冲击波的衰减过程，并发现在受限空间会发生反射与叠加的现象；江丙友等[11]运用AutoReaGas软件模拟得出，冲击波在采煤工作面首尾相连巷网中传播时，冲击波超压最大值和最高温度持续减小，向同一方向传播的2个冲击波由于叠加效应，超压显著增大；邓照玉[12]、程卫民等[13]利用ANSYS/LS-DYNA研究瓦斯爆炸对巷道的破坏效应得出，在巷道壁面边缘位置和中心位置超压测值越大，其壁面损伤相对越严重，风门门垛最薄弱位置就是风筒所在位置；朱传杰等[14]研究封闭型管道内瓦斯爆炸的传播特征，结果表明闭口型系统内的瓦斯爆炸呈明显的振荡特征；高科等[15]借助开源化学动力学软件Cantera研究瓦斯爆炸特性的影响因素得出，在冲击波诱导瓦斯爆炸中，点火延迟时间随着瓦斯体积分数的增大而出现增大现象，随冲击波强度的增大而降低。

上述研究主要是针对不同因素对瓦斯爆炸冲击波的强度、特征及超压变化的影响进行研究，但对瓦斯爆炸后风门等通风构筑物的研究不足。本文结合羊场湾矿井Ⅱ020612回采工作面的实际情况，对在风门无破坏的情况下，工作面上隅角不同体积的瓦斯爆炸后冲击波传播过程开展模拟研究。研究结果可为煤矿井下风门的设计提供理论基础。

1 瓦斯爆炸计算模型的建立

1.1 回采工作面风门布置概况

羊场湾Ⅱ020612回采工作面巷道为U型布置，由采区轨道下山、采区运人下山、回采工作面进风巷、回采工作面回风巷、采区回风下山构成，在回风巷及进风巷的另一端计划开设进风巷综掘面以及回风巷综掘面。

回采工作面布置中有3处风门，作用分别为隔绝回采工作面回风巷与采区轨道下山的风流(称为风门a)、隔绝回采工作面进风巷与回采工作面进风巷综掘面风流(称为风门b)、隔绝采区运人下山、采区轨道下山以及回采工作面进风巷综掘面风流(称为风门c)。风门a位于回采工作面回风巷支路中，风门b位于回采工作面进风巷中，风门c位于回采工作面进风巷支路中。Ⅱ020612回采工作面巷道布置如图1所示。

图1 Ⅱ020612回采工作面巷道布置

1.2 物理模型的构建

根据羊场湾矿井Ⅱ020612回采工作面原比例尺寸，及数值模拟平台情况，适当简化部分巷道，建立三维立体模型，如图2所示。根据矿井实际采煤高度及巷道设计情况，将巷道截面简化为宽5 m、高3 m的矩形。

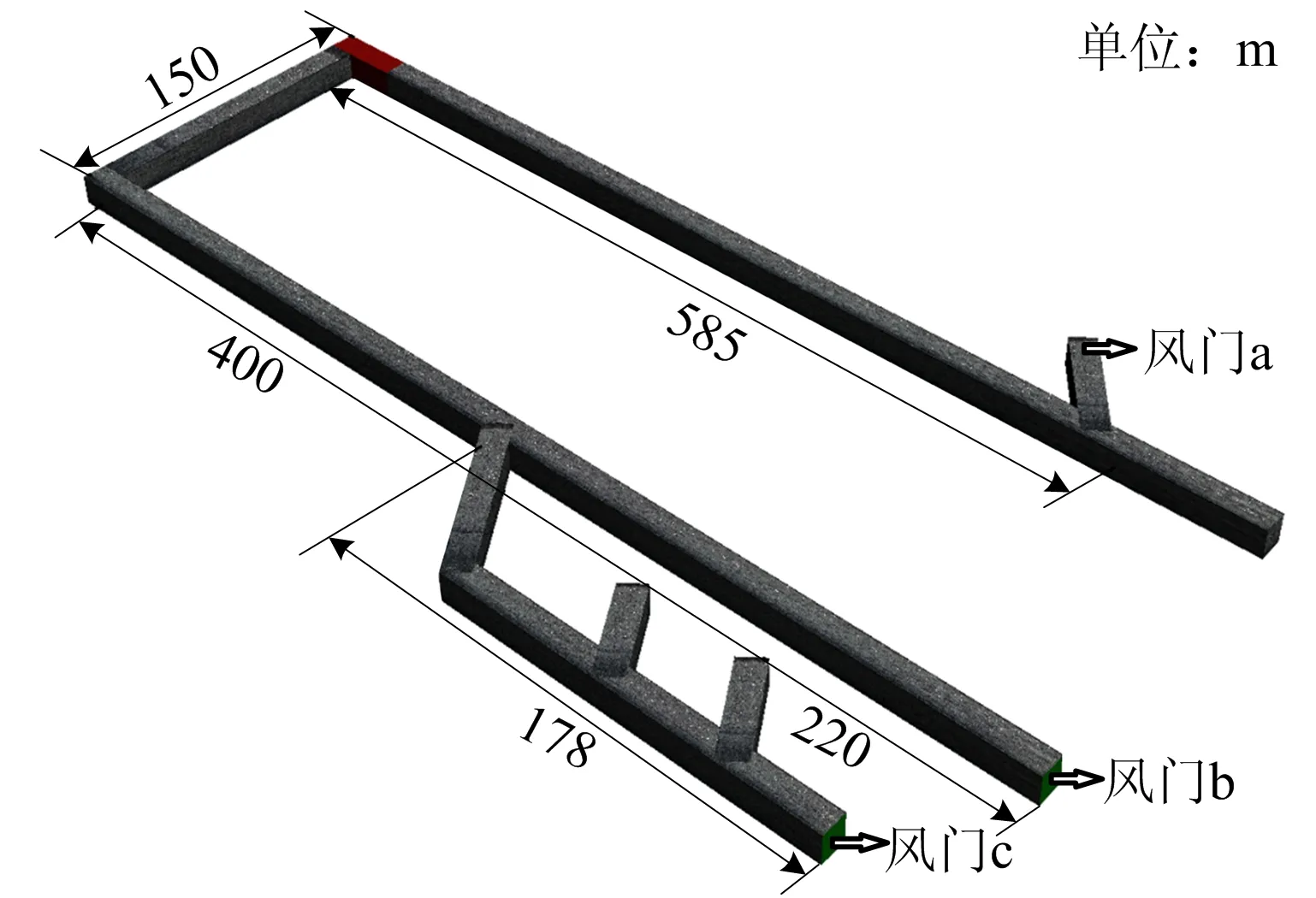
图2 三维几何模型

利用ANSYS软件中mesh单元模块对所建立的三维几何模型进行网格划分。为提高计算效率，采用500 mm划分1个网格。

1.3 数学模型的确定

瓦斯爆炸本质上是带化学反应气体的流动过程，可用Navier-Stokes(N-S)方程来模拟，包括质量守恒方程、能量守恒方程以及描述化学反应的组分方程。具体方程可以统一表示为式(1)：

(1)

式中：ρ为流体的密度，kg/m3；xj为空间坐标(j=1，2，3)；uj为直角坐标系下xj方向的速度分量，m/s；φ为通用变量；t为时间，s；Sφ为源项；Γφ为φ的交换系数。

瓦斯爆炸是1种剧烈的化学反应，瓦斯爆炸后流场会产生较多大漩涡，因使用N-S方程对瓦斯爆炸状况下进行数值模拟时计算量过大，因此本文利用大涡模拟(LES)方法对其进行计算。通过该方法将流场进行划分，按照尺度大小分为大尺度和小尺度，对大尺度的流场通过N-S方程进行直接计算，小尺度流场进行数值模拟。

2 瓦斯爆炸求解参数的确定

2.1 边界条件的设置

1)将采区运人下山、采区轨道下山与回采工作面进风巷支路接触面设为压力入口，采区回风下山与回采工作面回风巷相交的断面设为压力出口。

2)将其他面边界类型均设置为绝热壁面，温度为300 K；壁面无位移与渗透，且与外界无热辐射及热交换。

3)风门在矿井中的主要作用是确保通风系统的稳定，减少无效漏风，通常为关闭状态。在数值模拟中设置风门边界类型为墙壁，将所在断面设置为数据测量点，记录风门的平均超压变化。

2.2 初始条件的设置

结合羊场湾矿井的实际瓦斯涌出情况，设置回采工作面上隅角聚集瓦斯的体积分数为9.5%(空气预混气体)，聚集区域的长度为0.3，2.3，4.3，6.3，8.3，10.3，12.3 m，对应的瓦斯积聚体积为5，35，65，95，125，155，185 m3。

1)充填瓦斯区域(除点火区外)的初始条件：预混气体中各组分的质量分数分别为ωCH4=0.053，ωO2=0.212，ωCO2=0，ωH2O=0；初始温度T=300 K。

2)一般空气区的初始温度T=300 K；气体中各组分的初始质量分数分别为ωCH4=0，ωO2=0.23，ωCO2=0，ωH2O=0。

3)点火区设置为1个球性高温、高压区域，假设氧化反应完全，温度为T=1 600 K；点火区中气体各组分质量分数分别为ωCH4=0，ωO2=0，ωCO2=0.145，ωH2O=0.118。

2.3 求解参数设置

壁面采用标准壁面函数，甲烷燃烧化学反应采用Eddy-Dissipation-Concept(EDC)涡扩散模型。压力项、动量及能量湍流相关量、组分相关量采用二阶迎风格式。离散方程组的耦合解采用SIMPLE算法。

3 模拟结果分析

3.1 风门冲击载荷随时间的变化

为研究瓦斯爆炸后冲击波对风门的影响，模拟上隅角瓦斯积聚体积为5，35，65，95，125，155，185 m3时风门的冲击载荷变化。

瓦斯积聚体积95，125，155，185 m3的情况下各风门冲击载荷随时间的演变过程如图3～5所示。

由图3～5可知，不同瓦斯爆炸体积下风门a～c冲击载荷随时间的演变规律基本均为瞬间达到最大值，之后快速衰减，在短时间内再次上升。

由图3～4可知，风门a～b处冲击载荷随着时间的变化情况基本一致，出现2个峰值，各个峰值形成原因不同。由于瓦斯爆炸后产生具有高温高压的爆轰气体，产生的气体压缩周围的空气，导致空气压强跳跃式升高，空气产生高速位移，形成1个压缩状态的冲击空气层；当压缩的空气层至风门时，风门状态参数改变，冲击载荷突跃，形成第1个冲击载荷峰值。冲击波的波阵面在到达风门后产生反射，风门冲击载荷在峰值后下降，由于冲击波是由多道压缩波叠加形成，波阵面在风门处反射后与后方压缩波相遇，产生碰撞与反射，部分冲击波再次传播至风门处，形成峰值2。冲击波向前推进时，由于受井下巷道壁面限制会向其他方向传播，并在粗糙的巷道壁面上发生反射，巷道形状不同，则反射波大小、方向及到达风门时间不同。因此，风门冲击载荷在恢复到常压过程中有不同程度的波动，在曲线上表现为峰值2后的波动式下降。

图3 风门a在不同瓦斯积聚体积下冲击载荷变化

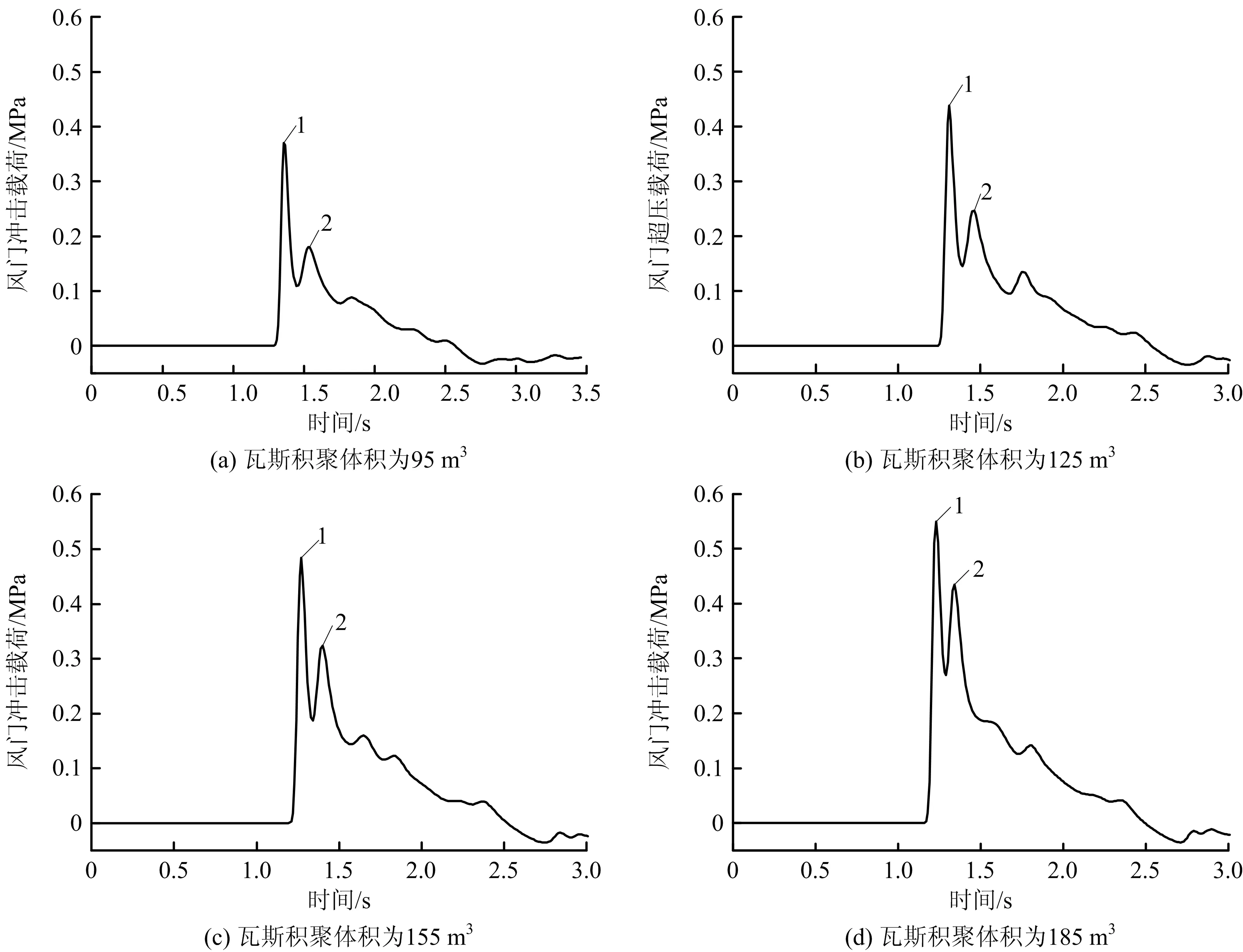
图4 风门b在不同瓦斯积聚体积下冲击载荷变化

由图5可知，风门c冲击载荷变化在前期与风门a～b变化相同，但在后期出现峰值3。这是因为风门c在回采工作面进风巷支路中，风门b在回采工作面进风巷中，冲击波在风门b的表面反射后沿进风巷返回进入支路中，且远大于风门c处的反射波，因此会继续向风门c传播，导致风门c冲击载荷值再次上升，形成峰值3。

图5 风门c在不同瓦斯积聚体积下冲击载荷变化

3.2 不同瓦斯爆炸体积对风门冲击载荷最大值的影响

根据模拟的结果分析不同瓦斯爆炸体积对风门冲击载荷的影响，得出风门冲击载荷最大值随着瓦斯变化的规律。

在不同瓦斯积聚体积下风门冲击载荷最大值情况如图6所示。

由图6可知，随着瓦斯积聚体积的增加，冲击载荷最大值增加幅度由大变小，曲线呈现上凸式。瓦斯爆炸体积从5 m3增加到185 m3，风门a冲击载荷增加4.4倍；风门b冲击载荷增加8倍；风门c冲击载荷增加4.6倍。风门b冲击载荷最大值增加幅度大于风门a，c冲击载荷最大值增加幅度。这是由于瓦斯爆炸体积增加，爆炸后冲击波的速度增大，冲击波进入支路中减少，冲击波衰减程度小。

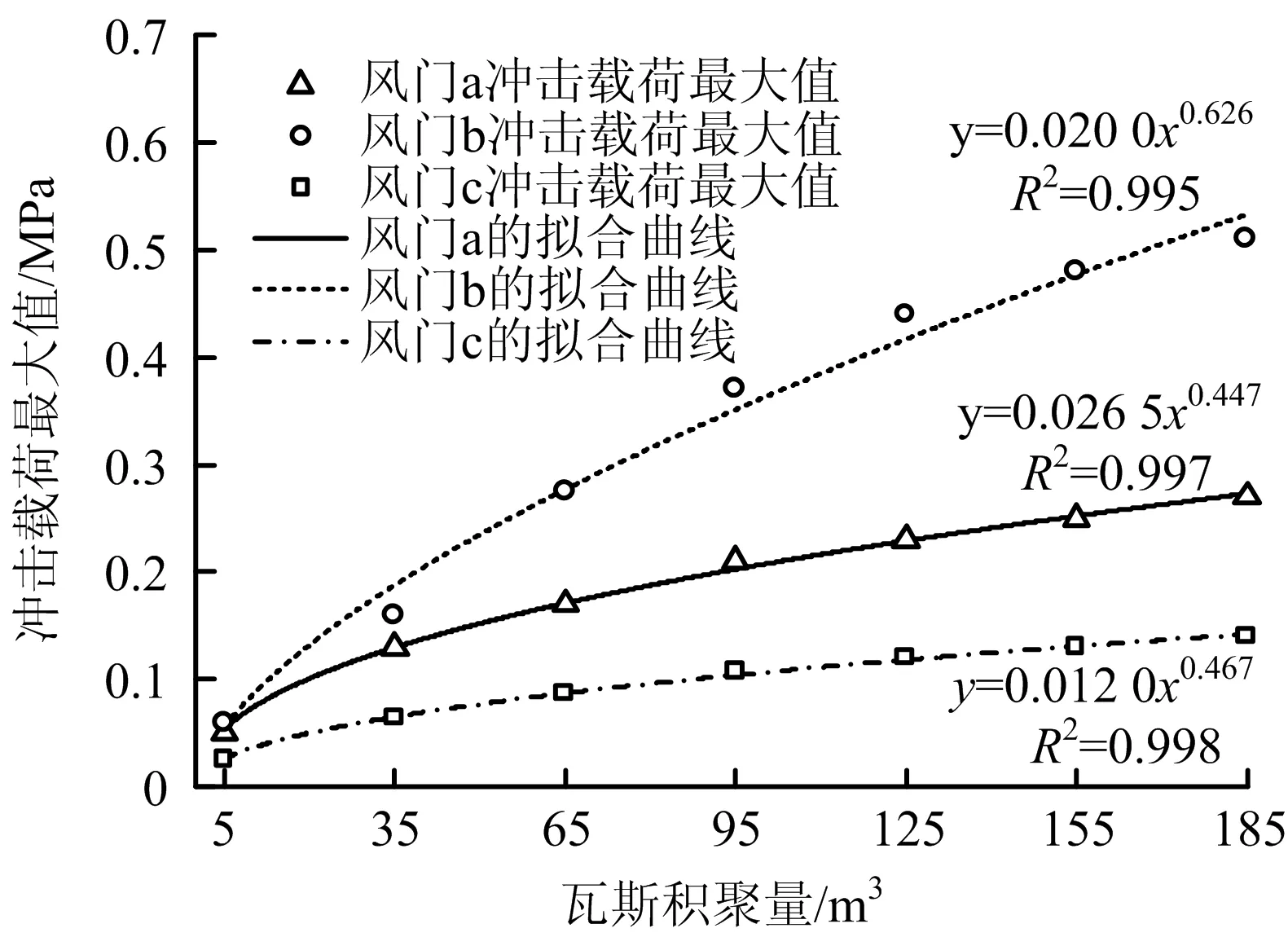
图6 不同瓦斯爆炸体积下风门冲击载荷的最大值

风门冲击载荷最大值与瓦斯积聚量呈现幂函数关系，但不同位置的风门呈现的具体对应关系不同，位于回风巷中的风门冲击载荷与瓦斯积聚体积对应方程为y=0.026 5x0.447，位于进风巷直巷中的风门对应方程为y=0.02x0.626，位于进风巷支巷中的风门对应方程为y=0.012x0.467。

3.3 不同瓦斯爆炸体积对风门冲击载荷达到最大值的时间影响

不同瓦斯爆炸体积下风门到达冲击载荷最大值的时间随瓦解积聚量变化如图7所示。由图7可知，随着瓦斯爆炸体积的增加，风门达到冲击载荷最大值的时间减小幅度变小，曲线呈现下凸式。风门a到达冲击载荷最大值的时间小于风门b～c到达冲击载荷最大值的时间，这是由于风门a～c距爆炸地点分别为617，770，750 m，风门a距离爆炸地点较近。风门b达到冲击载荷最大值小于风门c的，是由于风门b在回采工作进风巷中，风门c在回采工作面进风巷支路中，在距离相差较小的情况下，进风巷中冲击波的速度大于进风巷支路中冲击波速度。

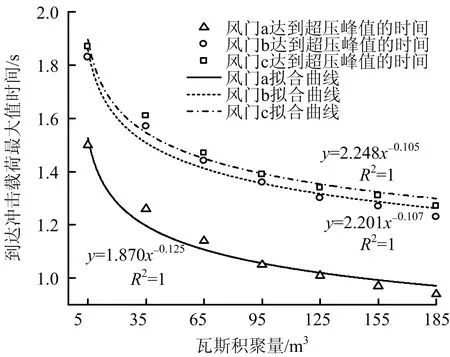
图7 不同瓦斯爆炸体积下风门到达冲击载荷最大值的时间

风门冲击载荷到达最大值时间与瓦斯积聚量呈现幂函数关系，但不同位置的风门呈现的具体对应关系不同，位于回风巷中的到达风门冲击载荷时间与瓦斯积聚量对应方程为y=1.87x-0.125，位于进风巷直巷中的风门对应方程为y=2.201x-0.107，位于进风巷支巷中的风门对应方程为y=2.248x-0.105。

4 结论

1)瓦斯爆炸后，风门冲击载荷出现2次峰值，且第1峰值为最大值；当2处风门设计距离较近时，风门冲击载荷会因另一风门的反射波传播至自身风门处而出现第3次峰值。

2)随着瓦斯体积增加，风门爆炸冲击载荷最大值与瓦斯积聚量呈现幂函数递增的关系，不同位置的风门具体对应关系不同，位于回风巷中的风门冲击载荷与瓦斯积聚量对应方程为y=0.026 5x0.447，位于进风巷直巷中的风门对应方程为y=0.02x0.626，位于进风巷支巷中的风门对应方程为y=0.012x0.467。

3)随着瓦斯体积增加，风门到达爆炸冲击载荷最大值时间与瓦斯积聚量呈现幂函数递减的关系，不同位置的风门呈现的具体对应关系不同，位于回风巷中的达到风门冲击载荷时间与瓦斯积聚量对应方程为y=1.87x-0.125，位于进风巷直巷中的风门对应方程为y=2.201x-0.107，位于进风巷支巷中的风门对应方程为y=2.248x-0.105。