扰动法在风网解算中的应用研究*
2021-06-08赵自豪李鹏慧吕海建
赵自豪,李鹏慧,吕海建
(内蒙古科技大学 矿业与煤炭学院,内蒙古 包头 014010)
0 引言
矿井分风系统解算的本质是解非线性方程组,解算方法可以分为回路分析法和节点分析法2类。回路分析法利用节点风量连续方程和回路风压连续方程构建方程组,在处理进风井和出风井的开口节点时,需要引入虚拟回路的概念[1-2],该方法多用牛顿迭代法进行求解,其难点在于独立回路矩阵的求取、解算结果的初值依赖和如何提高解算效率上;节点分析法利用节点风量连续方程和节点压降方程构建方程组,在处理进风井和出风井的开口节点时,往往引入固定等级节点概念[3-4],该方法多用线性逼近法进行解算,其难点在于如何处理计算结果的摆动收敛问题。
回路分析法按照解算方程组的方法不同,分为牛顿法、斯考特-恒斯雷法、连续法(同伦法)等。牛顿法是目前最常用的风网解算方法,该方法虽然对初值有依赖,但理论上严格收敛,且有唯一解,其缺点是每次迭代都需要重新计算雅克比矩阵的逆矩阵,计算量偏大。文献[5-8]在对雅克比矩阵的对称性进行分析的基础上,提出利用LDLT分解法求解雅克比矩阵的逆矩阵,并用计算机并行运算的方式进行实验验证,结果表明利用LDLT分解法相较于传统解法可节约50%的工作量。斯考特-恒斯雷法是基于在牛顿法不严密假设基础上的1种风网快速解法,该方法较牛顿法计算量小,但容易出现计算结果不收敛的情况。文献[9-11]基于传统的最小生成树原理对斯考特-恒斯雷法进行改进,通过改进的BFS生成树创建法和双通路快速回路圈划法,有效避免斯考特-恒斯雷法的初值依赖问题,加大收敛速度,避免计算结果发散的情况发生。扰动法是在工程和科学计算中常用的1种解析近似方法,该方法基于渐近级数理论,对扰动级数在工程允许的范围内进行截断,从而获得1个近似的表达式,该表达式的解根据截断项的多少,在一定精度内逼近原方程的解。利用该方法,无需执行循环运算,无需设定初值,计算时间可预估,在工程允许的误差范围内,简单有效。Basha等[12]首先在供水网络解算中引入扰动分析法,通过对含多级加压水泵和出水点的复杂水网进行模拟计算,表明在工程允许的精度范围内,该方法相对于传统方法快捷高效;Bush[13]从数学的角度论证扰动法在解算多元二次方程组时的精度问题和收敛问题,从理论上证明该方法解算流体网络的可行性;王树刚等[14]将扰动法的原理应用于流体网络的灵敏度分析问题,提出流体网络中灵敏分支的特征值计算公式和灵敏分支的识别方法,并进行理论验证。
本文在深入研究矿井风网解算传统方法的优缺点及发展趋势的基础上,将扰动法引入风网解算领域;并针对风网解算的特点,演化出扰动法的矩阵表示法,针对3种常见的风机工况点,提出扰动法的扰动方程系数矩阵的构成原理和MATLAB扰动解算法的算法步骤;就扰动法中出现的数学公式定义域问题给出解决办法;通过2个具体实例,验证该方法的可靠性和高效性。
1 通风基本关系式的扰动法表示
扰动法是1种基于级数的近似算法,本文用到的2个级数展开如式(1)~(2)所示:
(1)
(2)
式中:z为扰动法展开式里的1个未知数。
1.1 通风阻力定律的扰动法表示
在不考虑方向性的情况下,通风阻力为正,则反映风量与通风阻力之间关系的通风阻力定律可改写为式(3)[15]:
Q=αhx
(3)
式中:Q为风量,m3/s;h为通风阻力,Pa;α为风量和通风阻力的关系系数;x为常数,取0.5。
α可以用风阻表示,如式(4)所示:
(4)
式中:R为风阻,Pa。
对式(3)利用δ展开,可以获得1个关于变量δ的多项式扰动级数。将h表示为式(5):
h=h0+h1δ+h2δ2+h3δ3+h4δ4+O(δ5),δ=x-1
(5)
式中:δ为用扰动法展开式的变量;h0~h4均为展开式各项的系数;O(δ5)为展开式的余项。
则得式(6):
hx=hhδ=heδlnh
(6)
将式(5)代入lnh,并取前5项,得式(7):
(7)
利用式(1)~(2)和式(5),则式(6)最终展开为δ扰动级数,得式(8):
(8)
则通风阻力定律可表示为式(9):
(9)
1.2 风机特性曲线的扰动展开表达式
对于任意采用机械通风的矿井,至少存在1个风机。风机的风量和风压之间的关系可表示为式(10):
(10)
式中:hp为风机的风压,Pa;Qp为风机的风量,m3/s;p,q,r为各项系数;η为风机效率。
1)若p>0
通过数学变换,式(10)可以表示成式(11):
Qp=ap(hp+cp)x-bp
(11)
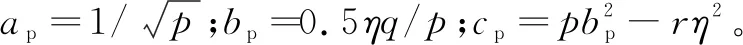
2)若p<0
同理,得式(12):
Qp=ap(-hp+cp)x-bp
(12)

3)若p=0
此时风机特性曲线为1条直线。
类似式(8),风机性能函数方程可展开为式(13):
(13)
2 风网中风流流动的基本定律
在1个分风网络中存在如式(14)所示的关系:
NP=NJ+NL+NF-1
(14)
式中:NP为分支数;NJ为连接节点数;NL为独立回路数;NF为固定等级节点数。
此处,固定等级节点是在水力网络解算时的常用说法,指的是固定水头压力或固定流量的节点。在风网解算中,也就是进风井或出风井的开口节点。为表达简洁仅讨论NF=2的情形。
对于连接节点,满足风量连续方程,如式(15)所示:
BAHx=0
(15)
式中:A=(α)NP×NP为对角线矩阵,对角线上按顺序存储每个分支的α值;B=(b)NJ×NP为连接节点的基本关联矩阵;H=(h)NP×1为分支风压向量[14-15]。
对于独立回路,满足回路风压连续方程,如式(16)所示:
CH=0
(16)
式中:C=(c)NL×NP为仅与连接节点相联分支的独立回路矩阵。
在风网解算中,可以用虚拟回路的方式将固定等级节点转变为连接节点。本文不假设虚拟回路,则有NF-1个通路压降方程或固定等级节点风量连续方程。
常见的3种风机工况下的扰动方程矩阵表达式如下。
1)若风机处于固定风压工况点Hp
根据固定等级节点的分布,选定NF-1个连接2个固定等级节点的独立风路组合,得出通路压降方程,如式(17)所示:
FH=Hp
(17)
式中:F=(f)(NF-1)×NP为通路分支关联方程系数矩阵;Hp=(hp)(NF-1)×1为每个通路对应的总压降。
2)若风机处于固定风量工况点Qp
选定NF-1个固定等级节点,写出针对固定等级节点的风量连续方程,如式(18)所示:
BfAHx=Qp
(18)
式中:Bf=(bf)(NF-1)×NP为固定等级节点的基本关联矩阵;Qp=(qp)(NF-1)×1为对应固定等级节点的出入风量。
3)若给定风机的性能函数
此时需要同时确定风机的风量Qp和风压Hp,相当于增加NF-1个未知量。
①通路压降方程如式(19)所示:
FH-hp=0
(19)
②固定等级节点风量连续方程如式(20)所示:
BfAHx-ap(hp+cp)x=bp
(20)
3 分风网络扰动法的矩阵表示法及求解公式
3.1 固定风压工况分风网络求解
对式(15)~(17)联立方程,得式(21):
(21)
令M,N,P如式(22)所示:
(22)
得式(23):
Mh+N(hx-h)=P
(23)
将式(5),式(8)代入式(23),可得固定风压工况点时的通风网络方程扰动展开式。
根据扰动理论,首先忽略扰动展开式的扰动项,得关于h0的线性方程组,如式(24)所示:
(24)
然后,将h0代入通风方程扰动展开式,且只保留δ扰动项,同时令P=0,得出关于h1的线性方程组,如式(25)所示:
(25)
类似的,可求得h2,h3,h4的解。h2,h3的解如式(26)~(27)所示:
(26)
(27)
式中:h0,h1,h2,h3均为NP×1的列向量,如h0=(hoi)NP×1代表分支1~NP的通风阻力关于h的主扰动项系数。h1~h3分别为1~3次扰动项系数。
从以上各扰动系数的表达式形式来看,除扰动主项外,其他扰动系数括号外的部分均相同,其结果可重复利用。只有括号内的算式部分有差异。但该部分执行的是向量元素之间的代数运算,相比矩阵运算,其复杂度非常小。因此,随着要求计算精度增加,其增加的运算量不明显。
3.2 固定风量工况分风网络求解
联立式(15)~(16),式(18),得式(28):
(28)
记M,N,P如式(29)所示:
(29)
可写出同式(23)形式完全相同的方程式,其求解过程与式(24)~(27)完全相同。
3.3 给定风机性能函数的分风网络求解
假定矿山风机为抽出式通风,对于连接风机的固定等级节点,其风机分支的基本关联系数为1。在风机性能函数p<0时,联立式(12),式(15)~(16),式(19)~(20),得式(30):
(30)

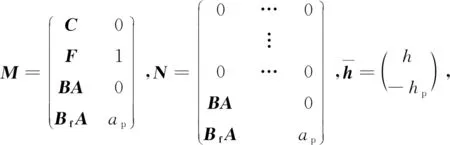
(31)
仿照式(23),可写出给定风机性能函数下的通风网络方程组,如式(32)所示:
(32)

将式(5)、式(8)、式(13)代入式(32),获得通风网络方程扰动展开式。
(33)

(34)

4 扰动法解算通风网络的流程
式(3)成立的基本条件是h>0,但在扰动法解算风网时需要计算lnh0,hx./h0,所以在计算过程中,当h0≤0时,会出现计算错误,从而导致解算失败。下面分别讨论如何处理此种情形。
1)h0<0
在通风网络解算时,基本关联矩阵、独立回路矩阵等的选取依赖于事先假设的分支风流方向。如果事先假设的分支风流方向错误,会出现h<0的情况,进而h0<0。则式(23)~(25)中涉及到计算lnh0时会出现错误,导致计算失败。出现这种情况时,修改原来假设的分支风流方向即可。反应在对应矩阵上,可以在式(22)解算结束后,根据h0的正负,利用代码1更新矩阵M,N,h0。
>>Sig=diag((h0>=0)*2-1);
>>M=M*Sig;N=N*Sig;
>>h0=abs(h0);
代码1
diag函数用来将向量展开为对角线矩阵。Sig为对角矩阵,当h0≥0时,对角线上相应位置为1,否则为-1。
2)h0=0
当风网的拓扑结构和分支参数处于某种特殊状态(如对称状态)时,容易出现某些分支风量为0的情形。此时h=0,根据扰动理论,其所有扰动项系数均为0。在MATLAB中会导致无法计算lnh0,hx./h0,从而使解算失败。这时,可以进行如代码2所示处理,直接令扰动项系数为零,从而跳过对数和除法运算。
>>x0=h0,x0(~~x0)=1./x0(~~x0);
>>y=h0,y(~~y)=log(y(~~y));
代码2
经过以上处理后,则hx./h0转化为hx.×x0,需要计算lnh0的地方,替换为y。
综上所述,利用扰动法解算通风网络的流程如下:
1)分析通风网络图,找出连接节点、独立回路和固定等级节点;
2)对网络中所有的分支,根据R计算出α,写出矩阵A。写出对连接节点、固定等级节点的基本关联矩阵B,Bf。写出对独立回路的独立回路矩阵C和对固定等级节点的通路压降矩阵F。写出Hp,Qp等;
3)根据风机性能函数,计算参数ap,bp,cp;
4)将A,B,Bf,C,F,Hp,Qp,ap,bp,cp等构建矩阵M,N,P,T;
5)计算M的逆矩阵,并求出-M-1N;
8)根据代码2处理后续的牵涉到计算lnh0,hx./h0的公式;

10)根据式(5)求解通风网络各分支的通风阻力,根据式(3)求解各分支的风量。
5 计算实例
5.1 固定风压工况点的计算实例
文献[6]针对通风网络1分风网络利用拟牛顿法和直接解非线性方程法,在MATLAB中进行解算。此处风机工况点固定在500 Pa的风压处。通风网络1如图1所示,其中,1~6表示支路,Ⅰ~Ⅴ表示节点。

图1 通风网络1
为验证扰动法的有效性,根据事先拟定的分支风流流向,遵照风量连续方程和风压连续方程,人为设定各分支风量Qr。指定部分分支风阻,推算出其他各分支风阻和所有分支风压情况。各分支的风阻、风量和风压见表1,单位取标准国际单位。此处的风量为对应风阻情况下的精确解。

表1 通风网络1的相关参数


表2 扰动法和牛顿法解算效果比较
由表2可知,限定的精度下,扰动法的精度相当于牛顿法8次迭代时的精度,且用时远小于牛顿法。随着扰动项指数的增加,扰动法的计算误差以0.5倍的速率递减。但通过分析扰动法的计算原理可知,扰动项指数每增加1,需要计算的扰动项系数的个数增加1倍,理论上其计算时间也会增加。而牛顿法的每次迭代时间是相同的,并且迭代次数10次以内时误差下降速率最大。从本文案例中可以看出,在分支误差控制在1%左右时,扰动法用时远小于牛顿法。
5.2 给定风机性能函数的求解实例


图2 通风网络2
根据分析,该风网有12个分支,6个连接节点,2个固定等级节点,5个独立回路。故M,N均为13×13的矩阵,文献[8]中计算出有2个分支风量为0,本文针对存在0风量分支的风网解算进行说明。

利用牛顿法进行验算,证明用扰动法计算的精度同牛顿法计算20次时的精度相近,且所用时间远小于牛顿法,具体验算过程和产生的数据表格同5.1节类似。
6 结论
1)在扰动法系数求解的过程中,仅需要计算1次风网方程组系数矩阵M的逆,并且除扰动主项系数外,其他扰动项系数的-M-1N部分均相同,可反复利用,而括号内的部分是向量元素间的代数运算,故计算工作量远小于其他传统方法。
2)利用扰动法无需迭代运算,无需进行多次循环运算、判断。并且其矩阵运算量相较于牛顿法的每次迭代都要小,在工程允许的精度范围内,其耗时远小于同精度下的牛顿法。
3)扰动法无需提供计算初值,克服了牛顿法的初值依赖性问题。
4)由于该方法中用到对数计算和除法运算,因此从数学角度讲需要保证h≥0。本文通过增设MATLAB运算代码来修改原来假设的分支风流方向,并对无风分支进行特殊处理,确保计算的成功。
