互联电网的同步及稳定性研究

陈思谕，邹艳丽，傅 杰

（1.玉林师范学院 物理与电信工程学院，广西 玉林 537000；2.广西师范大学 电子工程学院，广西 桂林 541004）

0 引言

随着社会的快速发展，人们对电能的需求日益增加，区域电力资源和负载的不均衡分布［1］，促使电力系统面临区域供电紧张的巨大挑战。为实现区域电力资源互补，将资源优势转变为经济优势，人们通过建立跨区、跨国的互联电网实现远距离电能输送，比如我国的“西电东送”工程就是互联电网建设的典范［2-3］。

为构建高效稳定的跨区域互联电网，学者们在互联电网的经济效益［4］、可用输电能力［5-7］、潮流计算［8-9］、运行风险与控制策略［10-12］、跨区域电力资源规划与设计［13-14］、同步与稳定性［15-17］等方面进行了大量研究。文献［4］提出一种综合考虑互联电网建设和运行的经济效益评估方法，并通过仿真算例得出了电网互联能显著提高电网经济效益的结论。文献［6］基于互联电网的交换边界节点电压与用户有功负载增长量角度，运用潮流计算的方法计算出跨区域互联电网的可用输电能力，但却未考虑电网间电能传输对互联电网同步和稳定性的影响。文献［9］基于多断面控制原理提出适用于大型互联电网的交流计划潮流算法，并通过算例验证了所提算法的有效性。文献［12］基于MPC 算法提出一种互联电网负荷频率控制方法，并在互联电网的参数摄动、负荷扰动造成系统失稳时验证了该方法的有效性。文献［15］基于直流联络线控制提出一种用于互联交流电网频率支援及恢复策略，实验表明该策略可以有效提高互联电网的稳定性。但上述研究均未考虑互联电网间功率交换、电能输送的影响。在互联电网同步与稳定性研究方面，目前已有研究主要集中在各子网自身电能生产与消耗平衡的电网模型［16-17］以及外界扰动造成互联电网失稳时频率稳定控制策略的研究［12］，考虑互联电网间电能传输对电网同步与稳定性影响的研究还比较少。

基于电力网络的类Kuramotom 模型，并考虑互联电网跨区域电能输送的实际情况，从电网间电能传输量和网间连接数角度对互联电网的同步及稳定性进行研究。

1 类Kuramoto相振子模型

采用电力网络的二阶-类Kuramoto 模型对互联电网间电能输送对整体电网性能的影响进行研究。在电力网络研究中，考虑节点动力学特性的类Kuramoto 模型被广泛应用于电力网络的同步与稳定性研究［16-21］。此模型的数学表达如式（1）所示。

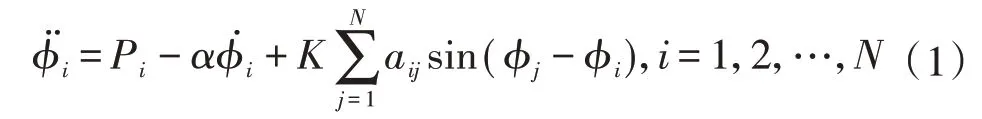
式中：N 为网络节点数；φi为节点i 的相位偏差；和分别为φi的一阶微分和二阶微分，为节点i的频率偏差，用于反映是否恒定不变；Pi为节点i 的功率，当节点i 为发电机时，Pi＞0，表示发电机节点提供功率，当节点K 为负载时，Pi＜0，表示负载节点消耗功率；α 为损耗参数；K 为节点间的耦合强度；｛aij｝为网络的邻接矩阵，描述网络的拓扑结构，本文的研究均在无权无向网络中进行，若节点i 与节点j之间有连边，则aij=aji=1，否则aij=0。

2 电网动力学评价指标

2.1 临界同步耦合强度

在类Kuramoto 模型中，当电力网络节点间的耦合强度K 达到一定强度Kc时，系统经过演化后能够同步运行，此时电网各节点频偏ωi=0；当耦合强度K 小于Kc时，此时电网各节点频偏ωi≠0，系统运行在非同步状态。电网刚好能同步运行的耦合强度Kc称为临界同步耦合强度，Kc越小，表明电力网络的同步能力越好。根据文献［18］的分析，耦合强度K 正比于节点间的最大传输线容量PMAX，因此Kc越小，意味着可以用更小的传输线容量使电网同步运行，降低成本，提高性能；同时，一般电网的同步性能越好，其抗干扰能力越强，电网越稳定。

2.2 最大抗扰强度

在电网稳定性研究中，通常用电网运行在同步状态下，对系统负载施加短暂功率干扰ΔP，在撤除干扰后系统仍能恢复同步运行状态的最大扰动强度ΔPmax来描述电网的稳定性能［16-18］，ΔPmax越大，系统稳定性越好。根据文献［18］的分析以及文献［22］类Kuramoto 动力学模型推导，电力系统能够承受一定的外界干扰，使系统在撤除干扰后能够恢复稳定运行状态，但如果干扰超过一定阈值，则系统在撤除干扰后无法再恢复稳定运行状态。以外界功率为干扰源，研究系统稳定性能，系统可承受的干扰功率越大，则系统稳定性越好。

3 互联电网的拓扑模型构建

在对互联网络进行动力学行为分析之前，须根据真实电网的数据构建便于仿真分析的互联电网拓扑模型。在电力网络研究中，电网的IEEE 标准测试数据是公认的电网数据，其中IEEE14、IEEE30、IEEE39、IEEE57 系统是研究中常用的电网标准网络，各IEEE 标准网络的系统拓扑结构与基本拓扑信息分别如图1和表1所示。

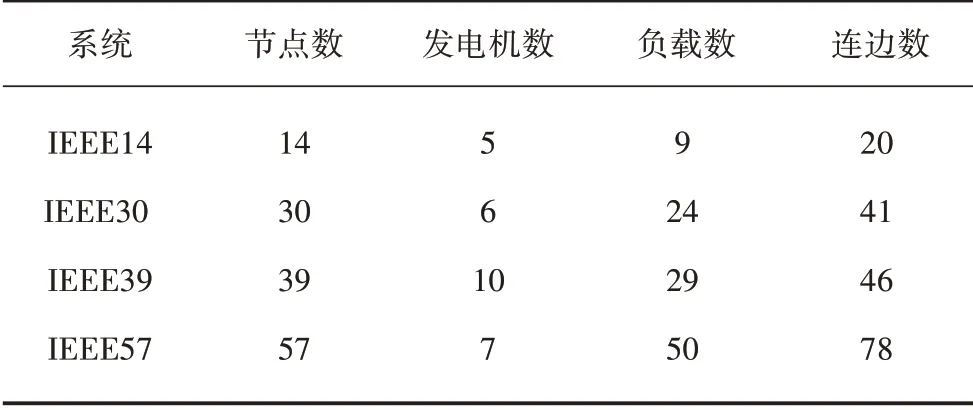
表1 系统基本拓扑信息

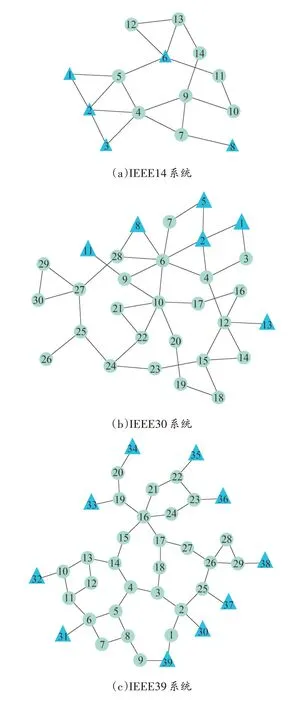
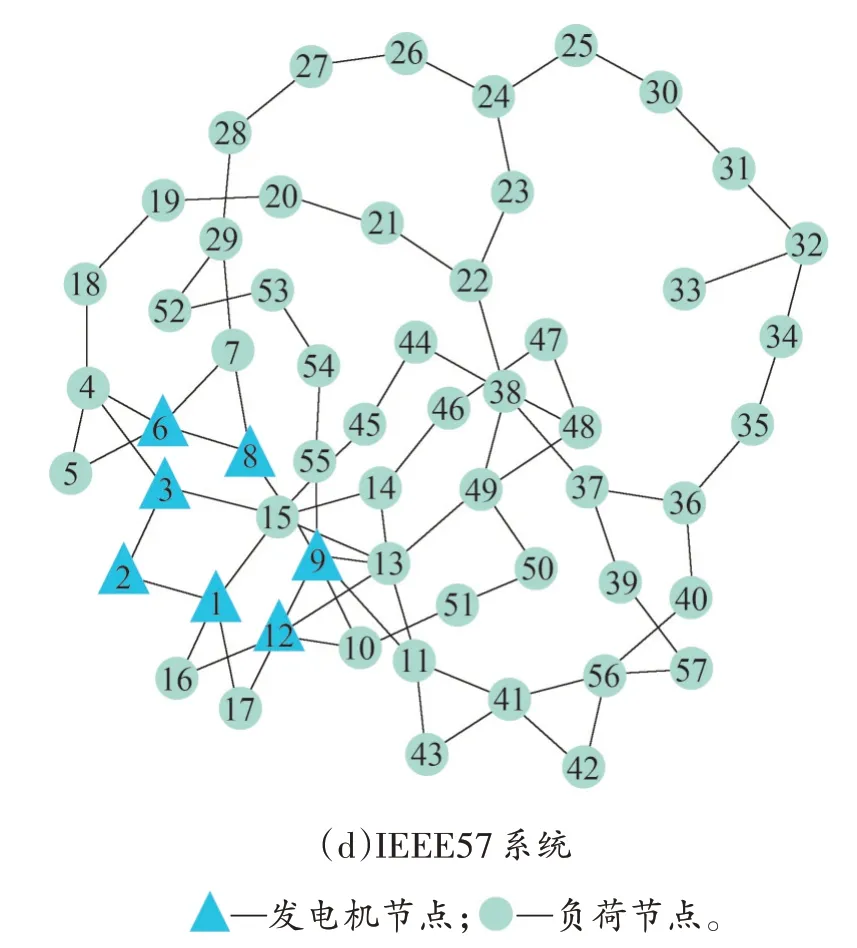
图1 IEEE系统拓扑结构

在 由IEEE14、IEEE30、IEEE39、IEEE57 节 点系统构建的互联电网IEEE14-14、IEEE30-30、IEEE14-39、IEEE30-57 上展开研究工作，其中子网间的连接方式均采用随机连接。当互联电网中两个子网结构不同时，称小子网为子网A，大子网为子网B；当互联电网中两个子网结构相同时，任取其中一个子网为子网A，另一个子网为子网B。当子网A给子网B 提供功率时，电网间输送功率P 取正值，子网B 给子网A 提供功率时，互联电网间输送功率P取负值。令互联电网中负载节点功率Pc=-1，子网A 的负载总功率为PA=-1 × NAc，子网B 的负载总功率为PB=-1 × NBc，子网内发电机功率平均分配，即子网A 发电机功率为PAg=-(PA-P)/NAg，子网B 发电机功率为PBg=-(PB+P)/NBg，其中NAg、NAc分别为子网A 中发电机节点个数和负载节点个数；NBg、NBc分别为子网B 中发电机节点个数和负载节点个数。在仿真分析时，采用经典四阶-龙格库塔积分法进行仿真计算，积分步长h=0.001，损耗参数α=0.1，系统中各节点的初始相位偏差、初始频率偏差均为0。

4 电网间电能输送对电网同步性能的影响

研究互联电网子网间连接数L 一定时，电网间功率传输量对整体电网同步能力的影响，通过互联电网的临界同步耦合强度Kc来描述系统同步性能。令子网间连接数L=5，构建互联电网IEEE14-14、IEEE30-30、IEEE14-39、IEEE30-57，并进行仿真实验。

1）子网结构相同。

在互联电网IEEE14-14、IEEE30-30 上进行仿真，可得子网结构相同的互联电网Kc随电网间传输功率的变化情况如图2 所示，图2 中，子网间连接数取L=5，每个临界同步耦合强度Kc数值均为10 次仿真结果的平均值。

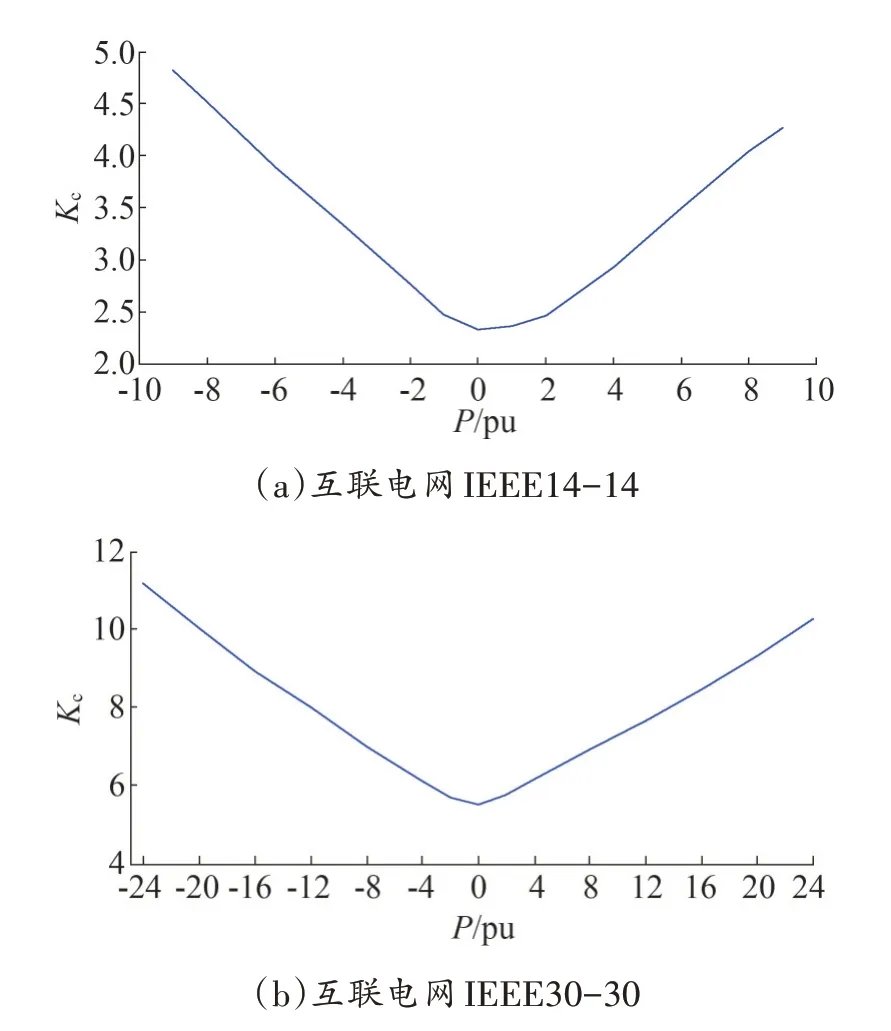
图2 子网结构相同的互联电网Kc随电网间传输功率P的变化情况

由图2 可以看出，结构相同的两个子网构成的互联电网，当两个子网间传输功率为零时，整个电网的同步性能最优，此时两个子网各自平衡功率。当两个子网间有功率输送时，无论子网A 为子网B 供电还是子网B 为子网A 供电，互联电网的同步性能都会恶化，而且两个子网间传输功率越大，互联电网的同步性能恶化越严重。

2）子网结构不同。

在互联电网IEEE14-39、IEEE30-57 上进行仿真，可得子网结构不同的互联电网Kc随电网间传输功率的变化情况如图3 所示，图3 中，子网间连接数取L=5，每个临界同步耦合强度Kc数值均是10 次仿真结果的平均值。

图3 子网结构不同的互联电网Kc随电网间传输功率P的变化情况

由图3 可以看出，结构不同的两个子网构成的互联电网，电网同步性能最优时对应的子网间传输功率不为零，而是一个大于零的正数，记为Pc，电网间传输功率P 偏离最佳网间传输功率Pc时，电网同步性能恶化，偏离的程度越大，电网的同步性能恶化的越严重。在子网间传输功率相同的情况下，如果是小子网A 为大子网B 供电（P＞0），电网同步性能优于大子网B 给小子网A 供电（P＜0）。仿真表明IEEE14-39、IEEE30-57 系统分别在Pc=6、Pc=4 附近临界同步耦合强度取得最小值，系统同步性能最佳，偏离最佳网间传输功率值，系统同步性能恶化。

综上，结构相同子网构成的互联电网，电网间电能的传输降低互联电网的同步性能；结构不同的子网构成的互联电网，小子网A 给大子网B 传输适量电能有利于提高电网同步性能，但电能传输量P 偏离最佳传输量Pc时，将会降低系统同步性能。

5 电网间电能输送对系统稳定性能的影响

研究子网间连接数一定时，电网间功率传输量P 对整体电网稳定性的影响，采用系统最大抗扰强度ΔPmax来衡量。在互联电网IEEE14-14、IEEE30-30、IEEE14-39、IEEE30-57进行仿真，令电网间连接数L=5，构建相应互联电网模型。

1）子网结构相同。

在互联电网IEEE14-14、IEEE30-30 上进行仿真，令IEEE14-14、IEEE30-30系统耦合强度分别为：K=6、K=15，子网间连接数均取L=5，使各系统运行在同步状态，给系统中每个负载节点施加扰动功率ΔP，扰动时间Δt=5 s，系统最大抗扰强度ΔPmax数值取10次仿真结果的平均值，结果如图4所示。

图4 子网结构相同的互联电网的最大抗扰强度ΔPmax随电网间传输功率P的变化

由图4可以看出，由结构相同的两个子网构成的互联电网，在互联电网间的传输功率P 由PA到-PB的变化过程中，互联电网的最大抗扰强度ΔPmax先增大后减小，并均在P=0 处取得最大值，系统抗扰性能最佳，即由结构相同的两个子网构成的互联电网，电网间输送电能将降低系统稳定性。图3 中图形关于P=0 不对称是由于网间连接是随机互联，所得邻接矩阵并不对称，因此电网间功率正负向传输的效果并不相同。

2）子网结构不同。

在互联电网IEEE14-39、IEEE30-57 上进行仿真，令IEEE14-39、IEEE30-57系统耦合强度分别为：K=14、K=23，子网间连接数均取L=5，使各系统运行在同步状态，给系统中每个负载节点施加扰动功率ΔP，扰动时间Δt=5 s，系统最大抗扰强度ΔPmax数值取10次仿真结果的平均值，结果如图5所示。

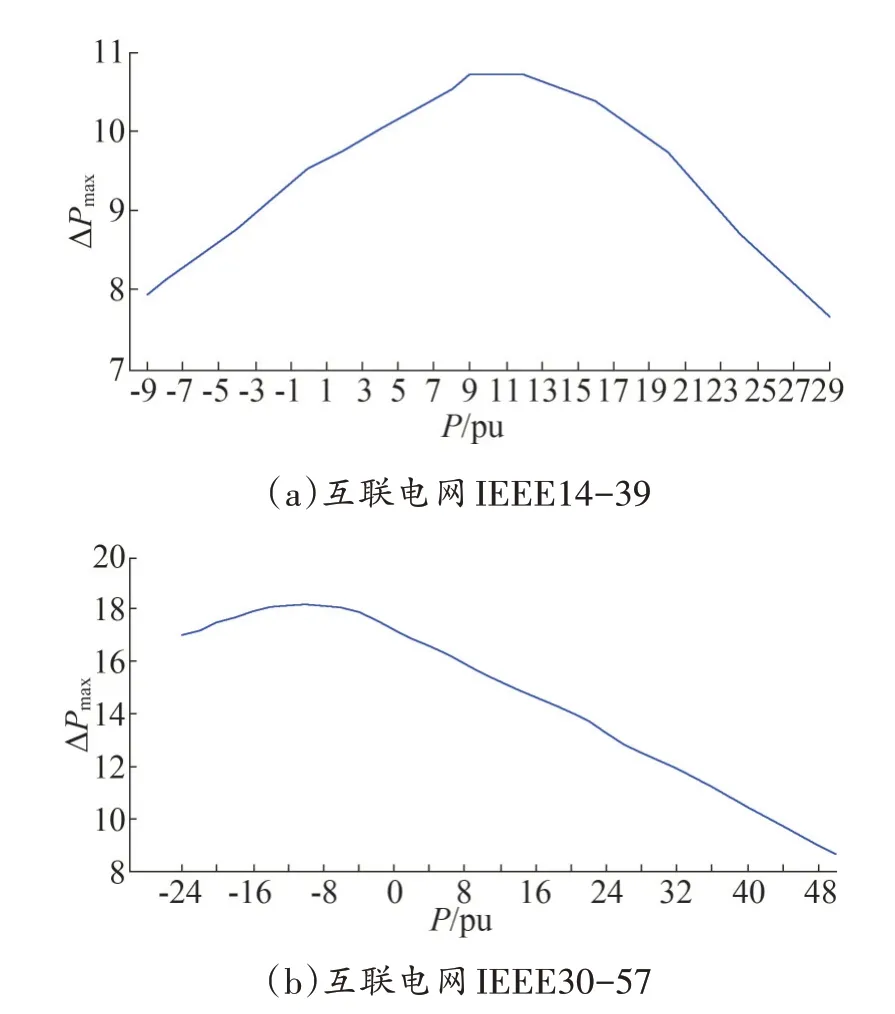
图5 子网结构不同的互联电网ΔPmax随电网间传输功率P的变化情况

由图5 可以看出，结构不同的两个子网构成的互联电网，在互联电网的传输功率P 由PA到-PB的变化过程中，互联电网的最大抗扰强度ΔPmax先增大后减小，在IEEE14-39 系统中，ΔPmax并非在系统最佳同步点P=6 时获得最大值，而是在P=9 处取得最大值，此时系统抗扰性能最佳；在IEEE30-57 系统中，ΔPmax并非在系统最佳同步点P=4时获得最大值，而是在P=-10处取得最大值，此时系统抗扰性能最佳。因此，在子网结构不同的互联电网中，在电网间电能传输最佳稳定点上没有一致性规律。

6 子网间连接数对互联电网同步性能的影响

研究当电网间输送功率P 一定时，子网间连接数对互联电网同步性能的影响，通过互联电网的临界同步耦合强度Kc来描述系统同步性能，仿真结果Kc值均为10次仿真结果的平均值。

1）子网结构相同。

在互联电网IEEE14-14、IEEE30-30上进行仿真，其中IEEE14-14系统电网间传输功率取P=4，IEEE30-30系统电网间传输功率取P=6，仿真结果如图6所示。

从图6 可以看出，在由结构相同子网构成的互联电网中，当电网间传输功率P 一定时，随着子网间连接数的增加，互联电网的临界同步耦合强度Kc先迅速减小，随后波动减小，且减小趋势减缓。

图6 子网结构相同的互联电网临界同步耦合强Kc随子网间连接数L的变化

2）子网结构不同。

在互联电网IEEE14-39、IEEE30-57 上进行仿真，其中IEEE14—39 系统电网间传输功率取P=4，IEEE30-57 系统电网间传输功率取P=8。仿真结果如图7所示。

从图7 可以看出，在由结构不同子网构成的互联电网中，当电网间传输功率P 一定时，随着子网间连接数的增加，互联电网的临界同步耦合强度Kc先迅速减小，随后波动减小，且减小趋势减缓。

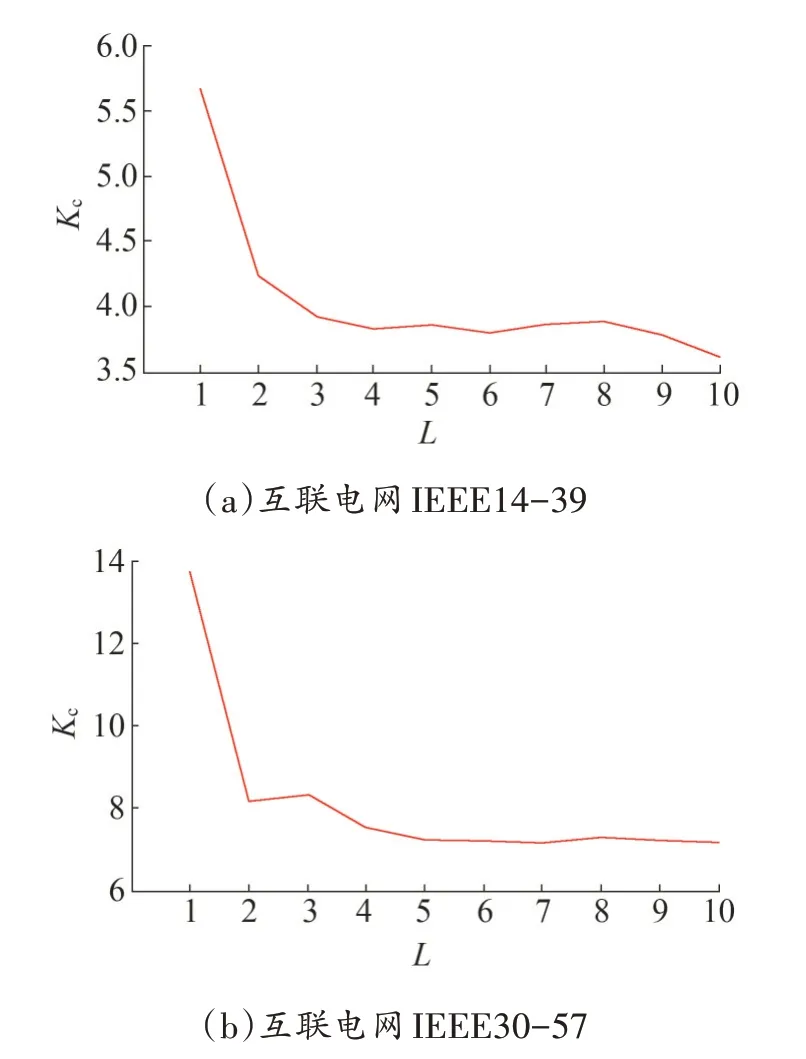
图7 子网结构不同的互联电网临界同步耦合强Kc随子网间连接数L的变化

综上，无论构成互联电网的子网结构是否相同，当电网间传输功率P一定时，当子网间连接数从1条增加为2 条时，系统临界同步耦合强度Kc显著减小，电网的同步能力显著增强；继续增加子网间连接数，Kc波动下降，网络的同步能力虽有改善但不再明显。

7 子网间连接数对互联电网稳定性能的影响

研究当电网间输送功率P一定时，子网间连接数对互联电网稳定性的影响，采用系统稳定状态下可承受的最大功率扰动强度ΔPmax来衡量互联电网的稳定性能，仿真结果ΔPmax值均为10次仿真结果的平均值。

1）子网结构相同。

在IEEE14-14、IEEE30-30上进行仿真，子网间连接方式采用随机连接。在仿真实验中，IEEE14-14系统电网间传输功率取P=4，耦合强度取K=8；IEEE30-30 系统子网间传输功率取P=6，耦合强度取K=12，使各系统运行在同步状态，给每个负载节点施加扰动功率ΔP，扰动时间Δt=5s，仿真结果如图8所示。

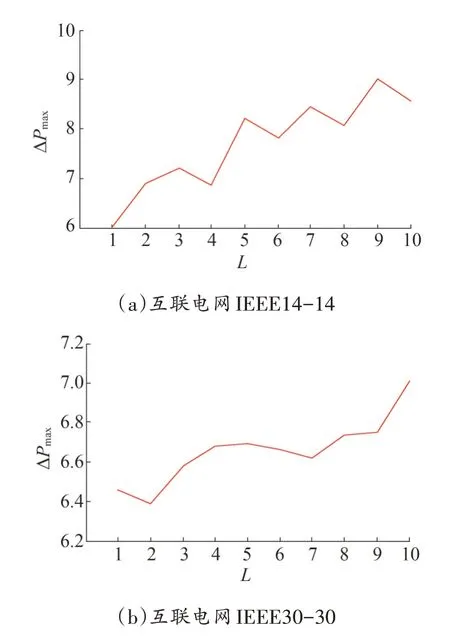
图8 子网结构相同的互联电网的最大抗扰强度ΔPmax随子网间连接数L的变化

由图8 可以看出，在由结构相同子网构成的互联电网中，当电网间传输功率P 一定时，互联电网可承受的最大抗扰强度ΔPmax随着电网间连接数L的增加而呈波动增大趋势，表明在电网间传输功率一定时，随着电网间连接数的增加，系统稳定性呈波动增强趋势。

2）子网结构不同。

在互联电网IEEE14-39、IEEE30-57上进行实验仿真。在仿真实验中，IEEE14-39 系统电网间传输功率取P=4，耦合强度取K=8；IEEE30-57 系统电网间传输功率取P=8，耦合强度取K=18，使各系统运行在同步状态，给每个负载节点施加扰动功率ΔP，扰动时间Δt=5 s，仿真结果如图9所示。

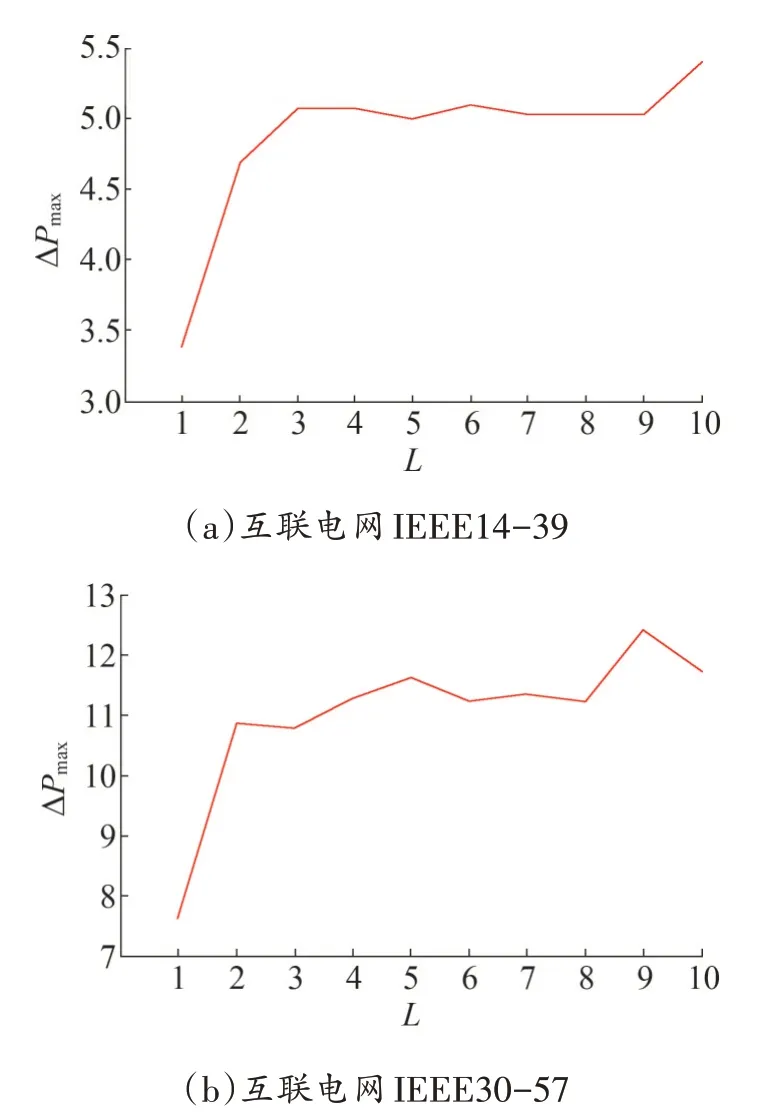
图9 子网结构不同的互联电网最大抗扰强度ΔPmax随子网间连接数L的变化

由图9 可以看出，在由结构不同子网构成的互联电网中，在电网间传输功率P 一定时，当子网间连接数从1 条变为2 条时，电网的抗扰能力有显著增强，此后随着子网间连接数的增大，电网抗扰能力虽有增强，但变化幅度不大。

综上，无论构成互联电网的子网结构是否相同，当电网间传输功率P 一定时，随着子网间连接数的增加，互联电网可承受的最大抗扰强度ΔPmax随着电网间连接数L 的增加而呈波动增大趋势。因此，在电网间传输功率P 一定时，随着电网间连接数的增加，系统稳定性呈波动增强趋势。

8 结语

区域电网进行互联，互相进行电能补充，是提高资源利用率和设备利用率的有效方法。采用IEEE标准测试网络模拟区域电网互联，对互联电网电能输送情况下电力网络的同步及稳定性问题进行了深入的分析研究。研究表明，当子网间连接数一定时，结构相同的两个子网互联，电网的同步能力与稳定性随着电网间传输功率的增大而恶化。结构不同的两个子网互联，当小子网向大子网传输一定功率时，电网的同步能力达到最优，继续增大子网间传输功率值会恶化网络的同步能力。当电网间传输功率一定时，子网间连接数从1 条变为2 条时，对电网同步能力和稳定性的改善最大，继续增大子网间连接数，电网同步能力及稳定性虽有提高但变化不大。