高压直流系统电缆接头中空间电荷与电场分布的仿真计算

吴 洋，朱庆东，高 路，吴 锴

（1.西安交通大学电气工程学院，陕西 西安 710049；2.国网山东电力公司电力科学研究院，山东 济南 250003）

0 引言

随着高压直流输电技术的发展，交联聚乙烯（Cross⁃linked Polyethylene，XLPE）电缆由于其优良的性能正得到越来越广泛的应用［1-2］。在直流高压下，在XLPE的内部容易形成空间电荷的积聚，这些空间电荷会导致XLPE中的电场强度分布发生畸变，最终会导致电缆的击穿［3-5］。

电缆接头是电力电缆的重要组成部分［6-7］，在电缆接头中存在两种不同的绝缘材料，分别是电缆主绝缘使用的XLPE 和增强绝缘使用的乙丙橡胶（Ethylene Propylene Rubber，EPR）。由于两种材料的相对介电常数、电导率、电荷输运参数的不同，在两种材料的界面上会产生空间电荷的积聚，进一步加剧电缆接头中的电场畸变［8］。

高压直流电缆接头复杂的结构与界面情况，使其成为电缆系统中的薄弱点，需要重点研究。受限于现有的空间电荷测量技术，对电缆接头中空间电荷分布情况无法直接进行测量。

近年来，国内外的学者在空间电荷仿真领域展开了一系列的研究。Alison 和Hill 在1994 年首次提出采用电荷输运模型计算研究聚合物介质材料的空间电荷积聚特性［9］，他们考虑了电极-介质界面的电荷注入、电极-介质界面的无阻挡电荷抽出、定常载流子迁移率和单一能级陷阱的捕获，没有考虑陷阱电荷的脱陷，初步得到了交联聚乙烯内部的空间电荷积聚特性。Roy 使用恒定迁移率的流体模型开发了一种数值模型，用于解释聚乙烯中的电荷传输，包括入陷和复合的影响［10］。西安交通大学吴锴课题组采用有限差分法求解电荷连续性方程和泊松方程，研究了试样厚度对介质材料空间电荷积聚的影响［11］。

但是，以往的研究中，空间电荷的仿真为一维简单模型的仿真，主要目的为研究空间电荷输运机理，难以应用到实际工程模型中，为了研究高压直流电缆接头中空间电荷与电场强度分布情况，建立三维的电缆接头仿真模型。

1 仿真理论

绝缘材料中的空间电荷积聚包含一系列复杂的过程，如载流子的注入、抽出、迁移、复合等。空间电荷的分布会影响材料中电场强度的分布，而电场强度的分布也会进一步影响空间电荷在材料中的输运过程。这些过程相互影响，非常复杂。为实现空间电荷的仿真，对一些过程进行了合理的忽略。

1.1 双极性载流子输运模型

采用文献［12］所示的基于抽出受限的双极性载流子输运模型，如图1 所示。空穴从正极注入，从负极抽出；电子从负极注入、正极抽出。在介质内部，电子与空穴在电场的用下进行迁移，并发生正负载流子的复合等过程。

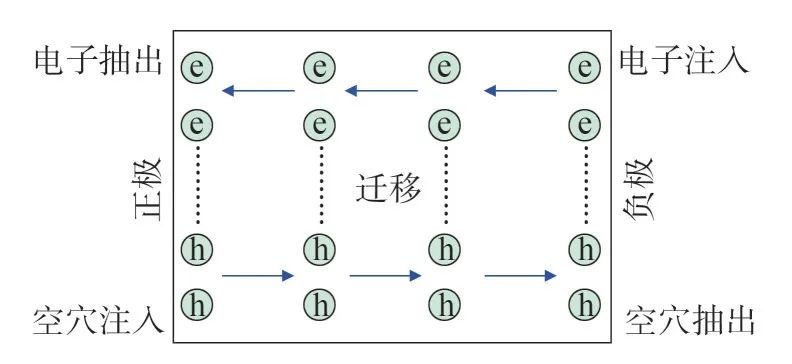
图1 双极性载流子输运模型

通过3 个方程对载流子的输运过程进行描述，如式（1）—式（3）所示。式（1）为输运方程，式（2）为连续性方程，式（3）为泊松方程。

大量实验证明，加速度噪声实际上与物体的加速度有关，只有减小滑块在变形结束时速度突变或延长速度变化所需的时间，才有可能减小加速度噪声。此时，阻尼、隔震等噪声控制技术均无力降噪。正因为如此，当在大型机械压力机上完成冲裁、落料及剪切工艺时，加速度噪声值最高，而在完成模锻、拉深、挤压等工艺时，在滑块到下死点后，由于变形工件的弹性回复力，使回程初期滑块上仍承受力的作用，而这一弹性力是逐渐减小到趋向于零，大大降低了滑块速度变化梯度，所以加速度噪声明显下降。

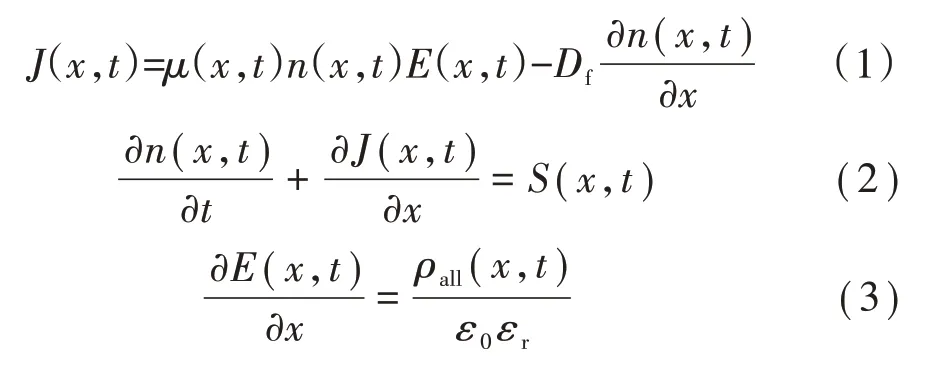
式中：x为位置变量；t为时间变量；J为载流子的通量密度；μ 为载流子的迁移率；n 为载流子密度；E 为电场强度；Df为扩散系数；S 为源项；ρall为总的电荷密度；εr为相对介电常数；ε0为真空介电常数。

使用的载流子迁移率是根据不同场强、不同温度下的电导测量数据得到的，最终结果与温度、场强有关，如式（4）所示。

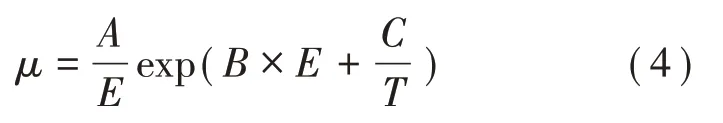
式中：A、B、C为拟合系数；T为温度。

载流子的注入过程遵循肖特基注入原理，如式（5）和式（6）所示。

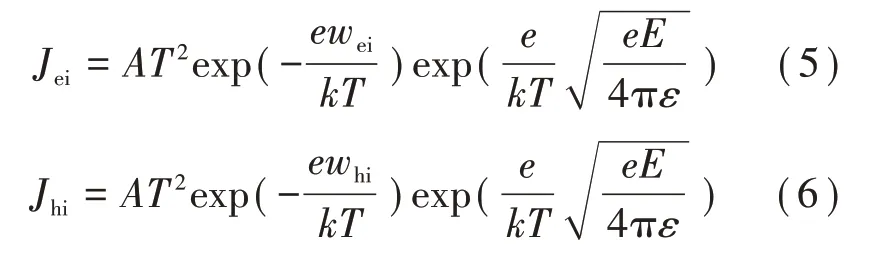
式中：Jhi和Jei分别为在阳极和阴极处注入的通量密度；ωei和ωhi分别为电子和空穴的肖特基注入势垒；e为电子电量；k为玻尔兹曼常数；ε为介电常数。

对于载流子的抽出过程，采用了认为设置抽出系数的方式，如式（7）和式（8）所示。

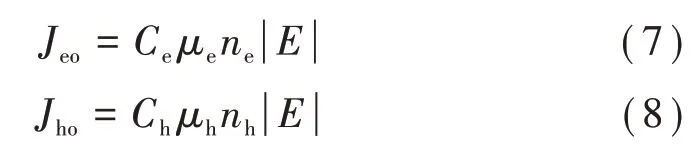
式中：Jho和Jeo分别为空穴在阴极和电子在阳极的抽出通量密度；Ch和Ce分别为空穴和电子在电极处的抽出率，用以近似描述抽出受限；μh和μe分别为空穴迁移率和电子迁移率；nh和ne分别为空穴密度和电子密度。

另外，在电缆的实际运行过程中，由于线芯中电流的作用，线芯的温度会升高，而电缆的外侧由于环境的作用，会保持较低的温度，这就会在绝缘内外形成一个温度梯度。在仿真中，温度梯度的存在也需要纳入考虑。

1.2 仿真模型

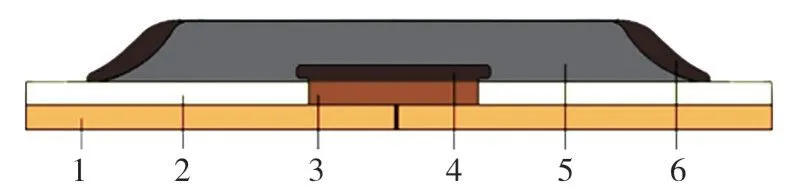
图2 电缆接头模型

在本模型中，应力锥和高压屏蔽均采用半导体材料，而压接管为金属材料，而且该中电缆接头为轴对称结构，仿真模型可简化为如图3 所示的二维轴对称模型，字母a—h代表电缆接头上不同的位置。

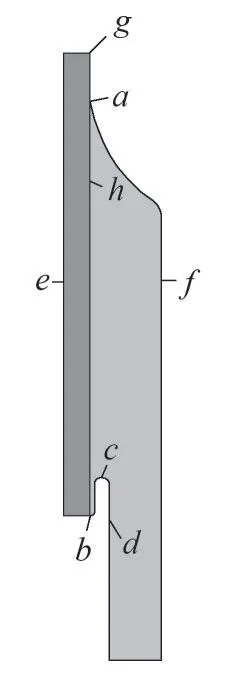
图3 简化的电缆接头模型

表1 为进行空间电荷仿真时使用的部分参数。所采用的电缆接头外表面温度为293.15 K，线芯处施加250 kV直流电压。

表1 仿真参数

2 结果和讨论

2.1 模型验证

为了验证前文所述仿真模型的有效性，首先建立了一个简单的一维模型。利用COMSOL 软件，根据双极性载流子输运模型对一维模型进行了空间电荷仿真，其空间电荷分布如图4 所示，电场分布结果如图5所示。

由图4 可见，在一维模型两侧电极附近，存在异极性空间电荷积聚现象，这是由抽出受限造成的，在异极性电荷积聚的作用下，其电场分布也发生畸变，如图5 所示，两端电极处的电场增大，该结果与实验结果规律相同，说明该模型可以实现空间电荷与电场分布的仿真，是有效的。

图4 一维模型中空间电荷分布

图5 一维模型中电场分布

2.2 电缆接头的仿真

使用前文介绍的简化高压直流电缆接头模型，基于双极性载流子输运模型，利用COMSOL 仿真软件，进行高压直流电缆接头的空间电荷与电场强度仿真，其电场强度的三维仿真结果如图6所示。

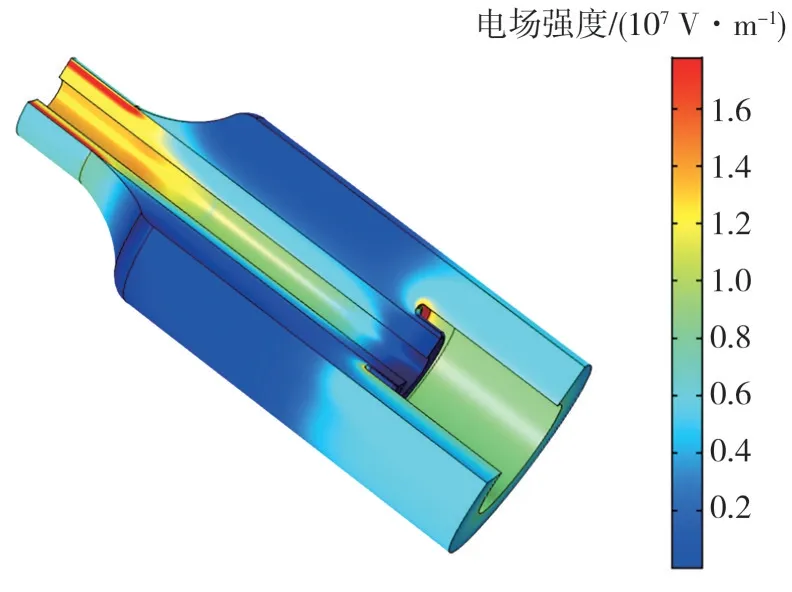
图6 电缆接头电场强度三维仿真结果

沿着轴线做截面，其仿真结果如图7所示。

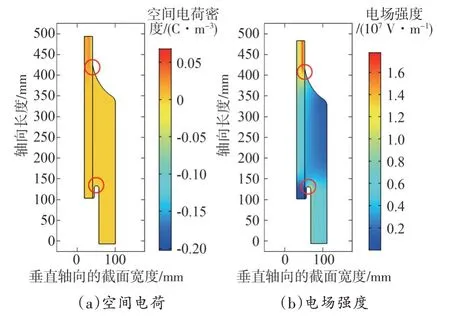
图7 电缆接头中空间电荷与电场分布

从图7 可以看出，在高压直流电缆接头的应力锥根部和高压屏蔽的顶端，出现了严重的电场畸变。

为了更加清楚地观察，对应力锥根部和高压屏蔽的顶端附近空间电荷和电场强度分布进行了局部放大，如图8所示。

由图8 可以看出，在应力锥的根部和高压屏蔽的顶端，出现了异极性电荷的积聚，从而导致了这两个部位出现严重的电场畸变，成为电缆接头中的薄弱点。

图8 应力锥根部和高压屏蔽的顶端附近空间电荷与电场强度分布

高压直流电缆接头中的电场强度最大值出现在高压屏蔽的顶端，将此处附近（图3 中b、c、d 连线）的电场强度提取出来，如图9 所示，可见最大场强达到1.48×107V/m，远大于3.3×106V/m的平均场强值。

图9 高压屏蔽顶端附近电场分布

2.3 界面电荷

电缆接头中存在两种不同的绝缘材料，XLPE 和EPR，在两种材料的界面上，容易出现电荷的积聚现象。

为了观察电缆接头中的界面电荷，建立了一条穿过XLPE 和EPR 的截线（图3 中e—f），这条截线上的空间电荷如图10所示。

从图10 中可以看出，在两种材料的界面处，发生了空间电荷的积聚。这是由于两种材料的载流子迁移率不同，且两种材料之间存在势垒，迁移到此处的电荷不能完全被迁移走，造成了空间电荷的积聚。

2.4 温度梯度的影响

电缆接头负荷运行中，线芯发热使得电缆接头线芯处与电缆接头外侧存在温度差，温度在电缆接头中呈梯度分布。而温度的变化将影响电缆接头中空间电荷的输运过程［13-15］。

设定电缆接头外层的温度恒定为293.15 K。图11 显示了内外温梯为70 K 时，电缆接头中的温度分布情况。

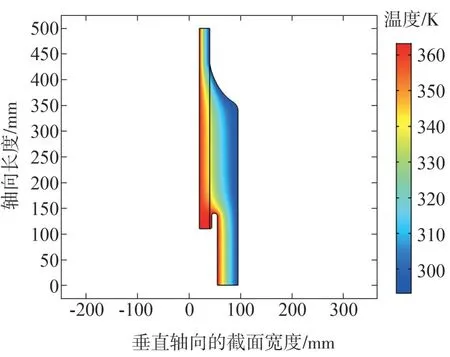
图11 温度梯度为70 K时的温度分布

将高压屏蔽顶端附近的电场强度分布作为研究对象，其在不同温度梯度下的电场强度分布如图12所示。

图12 不同温梯下高压屏蔽顶端附近的电场强度分布

由图12 可以看出，随着温度梯度的提高，高压屏蔽顶端附近的电场强度畸变愈发严重。最大值从温梯为0时的7.9×106V/m增加到了温梯为70 K时的1.48×107V/m。

若根据按照传统的电场计算方法，仅考虑电导率而不考虑空间电荷的仿真模型［16］，高压屏蔽顶端附近的电场强度结果如图13所示。

从图13可以看出，随着温度梯度的增加，该处的电场强度反而减少。这是由于在该模型中，电导率是随温度升高而增加的，而高压屏蔽顶端附近属于高温侧，温度升高，电导率增大，此处的场强也相应减少。

图13 仅考虑电导时不同温梯下的电场分布

造成两种方法之间差异的主要因素，是因为在电导模型中，电荷注入的因素没有考虑在内。实际情况中，温度的升高将大大增强电荷的注入，这些电荷的存在将增大电缆接头中的电场畸变，使用电荷模型更能够清楚地反映这一过程。

3 结语

基于双极性载流子输运模型，利用COMSOL 仿真软件，构建了高压直流电缆接头的仿真模型。根据仿真结果，空间电荷容易累积在应力锥的根部和高压屏蔽层的末端。高压直流电缆接头中的最大电场强度出现在高压屏蔽层的末端，远高于平均电场强度。此外，温度梯度的存在会使电缆接头中的电场失真更加严重。与仅考虑电导率的传统方法相比，该方法可以准确反映由于载流子注入、抽出和迁移所引起的电场畸变。

仿真方法和结果为高压直流电缆接头的设计与优化提供了依据，在设计与制造高压直流电缆接头时，应重点关注应力锥的根部和高压屏蔽的顶端，通过增加曲率半径、增加过渡非线性材料等方式，降低电场畸变程度。