基于结构应力法的焊缝错边疲劳性能分析

2021-06-07赵秋黄冠铭王苹郭杨斌

铁道建筑 2021年5期

赵秋黄冠铭王苹郭杨斌

1.福州大学土木工程学院，福州 350108；2.哈尔滨工业大学先进焊接与连接国家重点实验室，哈尔滨 150001

焊接作为一种连接技术，具有操作灵活、致密性好、成本较低等优点，被广泛应用于工业领域，尤其在钢桥领域应用比较普遍［1］。钢桥中的钢箱梁桥在工厂制造和现场拼装过程中均涉及焊接。受现场环境和施工操作条件制约，在拼装时局部对接焊缝构造较易产生错边（图1）。

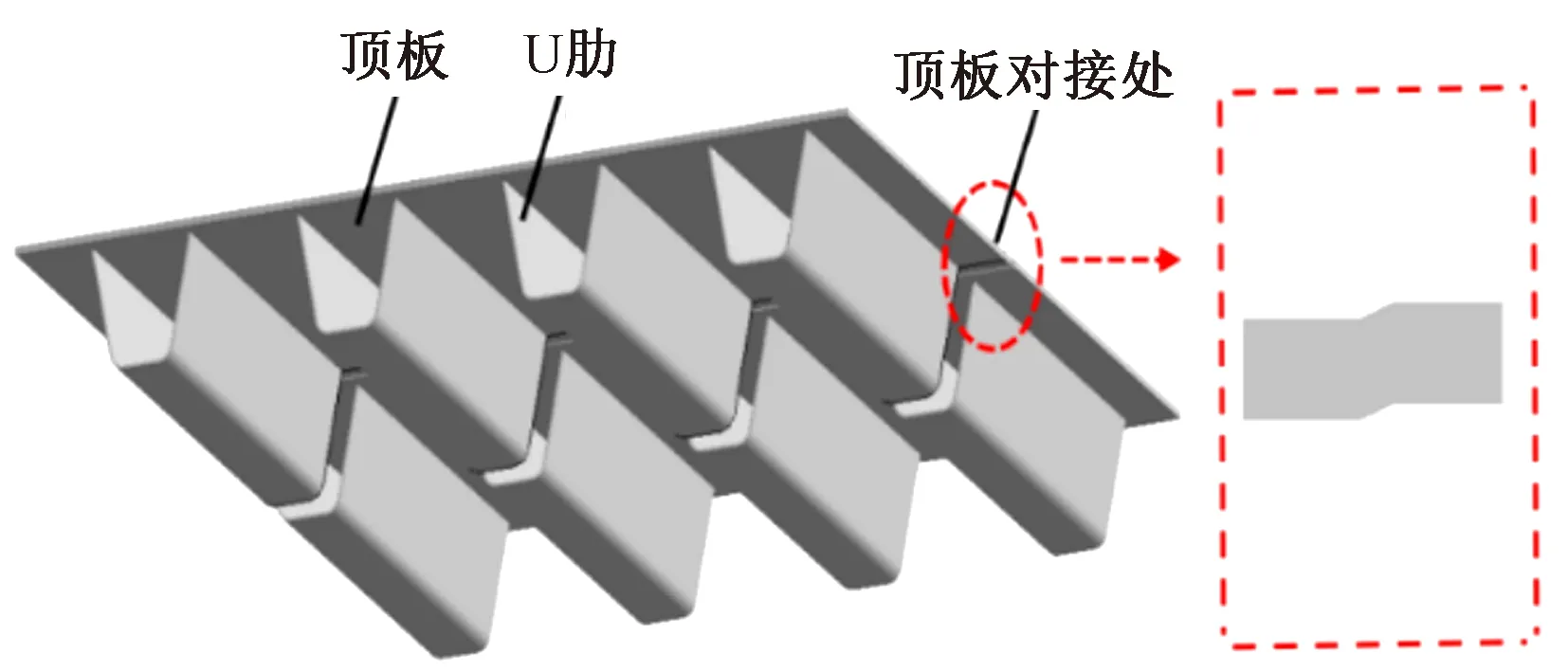
图1 钢箱梁顶板对接处焊缝错边

错边是焊接工程中常见的制造缺陷，即两个焊件表面应平行对齐时未达到规范要求而产生的偏差，包括板材的错边及管材的错边等［2］。错边会导致焊缝附近出现应力集中现象，促使并加快疲劳裂纹的萌生和扩展，进而降低焊接件的疲劳强度和疲劳寿命。文献［3-7］针对各类焊缝错边的成因及其对力学性能的影响等方面进行了研究，发现错边形成的原因较为复杂，受焊接件的组装工艺、焊接环境、人员素质、装配机具等因素的影响。在焊接前母材的组对和定位过程中，不可避免地会形成位移误差，进而导致错边的产生。基于当前制造工艺水平，若追求过高的装配对接精度会极大增加生产成本。综合考虑经济性和安全性，焊缝错边这一缺陷在较长一段时间内难以规避。现有规范对错边量规定了容许范围，但在该范围内错边对焊接件疲劳性能的具体影响仍待研究。在个别结构中，错边量已超过规范限值，如果采用返厂修复或全部更换等处理方式，将面临浪费材料、施工工期不允许等方面的考验。因此，研究错边量对焊接件疲劳性能指标的影响，评估焊缝处理后的疲劳性能并探究高效合理的错边处理方法，对实际工程应用具有极为重要的指导意义。

已有文献分析错边对结构力学性能的影响时均采用名义应力法或热点应力法对构件的工作应力进行计算。但名义应力方法无法体现错边量对计算工作应力和疲劳寿命的影响；热点应力法应用有限元分析工作应力时对网格较为敏感，无法准确计算构件的应力集中程度。基于等效结构应力的疲劳评估方法不仅具有良好的网格不敏感性，且其主应力幅-疲劳寿命（S-N）曲线为综合考虑大量焊接接头类型后提出，故该法具有较高的准确性。

本文针对各类荷载作用下含焊缝错边的构件，利用等效结构应力法对构件在不同母材板厚、错边距离和处理工艺下的疲劳性能进行研究，为带焊缝错边焊接件的疲劳性能评估提供参考。

1 错边处理方法

结合工程实际情况，对不同的错边情形和错边处理方式进行分析。对接焊缝模型（图2）基本尺寸为：母材厚度T为18，24 mm；纵向长度L11、L12均为200 mm；横向长度L2为80 mm。焊缝分析参数和错边处理参数设置分别见图3和表1。其中，e为错边量；h"为焊缝余高；l为堆焊斜边长；a为堆焊水平长度；i为堆焊坡度，i=e∕a；r为焊趾半径。参考相关规范［8-9］对于容许错边量和焊缝余高的规定，定义错厚比ε（ε=e∕T）、高宽比η（η=h"∕l，该值为负时表示焊缝下凹），并引入i、a和r作为参数。

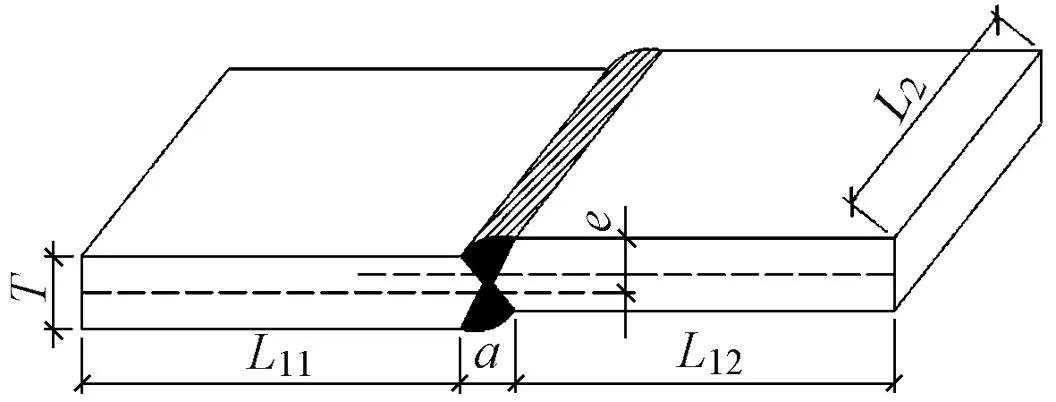
图2 对接焊缝模型

图3 焊缝分析参数

本文着重研究上述错边相关参数对结构疲劳性能的影响。为简便计算，忽略焊接变形的影响，假定焊接完成并通过矫形后两板件夹角为零。

表1 错边处理参数设置

2 基于等效结构应力的有限元模型

2.1 等效结构应力法

为了解决传统焊接接头评估方法对网格的依赖性，以及更好地表征焊缝接头影响疲劳的应力状态，根据结构力学理论，以静力平衡条件计算危险截面上的薄膜应力σm和弯曲应力σb，将二者之和定义为结构应力σs［10-12］。该方法为等效结构应力法，具有良好的网格不敏感性，计算公式如下

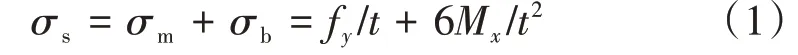
式中：fy和Mx分别为指定焊线上单位长度上的力和力矩，即线力和线矩；t为焊趾截面厚度。

基于断裂力学推导得到等效结构应力变化幅值ΔSs为

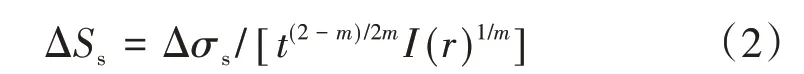
式中：Δσs为结构应力变化范围；I(r)为膜应力与弯曲应力状态；m为与材料有关的参数。

S-N曲线焊缝疲劳寿命公式为

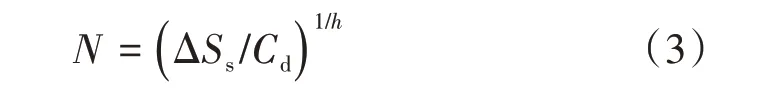
式中：Cd和h均为试验常数。

2.2 有限元模型

在有限元软件ABAQUS中采用实体单元（C3D8R）进行建模。母材、焊缝和熔合区的弹性模量均取E=206 GPa，泊松比υ均设为0.3。当受拉伸荷载作用时［图4（a）］，作用面积为1 440 mm2（模型厚度为18 mm时的横截面积），水平交变荷载最大值为100 MPa，最小值为10 MPa，即应力比为0.1；当受弯曲荷载作用时［图4（b）］，作用面积均为800 mm2（沿模型长度方向10 mm时的全宽面积），竖向交变荷载最大值为10.22 MPa，最小值为1.02 MPa，此时跨中附近截面最大名义应力为100 MPa，最小名义应力为10 MPa，即应力比为0.1；当受拉-弯组合荷载作用时［图4（c）］，将上述2种加载模式进行叠加，应力比仍为0.1。随后对模型进行网格划分，网格种子间距为3 mm。

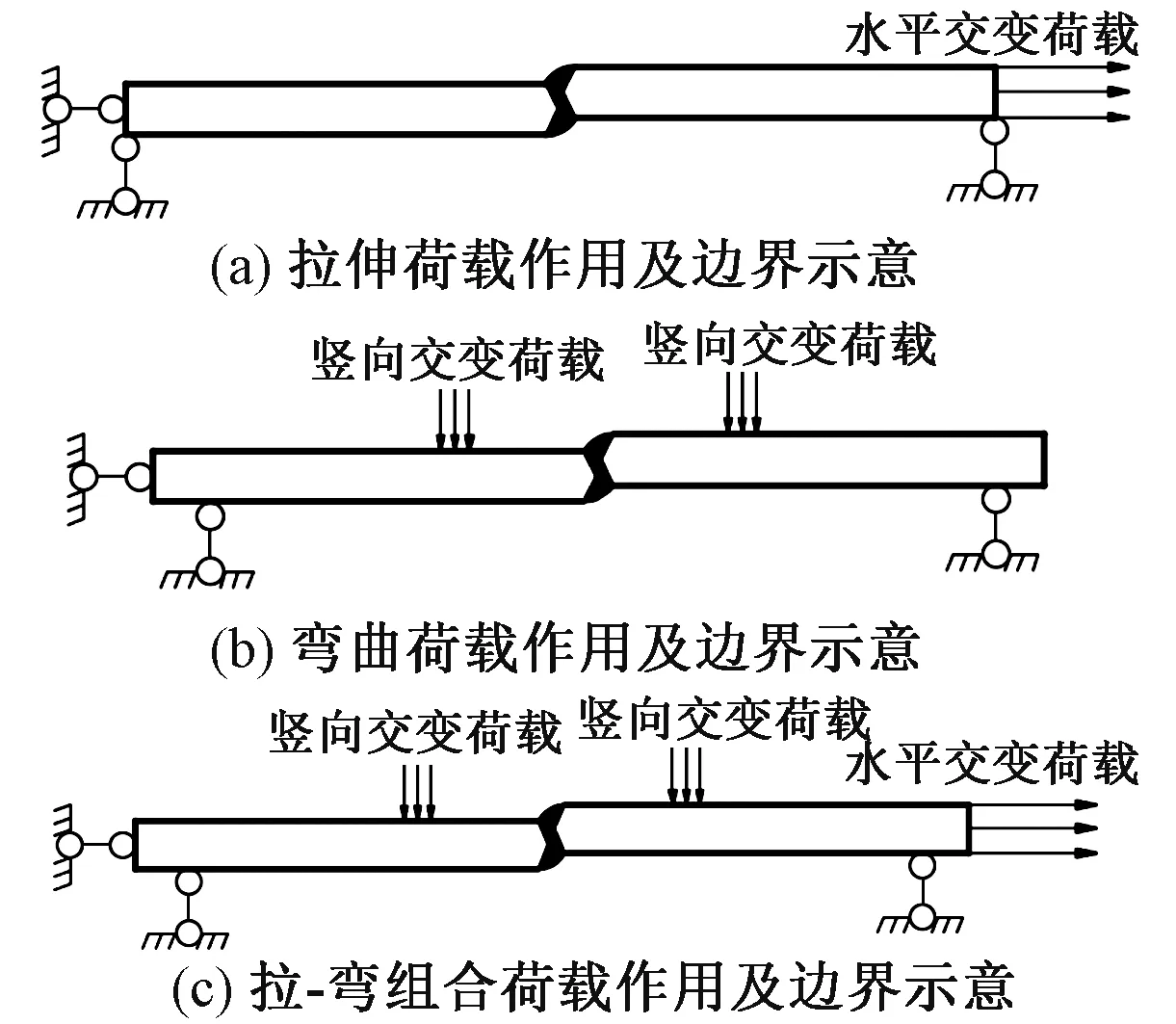
图4 错边有限元模型和模型加载

3 基于应力集中系数的焊缝错边分析

3.1 拉伸荷载作用

拉伸荷载作用下模型Mises应力分布见图5。采用式（1）通过提取线力和线矩计算关键部位结构应力后，再根据下式计算焊趾应力集中系数。

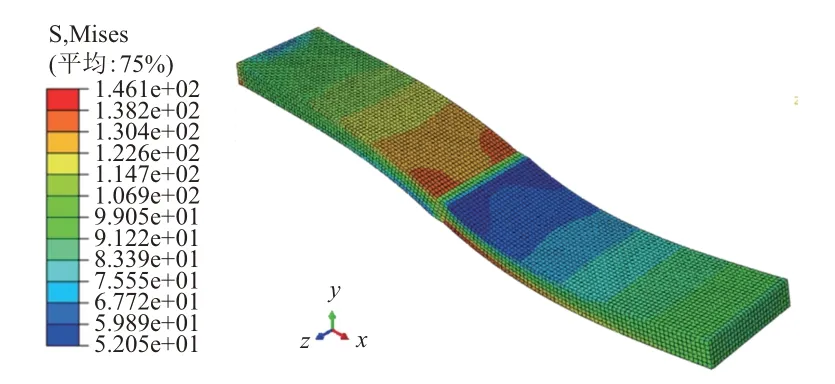
图5 拉伸荷载作用下模型Mises应力分布（单位：MPa）

式中：Ks为应力集中系数；σn为名义应力。

1）堆焊坡度。将堆焊坡度作为自变量，计算各错厚比模型对应的应力集中系数（图6），将高宽比和焊趾半径设为0，即焊缝无余高且不设置焊趾半径。由于堆焊坡度受错边程度即错厚比的限制，故各错厚比模型的应力集中系数变化曲线在各自对应的堆焊坡度范围内。

图6 不同堆焊坡度下各错厚比模型应力集中系数

由图6可知：①应力集中系数随错厚比的增加而增大，随堆焊坡度的降低而减小，错厚比越大该下降趋势越明显。以18 mm母材厚度模型为例，当错厚比为1∕2即错边量为9 mm时，堆焊坡度由初始坡度9∕10降至1∕8，应力集中系数总降幅可达20.3%。②在相同错厚比和堆焊坡度下，不同母材厚度的应力集中系数仅相差0.1%~4.5%，变化趋势接近。这表明采用错厚比定义错边程度具有一定可靠性。

在图6中对规范中的1∕8和1∕4坡度数据点进行了虚线标注。以18 mm母材厚度模型为例，并与不设堆焊坡度的模型进行对比：①当采用1∕8堆焊坡度时，错厚比为1∕2、1∕3、1∕6的应力集中系数分别减小25.2%、13.8%、3.2%；②当采用1∕4堆焊坡度时，错厚比为1∕2、1∕3、1∕6的应力集中系数分别减小8.4%、9.4%、0.8%。这表明1∕8堆焊坡度的应力集中程度的改善明显大于1∕4堆焊坡度。

2）焊缝余高。堆焊坡度i取1∕8和1∕4，母材厚度为18 mm，焊趾半径设为0，将高宽比作为自变量。由于不同错厚比模型的堆焊坡度不同，故其堆焊斜边长度也不同。为使焊缝余高选取合理，尽量将焊缝余高控制在-2~7 mm这一合理范围附近。计算不同高宽比下各错厚比模型应力集中系数，见图7。

图7 不同高宽比下各错厚比模型应力集中系数

由图7可知：①高宽比对应力集中系数的影响远小于堆焊坡度对其的影响，应力集中系数随高宽比的增加呈略微上升趋势，焊缝下凹对应力集中程度的改变几乎没有影响。以1∕8堆焊坡度为例，随着焊缝余高从0增加到7 mm，错厚比为1∕2、1∕3、1∕6时的应力集中系数仅增加了1.4%、1.3%、0.7%。②在相同错厚比下，不同堆焊坡度模型的应力集中系数相差约0.6%，变化趋势接近。表明采用高宽比定义焊缝高度具有一定可靠性。

3）焊趾半径。根据表1选择各错厚比的初始坡度，母材厚度为18 mm，焊缝余高为7 mm，将焊趾半径作为自变量。计算不同焊趾半径下各错厚比模型应力集中系数，见图8。

图8 不同焊趾半径下各错厚比模型应力集中系数

由图8可知，焊趾半径对应力集中程度的影响较小，随着焊趾半径的增大，应力集中系数略微下降。焊趾半径从0增加到8 mm时，错厚比为1∕2、1∕3、1∕6时，应力集中系数分别减小1.8%、1.8%、1.0%。

综上所述，在拉伸荷载作用下，采用不同方法处理焊缝错边，各错厚比模型的应力集中系数变化规律差别明显。其中，设置堆焊坡度对降低焊趾应力集中程度效果最为显著；焊缝余高会略微提高应力集中程度；设置焊趾半径会略微降低应力集中程度。

3.2 弯曲荷载作用

弯曲荷载作用下模型Mises应力分布见图9，采用式（1）和式（4）分别计算不同堆焊坡度和高宽比时模型的应力集中系数，结果显示应力集中系数均约为1，且各错厚比模型的应力集中系数相近。这表明在弯曲荷载作用下，焊缝错边疲劳性能对堆焊坡度、焊缝余高和错厚比并不敏感。由于在当前各类参数尺寸下，焊缝错边疲劳性能处于较优状态，基于本文的研究目的和实际工程意义，本节不再计算分析焊趾半径。

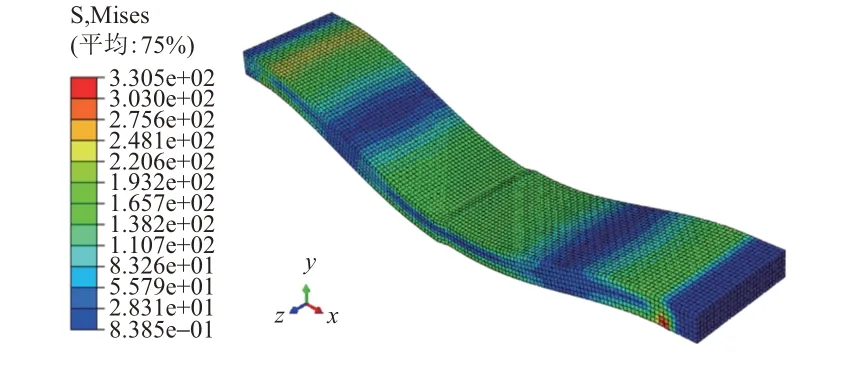
图9 弯曲荷载作用下模型Mises应力分布（单位：MPa）

3.3 拉-弯组合荷载作用

拉-弯组合荷载作用下的模型Mises应力分布见图10，此处组合荷载由2.2节中拉伸荷载与弯曲荷载直接叠加得到，即组合荷载名义应力为200 MPa，采用式（4）计算结构应力集中系数。

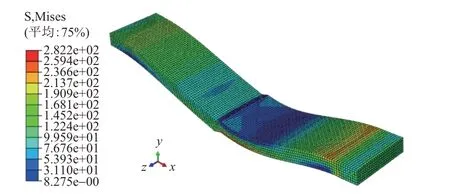
图10 拉-弯组合荷载作用下模型Mises应力分布（单位：MPa）

为与3.1节中的拉伸荷载模型相应计算值进行对比，以母材厚度18 mm模型为例，错厚比为1∕2和1∕3，将堆焊坡度作为自变量，计算不同堆焊坡度下模型应力集中系数，见图11。

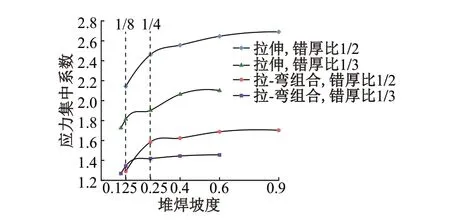
图11 不同堆焊坡度下模型应力集中系数

由图11可知，在拉-弯组合荷载作用下，焊缝应力集中系数变化趋势与拉伸荷载作用时一致。当错厚比为1∕2时，堆焊坡度由9∕10降至1∕8，应力集中系数降幅达24.2%。

当模型尺寸和错边程度均相同时，拉-弯组合荷载作用下的焊缝应力集中系数明显低于拉伸荷载作用时的对应值，如堆焊坡度为1∕8时，错厚比为1∕2、1∕3的焊缝应力集中系数分别减小约39.8%、25.8%。对比图5和图10可知，虽然在拉-弯组合荷载作用下模型的应力水平更大，但弯曲荷载的介入，焊缝处受力得到“缓冲”，使得模型应力分布更加均匀。结合3.2节分析结果可知，弯曲荷载基本不会加重焊缝应力集中程度。因此，与拉伸荷载作用相比，拉-弯组合荷载作用下焊缝应力集中程度更小。

为进一步揭示组合荷载中弯曲荷载与拉伸荷载各自占比对焊缝应力集中程度的影响规律，引入应力弯曲比，应力弯曲比=弯曲应力∕（薄膜应力+弯曲应力）。将薄膜应力与弯曲应力之和定为100 MPa，使得拉-弯组合荷载模型的应力与纯拉伸荷载时的应力一致。以母材厚度18 mm模型为例，堆焊坡度固定为1∕4，错厚比为1∕2和1∕3，计算不同应力弯曲比下各模型应力集中系数，见图12。

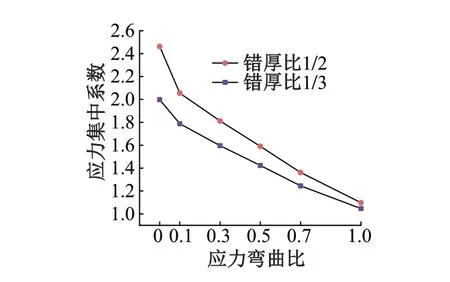
图12 不同应力弯曲比下各模型应力集中系数

由图12可知，随着弯曲荷载应力占比的增大，应力集中系数显著下降，且各错厚比模型的应力集中系数变化趋势一致。当应力弯曲比从0增加到1时，错厚比为1∕2、1∕3的应力集中系数分别下降约55.4%、47.6%。

4 基于疲劳寿命的焊缝错边分析

4.1 拉伸荷载作用

为进一步探究焊缝错边及处理方法对焊缝错边疲劳性能的具体影响，采用式（2）和式（3）计算模型受拉伸荷载时的疲劳寿命。参考文献［13-14］，选定m为3.6，Cd为23 885.8，h为0.319 50，I(r)为应力弯曲比的无量纲函数，I(r)=0.294r2+0.846r+24.815。拉伸荷载类型为疲劳交变荷载，最大应力为100 MPa，最小应力为10 MPa，即应力比为0.1，应力幅为45 MPa，计算得到此时无焊缝错边模型疲劳寿命为376.9万次。

本节在参数设置方面均与第3节应力集中系数对应部分保持一致，故直接给出计算结果。

1）堆焊坡度。不同堆焊坡度下各错厚比模型疲劳寿命见图13。可知：①焊缝疲劳寿命随错厚比的增加而减小，各错厚比模型的疲劳寿命均随堆焊坡度的减小而增加。②与无焊缝错边模型疲劳寿命相比，错厚比为1∕6、1∕3、1∕2时，疲劳寿命分别减小72.7%、88.9%、94.5%。③错厚比为1∕2时，堆焊坡度由9∕10降低至1∕8，总增幅可达93.4%。④堆焊坡度为1∕8时，错厚比为1∕2、1∕3、1∕6的疲劳寿命分别增加93.4%、36.7%、7.1%；⑤堆焊坡度为1∕4时，错厚比为1∕2、1∕3、1∕6的疲劳寿命分别增加29.5%、11.8%、1.0%。

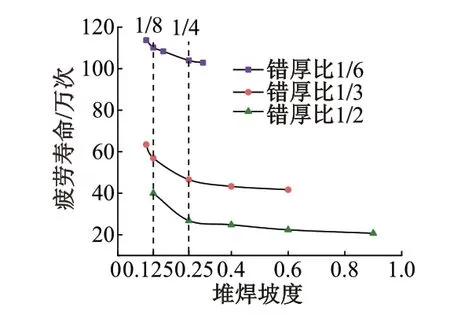
图13 不同堆焊坡度下各错厚比模型疲劳寿命

2）焊缝余高。不同高宽比下各错厚比模型疲劳寿命见图14。可知，高宽比对疲劳寿命的影响远小于堆焊坡度对其的影响，各错厚比模型的疲劳寿命均随高宽比的增加呈略微下降趋势。焊缝下凹对应力集中的改变几乎没有影响。焊缝余高从0增至7 mm，错厚比为1∕2、1∕3、1∕6时的应力集中系数分别增加3.7%、4.5%、2.0%。

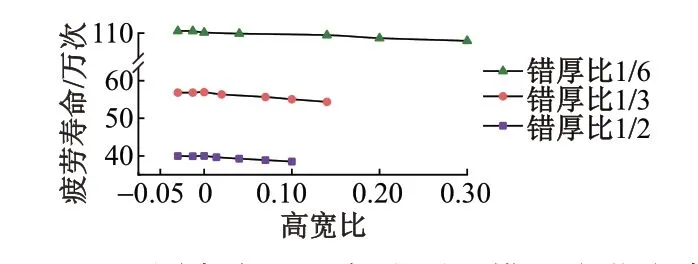
图14 不同高宽比下各错厚比模型疲劳寿命

3）焊趾半径。不同焊趾半径下各错厚比模型疲劳寿命见图15。可知，焊趾半径对疲劳寿命的影响较小，随着焊趾半径的增大，各错厚比曲线均呈略微上升趋势。焊趾半径从0增至8 mm，错厚比为1∕2、1∕3、1∕6时的焊缝疲劳寿命分别增加7.1%、4.7%、2.1%。

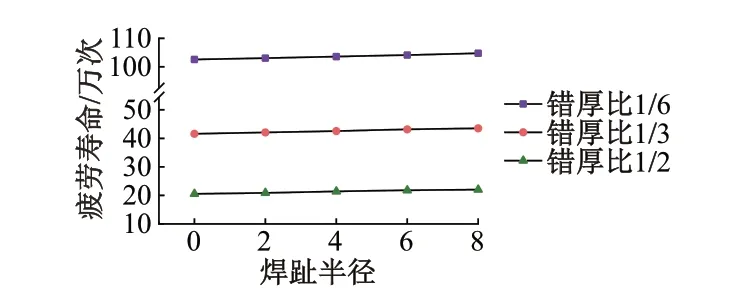
图15 不同焊趾半径下各错厚比模型疲劳寿命

综上所述，在拉伸荷载作用下，采用不同方法处理焊缝错边，各错厚比模型的疲劳寿命差别明显。其中，设置堆焊坡度对提高疲劳寿命效果最为显著；焊缝余高会略微减小疲劳寿命；设置焊趾半径会略微提高疲劳寿命。

4.2 拉-弯组合荷载作用

在弯曲荷载作用下，焊缝错边疲劳性能对错边量、堆焊坡度和焊缝余高并不敏感。因此，不再以弯曲荷载作用下模型为研究对象，直接对拉-弯组合荷载作用下焊缝错边的疲劳性能进行研究。拉-弯组合荷载类型参考图4（c），最大应力为200 MPa，最小应力为20 MPa，即应力比为0.1，应力幅为90 MPa。根据式（2）和式（3）计算得到拉-弯组合荷载下无焊缝错边模型疲劳寿命为16.6万次。不同堆焊坡度下各模型疲劳寿命见图16。

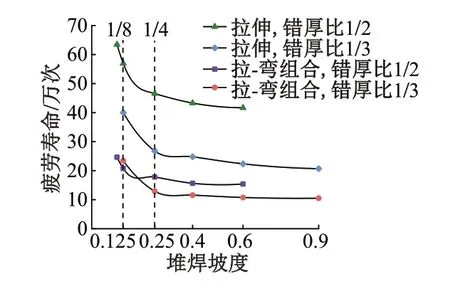
图16 不同堆焊坡度下各模型疲劳寿命

由图16可知：①在拉-弯组合荷载作用下，焊缝疲劳寿命随错厚比的增大而减小，且各错厚比模型的疲劳寿命均随堆焊坡度的降低而增大，该变化趋势与拉伸荷载作用时一致。②与无焊缝错边模型疲劳寿命相比，当错厚比为1∕3，1∕2时，疲劳寿命分别减小68.4%、78.5%。当错厚比为1∕2，堆焊坡度由9∕10降至1∕8时，疲劳寿命总增幅可达123.0%。③对比图13可知，虽然拉-弯组合荷载作用下应力集中系数更小，但产生的应力幅更大，故疲劳寿命反而更小。

为进一步揭示组合荷载中弯曲荷载与拉伸荷载各自占比对焊缝疲劳寿命的影响规律，引入应力弯曲比。将总应力设为100 MPa，使得受拉-弯组合荷载下模型的应力与受纯拉伸荷载时的值一致。以母材厚度18 mm模型为例，堆焊坡度为1∕4，错厚比为1∕2和1∕3，以应力弯曲比为自变量，计算各模型的疲劳寿命，计算结果见图17。

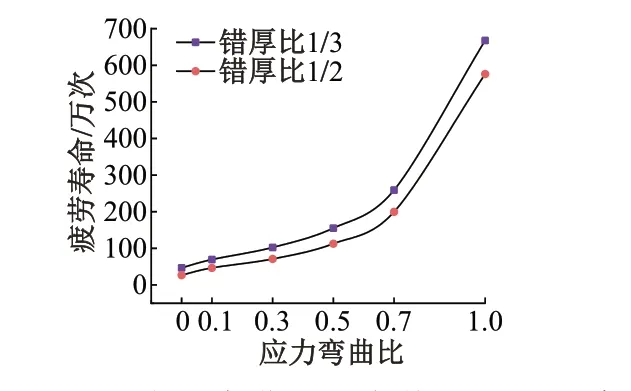
图17 不同应力弯曲比下各模型疲劳寿命

由图17可知，随着弯曲荷载应力占比的增大，疲劳寿命明显增加，且各错厚比模型疲劳寿命变化趋势一致。当弯曲应力比从0增加到1，错厚比为1∕2、1∕3时疲劳寿命分别增加2 051.6%、1 334.1%。表明在总应力水平不变的情形下，使错边结构分担更多的弯曲荷载，并降低所受拉伸荷载，会显著改善应力集中程度，增加疲劳寿命，提高疲劳性能。