2020年高考北京卷第20题的拓展探究
2021-06-07福建省莆田第十中学351146林清霞
中学数学研究(江西) 2021年6期
福建省莆田第十中学 (351146) 林清霞
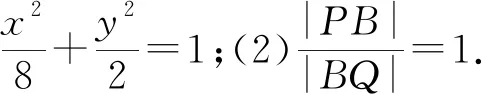
1.提出问题
2.特殊探路

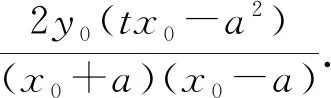
3.猜测论证

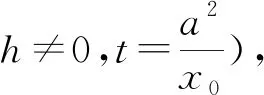

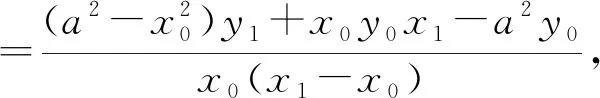



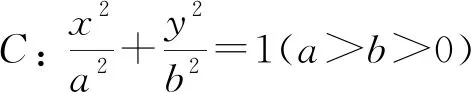
对于双曲线、抛物线,有类似的结论.


下面只给出结论3.1的证明.


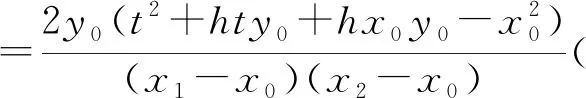

4.逆向拓展
结论1.1的逆命题成立吗?经过探究可得:
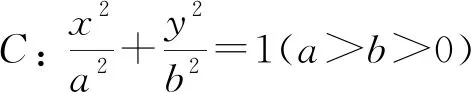

类似地,可得结论2.1、3.1的逆命题:

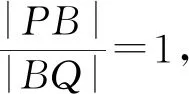
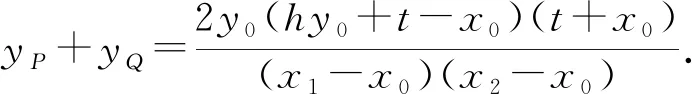
以上通过对一道高考试题的拓展探究,得到了椭圆、双曲线和抛物线的一类性质,揭示了问题的本质和规律,使学生经历了在教师指导下的“提出问题—特殊引路—猜测论证—逆向拓展”的探究过程,这无疑有助于学生对圆锥曲线问题的深度学习,有助于培养和提升学生的探究能力和数学学科核心素养.这正如《普通高中数学课程标准》(2017)所指出:“围绕某个具体的数学问题,发现和提出有意义的数学问题,猜测合理的数学结论,提出解决问题的思路和方案,通过自主探索、合作研究论证数学结论”,“在问题解决的过程中,理解数学内容的本质,促进学生数学学科核心素养的形成和发展”.
