基于立地因子的杉木人工林断面积生长混合效应模型研究
2021-06-07吴旭平张雄清朱光玉
吴旭平,吕 勇,张雄清,易 烜,朱光玉
(1.中南林业科技大学,长沙 410004;2.中国林业科学研究院林业研究所,北京 100091;3.青羊湖国有林场,长沙 410600)
0 引言
林分断面积是指林分中所有林木胸高断面积之和,作为常用的林分密度指标之一,具有较高的稳定性和预估性[1];因而,研究林分断面积生长对森林的收获预估具有重要意义[2]。
为了构建断面积生长模型,过去诸多学者对此进行了大量的研究,基础模型常常选用Richards和Schumacher方程,模型自变量主要包括年龄、密度、立地指数等因子[3]。其中李永慈等[4]研究得到:林分断面积生长模型是全林生长模型的核心,其精度直接影响到系统整体的预测精度。符利勇等[5]通过构建混合效应模型,有效解决了传统的建模方法无法反映不同立地水平及林分水平对蒙古栎(QuercusmongolicaFisch.ex Ledeb)生长的随机影响,从而导致精度低的问题。但目前将该方法应用于建立基于立地类型的杉木人工林林分断面积生长模型的研究较少。
湖南杉木(Cunninghamialanceolata)人工林面积和蓄积分别占湖南全省人工林面积和蓄积总量的33%和41%[6]。湖南是杉木人工林主要分布的区域之一,以该区域杉木人工林为研究对象,参考前人的研究,利用方差分析、回归分析法(最小二乘法)、非线性混合效应模型、K-means聚类等方法构建了基于立地效应的林分断面积生长模型,客观解释了立地因子对杉木人工林断面积生长的影响规律,提高了林分断面积生长模型的模拟精度,为湖南杉木人工林的科学经营管理提供了理论支撑。
1 研究区概况
湖南省位于我国中南部,地理坐标24°38′~30°08′N,108°47′~114°15′E。土地总面积21.18万km2,林地面积约1 300万hm2,活立木蓄积5.05亿m3,森林覆盖率59.57%[7]。海拔为24~2 122m,大部分地区海拔高度100~800m;年日照时数 1 300~1 800h;年平均降水量1 200~1 700mm,雨量充沛,水热充足。土壤类型以红壤和黄壤为主。研究区主要的乔木树种为杉木、马尾松(PinusmassonianaLamb)、湿地松(Pinuselliottii)、柏木(Cupressusfunebris)、樟树(Cinnamomumbodinieri)、木荷(Schimasuperba)、榉树(Zelkovaserrata)等。
2 材料与方法
2.1 数据来源
以湖南省150块杉木人工林样地为研究对象,在湖南省各市县设置杉木林样地进行调查。调查因子主要包括地理坐标、海拔、坡度、坡向、坡位、土壤类型、胸径、树高、林分年龄等。各因子统计如表1所示。

表1 杉木林分调查因子统计Tab.1 Statistics of stand factors for Cunninghamia lanceolata
2.2 立地类型划分
1)立地因子等级划分。
选用调查得到的海拔(HB)、坡向(PX)、坡位(PW)、坡度(PD)、土壤厚度(TH)、土壤类型(TL)等6个立地因子,并参照《测树学》[8]中的各类因子分级标准进行分级。其中,为了分析不同海拔对杉木生长的影响,将海拔按照100m进行分级[1]。具体划分标准如表2所示。

表2 立地因子等级划分Tab.2 Site factor classification
2)显著性分析及立地类型划分。
采用方差分析,以林分胸高断面积为因变量,以年龄和立地因子为自变量,进行显著性因子筛选[9];然后以显著性因子为对象,通过将分级之后的立地因子进行组合来划分立地类型(Site type),简称ST。
2.3 基础模型筛选
基础模型的选择影响林分断面积生长模型拟合的结果[10-11]。本文参考朱光玉等[12]构建林分断面积时所选用的基础模型,来作为本次湖南杉木人工林林分断面积生长预测的基础模型。候选基础模型如表3所示。

表3 候选基础模型Tab.3 Basic models candidates
2.4 非线性混合效应模型
非线性混合效应模型是回归函数依赖于固定效应参数和随机效应参数的非线性关系而建立的模型[13],其一般形式为:
Yi=f(β,μi,Xi)+εi
(1)
式中:Yi与Xi分别代表第i个样地的因变量向量和自变量向量;εi为误差变量;β和μi分别为固定效应参数向量和随机效应参数向量[14]。
2.5 模型精度评价
使用Forstat 2.2和R语言等软件进行数据统计,得到模型参数。用确定系数(R2)、平均绝对误差(MAE)、预估精度(P)、均方根误差(RMSE)、贝叶斯信息准则(BIC)及赤池信息准则(AIC)对模型的各个预测效果进行精度评价,其中MAE,RMSE,AIC,BIC值越小,且R2和P值越大,表明预测结果越好[15]。
确定系数:
(2)
平均绝对误差:
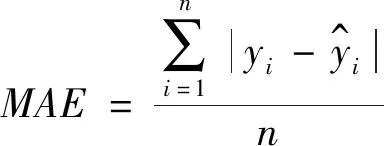
(3)
均方根误差:
(4)
预估精度:
(5)
赤池信息准则:
AIC=-2×lnl+2×p
(6)
贝叶斯信息准则:
BIC=-2×lnl+lnn×p
(7)

3 结果与分析
3.1 显著性分析及立地类型划分结果
采用方差分析,以林分胸高断面积为因变量,以立地因子和年龄为自变量,对立地因子进行显著性因子筛选[1]。当“Pr>F”的值大于0.05,即认为该因子对林分断面积影响不显著,否则影响显著,结果如表4所示。

表4 立地因子显著性检验Tab.4 Site factor significance test
由表4可得:HB,PD,PW,TH,TL对林分断面积的生长具有显著影响,其显著性顺序为TL>TH>PD>PW>HB。
以方差分析筛选所得到的HB,PD,PW,TH,TL为对象,通过对显著性因子的等级值进行组合划分,可将150个样地划分为107个初始立地类型(ST)。
3.2 基础模型模拟结果
1)林分密度指数计算。
林分密度指数为常用密度指标之一,常用于构建林分断面积[16],其表达式为:
SDI=N×(D1/D)β
(8)
式中:β为自然稀疏率,N为林分每公顷株数,D为林分平均胸径,D1为标准平均胸径(我国一般取D1=10cm),SDI为密度指数。
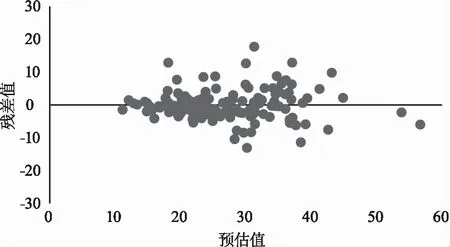
使用二次剔除不足立木度的样地方法来估算β。首先,建立回归方程lnN=a1-b1lnD,剔除lnN 具体公式为: lnN=α-βlnD (9) 在Forstat 2.2中对上述模型进行非线性拟合,最终得模型表达式如(10)式所示,其调整确定系数Ra2=0.71。 lnN=4.5273-0.96053lnD (10) 将所得自然稀疏率β=-0.96053结合相关变量代入SDI表达式即可计算各样地林分密度指数。 2)基础模型的拟合及最优模型确定。 以湖南省150块杉木人工林断面积-年龄数据为基础,利用Forstat 2.2对候选基础模型M1—M8进行参数拟合与筛选,得到不同基础模型参数估计值,拟合结果如表5所示。 由表5可知,模型M5:确定系数(R2=0.763 6)及P值(97%)最大,平均绝对误差(MAE=3.08)及均方根误差(RMSE=4.40)最小。可见,8个候选基础模型拟合结果中,模型M5拟合效果最好,因此,确定M5为最优断面积生长模型。公式为: 表5 候选基础模型拟合结果Tab.5 The fitting results of candidate basic models G=HT(a+b/T)×(SDI/1000)(c+d/T)×e(q+w/T) (11) 式中:G表示林分断面积;T表示林分年龄;SDI表示林分密度指数;HT表示林分优势高;a,b,c,d,q,w表示模型参数。 由于随机效应构造受随机因子个数及其水平数的影响,可以按任意方式相互组合衍生出多种类型的非线性混合效应模型。本文以主导因子划分的立地类型(ST)作为随机效应,构建非线性混合效应模型进行分析[18-19]。结合基础模型参数个数和立地类型,运用R语言的非线性混合效应模型板块,将立地类型分别加在各个参数上及同时加在多个参数上进行随机效应拟合,并利用评价指标AIC和BIC等确定最优模型结构,拟合结果如表6所示。 表6 基于立地类型的非线性混合效应模型拟合Tab.6 Nonlinear mixed-effect model fitting based on site type 由表6不同随机效应因子组合类型的拟合结果显示,构建单个参数及多个参数的混合效应模型的AIC,BIC相对基础模型M5有所降低,R2大幅提高。其中,立地类型(ST)作为随机效应加在参数c上面的混合效应模型R2(0.895 1)最高,AIC(872.41)、BIC(896.50)最低。因为基础模型是总体平均模型,而混合模型考虑了各种立地因子的影响。结果表明,基于立地类型的混合效应模型明显优于基础模型。 依据HB,PD,PW,TH,TL这5个主导因子,可将湖南杉木人工林划分为107个立地类型(ST),相应的混合模型随机效应参数有107个水平值。由于立地类型数过多,不利于混合模型的有效应用[1]。为了简化混合效应模型和进一步提高模型模拟精度,本文将初始立地类型(ST)应用到模型(11)式拟合的随机效应参数值进行K-means聚类得到立地类型组(Site Type Group),简称STG。进而构建基于立地类型组的非线性混合效应模型。 1)立地类型组的划分。 本文以聚类精度≥90%为标准,将107个立地类型的随机效应参数值进行聚类,随机效应参数值接近的立地类型合并成为立地类型组(STG),结果如表7所示。 表7 立地类型聚类结果Tab.7 Site type clustering results 由表7可得:聚类数为5的时候,聚类精度达到了91.0%,达到聚类精度要求。 2)基于立地类型组的非线性混合效应模型拟合结果。 运用R语言的非线性混合效应模型板块,将立地类型组分别加在各个参数上及同时加在多个参数上进行随机效应拟合,拟合结果如表8所示。 表8的拟合结果显示,基于立地类型组的非线性混合效应模型的AIC,BIC相对模型(11)式及基于立地类型的非线性混合效应模型均有所降低,而R2大幅提高。其中,立地类型组(STG)作为随机效应加在参数c上面的混合效应模型R2(0.920 2)最高,AIC(749.40)、BIC(770.48)最低。这说明,基于立地类型组的混合效应模型明显优于基础模型及基于立地类型的混合效应模型。最终模型为: 表8 基于立地类型组的非线性混合效应模型拟合Tab.8 Fitting of nonlinear mixed effects model based on site type group G=HT(a+b/T)×(SDI/1000)(c+ci+d/T)×e(q+w/T)+ε (12) 式中:G为林分断面积;HT为林分优势高;T为林分年龄;SDI为林分密度指数;ci为立地类型组的随机效应参数;ε为误差项。 将聚类后的立地类型组(STG)作为随机效应进行非线性混合效应模拟,利用MAE,RMSE,P,R2等4个评价指标进行模型评价,并与基础模型(None)、初始立地类型(ST)模拟结果进行对比分析,其结果如表9所示。 从表9中可以看出,在将聚类后的立地类型组作为随机效应加入模型后,林分断面积生长模型的R2值从0.763 7提高到0.920 2、提高了20.49%,MAE降低了17.21%,RMSE降低了14.77%。 表9 模型精度评价Tab.9 Model evaluation of three models 为了更加直观地对比基础模型与混合效应模型的模拟效果,分别建立最优基础模型(11)式和最优非线性混合效应模型(12)式的残差关系图,其结果如图1、图2所示。 图1 基础模型(11)式残差分布情况Fig.1 Residual distribution of the basic model(11) 图2 混合效应模型(12)式残差分布情况Fig.2 Residential distribution mixed effects model(12) type 从图1和图2可以明显看出:基础模型与混合效应模型的残差分布都较随机地分布于坐标轴两侧,无明显异方差现象;相比较基础模型(图1),混合效应模型的残差分布范围更小,且更加集中于坐标轴两侧。可见:基于立地随机效应的林分断面积模型可以极大提高模型精度,同时利用K-means聚类划分立地类型组的方法,可以进一步提高模型模拟精度且解决了复杂立地类型的模型使用问题。 采用方差分析、回归分析法(最小二乘法)、非线性混合效应模型、K-means聚类等方法构建含立地效应的湖南杉木人工林林分断面积生长模型,客观解释了立地因子对杉木人工林断面积生长的影响,提高了林分断面积生长模型的模拟精度。 1)采用方差分析,以林分胸高断面积为因变量,以立地因子和年龄为自变量,对立地因子进行显著性筛选,其结果表明HB,PD,PW,TH,TL对林分断面积的生长具有显著影响,其显著性顺序为TL>TH>PD>PW>HB。 2)通过使用回归分析法对8个候选基础模型进行模拟,其中Schumacher(M5)的确定系数最高(R2=0.763 6),因此,选择此方程作为林分断面积生长模拟的基础模型。 3)本文在确定基础模型之后,构建非线性混合效应模型,期望能得到湖南省杉木人工林林分断面积生长规律。结果表明,构建混合效应模型可以显著提高林分断面积建模精度,其确定系数(R2)从0.763 6提高0.895 1。胡松[1]用相同方法分析了不同林分类型与立地类型差异对栎类林分断面积生长的影响;李春明等[3]在对比传统的回归模型方法与混合模型方法构建落叶松云冷杉林分断面积模型之后,得到混合模型方法精度更高的结果。这充分说明运用混合模型方法构建林分断面积模型是合理且有效的。为方便建模,构建的断面积模型中仅考虑地形、地貌等立地因子的影响,未能考虑土壤、气候等因子的影响。在后续研究中,可考虑使用地形、地貌数据先构建杉木人工林立地指数模型求得各样地的地位指数,进而再考虑土壤因子构建断面积模型,或许模型精度会进一步提升。 4)通过K-means对立地类型进行聚类得到立地类型组,然后进行混合效应模拟。刘飞虎[20]采用此方法分析了不同林层对栎类次生林断面积生长的影响。由于聚类是指将不同的样本总体划分成不同的类型,及各类型的样本个体之间的差异尽可能小。所以本文构建的基于立地类型组的非线性混合效应模型可以进一步提高建模精度,其确定系数(R2)从0.895 1提高到0.920 2。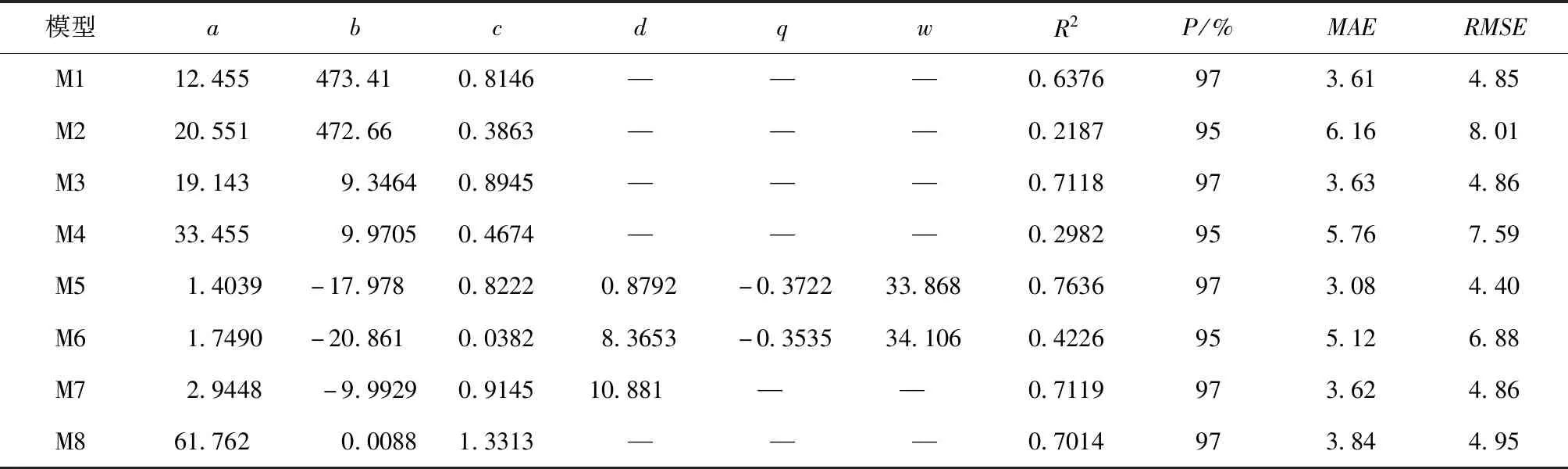
3.3 基于立地类型的非线性混合效应模型构建

3.4 基于立地类型组的非线性混合效应模型构建


3.5 模型精度评价


4 结论与讨论
