复合材料层合结构层向理论及应用进展*
2021-06-07沈海军
沈海军,李 伟,2
(1. 同济大学 航空航天与力学学院, 上海 200092; 2. 中国民航大学 航空工程学院, 天津 300300)
先进复合材料,相较于传统的金属材料,具有比强度高、比模量高、耐腐蚀、抗疲劳以及可设计性强等优点。在航空航天领域,飞机的主承力结构件已开始大量采用复合材料层合结构,其用量已成为衡量现代飞机先进性的重要指标之一。然而,一方面,由于飞机主承力构件中复合材料用量的增加,急需高精度的层间局部响应结果;另一方面,随着复合材料层合结构设计水平和整体成型工艺的不断提高,整体加筋复合材料层合结构、先进格栅增强层合结构及空间点阵复合材料层合结构的出现也对现有的复合材料层合板壳分析理论提出了严峻的挑战[1]。因此,复合材料层合板壳结构及其复杂整体成型结构的高精度板壳分析理论成为学者们研究的热点问题之一。
传统的板壳分析方法大多基于等效单层板(Equivalent Single Layer,ESL)理论。ESL理论通过对板壳结构沿厚度方向的变形特征进行适当的假设,将三维弹性理论转为二维问题进行分析处理。ESL理论主要有经典层合板理论(Classical Laminated Theory,CLT)、一阶剪切变形理论(First-order Shear Deformation Theories,FSDT)以及高阶剪切变形理论(Higher-order Shear Deformation Theories,HSDT)。ESL理论的位移场可统一简化表示[2]为:
(1)
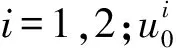
传统的等效单层板理论在薄板假设的基础上忽略了体积力的影响,是工程上一种应用广泛的层合板壳结构分析理论。其具有计算简便和未知量少等优点,对于薄板的力学问题往往能够较好地得到整体变形、临界屈曲载荷和固有振动频率等宏观响应结果。然而,随着对复合材料层合结构分析精度要求的日益提高,等效单层板理论已不能完全满足复合材料层合结构的工程需求,尤其是其在分析大厚度层合板及其局部的层间剪切效应时所带来的误差是不可接受的。例如,图1所示为复合材料层合结构相邻两层之间的层向横向应力示意图,根据力的平衡原理,层间横向应力分量在相邻的两层之间应满足连续性要求,即(σxz,σyz,σzz)k=(σxz,σyz,σzz)k+1。等效单层板理论中的位移假设模式是厚度坐标的连续函数,这使得其横向应变分量沿厚度坐标也是连续的,在相邻两层材料刚度不同的情况下,导致横向应力分量具有不连续性,即(σxz,σyz,σzz)k≠(σxz,σyz,σzz)k+1,与层间横向应力的连续性相矛盾。因此对于较厚的复合材料层合结构及其局部损伤问题,不但无法满足精度要求,甚至会导致错误结果。为此,Reddy将层合结构离散为若干个独立的数值层,并单独模拟每个数值层内的位移场,然后再利用层间的位移协调来建立整个层合结构的位移场假设模式,该建模思想即为层向理论(layerwise theories)。相较于等效单层板理论,层向理论的位移场沿层合结构的厚度方向呈C0连续性,即层向理论沿厚度方向仅位移是连续的,而应变(位移的一阶导数)在层间界面处是不连续的,从而保证了横向应力在层间界面处的连续性,而且层向理论的位移假设模式还能够准确反映截面的横向翘曲。

图1 层合板层间横向应力平衡[2]Fig.1 Equilibrium of interlaminar transverse stresses between laminates[2]
回溯层向理论的研究历史,Reddy等最早提出了一种针对厚板结构的基于位移的广义层合板理论(displacement-based laminated plate theory)[3-5]。近二十几年来,研究人员将Reddy的层向理论广泛应用于复合材料层合结构、压电复合材料层合结构以及功能梯度层合结构的静动力学分析中,并且不断地对层向理论进行改进和优化。目前,已有相关的书籍[2,6-9]系统地介绍了层向理论的基本原理及其数值分析方法,并且关于层合板壳理论的综述性文献[10-19]对层向理论也有所提及。然而文献调研发现,近年来还没有综述文献系统地介绍层向理论的最近发展及应用。为此,本文深入调查和研究了近年来层向理论的相关文献,系统性地介绍了层向理论的基本原理、发展情况、数值解法及应用现状,最后展望了层向理论的研究趋势和工程应用前景。
1 层向理论的基本原理及发展
迄今为止,许多学者们都基于层向理论的基本思想建立了相应的层向理论。例如:Carrera的统一理论(unified formulation)[20]、Ferreira的层向一阶剪切理论[21]以及Reddy的层向理论[22]。其中,最早提出的是Reddy的层向理论,其发展最为成熟,应用也最为广泛。因此,着重介绍Reddy的层向理论。通过将厚度方向上的插值节点分别布置于层合结构的层间界面以及上、下表面处,Reddy的层向理论的一般形式[2]为:
(2)
其中:(u,v,w)分别表示结构沿(x,y,z)方向的位移分量;(uk,vk,wk)为结构厚度方向上第k个插值节点处的位移分量;t为时间变量;N为层合结构中数值层的个数,因此厚度方向上含有N+1个插值节点,如图2所示;φk为厚度方向上的一维拉格朗日插值函数。
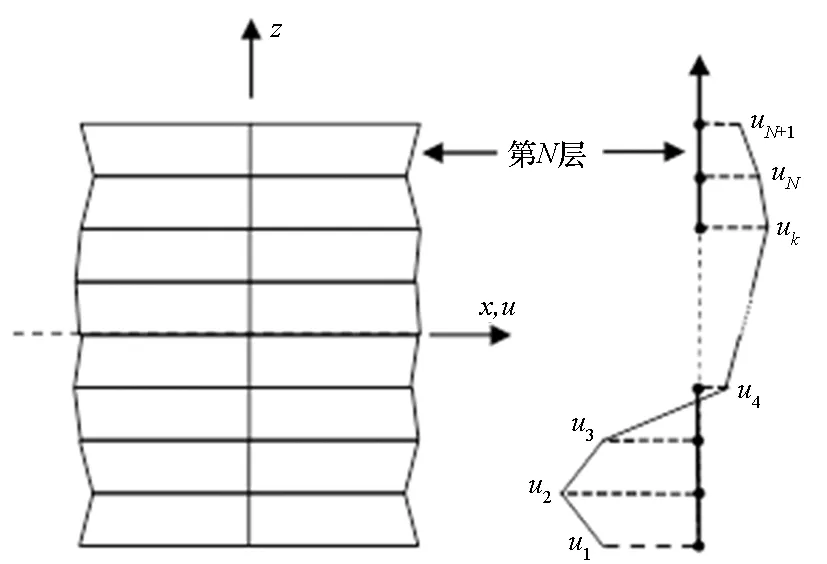
图2 层向理论位移假设模式Fig.2 Displacement approximation mode in layerwise theory
根据是否对横向位移进行层向离散,Reddy的层向理论可分为部分层向理论(partial layerwise theory)和全层向理论(full layerwise theory)两大类。部分层向理论,相较于等效单层理论,不但可以模拟面内位移沿厚度方向的Zig-Zag变化特性,还能够描述层间的横向剪切效应。而且与全层向理论相比,具有更好的计算效率。全层向理论在部分层向理论的基础上,还可以分析层合结构的层间正应力效应。
即便层向理论能够较为精确地描述中厚复合材料层合板壳结构的局部响应,但是由于需要在厚度方向布置足够多的插值节点才可以保证计算精度,因此,层向理论相较于等效单层板理论而言,计算工作量会大幅度增加。因此,近二十年来,研究人员不但从结构形式以及新材料的多场耦合等方面发展和丰富了层向理论,还提出了各种高阶非线性理论和混合方法,对层向理论进行了优化和改进。
1.1 结构形式
自从Reddy的层向理论被提出以来,学者们基于层向理论已经发展了各种结构形式的层向理论分析方法,主要包括复合材料层合梁、板、壳结构、加筋层合结构以及夹层结构等。
层向梁板壳理论是利用层向理论,结合不同结构形式的几何关系方程(应变-位移关系),发展得到的层向理论模型。针对复合材料层合梁及其压电智能结构,通过对面内位移进行简化处理,学者们采用层向理论相继建立和研究了层合梁、层合曲梁以及夹层梁结构。针对复合材料层合板壳结构,采用部分层向理论和全层向理论,研究人员相继提出和研究了复合材料层合板、夹层板、层合圆柱壳、层合双曲壳、层合环壳、层合球壳,层合扁壳、层合锥壳以及夹层壳等层合结构的层向分析方法。随着复合材料层合结构整体成型工艺的不断提升,层向理论也应用于大型复杂加筋复合材料层合板壳结构的精确分析模型中。例如,Li等[23]分别采用层向理论和有限元方法建立了复合材料层合圆柱壳结构的层向有限元模型和加强筋结构的三维实体有限元模型,进而通过圆柱壳和加筋结构连接节点处的位移协调和内力平衡关系耦合建立了整个加筋层合圆柱壳的层向有限元控制方程。采用上述建模思想,Li等[24]和Lu等[25]相继提出了复合材料夹层结构和加筋复合材料层合板的层向离散耦合分析方法。以上文献的研究结果均表明:基于层向理论的离散耦合分析方法在研究复杂复合材料层合结构问题时,能够得到更为准确的静动力响应结果,尤其在描述加强筋结构以及芯子的局部响应特性时,更具优势。
1.2 非线性
首先,早期大多数研究工作采用的是线性层向理论,计算效率不够高。另外,早期研究大多考虑线性几何关系,所建立的层向理论无法分析结构的大变形问题。为此,学者们相继从几何非线性以及高阶非线性两方面对层向理论提出改进。
采用几何非线性理论可以提高层向理论在分析复合材料层合结构大变形问题时的精确度。研究人员利用Von-Karman非线性应变-位移关系,分别提出了复合材料层合梁[26-28]、板[29-32]、圆柱壳[33-35]、圆锥壳[36]以及夹层梁板壳结构[37-40]的几何非线性层向理论。由于新材料在智能板壳层合结构领域得到应用,学者们相继研究了压电复合材料层合结构[41-42]、功能梯度材料层合结构[43-45]、形状记忆合金复合材料层合结构[46]以及多铁性复合材料层合结构[47]的几何非线性层向理论。以上文献研究结果表明:基于层向理论的几何非线性理论在分析复合材料及其智能层合结构的大变形和低速冲击问题时,不但能够获得精确的整体静动力响应结果,而且计算得到的层间局部响应量可更好地应用于模拟层间分层裂纹扩展特性研究。
在高阶非线性方面,Reddy等[48]最早将厚度坐标的二次拉格朗日插值函数引入层向理论的位移假设模式中,对线性层向理论进行了优化。Plagianakos和Saravanos分别将二次和三次插值函数引入复合材料夹层厚板结构的层向线性位移场的假设模式中,相继研究了其静态响应[49]和低速度冲击响应[50]特性;采用相同的建模方法,作者将其高阶层向理论应用于压电复合材料层合结构的机电耦合分析理论中[51-52]。Sun等[53]利用其高阶层向理论模型,研究了多层旋转叶片结构的动态响应特性。近年来,Rekatsinas等[54-57]采用三阶Hermite多项式样条函数来描述位移场分量沿厚度方向的分布,建立了含压电传感/作动器的复合材料层合板壳结构的层向机电耦合方程。Batra等基于三阶层向理论和几何非线性理论,分别提出了复合材料层合直梁[58]和曲梁[59]结构的高阶层向理论;研究结果表明:在不借助任何应力修正方法的基础上,其得到的横向应力结果与解析结果和三维弹性实体有限元结果吻合较好。
由于复合材料夹层结构的芯体厚度较大,因此较多采用高阶位移理论对芯体结构的位移场进行模拟假设。Loja等[60]基于不同的高阶层向剪切变形理论,分别模拟了面板结构和芯体结构的位移场,通过引入Kriging面内插值函数,建立了含黏弹性软质芯体复合材料夹层结构的层向/Kriging有限元控制方程。基于Loja的层向/Kriging有限元理论,学者们随后研究了复合材料夹层柱[61]、梁[62-64]以及板壳[64-65]结构的稳定性问题。
近年来,研究人员受到有限元理论的等参单元思想启发,将计算机辅助几何设计(Computer-Aided Geometric Design, CAGD)中用于表达几何模型的高阶B样条基函数作为形函数,并与层向理论相结合,形成了层向等几何高阶有限元方法[45,66-69]。
1.3 多场耦合
研究人员最早将温度场的假设模式作为独立变量引入层向理论中,通过材料的力-热本构关系方程来建立传统复合材料层合结构在热环境下的力-热层向耦合分析理论[32,36,70-75]。文献[44,76-79]基于层向理论分析了功能梯度材料板壳结构的静动力响应特性。另外,学者们[46,80-82]还采用层向理论研究了形状记忆合金复合材料层合结构的热屈曲特性。
Robbins等[83]最早采用层向理论建立了压电层合梁的机电耦合有限元模型,并且与基于等效单层板理论的有限元模型进行了静力学和模态响应结果的对比。其研究结果表明:相较于等效单层板理论的有限元模型,层向机电耦合有限元模型计算得到的静力学响应横向应力满足层间连续性要求;而且,在模态分析方面,层向机电耦合有限元模型对于高阶模态以及大厚度结构的分析结果更精确。Reddy等又相继建立了压电复合材料层合板的几何非线性层向机电耦合理论[84]和层向机电耦合混合板理论[85]。Heyliger等和Han等基于Reddy的部分层向理论,分别建立了压电复合材料层合圆柱壳[86]和平板[87]的层向机电耦合有限元模型。Li等在其基础上,采用全层向理论对位移场和电势场独立地进行模拟假设,分别提出了压电复合材料层合圆柱壳的全层向机电耦合有限元模型[88]和含分层损伤压电复合材料层合板的细化全层向机电耦合有限元模型[89]。
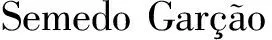
除了力热耦合和力电耦合的两场耦合以外,层向理论还被广泛地应用于三场及以上的耦合分析建模。文献[101-104]采用层向理论提出了压电复合材料层合梁、板、壳结构的力热电多场耦合层向理论。文献[105-108]则提出了智能复合材料层合梁和板结构的力电磁耦合层向分析模型。文献[109-110]还基于层向理论研究了智能复合材料的力-热-电-磁四场耦合效应。
2 层向理论的有限元解法
层向理论被提出以来,研究人员主要通过解析法、半解析法及有限元法等理论来求解和建立相应的层向分析理论。解析方法虽能够获得较为满意的结果,但较大程度受结构和加载形式以及约束条件等方面的制约。因此建立各种层向有限元分析方法成为该领域最主要、也是最具活力的研究方向之一。研究结果表明[2,10],层向有限元理论不但在分析精度方面与三维弹性有限元模型相同;而且相较于三维弹性有限元理论,还具有以下优点:①减少了系统的自由度;②由于层向有限元理论的面内离散和横向离散是独立进行的,因此可以根据计算精度需要进行选择性的优化,无须重新构建三维有限元模型。
研究人员从缩减系统总自由度和提高计算效率角度出发,对层向有限元提出了各种优化方法。学者们最早采用一种“整体-局部方法”的可变动力学单元模型。Robbins和Reddy[10,111]最早将层向理论和等效单层板理论结合,在局部(分层、边缘等)通过高精度的层向有限元模拟位移场,其余部分采用高效率的等效单层板模拟位移,建立了层合板壳的“整体-局部方法”的可变动力学有限元模型,其模型中的有限元网格划分模型如图3所示。模型中,内部整体区域采用FSDT单元建模,自由边区域的有限元模型采用层向理论,并且通过变形协调关系来保证局部与整体单元节点的连续性。基于相同的“整体-局部”建模思想,Botshekanan Dehkordi等[112-113]采用Reissner的混合变分定理,提出了夹层板结构的层向/等效单层板混合板理论。其他涉及“整体-局部方法”的层向有限元研究成果,可参考文献[67,114-119]。

图3 基于“整体-局部分析方法”的可变动力学有限元模型[10]Fig.3 Variable kinematic finite element model based on “global-local analysis”[10]
层向理论的另外一个优点是,如式(2)所示,每一个位移分量都可以独立地进行假设模拟,因此可以根据需要,对位移分量分别采用等效单层板理论、Zig-Zag理论或层向理论进行假设模拟,或者对位移分量采用不同阶数的级数展开式进行描述。例如,在文献[10]中,Reddy在保持面内离散单元不变的情况下,仅通过对横向插值函数进行细化,大大提高了复合材料层合板横向剪切应力的预测精度。文献[22,120-121]都基于该思想对层向有限元方法进行深入的研究。
此外,近年来采用不同的单元类型对层向有限元理论进行改进和优化也成为该领域的研究热点之一。Phung-Van等[122-123]提出了三节点三角形单元层向有限元理论,并用于分析复合材料层合板及夹层板结构的静动力学响应分析。Belarbi等[124]基于层向理论,建立了复合材料夹层板结构的四节点四边形等参元模型;其中,面板结构采用2自由度的节点,而芯体部分采用了9自由度的节点。相似地,文献通过各种单元优化方法,相继提出了复合材料夹层壳[125]、夹层玻璃光伏组件[126-127]以及含分层损伤的复合材料层合壳结构的层向有限元分析方法。
3 层向理论的应用
3.1 静力学分析
静力学分析是工程结构设计和应用的基础,其核心任务是精确预测结构在静态载荷作用下的响应量,如位移、应力和应变以及压电智能结构的电势分布等。相较于传统的等效单层板理论,层向理论能够更为精确地描述复合材料层合板壳结构,尤其是大厚度层合结构的静态响应特性。
Robbins和Reddy作为层向理论的奠基人,在文献[22]中详细地讨论了层向理论在分析复合材料层合结构静力响应方面的优势。针对大厚度复合材料层合板结构,采用层向理论深入研究了其局部响应特性。其中,以铺层顺序为[0°/90°/0°]的四边简支正方形层合板(长/厚=4)为研究对象,采用层向理论计算了在四边简支的边界约束条件下横向剪切应力分量σxz沿层合板厚度方向的分布,并与采用等效层合板理论(CLT和FSDT)和三维精确解的预测结果相比较,如图4所示。从图4中可以看出,基于等效单层板理论的模型在分析厚板结构的横向切剪应力时,与三维精确解相差较大,而层向理论与三维精确解几乎完全吻合;另外,从图4还可以看出,层向理论计算得到的层向剪切应力完全满足沿层间的连续性要求,而等效层合板理论给出的计算结果则不满足连续性要求。此外,文献[22]中还以铺层顺序为[45°/-45°/-45°/45°]的长条形层合板(长/宽=10,宽/厚=4)为研究对象,采用层向理论进一步研究了自由边效应。图5给出了在结构自由边附近的三个不同位置处,层向理论预测得到的横向剪切应力沿厚度方向的分布情况,可以看出横向应力完全满足在自由边处为零的条件。后来,学者们还相继分析了大厚度复合材料层合板[128]、圆拱[129]、双曲壳结构[130]以及复合材料夹层结构[37,49,131-133]的静力学特性;基于层向理论在分析自由边效应问题的优异性,学者们分别研究了反对称角铺设层合板[134]、非正交铺设复合材料层合板[135]、一般铺层形式复合材料层合板[136]以及复合材料胶接铺层结构[137]的自由边效应。
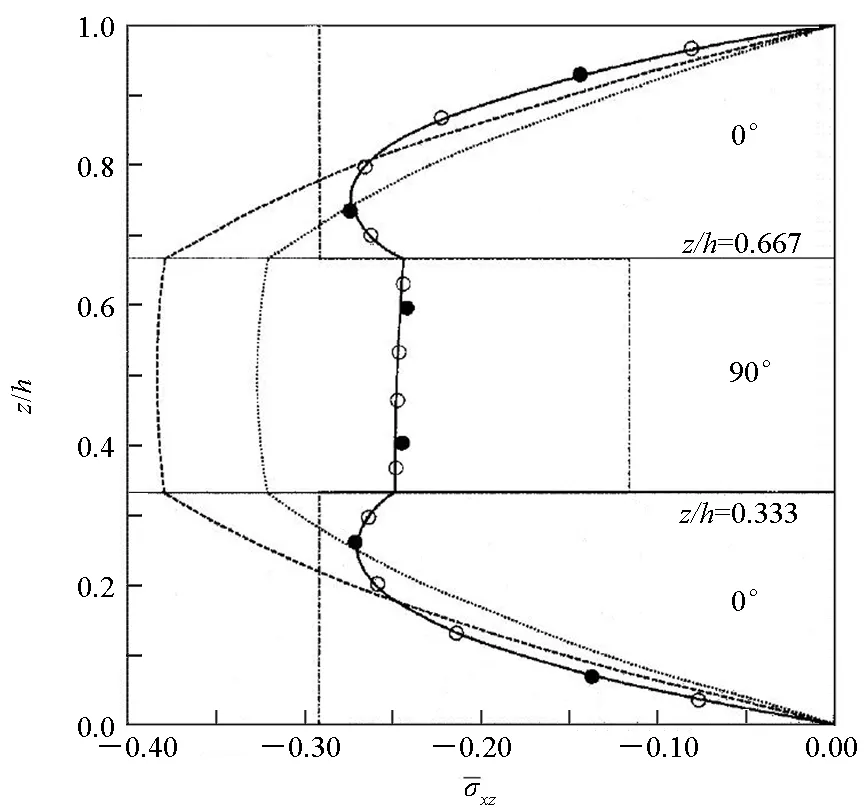
-- 三维精确解 ○ 层向理论(mesh 1)● 层向理论(mesh 2) CLT … FSDT图4 横向剪切应力沿层合板厚度方向的分布[22]Fig.4 Distributions of transverse shear stresses through the thickness of laminates[22]
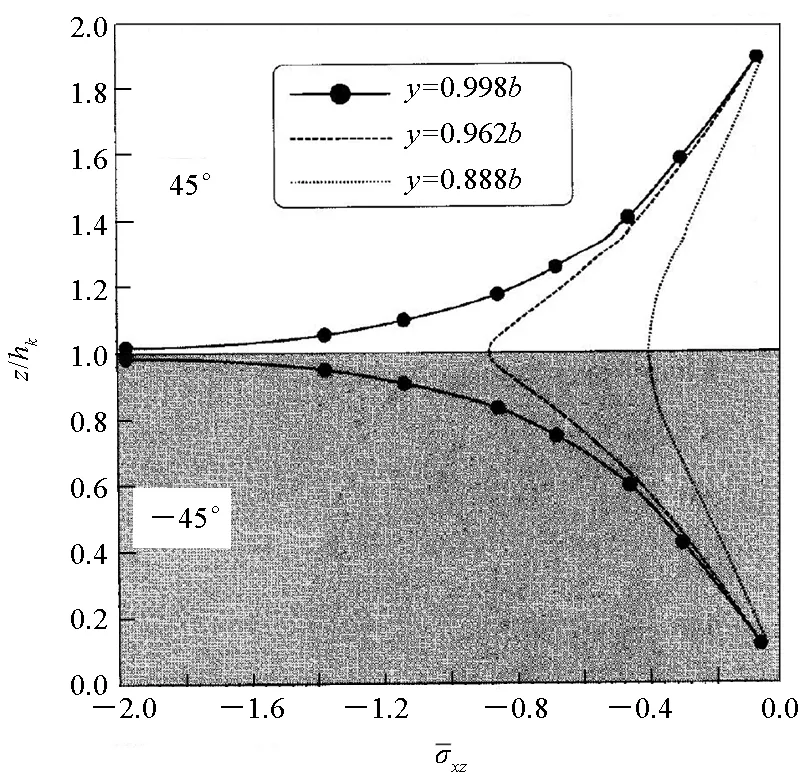
图5 横向剪切应力在自由边处沿层合板厚度方向的分布[22]Fig.5 Distributions of transverse shear stresses through the thickness of laminates near the free edge[22]
Heyliger等[86,138]最早将部分层向理论引入电势场的假设模式中,提出了含压电铺层复合材料层合圆柱壳和层合梁的层向静力学有限元模型,并分析了压电传感器对智能层合壳结构主动静力学响应特性的影响。Han等[87]同样采用部分层向理论,分析了压电作动器对智能复合材料层合板静态特性的影响。近年,Li等[88]采用了精度更高的全层向理论建立了压电复合材料层合圆柱壳结构的层向有限元模型,并深入研究了径厚比对智能结构的机械场和电场静态响应结果的影响。文献[51-52,91-92]均采用不同形式的层向理论深入分析了压电复合材料的静力学力电耦合特性。
3.2 振动分析
除了能够精确预测复合材料层合结构的局部静态响应以外,层向理论还被学者们广泛用来分析大厚度复合材料层合板壳结构的动态特性。Nosier等[139]最早将三维层向理论应用于各向同性单层板以及正交各向异性层合板的自由振动频率分析,并与等效单层板理论和解析方法的结果进行了深入的比较和分析。其研究结果表明:对于各向同性单层板,层向理论和等效层合板均能获得高精度的振动频率结果;然而随着正交各向异性复合材料层合板结构厚度的增加,等效单层板理论与精确解的误差逐渐增大,而层向理论依然能够保证精确的预测水平。后来,Zhang等基于层向B样条有限条法研究了复合材料层合板的自由振动特性,进一步验证了Nosier等[139]的研究结论。另外,文献也采用层向理论深入讨论了边厚比等参数对大厚度复合材料层合板[128,140-141]以及复合材料夹层板结构[142]自由振动频率的影响。
Shakeri等[143]较早地基于层向理论研究了大厚度压电功能梯度材料层合板的自由振动特性,作者重点讨论了跨厚比和组分体积比对压电智能结构固有频率及动态感应电势的影响。研究结果表明:基于层向理论的三维有限元分析方法能够精确预测大厚度压电功能梯度材料板的固有振动频率。基于Shakeri等[143]的研究,Pandey等[44]研究了热环境下功能梯度材料夹层板的自由振动特性,并分析了热载荷和几何尺寸等参数对结构固有频率的影响。学者们同样采用层向理论相继研究了含压电层大厚度复合材料层合梁[104]、板[100]以及夹层板结构[95]的动态特性。
近年来,考虑到层向理论建模能力强的特点,Li等[144-145]采用层向有限元和三维实体有限元分别建立复合材料层合面板和芯体结构的有限元振动方程,并利用面板和芯体结构之间的变形协调关系和内力平衡方程构建了整个夹层结构的层向/实体有限元振动控制方程,并通过与三维实体有限元方法进行比较,验证了该层向/实体有限元方法的正确性和优势性。Li等还将相同建模思想应用于加筋复合材料圆柱壳的自由振动特性分析[23]。
3.3 含损伤问题的分析
研究结果表明[146-147]:层间分层和基体裂纹已成为复合材料层合板壳结构最常见的两种损伤形式。由于层向理论能够更精确地描述复合材料板壳结构层间局部响应特性,因此结合层向理论建立复合材料层合结构的局部损伤模型以及分析其静动态响应特性成为层向理论非常重要的应用之一。
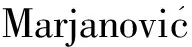
文献[152-154]研究了含分层损伤压电智能复合材料层合结构的静动态响应特性,尤其是分层损伤对感应电势分布的影响。近年,Li等[89]在Barbero等[148]层向分层损伤模型的基础上,考虑层间应变分量的不连续性,建立了含分层损伤压电复合材料层合板的层向细化有限元分析方法,分析了分层损伤尺寸和位置对于压电智能结构电势场的分布;而且如图6所示,获得了含分层损伤层合结构所特有的张开型模态,并进一步讨论模型在复合材料层合结构的损伤监测和定位方面的应用。

(a) 25%
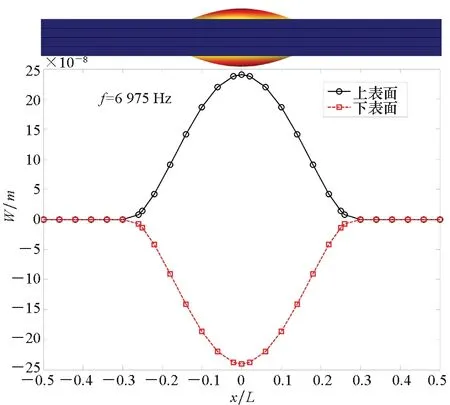
(b) 50%
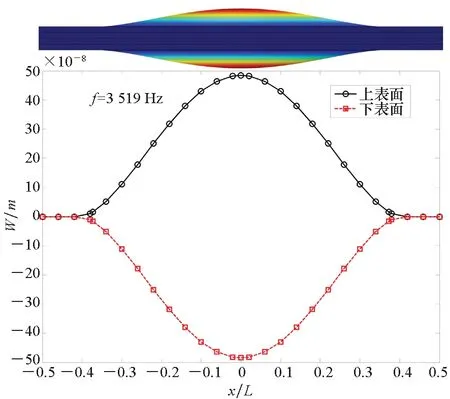
(c) 75%图6 不同分层损伤程度下压电复合材料层合板的张开型模态[89]Fig.6 Opening mode shapes of plates with various delamination sizes[89]
层向损伤扩展分析模型的研究目前主要集中于层间分层裂纹的扩展行为预测[155-157],而采用层向理论同时分析分层和基体裂纹扩展行为的较少。Li等在Barbero等[148]层向分层损伤模型的基础上,利用扩展有限元方法(eXtended Finite Element Method, XFEM)来描述基体裂纹,提出了一种扩展层向理论(eXtended LayerWise Theories, XLWT),对同时含有层间分层裂纹和基体裂纹的复合材料层合梁[158]、板壳[159-160]以及双曲壳[161]结构的静态断裂行为进行了深入的分析和讨论,其中,含分层复合材料层合壳基体裂纹任意扩展时的位移和应力云图如图7所示,图中位移和应力均为无量纲。近年,Li等进一步提出了力热耦合的XLWT[162],实现了热环境下分层和基体裂纹同时任意扩展的高精度预测。
另外,学者们[29,50,57,163-167]还将层向理论应用于复合材料层合结构在低速冲击载荷作用下的动力学响应和失效特性分析。

(a) u1 (b) u2 (c) u3
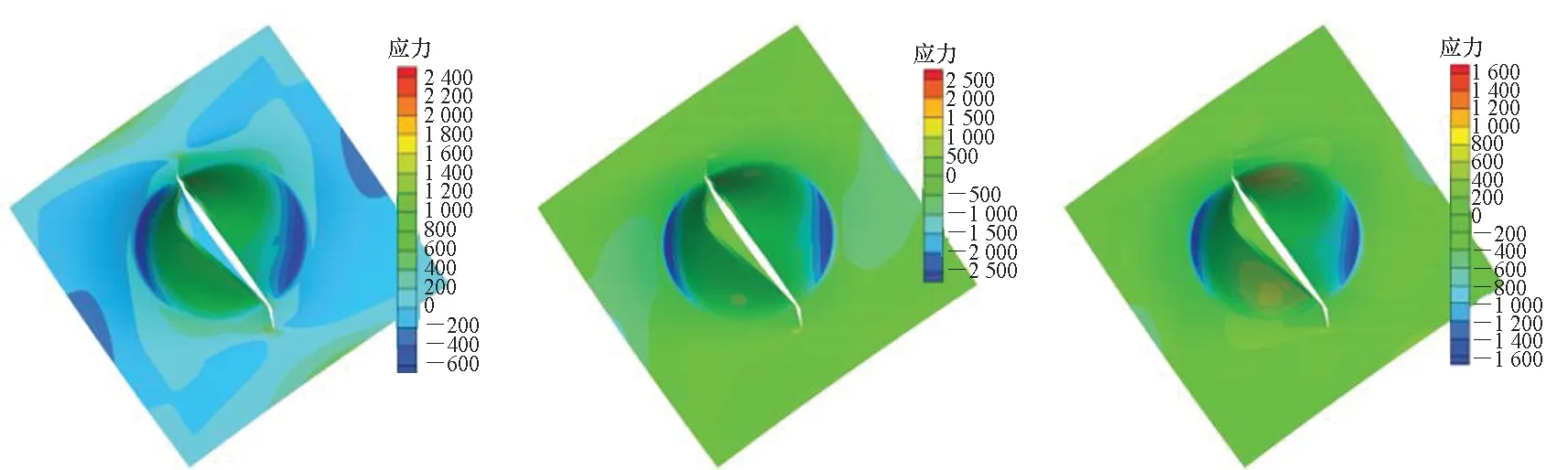
(d) σ11 (e) σ22 (f) σ12 图7 含分层复合材料层合壳基体裂纹任意扩展时的位移和应力云图[161]Fig.7 Cloud pictures of displacements and stresses for the laminated shell with crack and delamination[161]
4 层向理论研究方向展望
层向理论具有理论简单、易于编程实现等特点,并且还易于扩充至任意的多场耦合问题,再加之其便于与其他数值理论相结合,因此层向理论无论在理论发展还是在工程应用上都具有广阔的研究前景。
1) 将层向理论与XFEM结合,建立复合材料结构的多损伤分析模型。目前,只有很少的文献将层向理论与XFEM结合,用于分析复合材料层合板壳结构的分层和基体裂纹扩展问题。因此,有必要进一步考虑孔洞、夹杂等间断问题,提出含多种损伤形式的复合材料层合结构的层向扩展有限元分析方法。
2) 基于层向理论的无网格方法。由于层向有限元方法在处理几何不连续性等问题时的计算效率和精度不够理想,因此可以考虑结合无网格方法,提出一种层向无网格分析方法,用于高效模拟复合材料层合结构的大变形和几何不连续问题。
3) 层向理论在智能结构损伤监测和主动控制领域的应用。目前,很多学者已经采用层向理论构建了压电智能复合材料结构的力电耦合关系。因此,结合层向理论在局部的高精度电势预测水平,可一步扩展应用于含压电传感器智能层合结构的损伤监测研究;再结合适当的控制领域,可以建立含压电作动器的智能结构的层向主动控制模型,用于精确分析压电智能层合结构的变形和振动控制问题。同样的思想可用于构建含磁致伸缩材料或形状记忆合金材料等其他智能结构的主动控制模型。
4) 复杂复合材料层合结构的层向理论模型。目前,层向理论绝大多数应用于形式较为简单的层合板壳结构;虽然有部分学者通过有限元节点连接技术实现了加筋层合结构的建模,但是随着复合材料设计和制造水平的提高,可以通过结合适当的连接技术,如固连接触法和面面接触法等,实现层向理论在复杂复合材料层合结构(如空间点阵复合材料夹层结构和格栅型复合材料结构等)领域的应用。
