水下串联立管涡激振动特性分析
2021-06-07王杰文左继泽余雄飞
刘 野 王杰文 左继泽 李 鑫 余雄飞
(1.海洋石油工程股份有限公司,天津 300000;2.深圳海油工程水下技术有限公司,广东 深圳 518067)
0 引言
随着世界各国对海洋探索的不断深入,深水油气藏资源成为各国争夺资源的主战场。在水下油气的开采项目中,立管铺设是极为关键的一部分,它主要负责连接水上组块平台和水下井口,并完成采出液的运输工作[1]。由于立管在水下容易受到风速、浪高和流速的共同作用,因此它会发生振动,严重时会导致立管管体发生疲劳受损甚至破坏。当立管受到外界流体的冲击时,在管道流体内部会产生漩涡,当释放的漩涡对立管施加力的频率与立管的固有频率相接近时,管道会发生共振现象,从而导致结构振动响应增大。在建设水下油气田的工程中,多立管组合形式的立管群被广泛应用,串联、并联等多种组合形式的立管群大大减少了施工时间,更有利于后续的管理和维护。立管群中的立管尾流会产生相互作用,立管管壁会发生多变且随机的振动,这种现象会加速结构的机械损坏,严重缩短立管的使用寿命[2]。
该文将ANSYS作为模拟软件,针对串联立管的管道内涡激振动进行数值模拟,分析在不同顶部约束条件下,结构的振动响应和结构参数的变化。
1 数学模型
ANSYS进行流体流动模拟时遵循三大守恒定律,根据求解问题的不同,需要选择合适的组分守恒定律与湍流方程。因为进行双向流固耦合要对结构进行计算,所以模拟时还需要满足动力学基本控制方程。
1.1 控制方程
1.1.1 质量守恒方程
质量守恒方程的微分方程如公式(1)所示[3]。
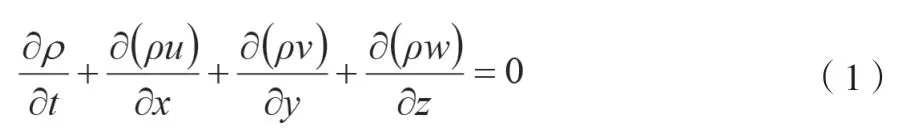
引入矢量符号
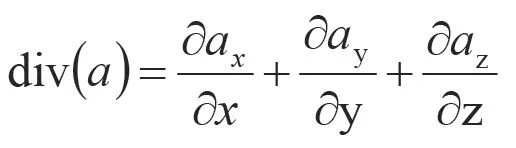
公式(1)可以写成如公式(2)所示。

式中:ρ为密度;t为时间;u、v和w为速度矢量u在x、y、z方向上的分量。
1.1.2 动量守恒方程
动量守恒方程如公式(3)~公式(5)所 示。
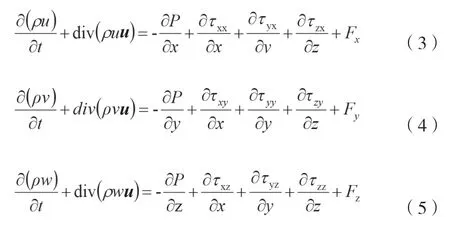
式中:P为流体微元体上的压力;τxx、τxy和τxz为因分子黏性作用而产生的作用在微元体表面上的黏性应力τ的分量;Fx、Fy和Fz为微元体上的体力,如果体力只有重力,且在z轴向上,那么就有Fx=0、Fy=0和F2=-ρg;g为重力。
1.1.3 结构动力学控制方程
采用有限元法解算结构运动方程对运动方程进行有限元离散,如公式(6)所示。

1.2 湍流方程
ANSYS为使用者提供了多种湍流方程,对于结构近壁处以及尾流的模拟大多采用SST k-ω。SST k-ω 模型与k-ε 模型相比,它更加接近实际工况,对管道内涡激振动的振幅、振频响应以及相关特性参数的模拟更准确,因此选用SST k-ω 的湍流模型。
SST k-ω 模型的计算公式如公式(7)所示。

式中:φ1为改进的内部边界层k-ω 模型;φ2为标准的k-ω模型;F1为混合函数。
1.3 几何模型及网格划分
立管的外部流域为1个六面体,流场长40D、宽20D,L/D=5。直径为18 mm、长 为3.6×103mm的细长圆柱,壁厚为2.5 mm,底端固定在流场底部,圆柱体顶面为自由端[4]。流场的入口流速为0.1 m/s,流体介质为水,密度为1 025 kg/m3,雷诺数为1 845。
采用ANSYS对几何模型进行双向流固耦合模拟,考虑到计算量、分析网格质量以及模拟形变区域,该文决定采用扩散光顺法的动网格技术。由于雷诺数较高且立管周围的流动情况比较复杂,因此需要对圆柱进行“O”型分块,对圆柱壁面网格进行加密,如图1所示。
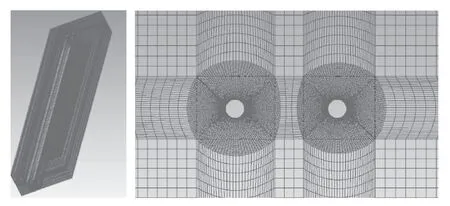
图1 串联立管外流场(左)及边界层网格(右)
2 模拟结果及讨论
2.1 流场数值模拟方法验证
在应用ANSYS进行流固耦合模拟之前,需要对无耦合情况进行数值模拟[5],并将模拟获得的立管横向位移时间历程和运动轨迹图与实验结果进行对比。通过分析对比结果可以确定所采用的网格划分方式、时间步长、湍流模型和数值模拟方法是能够准确对立管内涡激振动现象进行数值模拟的。立管自由端横向振幅如图2所示,可以看出实验结构的横向位移较大,约为±0.73D,数值模拟得出横向振幅约为±0.71D。数值模拟得出的斯特劳哈数约为0.191,与B.sannati实验结果吻合较好。
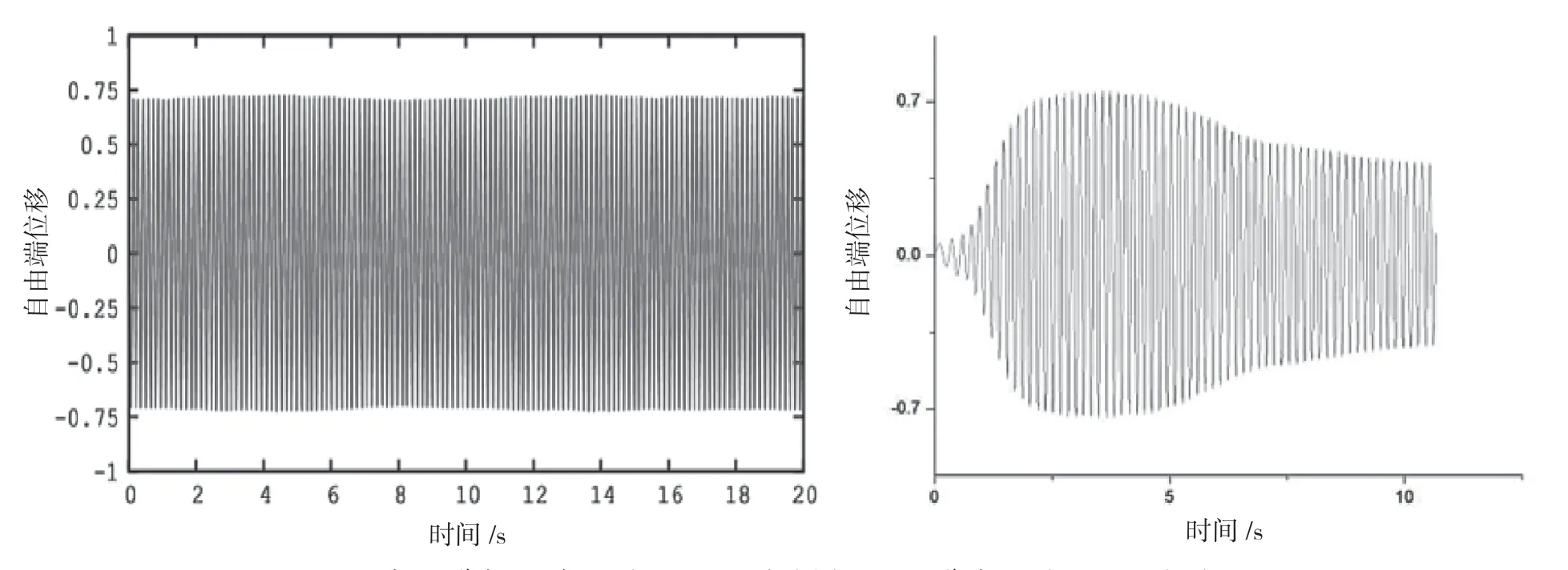
图2 实验立管自由端横向位移时间历程曲线(左)和FSI立管横向位移时间历程(右)
2.2 不同顶部约束条件下立管振动参数分析
图3和图4为不同顶部约束条件下立管升、阻力系数幅值的变化曲线。当对管道施加的顶部约束增加时,管道的上下游升力系数也明显增大,下游管道提升的幅度要更明显一些。主要是因为上游立管释放的涡流附着在下游立管上,下游管道受到上下游涡流的共同作用,会出现顶部张力增加、结构的固有频率增大、结构的响应幅度减小、能量耗散减少以及结构上下游压差增加的情况,从而导下游立管的升力系数的最大幅值约为上游立管的1.5倍。对于阻力系数,上游管道的尾流并没有增加管道内流体对结构的作用力,由于上游立管尾流的速度要小于正常流速,因此下游管道受到上游管道和自身脱落的旋涡的共同作用,会使下游立管顺流向的压力差不断地变化,从而导致下游立管的阻力系数小于上游阻力系数且幅值相差较大。
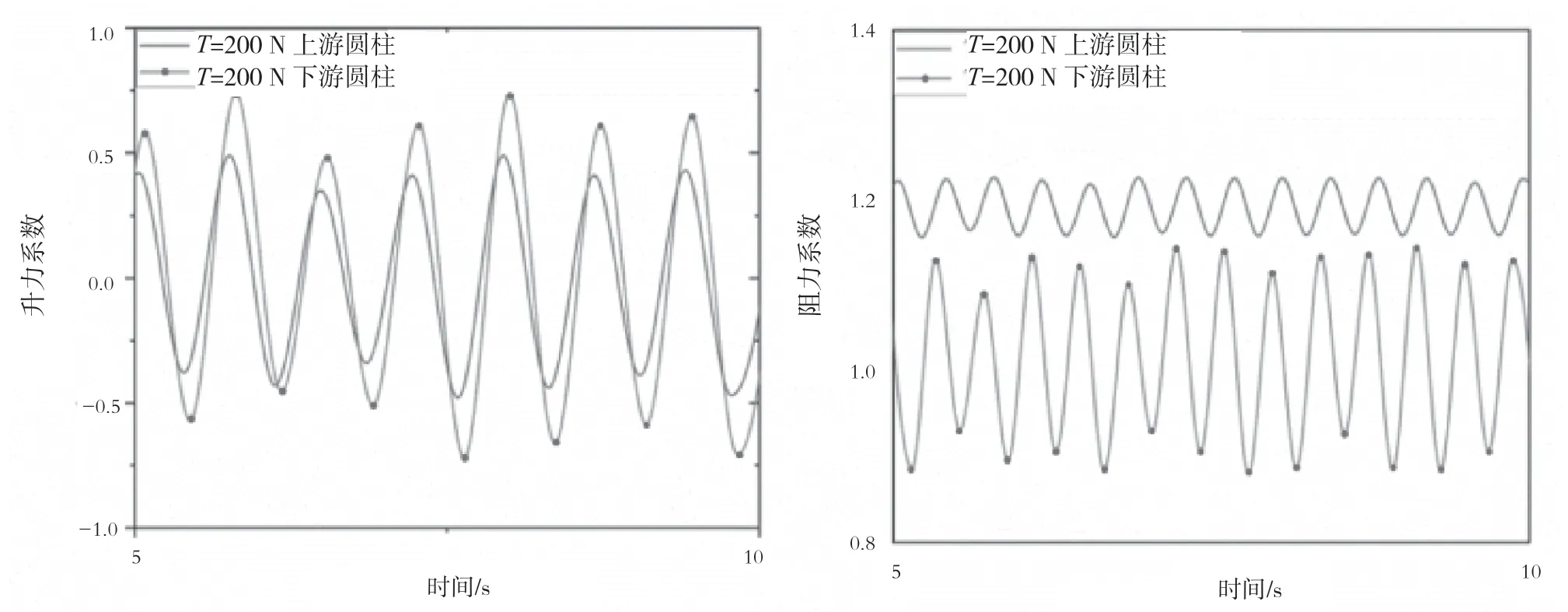
图3 T=200 N时串联立管升力系数(左)与阻力系数(右)
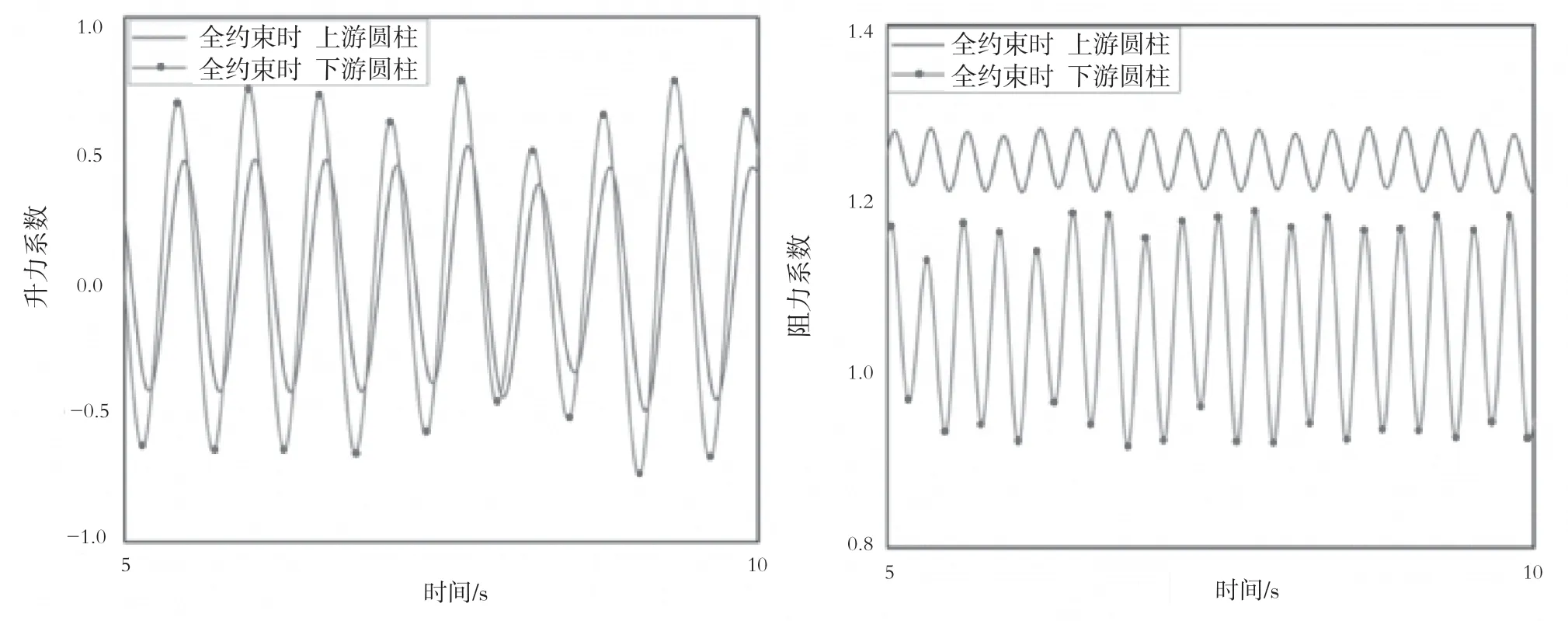
图4 顶部全约束时串联立管升力系数(左)与阻力系数(右)
通过模拟得到的升、阻力系数幅值随时间变化的曲线表现出周期性的特点,立管上下游的升、阻力系数的变化频率基本不随顶部约束的变化而变化,升力系数变化频率约为阻力系数变化频率的1/2,下游立管的频率幅值要远小于上游立管的频率幅值。
2.3 不同顶部约束条件下立管振幅与振频分析
在模拟的过程中,横坐标为沿着管道轴向提取的5个不同高度,关注点位置相对于管长比例分别为Z/L=0.1、Z/L=0.3、Z/L=0.5、Z/L=0.7以及Z/L=0.9,纵坐标为均方根与立管直径之比(Xrms/D、Yrms/D)。不同顶部约束条件下上下游立管的顺流向与横流向沿立管轴向高度的均方根振幅曲线如图5、图6所示。管道振动均方根振幅曲线呈对称的抛物线状,管道上下游都呈现出先增加后减小的趋势,在抛物线对称中心(Z/L=0.5)产生最大的均方根振幅,越靠近两端,振幅响应幅度越小。随着顶端载荷的不断增大,均方根振幅曲线逐渐趋近于直线,振动偏离初始位置且振幅程度减弱。在顺流向上,管道上游对下游产生“屏蔽”效应,下游立管的均方根幅值远小于上游立管;横流向下游立管受到上游立管和自身释放的涡流的共同作用,均方根振幅大于上游立管。
不同顶部约束条件下上下游立管的振动响应频率会改变管道的顶端约束,管道结构主要呈现出多频振动的现象,同流向上下游管不同位置的振频相同。随着立管顶端载荷的不断增加,顺向流立管的振动响应频率也不断增大,横向流立管的振动响应频率不变。因此,虽然增加顶端约束可以减小立管振动幅度,但是也会增大立管的响应频率,当响应频率接近于结构的固有频率时,结构发生共振的风险增高,这样会降低设备的使用寿命,严重的可能会造成管体损坏。
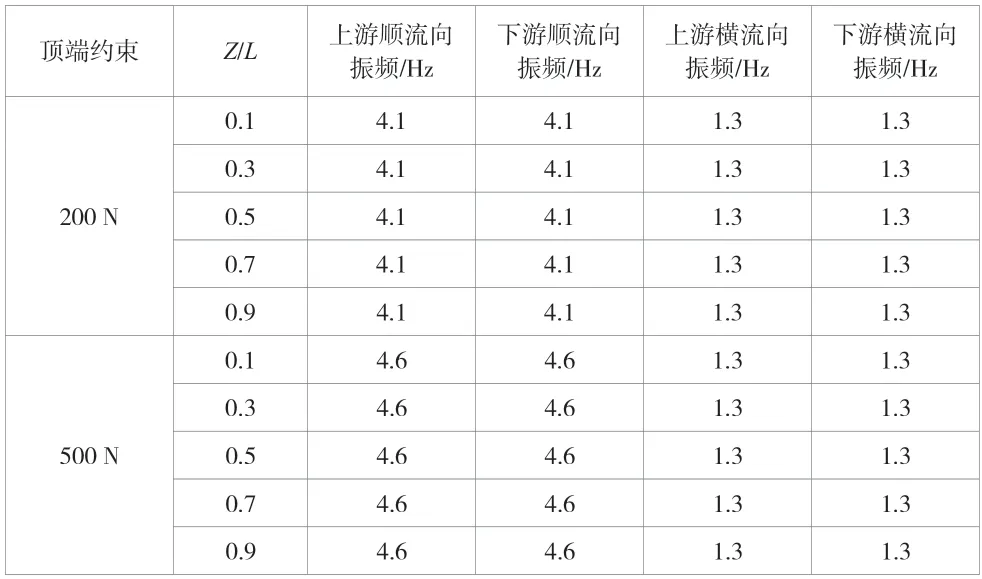
表1 不同顶端约束下串联立管振频
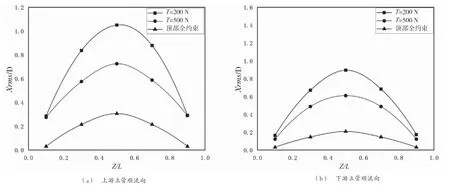
图5 不同顶部约束条件立管顺流向均方根振幅
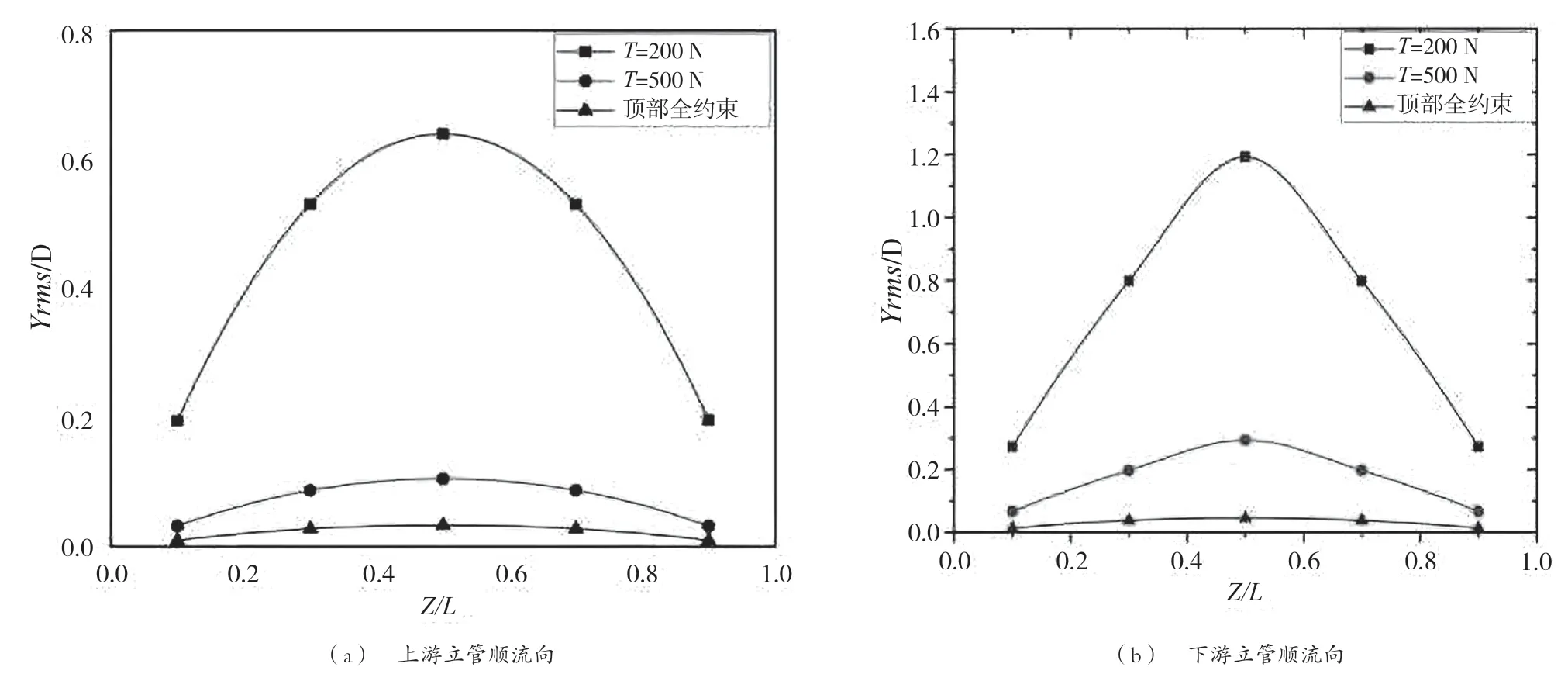
图6 不同顶部约束条件立管横流向均方根振幅
3 结论
该文对不同顶部张力的串联立管涡激振动时尾流的干涉效应进行模拟,得到的主要结论如下:1)应用ANSYS对无耦合情况下的圆柱扰流流场进行数值模拟,模拟获得的立管横向位移时间历程和运动轨迹图与B.sannati实验结果吻合较好,模拟得出的斯特劳哈数约为0.191,可以证明数值模拟结果的准确性。2)随着立管顶端约束的不断增大,立管上下游升、阻力系数呈现增加的趋势。下游管道受到来自上游管道和自身释放的涡流的共同作用,升力系数最大幅值远大于上游管道(约为上游管道的1.5倍);对于阻力系数来说,上游管道的尾流速度小于正常流速,并且受到上游立管与自身脱落的涡流的共同作用,下游立管阻力系数小于上游阻力系数,阻力系数变化频率大约是升力系数变化频率的2倍。3)随着顶端载荷的不断增大,均方根振幅曲线逐渐趋近于直线,振动偏离初始位置且振幅程度减弱。在顺流向(X方向),管道下游受到来自管道上游的“屏蔽”效应,下游立管的均方根幅值远小于上游立管;在横流向(Y方向),下游立管受到上游立管和自身释放的涡流的共同作用,导致下游立管的均方根振幅大于上游立管。4)对比不同约束条件下的振动频率图,立管结构主要呈现出多频振动的情况,不同位置的振动频率相同,顺流向的振动频率要大于横流向的振动频率。随着立管顶端载荷的不断增加,立管的振动响应频率也不断增大。因此,虽然增加顶端约束可以减小立管的振动幅度,但是也会增大立管的响应频率,当响应频率接近结构的固有频率时,结构发生共振的风险增高,这样会降低设备的使用寿命,严重的可能会造成管体损坏,因此选择合适的顶部张力也是值得研究的问题。
