智能计量设备通信模块可靠性评估方法研究

赵雪松 谢倩娴 尹仕红 侯 婧 张日取

（1.深圳供电局有限公司计量管理所，广东 深圳 430223；2.华立科技股份有限公司，浙江 杭州 310023）

0 引言

随着智能电网发展和智能计量设备的普及应用，智能计量设备运行可靠性的问题越来越多，对计量贸易结算造成了重大影响[1]。目前全国众多计量设备生产单位对智能计量设备的可靠性进行了研究，例如物料平台健全管控、自动化检测测试、间歇性故障研究、设计可靠性、零部件筛选以及生产工艺控制等，但这些研究以各企业自己的产品为研究对象，研究对象单一；同时，企业也不会公开发表相关的研究成果，因此不能推动整个计量设备行业的发展，进而严重影响了计量设备的健康发展[2-3]。随着智能计量设备可靠性的发展，目前对马尔可夫过程的研究也更加深入，马氏过程模型的研究受到了越来越多的重视。在现实世界中，有很多过程都是马尔可夫过程，从概率角度来看，对智能计量设备的可靠性水平进行评估和预测，可以保证通信模块有效、安全地运行[4]。该文从其最原始的数学定义出发，逐步讨论它的转移概率矩阵、初始概率分布以及在时刻m的概率分布，详尽阐述公式所表达的意义以及公式的应用方法。目前，马尔科夫过程的“无记忆性”（过去对于预测将来是无关的）已经广泛应用于对相关行业可靠性的评价和预测等领域。该文从计量设备的可靠性出发，基于计量设备通信模块（计量终端上行通信模块）的失效建立了失效数据分布数学模型，从而对失效进行评价。

1 马尔科夫链

1.1 马尔科夫链基本概念

如果离散空间K和离散时间的随机过程F（t）为K={k1，k2，…}，那么对于任意时刻有0 ≤t1＜t2＜…＜tn，在tn时概率可以由条件概率定义，如公式（1）所示。

1.2 状态转移概率矩阵

设某随机过程满足马尔科夫过程，即满足公式（3）的要求。

对于由n个状态组成的状态空间，它的转移概率可以表示为如式（4）所示的矩阵。

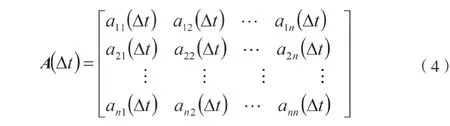
式中：A（Δt）为时间间隔Δt内状态空间转移函数；ann表示第n个状态空间想第n状态空间的转移概率。

公式（4）具有的性质如公式（5）所示。

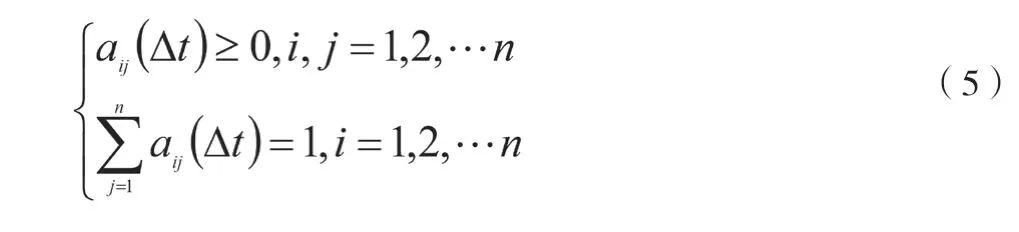
式中：aij（Δt）为时间间隔Δt内状态ai与aj间的转移概率函数。

如果t1，t2，t3…tn的时间间隔（Δt）相同，那么根据齐次性，概率矩阵A如公式（6）所示。

式中：aij为该状态的概率；A为该空间整体样本状态概率。当样本数量趋向于无穷大时，可根据ti及ti+1时刻状态的变化，获得满足误差要求的系统状态转移概率矩阵A。每增加1组样本，矩阵A内就可能会有一行值发生变化，行数对应ti时刻的系统状态，理论上，当样本数量足够大时，A的统计值就可以无限接近于真实值。

2 通信模块失效分类及状态

2.1 通信模块失效分类

在实际运行时，智能计量设备通信模块发生的某种故障可能是由1种或多种故障模式造成的，其故障机理过程是物理、化学、机械或生物等组合在一起的过程。通过故障机理分析，从根本上提高计量终端通信模块的可靠性[5]。智能计量设备的典型故障都是由软件、硬件引起的，下面以计量终端上行通信模块为例，通过失效机理分析，对通信模块进行分类，见表1。

表1 通信模块故障表

2.2 通信模块状态

将通信模块安装在运行现场后，当通信模块处于或趋近于不满足可靠性准则要求的运行状态时，运维人员将采取必要措施，确保智能计量设备的通信恢复到可以接受的水平。可以根据通信模块的生命周期，对其不同状态进行分类，根据通信的实际情况，可以将其运行状态分为正常状态、故障状态和风险状态。当出现正常状态和故障状态时，都需要采取必要的措施，但是目前无有效措施可以对风险状态进行管控[6]。状态1（运行状态）：在该状态下，通信模块无故障，通信正常。状态2（风险状态）：在该状态下，存在部分出现失效风险的模块，需要进行排除才能保证通信正常。状态3（故障状态）：在该状态下，通信模块出现失效，智能计量设备通信异常，需要维修或更换通信模块。

3 通信模块的马尔科夫链模型

3.1 通信模块的3运行状态模型

通信模块的3运行状态模型的状态空间为K={1，2，3}，其状态转移过程如图1所示，其转移矩阵如公式（7）所示。

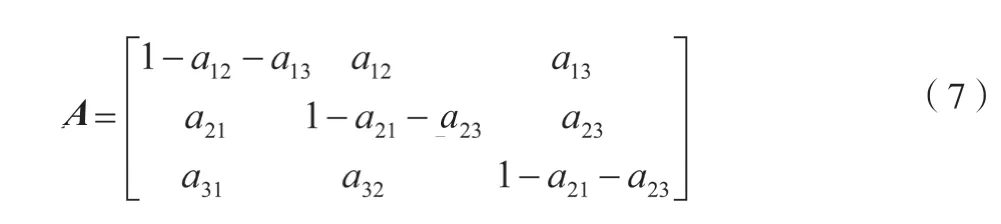
式中：aij为通信模块从i状态转移到j状态的概率。

3.2 通信模块m步状态转移

行向量Π（i）为ti时刻的通信模块通信状态分布，其定义如公式（8）所示。

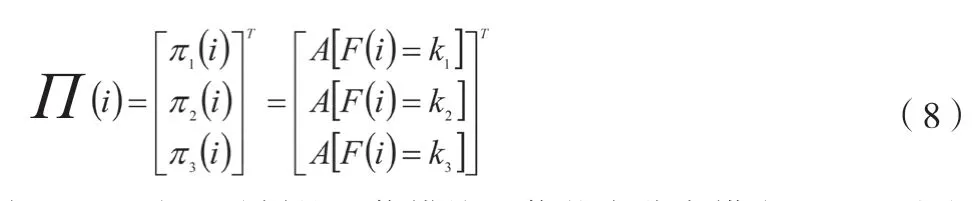
式中：Π(i)为ti时刻的通信模块通信状态分布横向量；πα（t）为ti时刻的通信模块α状态分布；T为终止时刻；T为终止时刻；[F（i）=k1]为i状态下的概率为ki。

假设通信模块的初始状态为Π（0），由状态转移概率矩阵A的定义，经过Δt后，下一个时刻的通信模块状态分布，如公式（9）所示。

显然，再经过Δt后通信模块状态转移，如公式（10）所示。

以此类推，经过m个Δt后的通信模块转态转移如公式（11）所示。

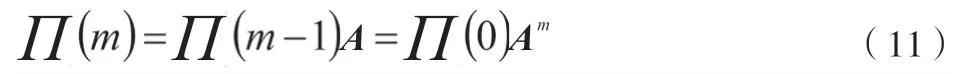
在已知Π（0）和A的前提下，可以通过快速解析来获得未来每隔Δt时间间隔后通信模块状态分布的失效率。

3.3 通信模块正常状态概率

当时间间隔的数量n→∞时（模块理论寿命），通信模块的可靠性趋近于某一稳定值，即通信模块的生命周期最终失效率如公式（12）所示。

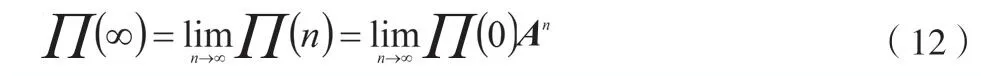
式中：An为n次迭代。

理论上，开始状态概率表示通信模块投入运行，此时失效率为0，但是存在部分风险状态的通信模块，此时的失效概率接近于πi（0），可以该根据电子产品的可靠性寿命串联模型对该数据进行预计（参考SN29500标准），如公式（13）所示。

式中：λ为产品失效率；λref为元器件基本失效率；πU为电压影响因子；πI为电流影响因子；πL为环境影响因子；πQ为元器件固有质量影响因子。

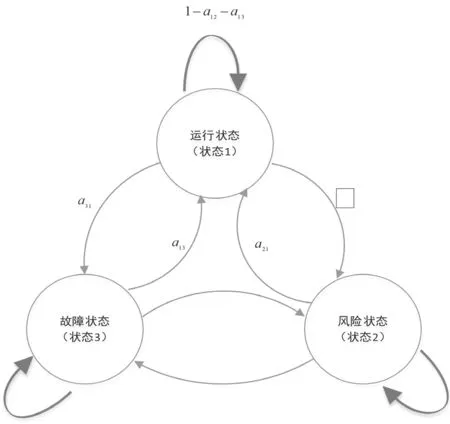
图1 通信模块状态转移过程图

当通信模块开始状态概率存在时（如公式（14）所示）。

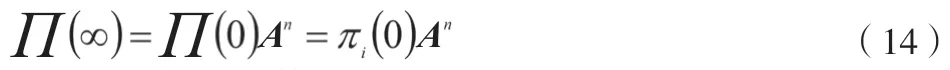
式（13）有如下等效变换，如公式（15）所示。

由于公式（14）的n个方程中只有n-1个独立，因此，需要与公式（15）联立求解，得到通信模块的正常状态概率，如公式（16）所示。

3.4 通信模块可用度

根据通信模块的运行情况，将其状态空间K分为通信状态W（工作状态）和故障状态U，记为W={e1.e2}，U={e3}。

通信模块可用度D（i）定义为ti时刻通信模块处于通信状态概率，如公式（17）所示。

因此，公式（7）可以表示为相应的矩阵形式，如公式（18）所示。

式中：B为通信模块在通信状态时失效概率的二阶方阵；C为通信模块从风险状态向故障状态转移的概率；D为通信模块失效概率向风险状态转移概率；E为通信模块故障状态向通信状态的转移概率，即修复概率。

3.5 通信模块首次失效前平均时间

将通信模块的故障状态置为静止状态，即令公式（19）中的D=0，就可以得到一个新的马尔科夫模型，那么通信模块首次失效前的平均时间如公式（19）所示。

4 算例分析

该算例只为验证智能计量设备通信模块运行的马尔科夫特性，根据标准要求，通信模块寿命为5 a，因此设Δt时间间隔内通信模块故障率为0.0002，修复概率为0.01，其他故障概率均为0。通过对某批次通信模块的状态及在Δt时间间隔内的分布和相邻时间间隔通信状态的变化进行了300次统计，结果见表2。

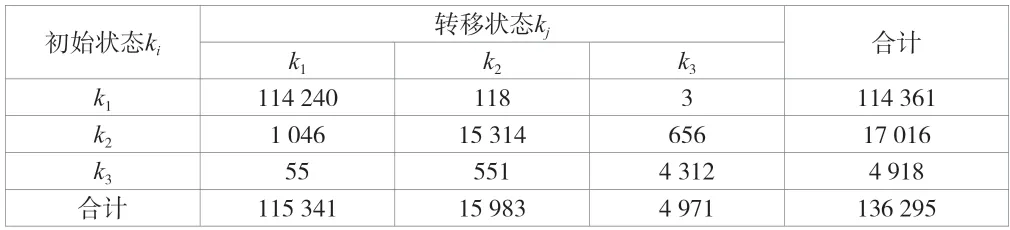
表2 通信模块状态转移数据

由表2可以获得通信模块转态转移概率矩阵，如公式（20）所示。

通信模块状态概率转移矩阵的物理意义为：假设通信模块状态在上一个时间间隔处于状态1，那么在下一个时间间隔有0.990454的概率保持在状态1，有0.007383的概率转移到状态2，有0.006035的概率转移到转态3。

因为每次统计后都会对通信模块进行修复，所以后续运行都为通信完好状态，即每次从状态1开始，如公式（21）所示。

将公式（20）、公式（21）代入公式（9）和公式（11），经过300次矩阵乘法运算，可以快速得到Π（1）-Π（300）的值，利用公式（22）获得每个时间断面解析值与统计值的误差。

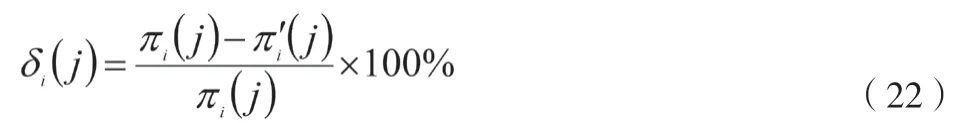
式中：δi（j）为各时间断面解析值与统计值的误差；πi（j）为第j状态的概率。

当i=1，2，3，…，300时，那么20个时间断面的平均误差如公式（23）所示。

利用公式（22）和公式（23）可以求得300个时间断面通信模块状态处于状态1、状态2和状态3的统计值与解析值的平均误差，分别为1.38%、1.06%和12.49%。当通信模块处于状态3时，误差较大的原因为样本数量较少，造成πi'（j）基数较小，从而导致误差较大。利用公式（14）、公式（16）可以求得该算例通信模块的可靠性失效概率为Π（∞）=[0.998403 0.001416 0.000183]，该结果满足智能计量设备寿命不少于5 a的要求，且与统计数据相符。由上述分析可知，由状态转移概率矩阵A和当前通信模块状态直接获得通信模块在下一阶段的失效概率，其预计值在误差范围之内，说明通信模块的通信失效的随机过程具有马尔科夫性。

5 结语

该文对智能计量设备通信模块的运行状态进行分类并得到了3种状态，论证通信模块失效过程具有马尔科夫性，在足够数量的样本的支持下，可以统计出通信模块失效的概率转移矩阵A，由A和当前通信模块状态，可以快速解析获得未来时间段的通信模块失效概率及变化，根据Δt的取值不同，可以将其分别应用于通信模块的运行、检修及规划，同时还可以完成计量设备的周期轮换等工作，从而提升了产品的可靠性。