考虑链与链竞争下的回收再制造供应链决策研究

孙凡松，蹇 明，宋泳萩

（西南交通大学，交通运输与物流学院，成都 611756）

0 引 言

再制造是处理使用后产品的一种良好途径，不仅可以提高生产力和节约资源，还可以解决部分就业问题及给企业带来收益，据报道，美国再制造部门的规模已达到53 亿美元，涉及70 000 多家公司和480 000 名员工[1]。为了更好地实现资源合理利用，我国也为此做了许多努力，如发布了《中国废弃电器电子产品回收处理及综合利用行业白皮书》等[2]。因此，研究回收再制造问题具有现实意义。

关于回收再制造供应链决策问题的研究，He[3]分别探讨了需求确定和不确定时的回收定价与再制造决策问题。Chen 和Chang[4]在需求依赖于价格且新产品和再制造产品之间是部分可替代的情形下，研究了新产品和再制造产品的定价问题。解凤珏等[5]考虑了消费者对新制造产品和再制造产品支付意愿存在差异，且针对零售商主导的两阶段闭环供应链系统研究了供应链成员定价与再制造决策问题。邹宗保等[6]针对由一个供应商、一个制造商和一个第三方再制造商组成的供应链，探索了制造商将再制造业务外包给再制造商对供应链成员决策的影响。刘志等[7]针对高端产品和低端产品的差异化竞争，构建了高端制造商将再制造专利许可作为外部竞争要素情形的闭环供应链竞合决策模型，并分析了消费者异质需求下再制造专利许可对闭环供应链生产决策、利润和环境效益的影响。李国威等[8]基于我国重卡发动机再制造市场特征，研究了汽车生产商绝对主导且再制造产品需求只来自售后服务市场时，再制造产品顾客接受度对原始设备制造商和再制造商决策的影响。闻卉等[9]针对带有零部件和产品两级再制造的S-M 闭环供应链，分别考虑了制造商主导、供应商主导和无市场主导者三种渠道权力结构下的定价决策。何景师[10]则研究了收益共享契约下的闭环供应链回收再制造决策问题。

上述研究均基于单一回收再制造供应链为研究背景，与上述研究不同，本文拓展到了两条供应链，并考虑了链与链之间存在竞争且所生产的两种产品具有替代性。此外，也进一步考虑了再制造成本依赖于回收努力（如保鲜努力[11]等运输条件）的情形。研究了制造商回收努力投入决策、零售商的定价决策及制造商是否应投入回收努力的问题，并分析了消费者的价格敏感性变化对制造商和零售商的决策行为和利润的影响。

1 模型描述与假设

考虑两条回收再制造二级供应链由两个制造商和两个零售商所组成，两制造商负责对两种可替代性产品进行回收再制造加工，然后通过不同的零售商销往同一市场，如图1 所示。假设制造商1、制造商2 回收两种产品的价格分别为常数1c和 c2，在不影响结论的前提下，不失一般性，令其均为0。

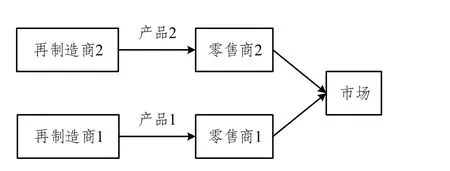
图1 结构示意图

此外，制造商为主导者，零售商为追随者，制造商的批发价格为w。对于两再制造商而言，其投入的回收努力ie （如改善回收运输条件等）越大，i ∈{1,2}，回收产品的损耗度越低及回收质量越好，再制造的成本也会越低，故再制造产品成本可表示为：

式中：m 为无回收努力时的最大再制造成本；b 表示回收努力效率，b 值越大表示制造商投入单位回收努力对降低再制造成本的效果越好。回收努力ei的成本为， ki表示努力成本系数， i∈{1,2}。

同时，再制造产品i 的市场需求 Di与产品i 的零售价格pi负相关，而与再制造产品j 的零售价格pj正相关，故再制造产品的需求函数可表示为：

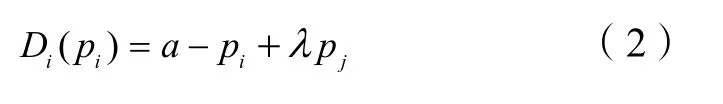
式中：a 为基本市场规模；就产品i 而言，λ 为i链上的消费者对再制造产品j 价格的敏感性系数（需求交叉敏感系数），λ 的值越大表示消费者对再制造产品j 的价格越敏感， i ,j ∈{1,2}，i ≠ j。

2 模型建立

2.1 制造商投入回收努力模型

若制造商对一级市场未销售完的产品在回收的过程中投入了回收努力，则根据上述的模型假设，可以得到制造商1 和制造商2 的利润函数分别为：

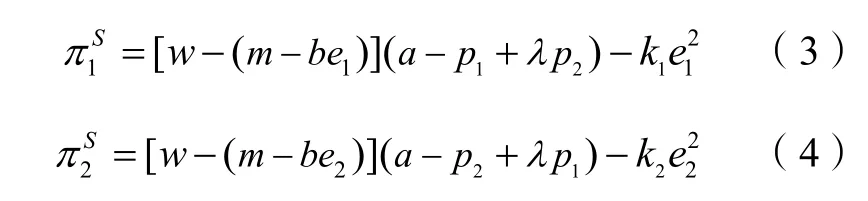
零售商1 和零售商2 的利润函数分别为：

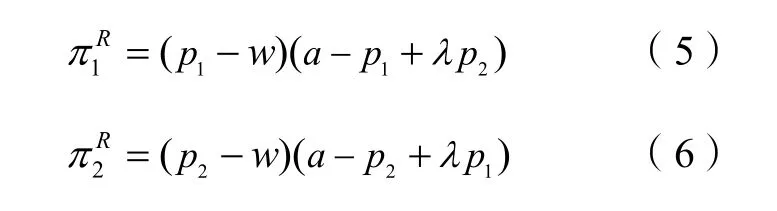
由于两制造商为主导者，两零售商为追随者，因此，供应链的决策顺序为：两零售商首先决定其最优零售价格；两再制造供应商再决定其回收努力水平。接下来，对两零售商的决策行为进行分析。

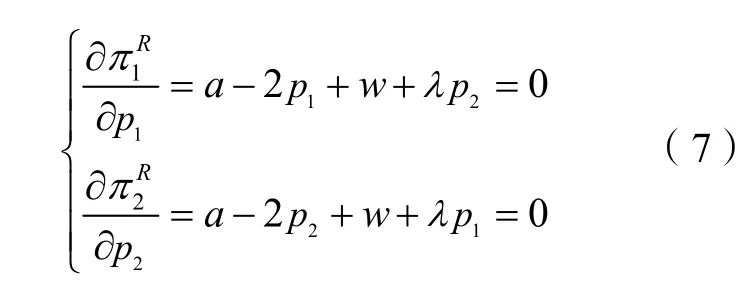
再将式（8）分别代入式（3）和（4），可得：

命题1 在两竞争的供应链中，两制造商和两零售商的最优决策分别为：

再将式（12）～（14）代入式（3）～（6），即可得两制造商和两零售商的最优利润，因此可以得到命题2。

命题2 在两竞争的供应链中，两制造商和两零售商的最优利润分别为：

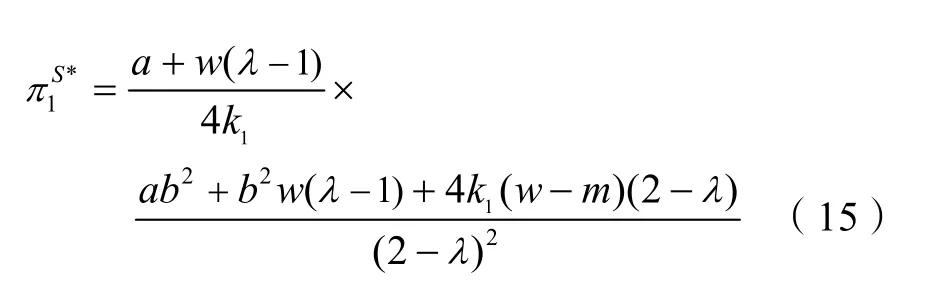
从而，可以得到命题3。

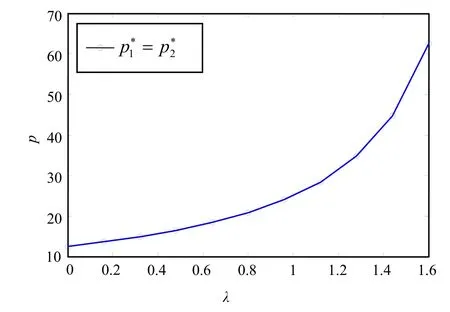
图2 λ 对和的影响

图3 λ 对和的影响

命题4 说明了，就链i 而言，消费者对链j 的零售价格越敏感，制造商i 和零售商i 的利润越大，i ≠ j且i ,j∈{1,2}，如图4 和图5 所示。

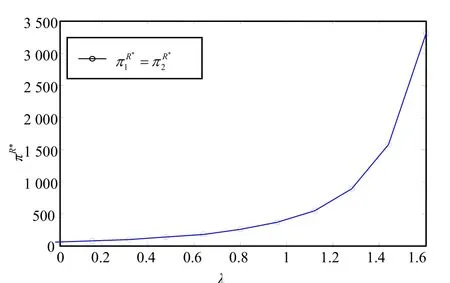
图4 λ 对和的影响

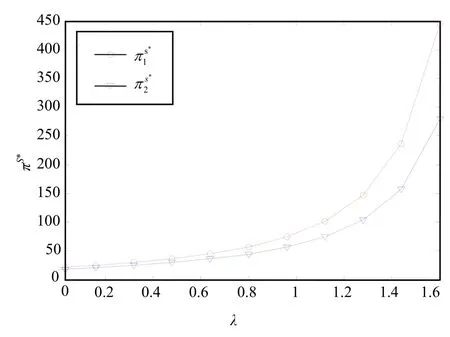
图5 λ 对和的影响

2.2 制造商未投入回收努力模型

若制造商对一级市场未销售完的产品在回收的过程中未投入回收努力，即ei= 0，则制造商1 和制造商2 的再制造成本均为m，此时二者的利润函数分别为：

零售商1 和零售商2 的利润函数分别为：

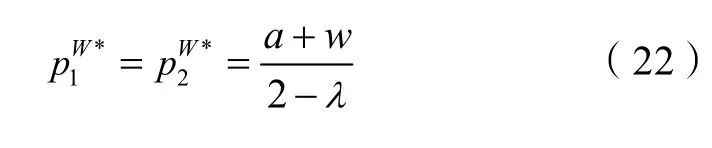
再将式（22）分别代入式（18）～（21），可得：通过以上分析，可以得到命题5。

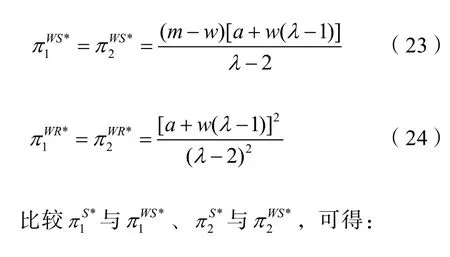
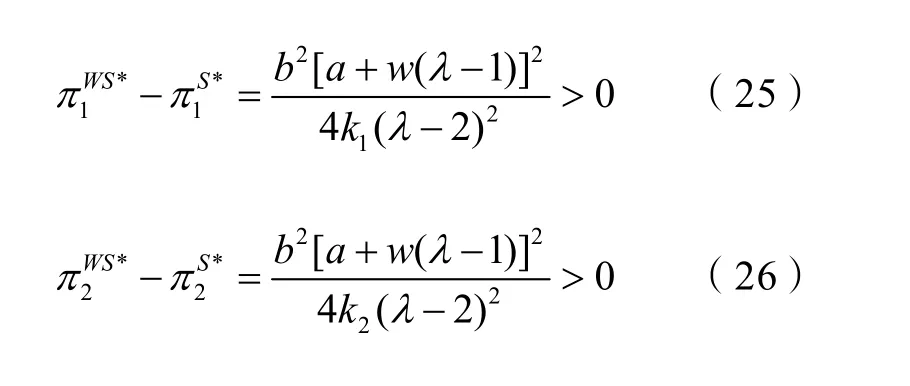
3 结束语

本文考虑了两条竞争性供应链由两个制造商和两个零售商所组成，其中两个制造商对两种具有一定替代性的产品进行回收再制造，然后再通过两个不同的零售商销往市场，且再制造成本与制造商的回收努力负相关。研究了制造投入回收努力模型和不投入回收努力模型下供应链上下游企业的决策问题，探讨了消费者的零售价格敏感性变化对制造商和零售商的决策行为和利润的影响，并对投入回收努力模型和不投入回收努力模型下的制造商利润进行了对比分析。通过全文分析，可以发现：① 竞争性供应链的纳什均衡解唯一；② 若一条链上的消费者对另一条链上的零售价格越敏感，则这条链上制造商的努力水平、零售商的零售价格及二者的利润均越大；③ 较制造商不投入回收努力而言，若制造商选择合适的回收努力投入水平，则可使得两制造商利润实现双赢。