基于抛物线模型的地基沉降计算的切线模量法
2021-06-05杨梓铭
杨 敏,杨梓铭
(同济大学土木工程学院 上海200092)
0 引言
地基变形是地基基础设计的基本要求之一,其中竖向变形即沉降的计算精度依然存在问题。我国现行规范中推荐的分层总和法,作为一种工程实用方法,尚存在一些缺陷:完全侧限的假设与实际情况相差较大;室内试验取样时存在对样本的扰动,使压缩模量测得偏低,而软土等存在触变性更易受到扰动影响;修正沉降计算经验系数ψs的取值范围过大,使用时会有一定的主观性等等。以上缺陷导致地基沉降计算误差不小,设计时难以把握变形控制设计原则。
相比从室内试验获得压缩模量计算沉降,在现场进行的原位试验,可以在对试验土层基本不扰动或少扰动的情况下获得变形参数,同时测定的土体范围大、代表性好。其中平板载荷试验能够模拟建筑物地基在竖直受荷下的工程性能,利用荷载-沉降(P-s)曲线的直线段,得到承压板影响范围内的地基土的变形模量。但是变形模量从定义上仅适用于载荷试验的直线变形阶段,即P-s 呈线性关系的部分。而为了充分发挥地基受荷的潜力,地基承载力常取至发生局部剪切变形,但塑性区范围不超过某一限度的临界荷载,此时P-s呈非线性关系。
在如何利用平板载荷试验的结果得出考虑应力-应变非线性阶段的地基沉降计算方法的问题上,焦五一[1-2]曾提出弦线模量法,杨光华等人[3-10]先后提出了原位土的双曲线模型法、双曲线切线模量法、双曲线割线模量法等实用方法。其主要思路在于将平板载荷实验的P-s 关系用双曲线模型拟合,进而或直接得到P-s 的函数表达式进行沉降计算,或得到等效切线模量、割线模量的方式用分层总和法计算。这类方法的优势在于计算简便,且能反映出应力水平对变形参数的影响,体现了P-s的非线性关系。
然而双曲线模型的数学性质与载荷试验第三阶段的定义略有不符之处:双曲线具有渐近线,也表明其永远取不到上限。反映在平板载荷试验上,即为荷载无法达到极限压力Pu;而理想程度上的载荷试验,是在剪切变形阶段曲线斜率逐渐变大,再到破坏阶段的荷载大于或等于极限压力后,即使荷载不变,沉降也会持续发展或不断增大,始终不能达到稳定标准,即土体进入完全塑性状态。
为解决这一缺陷,本文提出用抛物线模型来拟合P-s曲线的非线性部分。抛物线的数学性质存在明确的可取到的顶点,能对应极限荷载,同时也符合剪切变形阶段斜率不断增大的曲线走势。
1 基于抛物线模型的切线模量法
载荷试验进入剪切变形阶段后,P-s 关系由直线变为曲线,且斜率逐渐增大,当荷载达到极限压力Pu时,即使不增大荷载沉降也会一直发展,意味着理想化的P-s关系再度变为直线,并垂直于P轴,即土体达到完全塑性状态。
对此,剪切变形阶段的P-s 曲线可采用有明确极大值的函数进行拟合。本文采用基于抛物线模型的二次函数的拟合方式,预设二次函数:
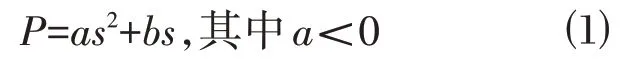
对式⑴求反函数得
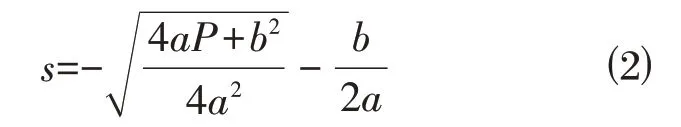
再求导,得

代入最大值Pu

令二次函数在原点处斜率为k0,即b=k0

式中:I0为压板位于半空间表面的影响系数;I1为承压板在一定埋深时的修正系数;μ为土的泊松比;d为圆形承压板的直径或方形承压板的边长;Et0为初始切线模量。
在直线变形阶段由各向同性弹性半空间理论可求解土体变形模量,令等效切线模量

令

得

将式⑷、式⑹代入式⑼,得

其中P/Pu代表了应力水平对等效切线模量的影响。实际工程中荷载可能未必加载到破坏荷载,故引入破坏比系数Rf,式⑽改为
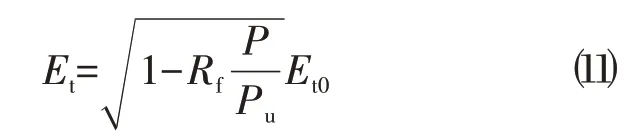
得到切线模量后,再采用增量法,每一层的沉降量为:
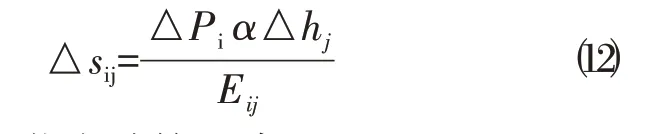
进行逐级加荷来计算沉降。
2 案例检验
通过广州市某大厦的筏板基础[4,10]来验证基于抛物线模型的切线模量法的有效性。
广州市某大厦的典型地质剖面如图1 所示,基础底面约在地面以下12 m深处,基底土层为粉质粘土层(Qel),标贯击数N=11~20 击,压缩模量Es1-2=4.3 MPa,而平板载荷试验求得的变形模量为40 MPa,大约为压缩模量的10 倍。而由弹性理论得到变形模量与压缩模量的关系为
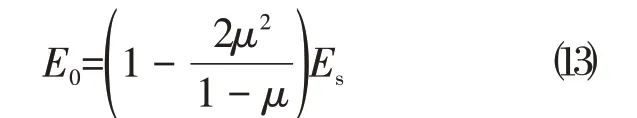
即变形模量应该小于压缩模量,但实际结果则相反,这反映出原状土的试验参数与室内试验结果会出现差异很大的情况,尤其是压缩试验的土样受扰动影响很大。如果采用室内压缩实验的压缩模量进行沉降计算,结果会明显偏大,很难设计成筏板基础。

图1 广州某大厦典型地质剖面Fig.1 Typical Geological Section of a Building in Guangzhou
在基础基底面处进行的一次载荷试验所得的Ps曲线(直径D=80 cm的圆形载荷板)如图2⒜所示。
对式⑴转换得

对试验P-s曲线进行拟合,P/s-s关系如图2⒝所示。

图2 试验P-s及P/s-s曲线[4]Fig.2 P-s Curve and P/s-s curve of Test[4]
求得a=-4.328 6,b=106.12,Pu=650 kPa,Et0=60.6 MPa。P-s曲线计算与实测比较如图3所示。
根据太沙基地基极限承载力公式
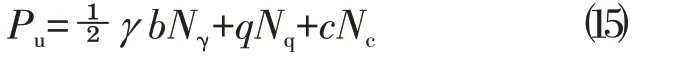
因未提供c、φ 数值,可假设φ 值来反求c 值。这里假定φ =20°,Nγ=4.00,Nq=7.42,Nc=17.60,b=0.8 m,γ=20 kN/m3,q=0。代入太沙基地基极限承载力公式,求得c=35.1 kPa。

图3 P-s曲线计算与实测比较Fig.3 P-s Curve Calculation and Actual Measurement Comparison
采用以上的切线模量法和所求得的有关参数,基础面积近似按40 m×40 m 正方形考虑,实际基底应力按每层15 kPa,共14 层考虑,则按P=210 kPa 试算沉降,按分层总和法计算,分层厚度按2 m 考虑,荷载增量分级取△P=15 kPa,计算深度至基础底以下20 m,20 m 以下为强风化岩面,岩层的沉降不计。逐级加荷计算得沉降结果,如表1所示。

表1 逐级加荷算得沉降[4]Tab.1 Computed Settlements under Incremental-load
抛物线切线模量法及使用压缩模量计算[4]的沉降计算结果分别为28.53 mm 和774.40 mm,实测平均沉降[4]为40.00 mm。
可见相对于使用压缩模量计算得到的沉降结果,使用基于抛物线模型的切线模量法更接近实测沉降,通过新方法计算可以论证设计成筏板基础是可行的。同时也注意到本案例中新方法的计算结果偏于危险,需要更多的案例积累经验。
3 结论
利用原状土的试验参数进行地基沉降计算,能较好地解决室内试验取样时对土体扰动的问题。本文提出的抛物线切线模量法,在原有的双曲线切线模量法上进行改进,更符合理想载荷试验曲线的特性,并保留了体现模量受应力水平影响的特点。之后可根据更多的实际沉降案例,进一步检验精度并积累经验,使之用于解决地基沉降的计算问题。
