基于混合回归分析的荷斯坦奶牛氮排泄量预测
2021-06-05董瑞兰孙国强于光辉
董瑞兰 孙国强 于光辉
(青岛农业大学动物科技学院,青岛 266109)
畜牧养殖对环境造成的污染问题已引起全球的广泛关注[1]。奶牛氮排泄量与饲粮的粗蛋白质(CP)含量和消化率密切相关[2]。在奶业生产中,为了提高产奶量和乳品质而提高饲粮CP的含量,导致70%~80%的摄入氮通过粪便和尿液排泄到水体、陆地和大气中[3-4],进一步造成环境的恶化。我国农业农村部开展的全国农业污染源普查中,畜禽养殖污染物的排放是基于动物的产排污系数核算的[5]。这种方法操作起来方便,但是粪污养分含量随饲料的来源和组成不同而发生变化,用固定的系数估计变化的排放数值是不准确的。因此,通过影响氮排泄量的指标开发预测模型是准确评估养分排放的有效方法[6],有助于提高粪污养分预测的准确性。而且,鉴于尿液中含有的氮比粪中的氮更易挥发[7],通过排泄路径(尿液和粪便)预测氮排放量更有意义。
关于奶牛的氮排泄量已有较多预测方程报道,有根据乳中尿素氮(milk urea nitrogen,MUN)[8-9]、氮摄入量(nitrogen intake,NI)[10-12]、瘤胃降解蛋白(rumen degradable protein,RDP)[13]预测尿氮(urinary nitrogen,UN)的一元线性方程;也有根据NI、干物质采食量(dry matter intake,DMI)和产奶量(milk yield,MY)组合[14],或MUN、CP和DMI组合[15]预测UN的多元线性方程。有根据NI[10-11]或DMI[12]预测粪氮(fecal nitrogen,FN)的一元线性方程;也有根据NI和DMI[14]或有机物采食量(organic matter intake,OMI)组合[16-17]预测FN的二元方程。总氮(total nitrogen,TN)可根据MY[13]或NI[11-12,18]单独预测或根据NI和DMI组合[14],体重(body weight,BW)、CP与MY组合[18]以及BW、CP与DMI组合[19]预测。Dong等[20]用荷斯坦奶牛数据库评估了上述预测模型,发现预测的准确性普遍偏低。因此,本研究旨在用荷斯坦奶牛的氮排泄数据库,构建准确的UN和FN预测模型,并验证准确性,为奶牛生产提供依据。
1 材料与方法
1.1 建立数据库
荷斯坦奶牛氮排泄数据库(包括32个发表研究的99个观察值)来自Dong等[20]。采用文献发表的荷斯坦奶牛氮排泄数据构建数据库。在线检索的数据库包括中国知网(CNKI,http://www.cnki.net/)、Science Direct(http://www.sciencedirect.com/)和Journal of Dairy Science(http://www.journalofdairyscience.org/)。确立相关文献研究的标准是:1)研究对象是荷斯坦奶牛;2)从已出版文献的数据库检索出在中国进行的研究,代表现代奶牛养殖的实际条件,特点是使用全混合日粮(TMR)饲养和采用自动挤奶设备;3)需提供荷斯坦奶牛氮排泄的输出变量信息,包括UN、FN、MUN、TN和尿氮占总氮的比例(UN/TN);4)需提供关于饲粮的CP含量、奶牛的NI、DMI、BW和MY及乳成分等特征输入变量信息;5)若研究中某些变量未报道,但可通过其他已知变量计算的也包括在数据库中。例如,饲粮的CP含量可通过DMI和NI计算获得,TN为UN与FN的总和,UN/TN为UN与TN的比值。剔除观察值变量缺失的5个研究[21-25],剩余27个研究的89个观察值对应的所有变量均已知,即如果文献的观察值提供了关于NI、DMI、CP、BW、粗饲料比例(forage proportion,FP)、MY、乳氮(milk nitrogen,MN)、MUN、氮的全消化道表观消化率(apparent total tract nitrogen digestibility,TTND)、乳氮占氮摄入量的比例(MN/NI)、氮摄入量占干物质采食量的比例(NI/DMI)、饲料利用效率(feed efficiency,FE,MY与DMI的比值)、氮沉积量(nitrogen retention,NR)、UN、FN、TN、UN/TN等所有变量信息,则被包含在数据库中。如果有观察值的某个变量未知则不被包含在数据库中。
数据库经JMP统计软件马氏离群分析(Mahalanobis outlier analysis,MOA)认定为极值的数据,其学生化残差在-2.5~2.5的范围之外,被鉴定为离群异常值。通过分析,共计8个观察值被鉴定为离群异常值,剔除离群异常值后,最后剩余27个研究的81个观察值(随机选择2/3数据用于建模,1/3数据用于分析模型预测值与实际观察值之间的回归关系)进行最终的分析。
1.2 构建预测模型
1.2.1 筛选最佳预测变量
模型的最佳预测变量采用SAS 8.1软件Corr过程程序的皮尔森相关系数(r)确定[1]。依次分析输入变量(NI、DMI、CP、MUN、BW、TTND、NI/DMI、MY、MN、MN/NI、FP、NR、FE)与输出变量(UN、FN、TN、UN/TN)之间的相关关系。
1.2.2 自变量和因变量之间的回归关系
经1.2.1中筛选出的最佳预测变量作为自变量,将奶牛的氮排泄量(UN、FN、TN、UN/TN)作为因变量,分析自变量和因变量之间的一元和多元回归关系。
进行多元回归关系统计分析时,采用逐步回归分析法(step wise selection,SWS)剔除不显著(P>0.05)的变量,筛选出最终保留在模型中的自变量。多个变量之间的共线性用方差膨胀因子(variance inflation factors,VIF)检验,它是衡量每个自变量与模型中其他变量之间紧密相关的指标。预测变量若具有较大的VIF(>2.5),可导致模型发生较大的膨胀误差。当确定存在共线性时,预测氮排放量时皮尔森相关系数最小的变量即被剔除。
1.2.2.1 一元线性模型
自变量和因变量之间的一元回归关系用以下方程分析:
y=bx+a。
式中:x指因变量;y指UN(g/d)、FN(g/d)、TN(g/d)和UN/TN;a是固定常数;b指对应变量的系数。
1.2.2.2 多元线性模型
自变量和因变量之间的多元回归关系用以下方程分析:
y=b1(x1)+b2(x2)+b3(x3)+…+bn(xn)+a。
式中:x指因变量;y指UN(g/d)、FN(g/d)、TN(g/d)和UN/TN;a是固定常数;b1,b2,b3,…,bn指各对应变量的系数。
1.2.3 模型的拟合效果
用SAS 8.1软件分析均方根误差(root mean square error,RMSE)和阿凯克信息论准则(Akaike’s information criterion,AIC)值。RMSE和AIC值是模型拟合好坏的指标,其值越小代表模型拟合效果越好[1]。
1.3 模型预测值与实际观察值之间的回归关系分析
将模型输出的预测值作为自变量,实际观察值作为因变量,绘图分析模型预测值与实际观察值之间线性回归关系的显著性,获得决定系数(R2),同时确定回归线和等线(y=x)的偏离程度。
1.4 数据的统计与分析
用SAS 8.1软件的混合回归模型(mixed regression model,MRM)过程程序分析自变量和因变量之间的一元和多元回归关系,P<0.05为回归关系显著,P<0.01为回归关系极显著。通常认为,模型预测值与实际观察值之间R2越大,则获得的预测模型越准确。在用SAS 8.1软件程序分析时,不同的研究作为随机变量也包括在模型中,用于消除不同研究之间的试验误差。模型预测值和实际观察值之间的线性关系用以下方程分析:
y=bx+a。
式中:x指UN(g/d)、FN(g/d)、TN(g/d)和UN/TN的模型预测值;y指UN(g/d)、FN(g/d)、TN(g/d)和UN/TN的实际观察值;a是固定常数;b指对应变量的系数。
2 结果与分析
2.1 建模数据库
由表1可知,奶牛的BW、CP、DMI、TTND、NI平均值分别为565 kg、15.4%、19.20 kg/d、69.8%和470 g/d,变动范围分别为407~755 kg、11.0%~19.2%、11.57~28.10 kg/d、58.9%~78.0%和214~720 g/d。奶牛的UN和FN的变动范围较大,介于58.2~329.0 g/d、81.0~193.0 g/d,平均值分别为168.0和141.0 g/d。奶牛的TN变动范围为139.2~481.3 g/d。UN/TN平均值为0.54,变动范围为0.39~0.69。

表1 基于动物和饲粮因子以及氮输入和输出变量的建模数据库描述性统计
2.2 奶牛氮排泄量与动物和饲粮因子之间的皮尔森相关系数
由表2可知,UN分别与NI、DMI、CP、MUN、TTND、NI/DMI、MY和MN呈显著或极显著正相关关系(P<0.05或P<0.01)。FN分别与NI、DMI、CP、NI/DMI、MY、MN和FE呈极显著正相关关系(P<0.01),而与TTND和FP呈显著或极显著负相关关系(P<0.05或P<0.01)。TN分别与NI、DMI、CP、MUN、NI/DMI、MY和MN呈极显著正相关关系(P<0.01)。UN/TN分别与DMI、MUN、TTND和FP呈显著或极显著正相关关系(P<0.05或P<0.01),而与NR呈极显著负相关关系(P<0.01)。
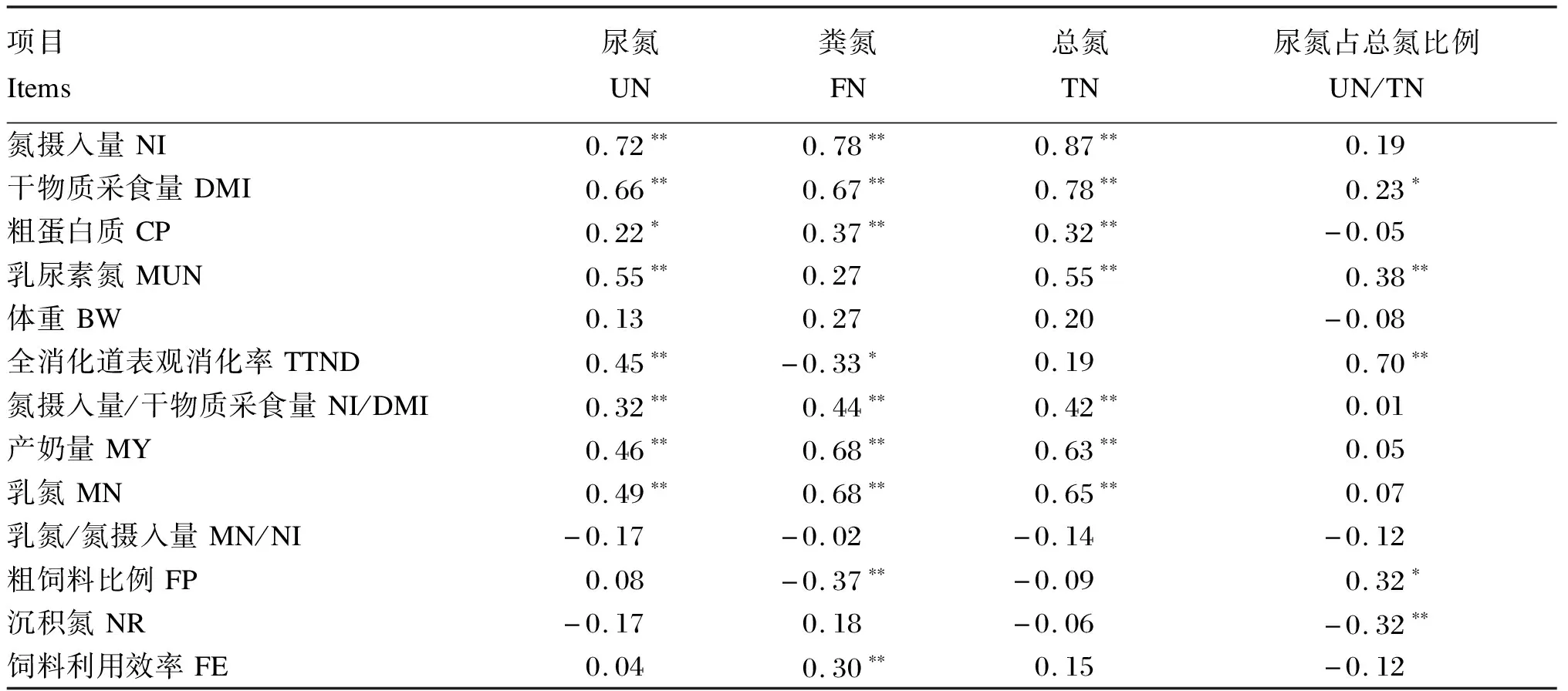
表2 奶牛氮排泄量与动物和饲粮因子之间的皮尔森相关系数
2.3 一元线性预测模型
2.3.1 UN预测模型
预测UN的模型见表3(模型1~6)。输入变量NI、CP、NI/DMI、MY、MN/NI、MN对回归关系都有显著影响(P<0.05)。根据RMSE和AIC值可知,基于单一变量的UN模型拟合效果为:MN/NI 表3 奶牛尿氮、粪氮和总氮的一元线性预测模型 2.3.2 FN预测模型 预测FN的模型见表3(模型7~12)。输入变量NI、MY、MN、DMI、NI/DMI、CP对回归关系都有显著影响(P<0.05)。当单独用NI(模型7)预测FN时,其RMSE和AIC值最低。但单独用CP(模型12)预测FN时,其RMSE和AIC值最高。用NI预测的FN与实际观察值之间的比较见图1-b,回归分析显示,基于NI的回归模型预测值和实际观察值之间的R2为0.84(P<0.01)。 2.3.3 TN预测模型 预测TN的模型见表3(模型13~18)。输入变量NI、MY、MN、NI/DMI、CP、FP对回归关系都有显著影响(P<0.05)。当单独用NI(模型13)预测TN时,其RMSE和AIC值最低。但单独用FP(模型18)预测FN时,其RMSE和AIC值最高。用NI预测的TN与实际观察值之间的比较见图1-c,回归分析显示,基于NI的回归模型预测值和实际观察值之间的R2为0.93(P<0.01)。 图1 尿氮(a)、粪氮(b)、总氮(c)和尿氮占总氮的比例(d)的实际观察值和模型预测值之间的关系 2.3.4 UN/TN预测模型 UN/TN预测模型见表3(模型19~22)。输入变量TTND、MN/NI、CP、FE对回归关系都有显著影响(P<0.05)。当单独用TTND(模型19)预测UN/TN时,其RMSE和AIC值最低。单独用TTND预测的UN/TN与实际观察值之间的比较见图1-d,回归分析显示,基于TTND的回归模型预测值和实际观察值之间的R2为0.90(P<0.01)。 2.4.1 UN预测模型 预测UN的多元线性回归模型见表4(模型23和24)。在多个输入变量中,CP、DMI与NI/DMI组合以及DMI与NI/DMI组合对UN多元线性模型有极显著影响(P<0.01)。模型23的RMSE和AIC值与模型24相比较低。用模型23预测的UN与实际观察值之间的比较见图2-a,回归分析表明,模型23的预测值和实际观察值之间的R2为0.90(P<0.01)。 表4 奶牛尿氮、粪氮和总氮的多元线性预测模型 2.4.2 FN预测模型 预测FN的多元线性回归模型见表4(模型25和26),在多个输入变量中,MY与NI组合以及MY与DMI、FP组合对FN多元线性模型有极显著影响(P<0.01)。模型25的RMSE和AIC值较模型26低。用模型25预测的FN与其实际观察值之间的比较见图2-b,回归分析表明,模型25的预测值和实际观察值之间的R2为0.87(P<0.01)。 图2 尿氮(a)、粪氮(b)、总氮(c)和尿氮占总氮的比例(d)的实际观察值和模型预测值之间的关系 2.4.3 TN预测模型 预测TN的多元线性回归模型见表4(模型27~29),在多个输入变量中,NI与NI/DMI组合、DMI与NI/DMI组合以及DMI与MY组合对TN多元线性模型有极显著影响(P<0.01)。模型27的AIC和RMSE值是3个TN预测模型中最低的。模型29的AIC和RMSE值是3个TN预测模型中最高的。用模型27预测的TN与其实际观察值之间的比较见图2-c,回归分析显示,模型27的预测值和实际观察值之间的R2为0.92(P<0.01)。 2.4.4 UN/TN预测模型 预测UN/TN的多元线性回归模型见表4(模型30和31)。NI、TTND、FP与NR组合以及NI、TTND与NR组合对UN/TN多元线性模型有极显著影响(P<0.01)。模型31的RMSE和AIC值最低。用模型31预测的UN/TN与实际观察值之间的比较见图2-d,回归分析显示,模型31的预测值和实际观察值之间的R2为0.89(P<0.01)。 数据库涵盖了奶牛泌乳初期、中期和后期各产乳阶段。但需指出的是,由于研究使用了发表文献数据,收集的数据是各试验处理的观察值平均值,而不是动物个体的试验数据,所以本研究未考虑动物之间的个体差异。与美国1990—1995年泌乳奶牛数据库[12]DMI范围10.3~28.2 kg/d相比,荷斯坦奶牛的最低和最高DMI数值与之接近。将荷斯坦奶牛的氮排泄数据库与Spek等[15]建立的北欧和北美数据库相比,中国NI的平均值低于北欧(470 g/d vs. 485 g/d)和北美(470 g/d vs. 637 g/d)。同样,UN的平均值也低于北欧(168 g/d vs. 185 g/d)和北美(168 g/d vs. 212 g/d);FN的平均值也低于北欧(141 g/d vs. 159 g/d)和北美(141 g/d vs. 223 g/d)。 用单一变量预测UN时,基于NI(模型1)预测的准确性(AIC值=510.2,R2=0.91)最高。关于NI和UN之间存在显著的相关关系已有较多报道[10-12]。Castillo等[10]和Kebreab等[11]研究发现,NI和UN之间呈指数关系,原因可能为在氮平衡为正的情况下,UN不是直接测定,而是用物料守恒法计算差值获得,由此导致了UN的偏高估计。荷斯坦奶牛排泄的UN与NI之间呈现正相关线性关系,而且用NI可准确预测奶牛的UN,该结果与Kebreab等[11]和Reed等[12]的结论一致。本研究中UN和NI之间的回归关系斜率与Reed等[12](0.34 vs. 0.33)和Kebreab等[11](0.34 vs. 0.38)报道的范围接近,而且本研究的回归关系常数项值更低(4.8 vs. 12.0和4.8 vs. 20.0)。 当用多个变量预测UN时,模型23提供了较好的预测方法(R2=0.90)。Spek等[15]用DMI和CP对欧洲和北美奶牛的UN进行预测,发现在输入变量DMI和CP的基础上增加第3个变量MUN,比单独用MUN或CP以及同时用MUN和CP的组合预测得更准确。本研究中,模型23的回归关系常数项与Spek等[15]报道的一致,而且AIC值更低(488.3 vs. 988.0)。 用单一变量NI、MY、MN、DMI、NI/DMI、CP预测FN时,模型7的拟合效果和准确性最高。Castillo等[10]基于英国的奶牛数据发现,FN与NI存在线性函数关系(FN=0.21NI+52.3)。此方程的斜率与本研究的模型7一致,但是Castillo等[10]建立的模型的常数项值约为本研究中模型7的1.2倍。Vasconcelos等[26]也报道了奶牛FN与NI之间存在线性关系。Kebreab等[11]报道了奶牛FN与NI之间也存在类似的线性关系,但FN的斜率为0.28,截距数值为10。Schuba等[27]研究发现NI和FN之间呈二次关系,即FN=117.3+3.24×NI2-0.004 3×NI,但其AIC值高达1 509,说明FN和NI之间二次关系拟合效果低。 用多个变量预测荷斯坦奶牛排泄的FN时,基于NI和MY的FN预测模型(模型25)拟合性略高,预测效果较好(R2=0.87)。将多元线性模型(模型25)与一元线性模型(模型7)相比,发现多元线性模型的预测值和实际观察值之间的R2较高,而常数项值也低于一元线性模型。 将NI、CP、MY、MN、FP与NI/DMI作为单一输入变量时,基于NI(模型13)预测TN的准确性最高(AIC值=505.6,R2=0.93)。用多个变量预测TN时,模型27预测的准确性较高。将基于NI的TN预测模型(模型13)分别与基于NI的UN预测模型(模型1)和基于NI的FN预测模型(模型7)相比,模型13的拟合效果优于模型1和模型7。 考虑到UN在TN中占较大比例,建立了UN/TN预测模型。与MN/NI(AIC值=-157.2,模型20)、CP(AIC值=-139.8,模型21)或FE(AIC值=-148.3,模型22)相比,将TTND(AIC值=-158.0,模型19)作为单一输入变量的模型预测效果最好。通过UN/TN与动物或饲粮因子的多变量回归关系及逐步回归分析发现,变量TTND与UN/TN的相关系数最高。因此,TTND被证明是预测奶牛UN/TN的最佳预测变量,该发现与在肉牛中[1]的研究结果一致。Huhtanen等[14]将CP作为奶牛UN/TN的预测变量,发现二者存在显著的线性关系。但本研究结果发现用TTND预测UN/TN比CP效果更好,原因是TTND与CP密切相关。饲粮CP和氮的消化率越高,就会导致越多的氮以瘤胃氨或小肠氨基酸的形式被吸收。那么,超过奶牛营养需要的剩余氮量就会进入尿液,从而增加了UN的比例。需要注意的是,本研究仅基于发表文献进行建模分析,最好通过试验获得数据进一步验证其预测性。 ① 基于NI的一元UN、FN和TN回归模型以及基于TNND的一元UN/TN回归模型的RMSE和AIC值最低,一元回归模型拟合效果好。 ② 基于DMI、CP与NI/DMI组合的多元UN回归模型,基于NI与MY组合的多元FN回归模型,基于NI与NI/DMI组合的多元TN回归模型的拟合效果好。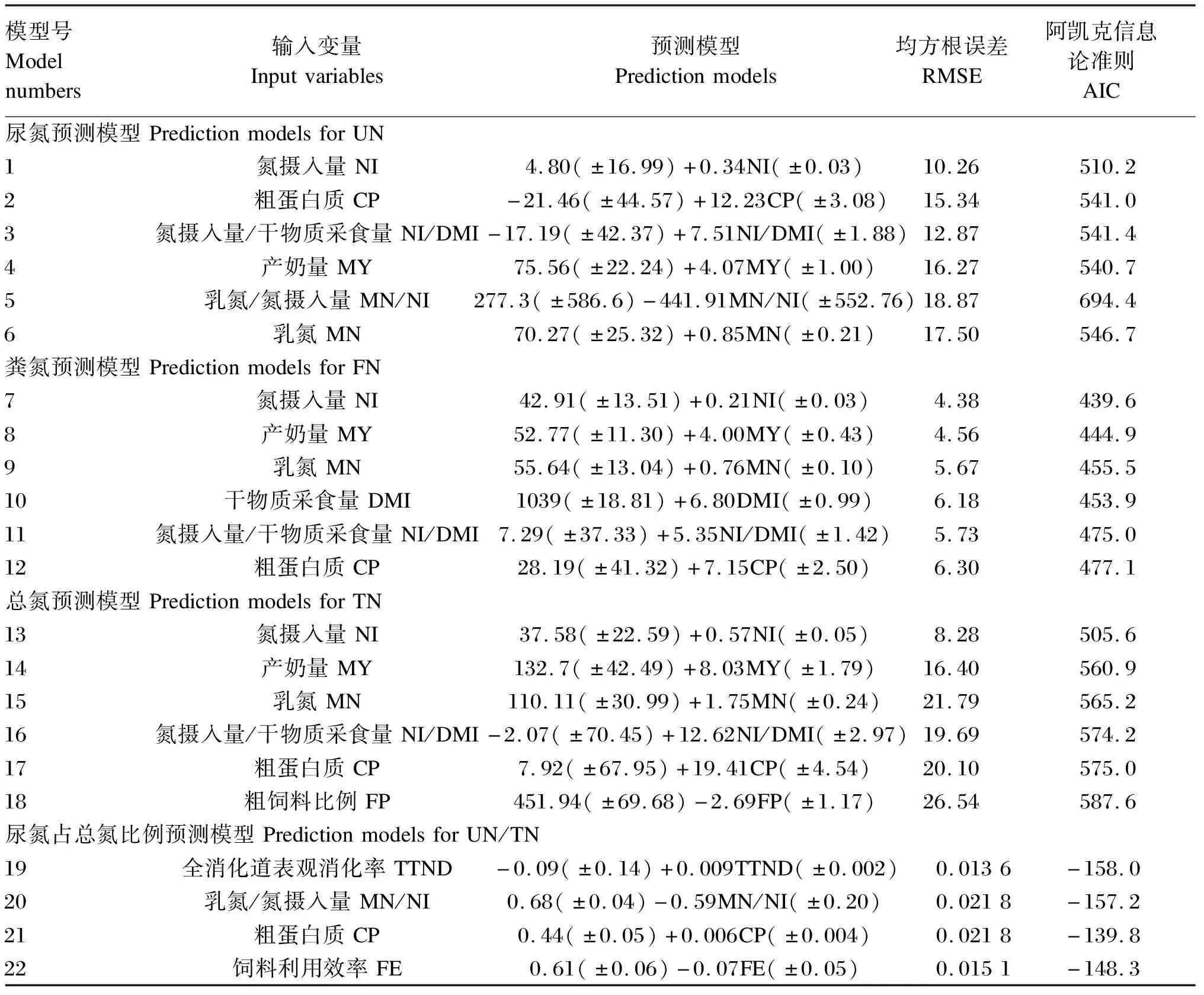

2.4 多元线性模型
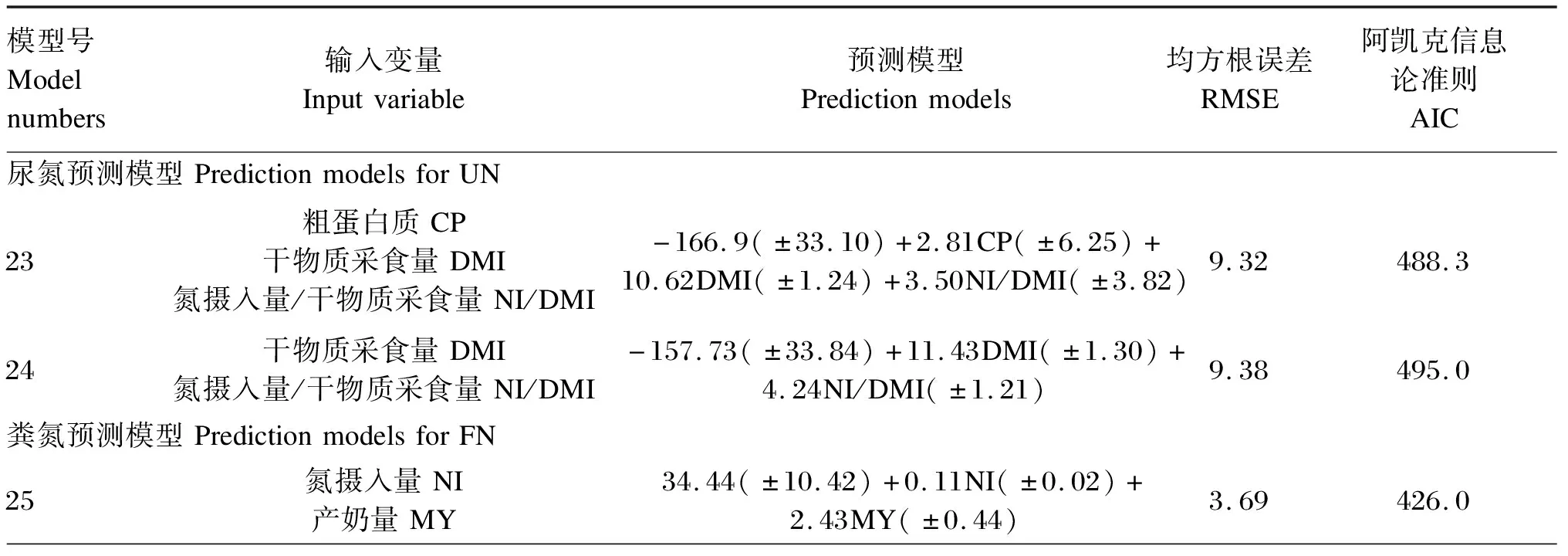

3 讨 论
3.1 建模数据库
3.2 UN预测模型
3.3 FN预测模型
3.4 TN预测模型
3.5 UN/TN预测模型
4 结 论
