非理想电网下的改进型DSOGI-PLL 电压同步检测方法

2021-06-05王德民田福海曲其飞

山东煤炭科技 2021年5期

王德民田福海曲其飞

（1.山东东山王楼煤矿有限公司，山东济宁 272000；2.山东省特种设备检验研究院聊城分院，山东聊城 252000）

电能作为我国重要能源，随着需求量的增长，对电能质量也提出更高要求。大量非线性负载应用的同时，也产生大量谐波。有源电力滤波器（APF）因响应快、精度高等优点，被大量使用[1]。APF 工作中需用锁相环（PLL）获取电压信号[2]。随着日趋复杂的电网工况，APF 对锁相环稳定、精确性等方面做出更高要求。由于PLL 在三相不平衡、直流偏置、频率波动和谐波污染等工况下存在误差，故对PLL 的改进极为必要。

近年来，对PLL 的研究大多基于SRF-PLL 和DSOGI- PLL。文献[3]指出SRF-PLL 在网侧电压畸变和含有负序分量时，检测存在一定的误差。文献[4]通过构造正弦幅值积分器来提取直流分量，减小了直流对DSOGI-PLL 影响，但仍有谐波干扰误差。本文基于DSOGI-PLL，研究了一种可用于非理想电网下的改进型DSOGI-PLL。

1 DSOGI-PLL

SOGI-QSG 作为DSOGI-PLL 的核心部分，其传递函数如下所示：

由式（1）可计算得出系统的相频特性以及幅频特性：

根据式（2）、式（3）可得出，输出电压u'和qu'的相位相差90°。并且，当网侧输入电压的角频率ω=ωr时，输出电压u'可对输入电压实现准确跟踪，即能达到对输入信号精准提取的目的。

DSOGI-PLL 通过设置SOGI-QSG 的谐振频率，实现对基波电压的正交分相，之后计算得出电压正、负序分量。再由SRF-PLL模块将正序分量Park变换，由两相静止坐标系变换到dq同步旋转坐标系，通过PI 控制使分量q 轴电压分量趋于0，最终完成锁相。

2 改进型的DSOGI-PLL

2.1 频率自适应环节

当电网频率变化时，输入频率与DSOGI 谐振频率不等，两者之间存在的差值会造成PLL 输出相有误差。因此，需加入频率自适应环节，实时修正DSOGI 的谐振频率，实现频率自适应。

如图1 所示，uα、uβ分别为两组SOGI-QSG模块的输入，uα′、quα′、uβ′quβ′分别为两组SOGIQSG 的输出，ω0为该环节的输出角频率。将ω0作为SOGI-QSG 模块的谐振频率。

图1 频率自适应环节

定义输入信号uα、uβ：

根据式（2）、式（3）可得出：

由图3 可得出，输出的角频率表达式为：

将式（4）、式（5）和式（6）带入式（7）可得出：

将式（8）变为线性时不变的系统，如下所示：

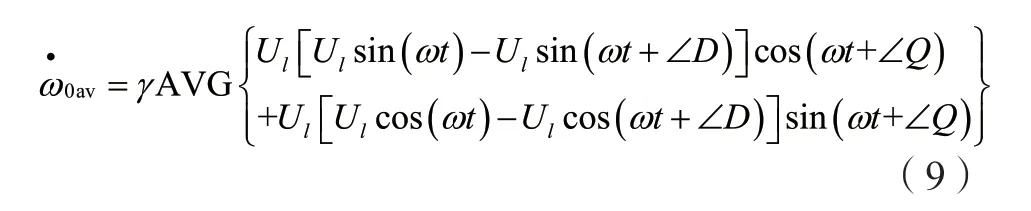
式（9）中，函数f（t，x，ωav）在周期2π/ωav内的平均值即为AVG[f（t，x，ωav）]。将式（9）经过化简得到式（10）：

带入式（2）中的∠D 到式（10），则当ω0→ω 时，式（10）可近似看为：

根据式（11）分析可知，频率自适应环节时间常数的大小与参数γ、阻尼系数k、电网输入电压幅值以及输入频率有关联。当输入频率变化时，因有频率自适应环节的存在，实现频率动态调节和保持恒定。

2.2 基于级联型SOGI-QSG 的DSOGI-PLL 改进方法

在电网实际运行中，系统中还存在大量直流分量。由式（1）可得，Q（s）具有低通特性，对于直流偏置问题较为敏感，这将使qu'存在较大的误差，无法同u'严格正交。由于SOGI-QSG 内含有一个二阶陷波器的结构，其传函表达式如下所示：

式中：εu为u 与u'之间的误差信号。

根据式（12）分析可得，若输入电压u 中除频率为ωr的交流量外，还包含直流量，此时误差信号εu中则会包含全部的直流分量。

因此，本文在SOGI-QSG 中增添一个求差节点，通过kεu抵消掉输出信号qu'中存在的直流偏移量，且将频率自适应环节输出的角频率ω0作为该改进结构的谐振频率。改进的SOGI-QSG 结构如图2。

图2 改进的SOGI-QSG 结构图

此外，为进一步优化DSOGI-PLL 在复杂工作环境下的适应能力，本文提出一种级联型DSOGI，通过前级传统的SOGI-QSG 对输入电压进行初次滤波，快速降低输出分量波形的畸变程度，为后级SOGIQSG 提供更良好的输入。此外，前级传统SOGIQSG 中的输入、输出信号通过频率自适应环节，将得到的网侧实际频率传输给后级改进的SOGIQSG，作为其谐振频率，继而实现频率的实时修正，削弱了系统频率跳变对PLL 频率输出的影响。

综上所述，非理想电网条件下的改进型DSOGI-PLL 电压同步检测方法整体结构图如图3。三相电压经Clarke 变换到两相静止坐标系后，通过级联型DSOGI（CDSOGI）模块实现对谐波分量以及直流分量的滤除，并且将频率自适应环节中的输出频率信号作为级联型SOGI-QSG 中后级SOGIQSG 的谐振频率，达到了对网侧电压频率精准跟踪的目的。之后，正/负序电压分量计算模块计算得出正序分量，由SRF-PLL 模块将其经Park 变换到同步旋转坐标系下，通过PI 控制使分量uq+趋于0，完成锁相。

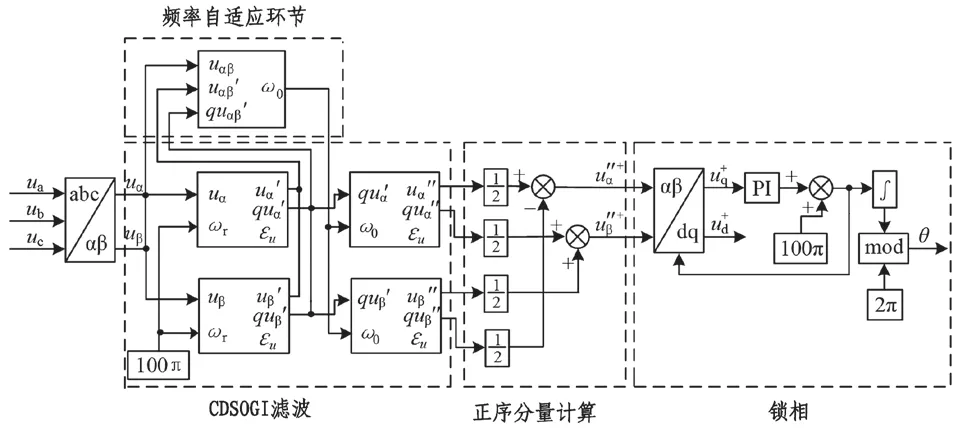
图3 改进型DSOGI-PLL 电压同步检测方法结构图

3 研究效果

利用MATLAB 验证所提方法的实践效果，在网侧电压骤降、谐波污染、直流偏移和频率跳变四种工况下分别进行验证，并与改进前DSOGI-PLL锁相效果对比。

图4 为电压下降且加入谐波的实验结果，t=0.25 s 时，单相电压下降，并在t=0.37 s 时，向系统注入谐波。对比分析可知，t=0.25～0.37 s 期间，系统出现单相电压下降，改进型DSOGI-PLL 与DSOGIPLL 对此均显现出较高的精度。t=0.37～0.55 s 期间，电压下降的基础上又加入高次谐波，此时，本文提出的改进方法对谐波具有更好的抑制作用。

图5 为在电压下降且有直流分量的实验结果。t=0.25 s 时，a 相电压下降，t=0.37 s 时，b 相电压加入直流成分。对比分析可得，在直流作用下，DSOGI-PLL 中包含些许直流分量尚未滤除，而本文提出的改进型DSOGI-PLL 由于加入了求差节点，直流偏移量对其的扰动可基本忽略。

图6 为电压下降且有频率变动的实验结果，t=0.25 s 时，a 相电压下降，t=0.37 s 时，系统频率变为45 Hz。通过频率波形对比分析可得，DSOGIPLL 所得结果有±1 Hz 左右的误差，文中所提改进型DSOGI-PLL 因有频率自适应环节的存在将所测频率误差控制在±0.2 Hz 内。