一类Schrödinger-Maxwell系统解的存在性
2021-06-04杨国翠周见文段胜忠
杨国翠,周见文,段胜忠**
(1.保山学院 数学学院,云南 保山678000;2.云南大学数学与统计学院,云南 昆明650500)
考虑如下的Schrödinger-Maxwell系统:

其中λ >0 为常数.
近年来,对Schrödinger-Maxwell系统及相关系统解的存在性与多解性问题的研究受到学者们的普遍关注[1-10].系统(1)作为一个数理方程,有着丰富的数学物理背景,其解的存在性刻画了一个非线性Schrödinger方程和一个未知静电场相互作用所产生的驻波,在量子电动力学中用于描述带电粒子和电磁场的相互作用,同时在半导体理论以及等离子物理中也有应用[1].

我们研究了系统(1)非平凡解的存在性与多解性,所得结果更具有一般性.本文的主要结果如下:
定理1假设条件(V′)和如下条件:

成立,则当参数λ >0 充分大时,系统(1)至少有一个非平凡解.进一步地,如果此时f(x,u)关于变元u是奇函数,则系统(1)有无穷多对非平凡解.
注1在文献[5]中,利用Ambrosetti-Rabinowitz假设条件:
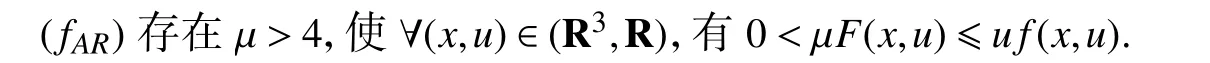
作者得到了系统(1)无穷多个高能量解的存在性.这一类型的条件目前广泛应用于利用变分方法来研究非线性方程(组)解的存在性与多解性问题的相关文献中,它的主要作用在于保证能量泛函(PS)序列的有界性.此时,定理1中对非线性项所使用的假设条件要更为一般.事实上,如果f满足条件 (f1),(f2)和(fAR),则类似于文献[12]中引理2.2的证明可知条件(f3)和(f4)成立.
1 变分框架的设立


2 主要结果的证明
引理1[7]函数φu具有如下性质:
(1)映射u→φu:Eλ→D1,2(R3)有界;
(2)映射u→ φu:Eλ→D1,2(R3)连续;
(3)如果un→u, 则φun→弱φu.
引理2[12]如果un⇀u, 则通过选取子列,存在一个序列un→u, 使当n→∞ 时,有

进一步地,如果{un}是一个(PS)c序列,则I(un-vn)→c-I(u),I′(un-vn)→0.
引理3假设条件(V′),(K), (f1)~(f4)成立,则泛函I的(PS)c序列有界.

即


并且

并且

由(13),(14)式可知

r>0 ∀u∈~EBr(0)I(u)<0e∈Eλ‖e‖Eλ>ρI(e)<0.
从而存在充分大的 ,使 , .即存在 : ,使得
显然I(0)=0.利用文献[13]中的定理2.2可知I有一个临界值 η≥α,系统(1)在Eλ中有一个非平凡解.进一步,如果f(x,u)是关于变量u的奇函数,则I(u)是关于u的偶泛函,利用文献[13]中的定理9.12可知系统(1)有无穷多对非平凡解.证毕.
