影响广西的台风极端灾害趋势风险分析

卢耀健，刘合香,2，李广桃

（1.南宁师范大学数学与统计学院，广西南宁530029；2.广西北部湾海洋灾害研究重点实验室，广西钦州535000)

1 引言

近年来，在全球变暖的气候背景下，极端天气事件频发[1-3]，给人们的生命财产安全带来极大威胁。确定极端天气事件，了解极端事件的历史趋势变化，并且预估极端灾害事件的未来演变趋势，是极端灾害风险研究的重要方面。从统计学角度看，极端事件是指发生概率高于（或低于）某一阈值的事件[4]，即末尾事件。薛联青等[5]提出了一种百分位方法来确定洞庭湖全流域的极端降水事件阈值，并研究极端降水的演变趋势，之后便有不同的学者以某一百分位值作为定义极端降水事件的标准来研究极端事件的变化规律[6-8]。侯威等[9]将去趋势波动分析法和替代数据法相结合，提出随机重排去趋势波动分析方法来确定极端事件的风险阈值，并通过数值实验验证了该方法的可靠性。杨秋珍等[10]则利用KS检验（Kolmogorov-Smirnov test）方法估计台风样本序列的理论分布，通过计算累计分布概率确定上海影响台风的风险阈值。极端阈值可分为绝对阈值和相对阈值，例如中国将每日降水量大于50 mm定义为极端降水事件是绝对阈值。本文主要讨论相对阈值，利用事件概率分布来确定风险相对阈值。

台风是广西常见的一种气象灾害。台风带来的雨水可以缓解干旱，只有台风造成的狂风暴雨、风暴潮及其次生灾害等才会给人民带来灾难，对当地居民生活造成巨大影响。确定极端台风灾害的阈值，研究极端灾害的演变趋势，了解台风极端事件的变化规律，从而采取相应的政策措施，无疑对防台减灾工作具有较大的现实意义。目前，台风研究主要从发生频率[11]、登陆强度[12-13]、路径变化[14-15]以及登陆前后的物理机制变化[16-17]这几个方面展开。对于极端台风的演变，陆逸等[18]采用了百分位法定义了极端大风并研究其变化规律。但百分位阈值的确定是基于线性假设，极端事件的变量序列一般很难满足，具有显著的非线性特征[10]，因此，在筛选极端事件时应充分考虑其概率分布的影响。广西位于华南西部，南临北部湾，靠近南海和西北太平洋台风生源地，常年遭受台风影响。本文将以影响广西的台风作为研究对象，以概率分布为依据确定风险阈值，通过研究台风影响频数、影响日期和风雨的演变趋势，探究广西的台风极端灾害风险变化。

2 资料说明

2.1 资料来源

本文所使用数据的原始资料来源于上海台风研究所整编的CMA-STI热带气旋最佳路径数据集（网址：http：//tcdata.typhoon.org.cn），后经广西气候中心整理分析得到影响广西的台风序列样本。样本包含每个台风的影响日期，以及进入影响区后最大风速和降雨量等信息，降雨量和大风数据来自91个国家气象站数据。

2.2 资料处理及说明

（1）本文中影响广西的台风是指台风中心进入112°E以东，19°N以北范围，并满足下列条件之一的台风：

①过程最大降水量≥50 mm；

②进入影响区后的最大风速≥7级；

③过程最大降水量≥30 mm，且进入影响区后的最大风速≥6级。

（2）筛选出符合上述条件的台风个例，统计出台风进入影响区后最大风速、影响广西的日期和影响过程最大降水量等。

（3）本文将符合上述影响标准的台风每次影响广西的初始日定为影响时间，由于统计资料中记录的时间为进入影响区起始日前1 d，因此需将该日期增加1 d，即为台风对广西的影响时间。

（4）本文选用了1961—2018年的台风资料进行分析，其中资料表明2004年没有台风影响广西。

3 极端事件的确定与检验方法

3.1 极端事件定义及风险阈值的确定

极端天气事件和极端气候事件统称极端事件，它是指某个异常天气或者气候变量值的发生，该值高于（或低于）该变量历史观测值区间的上限（或下限）端的某一阈值。从这一定义可以看出，极端事件即为末尾事件，在统计学意义下，其发生概率（或频率）小于或大于某一阈值时，则可被确定为极端事件。因此，若充分考虑其概率分布特征来确定极端阈值，筛选出极端事件将会更加合理。

假设X为某地历史台风影响事件的某项指标序列（例如影响该地初始时间或降水量等），F(x)则为下一台风事件的指标X不超过x的累计CDF（Cumulative Distribution Function，概率分布函数），以X≤任意实数x的概率P(X≤x)来表示，即：

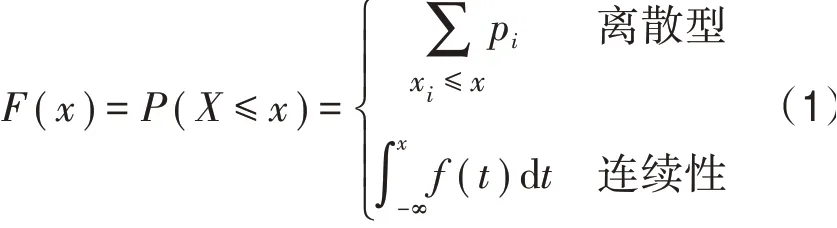
进一步地，可得超越概率分布函数：

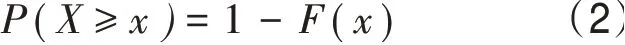
本文统一以F(x)作为台风影响指标风险衡量标准，以F(x)≤0．1作为低于下限的极端事件，以F(x)≥0．9作为高于上限的极端事件。

台风影响因子的概率分布函数F(x)的确定最为关键，在样本量较大时可采用经验累计分布函数，但是在确定准确阈值时只能预估成一个阈值区间。因此，本文将利用KS检验方法确定X的理论概率分布，对于无法确定其理论分布的变量X，将采用信息扩散模型[19]计算得到X的概率分布列，从而进一步地确定准确阈值。若影响台风事件的某一影响因子论域为：U={u1,u2,．．．,um}，通过下面的公式，可将一个单值样本xj所携带的信息分配给U中所有的点：

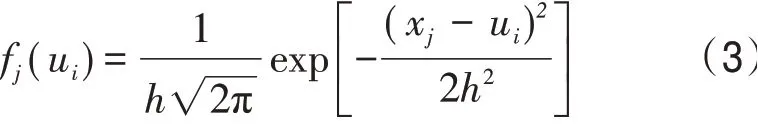
式中：h为扩散系数，可根据样本集合{xj}的最大值、最小值和样本数量确定[20]。

3.2 事件的趋势风险分析

本文将主要采用Mann-Kendall趋势性检验、突变点检验和Spearman相关性检验来分析历史台风样本的风险趋势；同时，利用重标度极差分析法（R/S）来对未来的台风影响序列时间演变趋势进行分析，并对未来的趋势风险进行大致判断。

（1）非参数M-K趋势检验[21]

定义检验统计量S：

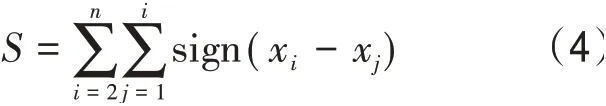
式中：

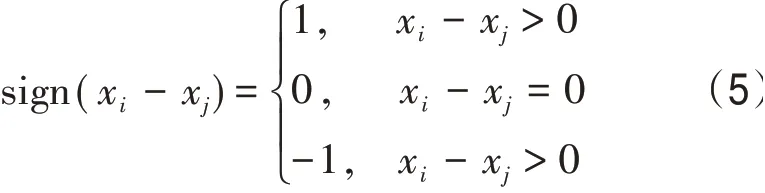
接着令：

式中：Z为正值表示增加趋势，负值表示减少趋势。

（2）R/S分析方法

R/S分析方法最早由Hurst[22]提出，是一种非线性时间序列分析的基本方法。给定一个时间序列，计算出对应时滞的极差和标准差，并求二者的比值（R/S），如果该比值随时滞呈现出幂律分布的趋势，则幂指数就是Hurst指数。计算得到H指数，可估计差分序列的自相关系数。

对于一个时间序列{X(t),t=1,2,．．．,n}，对于任意正整数τ≥1，均值序列为：

累计离差为：

极差为：

标准差为：

比值R(τ)/S(τ)=R/S，拟合幂律指数关系，即：

差分序列的自相关系数计算公式为：

式中：H为Hurst指数简写；Rt为自相关系数。根据H指数和Rt的大小可以判断时间序列为持续性还是反持续性，以及时间序列前后变化的自相关性[23-24]。当H=0．5，Rt=0，表明时间序列自相关系数为0，历史趋势与未来趋势无关；若H＞0．5，Rt＞0，表明时间序列自相关系数＞0，即时间序列变化前后呈正相关，历史趋势和未来趋势一致；若H＜0．5，Rt＜0，表明事件序列自相关系数＜0，即时间序列前后呈负相关，历史趋势与未来趋势相反。

4 结果分析

4.1 台风频数变化趋势风险分析

4.1.1 频数统计特征

1961—2018年影响广西的台风频数总计为282个。其中，年影响频数最多为9个（1974年和2013年），次多为8个（1967年、1971年、1973年和1994年）；年影响频数最少为0个（2004年），次少为1个（1997年）。将进入广西影响区时的最大风速大于32.7 m/s的台风记为强致灾台风，影响广西的强致灾台风频数总计为59个，占所有台风的20.92%。其中，年影响频数最多的为4个（1973年），次多的为3个（1963年、1978年和1992年）。影响广西的台风年平均频数为4.86个，标准差为2.02，变异系数CV1=0．42；强致灾台风年平均频数为1.01个，标准差为0.94，变异系数CV2=0．92。变异系数可以用来比较两组数据的离散程度，两组数据的变异系数均大于0.2，且强致灾台风频数的变异程度远高于影响台风频数的变异程度，表明两组数据的数据点分布不集中，分散程度较高，且强致灾台风频数的分散程度远高于台风影响频数。

4.1.2 影响频数趋势风险分析

图1给出台风年影响频数和强致灾台风年影响频数的曲线变化图。从中可以发现，1961—2018年，影响广西的台风年频数呈下降趋势，平均每年下降0.058个；强致灾台风年频数呈现出非常微弱的下降趋势，可认为在这区间范围内强致灾台风年频数并无趋势变化。我们对台风年影响频数做M-K趋势性检验，得到统计量Z=-2．565，显著性概率值P=0．01＜0．05，通过了信度0.05的显著性检验，表明影响台风年频数呈显著的下降趋势。进一步对该序列做Pettitt突变点检验，得到可能存在的突变点为第36个数据点，即1996年，该检验的显著概率P=0．009＜0．01，通过了信度0.01的显著性检验，表明在1996年后影响广西的台风年频数出现显著突变。计算两个时段的年平均频数，其中1961—1996年的年平均频数为5.56个，1997—2018年的年平均频数为3.73个，后一个时段的台风影响频数显著下降。

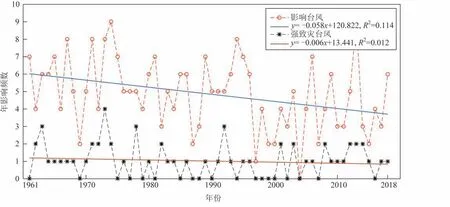
图1 影响广西的台风年频数和强致灾台风年频数变化曲线图

下面，我们进一步分析两个时段的趋势变化。1961—1996年统计量Z的绝对值基本接近0，表明该时段台风影响频数基本没有趋势变化；1997—2018年统计量Z=1．435，表明该时段台风影响年频数呈上升趋势，但显著性概率值高于0.1，上升趋势不明显。但是在对1997—2018年强致灾台风年频数进行趋势性分析时发现，统计量Z=1．78，显著性概率P=0．075＜0．1，表明在这个时间段内，影响广西的强致灾台风年频数呈现较为显著的上升趋势，这或许是因为近年来以极端强度登陆华南的台风显著增多而导致[25]。

4.1.3台风影响频数趋势演变的R/S分析

从上述分析中我们可以得知，1961—2018年影响广西的台风年频数呈显著下降趋势，1997—2018年影响广西的强致灾台风年频数呈较为显著的上升趋势，因此，将对这两个时段的年频数进行R/S分析，结果见表1。

从表1中可以看出，1961—2018年台风年频数H指数为0.593＞0.5，表明未来台风年频数的变化过程与过去具有弱的持续性，未来影响广西的台风年频数可能会继续下降；1997—2018年强致灾台风年频数H指数为0.677＞0.5，表明未来强致灾台风年频数演变趋势将与过去一致，未来影响广西的强致灾台风年频数可能会继续上升。

表1 影响广西的台风和强致灾台风演变趋势分析结果

4.2 影响广西的极早和极晚台风风险分析

4.2.1 台风影响广西的日期统计特征

1961—2018年，影响广西的台风均发生在4—12月间，最早发生在4月17日（2008年），最晚发生在12月1日（1974年），相差227 d，时间跨度较大。计算得到平均影响日期为8月14日，标准差为41.67 d，变异系数为0.18<0.2，表明影响广西的台风影响日期较为集中。影响日期的0.25分位数为7月17日，0.75分位数为9月11日，台风对广西的影响主要集中在该时间段内。

4.2.2台风影响时间分布概型及风险阈值确定

图2a给出了1961—2018年台风影响日期的频率分布直方图。从图中可以看出，影响日期的频率分布近似正态分布。估计台风影响日期序列的理论分布，得到最可能的理论分布为正态分布，数学期望为226.436（日序），标准差为41.674。利用KS检验方法对其进行检验，显著性概率值为0．546＞0．1，因此，在0.1的置信水平下，不能拒绝原假设，即该影响日期序列服从均值为226.436，标准差为41.674的正态分布。图2b为影响日期的累计经验分布图和正态分布累计分布图。图中可以看到，正态分布曲线能够很好地拟合经验分布曲线，因此利用该正态分布模型来估计台风极端早与极端晚事件阈值是合理的。

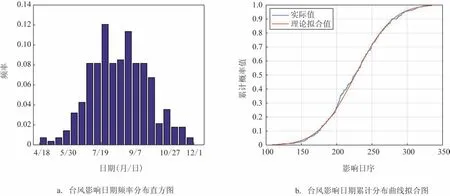
图2 广西台风影响日期频率与概率分布图

根据正态分布模型计算出相应的不同F(x)分位值的日期F-1(x)，即各个等级风险阈值，得到的结果见表2。

在表2中，我们同样利用了信息扩散方法确定F(x)的各个阈值日期。结果可以发现，二者确定的阈值日期大体一致，相差最大为3 d。由于正态分布模型能够很好地拟合影响日期的累计经验分布，因此我们依旧选取正态分布模型来确定各个分位阈值的日期。我们将早于F(x)=0．1分位阈值（6月21日）的台风影响事件定义为极端早事件，将晚于F(x)=0．9分位阈值（10月6日）的台风影响事件定义为极端晚事件；将早于F(x)=0．25（7月17日）的定义为偏早事件，晚于F(x)=0．75（9月11日）的定义为偏晚事件。其中，1961—2018年共发生了27次极早事件，分别发生在1961年、1962年、1965年、1970年、1971年、1972年、1974年、1975年、1985年、1986年、1987年、1989年、1990年、1991年、1994年、1999年、2000年、2008年、2012年、2013年、2015年和2018年；发生了28次极晚事件，分别发生在1965年、1967年、1970年、1972年、1973年、1974年、1975年、1978年、1981年、1982年、1983年、1985年、1986年、1988年、1990年、1993年、1995年、2003年、2005年、2009年、2012年、2013年和2017年。偏早事件发生了71次，偏晚事件发生了74次。我们将发生极早事件的年份称为极端早年，发生极晚事件的年份称为极端晚年，同时发现共有9 a同时发生了极早和极晚事件（见表3），使得这几年的台风影响时长比其他年份显著拉长，受台风影响造成损失的风险比其他年份大。

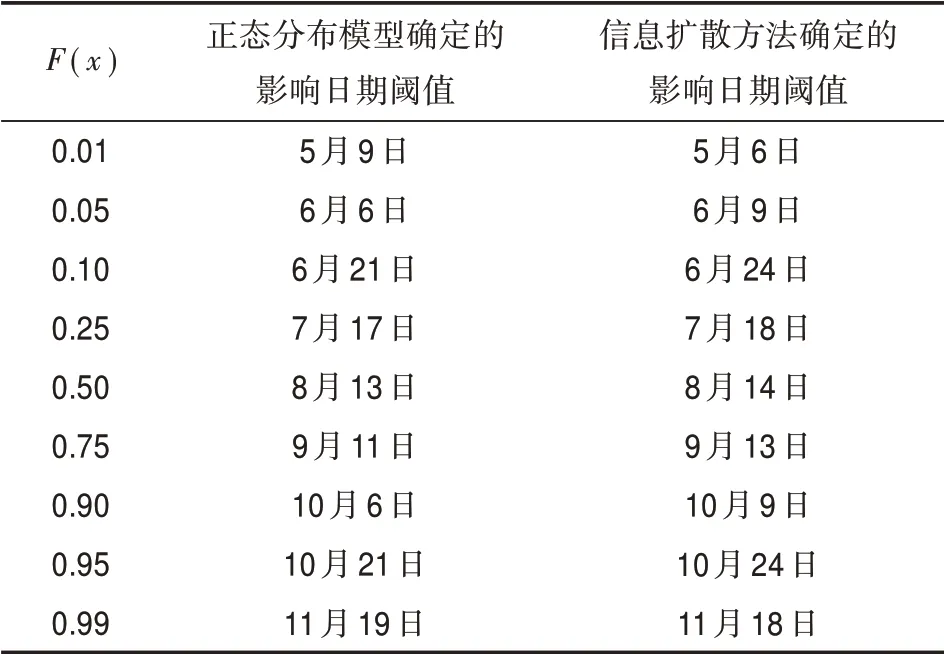
表2影响广西的台风影响日期不同风险水平阈值（1961—2018年）

4.2.3 早/晚事件趋势风险分析

根据不同年代的早/晚事件的变化趋势，研究1961—2018年极端早/晚台风对广西影响的风险变化。图3给出了不同年代的早/晚事件平均发生率的变化规律。从图中可以看出，各个年代早事件和晚事件平均发生率并不一致。在早事件中，极早事件平均发生率的年代变化规律为先上升后下降，接着上升，在1986—1995年达到最大值0.8，然后下降，在2001—2010年达到最小值0.1，之后继续上升；晚事件中，极晚事件平均发生率的年代变化规律为先上升，后下降，在1996—2005年达到最小值0.2，之后又呈上升的趋势。分析极早事件与极晚事件的年代平均发生率相关系数，发现二者的相关系数为0.699，通过了显著性水平α=0．05的显著性检验，表明二者的变化规律较为一致，当一个年代的极早事件偏多时，这个年代的极晚事件也会相应偏多，反之亦然；分析偏早事件与偏晚事件年代的年代平均发生率相关系数，二者的相关系数为0.787，同样通过α=0．05的显著性检验。因此，早事件与晚事件具有年代一致性，当一个年代的早事件偏多（少）时，那么这个年代的晚事件会有很大的可能偏多（少）。

表3 极端早和极端晚事件同时出现的年份

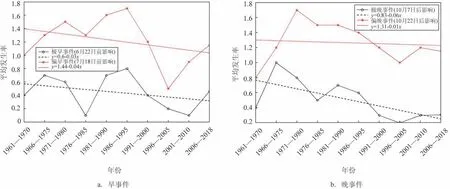
图3 台风早/晚事件不同年代平均发生率变化曲线图

4.2.4极早和极晚事件演变趋势的R/S分析

从图3的线性趋势可以发现，极早和极晚事件的平均发生率整体呈下降趋势。利用R/S方法对其未来的演变趋势进行分析，结果发现，极早事件的H指数为0.657，Rt为0.244；极晚事件的H指数为0.731，Rt为0.377。因此可以得出，事件序列在未来一段时间可能将继续维持过去的变化趋势，极早和极晚事件平均发生率在未来增长的可能性不大。

4.3 影响台风大风风险分析

4.3.1 影响台风的最大风速统计特征

在进行影响台风大风风险分析前，我们发现有两个台风个例的最大风速值为0，它们的过程累计最大雨量满足≥50 mm，符合影响广西的台风条件，但是对于最大风速而言，这两个样本属于异常值，因此我们予以剔除。

分析发现，1961—2018年影响广西的台风最大风速平均值为23.721 m/s，标准差为11.029 m/s，变异系数为0．46＞0．2，数据点较为分散。其中，最大值为72 m/s（2014年），最小值为9 m/s（1961年、1967年、1968年、1969年、1970年和1979年），最大值与最小值相差较大。选取每年影响广西台风最大风速的最大值，记为最大风速年极大值。除2004年外，广西在1961—2018年均遭受台风大风的影响，此年间的最大风速年极大值的平均值为36.596 m/s，说明广西每年很可能都会遭受一场最大风速达到36.596 m/s的台风侵扰，标准差为10.901 m/s，变异系数为0．30＞0．2，数据点也较为分散，但分散程度相对较低。

4.3.2 台风极端大风风险阈值确定

通过对影响广西的台风最大风速序列进行概率分布估计，发现拟合最接近的理论分布为伽马分布，但在利用KS方法的检验后，未能通过显著性检验。因此，正如前文提到的，对未能较好拟合理论分布的最大风速序列，我们将采用信息扩散方法对其进行概率分布估计。

最大风速序列的最小值为9 m/s，最大值为72 m/s，为了使得概率分布足够连续，将选取足够密集的点作为论域点，因此设置步长为0.1，选取论域为：U={u1,u2,．．．,u630,u631}={9,9．1,．．．,71．9,72}。

通过式（3）将所有样本点的信息扩散到论域U上，并最终计算出分布概率P(X＜x)=F(x)，这里的x将是论域U中的每一个点。图4给出了累计经验分布图和经信息扩散方法确定的累计概率分布图。从图中可以看到两条曲线非常接近，信息扩散确定的累计概率曲线能够较好地拟合累计经验分布曲线，经信息扩散方法确定的概率分布是合理的。

经信息扩散方法确定各F(x)，并得出不同阈值的最大风速F-1(x)，即台风大风的各个风险等级，结果见表4。

4.3.3影响广西的台风极端大风风险历史演变趋势

图4 影响广西的台风最大风速累计概率分布拟合图

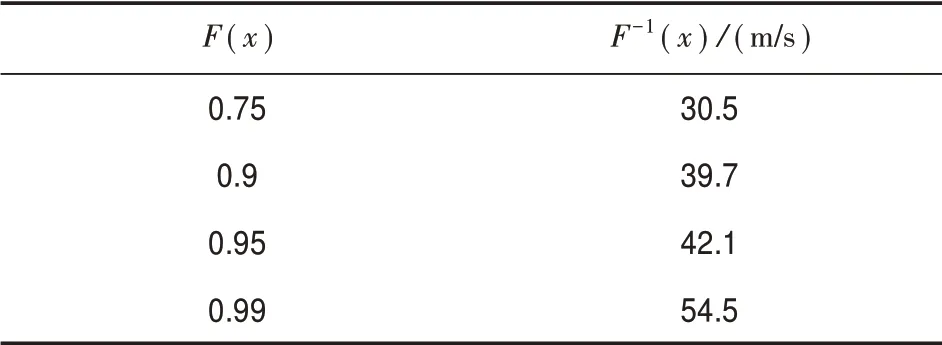
表4 影响广西台风的最大风速不同风险水平阈值

表4中，F(x)=0．9的阈值为39.7 m/s，因此我们将影响广西的最大风速≥39 m/s的台风定义为极端大风事件，当一年中出现了极端大风事件，则称该年为极端大风年。1961—2018年总共出现了33个极端大风个例，占所有台风个例的11.79%；共有26 a为极端大风年，占所有年份的44.83%，其中1963年、1973年、1982年、2003年、2012年、2013年和2014年分别出现了两个极端大风个例。

接下来，利用信息扩散方法，计算不同年代影响广西的台风最大风速≥39 m/s和≥42 m/s的超越概率，研究它们的演变趋势（见图5）。

从图5中可以看出，影响广西的台风最大风速≥39 m/s的概率随着年代的变化呈现出先减少后增加的趋势，但总体而言，1961—2018年影响广西的台风最大风速≥39 m/s的概率呈现增加的趋势，特别在2006—2018年的超越概率达到了最大值0.167；影响广西的台风最大风速≥42 m/s的概率同样随着年代的变化呈现出先减少后增加的趋势，但从总体的线性趋势看，超越概率呈增加的趋势，并且该回归曲线的斜率高于≥39 m/s的概率回归曲线，增长趋势更加明显，在2006—2018年，其超越概率同样达到了最大值0.115。因此可以得出，近年来影响广西的台风最大风速达到极端大风及以上级别的概率大大增加，极端大风风险增加。

4.3.4影响广西的台风极端大风风险未来演变趋势R/S分析

对各个年代影响广西的台风最大风速≥39 m/s的概率变化进行R/S分析，计算得到H=0．735，Rt=0．384，表明在未来影响广西的台风最大风速≥39m/s的概率将可能继续增长。

接着，对各个年代的台风最大风速≥42 m/s的概率变化进行R/S分析，计算得到H=0．917，Rt=0．785，表明在未来，影响广西的台风最大风速≥42 m/s的概率将可能继续增长。

图5 影响广西的极端大风不同年代概率变化图

4.4 影响台风大雨风险分析

4.4.1影响台风的累计过程最大降雨量统计特征

根据282个影响广西的台风累计过程最大降雨量，计算它们的统计特征。累计过程最大降雨量平均值为202.054 mm，标准差为140.082 mm，变异系数为0.69，远远大于0.2，数据点极为分散。数据序列的下四分位数为92 mm，表明有75%的台风给广西带来的累积过程最大雨量大于92 mm。带来过程降雨量最少的是7439号台风（12.6 mm），台风最大风速达到30 m/s；过程降雨量最多的是9411号台风（772.4 mm），台风最大风速仅为15 m/s。计算得到的最大风速序列与过程降雨量序列的相关系数仅为0.177，但是通过了α=0．05的显著性检验。因此，总体来说台风大风往往会带来大雨，但也存在“风声大，雨点小”的情况，台风大风和大雨的关系机制还需要进一步研究。

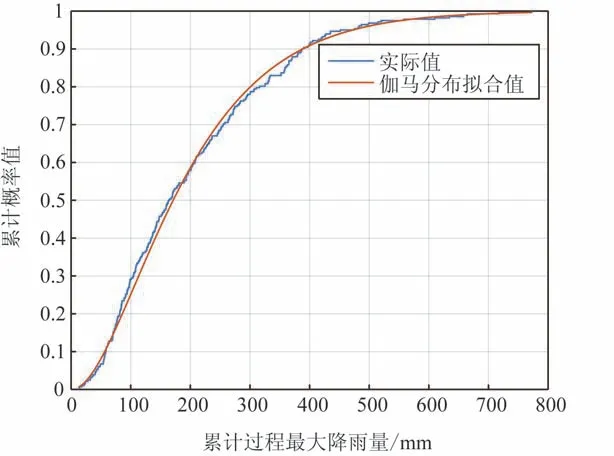
图6 影响广西的台风累计过程最大降雨量累计概率分布拟合图

4.4.2台风极端大雨风险阈值确定

对过程最大雨量序列估计得到最接近的理论分布函数为伽马分布，采用极大似然估计方法估计其参数，得到参数a=2．104，b=96．023；利用KS检验方法进行检验，结果P值为0.627，远大于0.1，那么在显著性水平α=0．1下不能拒绝原假设，过程最大雨量序列服从伽马分布，即X雨～Ga(a,b)。同样，我们绘制了经验累计分布曲线和伽马累计分布曲线（见图6），可以发现，实际值与理论拟合值非常接近，因此利用伽马分布来描述过程最大雨量并估计其风险阈值是合理的。

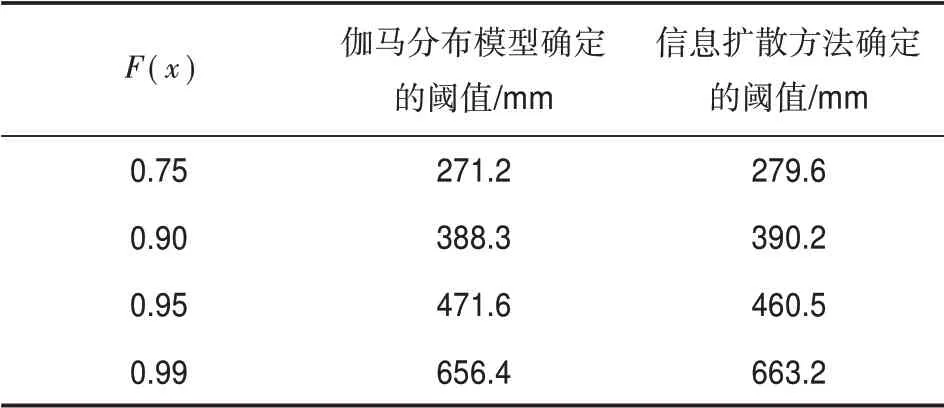
表5影响广西的过程最大降雨量不同风险水平阈值

表6 1961—2018年既是极端大风又是极端大雨的台风事件

接着，我们根据过程最大降水量服从的伽马分布模型，计算出不同阈值F(x)的过程最大降水量F-1(x)，结果见表5。从表5可以发现，伽马分布模型确定的各个风险阈值与信息扩散方法确定的相差不大，而伽马分布模型属于连续的概率分布模型，对于风险阈值确定的效果更好，因此我们选择伽马分布模型来确定各个风险阈值的降雨量。

4.4.3影响广西的台风极端大雨风险历史演变趋势

我们将台风带来过程最大降雨量≥388 mm的事件称为极端大雨事件，若该年出现了极端大雨事件，则称该年为极端大雨年。1961—2018年，共出现了28次极端大雨事件，占所有台风事件的9.93%；共有25 a为极端大雨年，占所有年份的43.10%，年份比重占比较大，其中1974年、1994年和2002年出现了两次极端大雨事件。在这28次极端大雨事件中，有5次事件既是极端大雨事件，又是极端大风事件（见表6），因此，这5次台风事件给广西带来的综合致灾风险极高，造成的损失也较为严重。例如1311号台风“尤特”导致广西12人死亡，农作物大面积受灾，直接经济损失12.82亿元。同时也可以发现，其中4次事件发生在近10 a，这也从侧面反映了近年来影响广西的台风极端灾害风险加大。

由于过程最大降雨量在F(x)=0．75的阈值为271.2 mm，因此我们将累计过程最大降雨量≥271 mm的台风事件称为普通大雨事件。利用信息扩散方法，计算不同年代的普通大雨事件和极端大雨事件的发生概率，探讨1961—2018年广西大雨的风险变化，结果见图7。

从图7可以看出，影响广西的台风过程最大降雨量≥271 mm的概率随着年代的变化整体呈上升趋势，2001—2010年间超越概率达到最大值0.408，但2006—2018年超越概率出现下降趋势；影响广西的台风过程最大降雨量≥388 mm的概率随年代的变化呈现上升的趋势，同样在2001—2010年超越概率达到了最大值0.2，之后出现下降趋势。接着对普通大雨事件和极端大雨事件的发生概率进行趋势性检验，普通大雨事件超越概率序列的统计量Z=2．326，P值为0.02；极端大雨事件超越概率序列的统计量Z=2．504，P值为0.01。二者均通过了α=0．05的显著性检验，存在显著的上升趋势，而极端大雨事件超越概率的上升趋势更大。因此，近段时间以来，影响广西的大雨事件概率呈现上升趋势，特别是极端大雨事件概率上升趋势更为明显，广西的大雨风险加大。

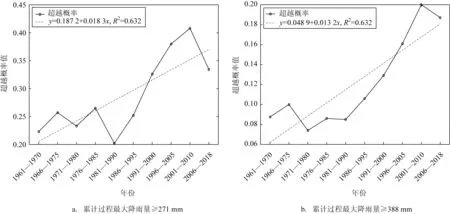
图7 影响广西的台风大雨事件年代概率变化图

4.4.4 影响广西的台风大雨风险未来演变趋势R/S分析

在了解影响广西的台风过程最大降雨量≥271 mm和≥388 mm的超越概率历史趋势后，利用R/S分析方法研究其在未来的演变趋势。通过计算得到极端大雨超越概率的H=0．992，Rt=0．997，表明在未来存在强持续性，未来发生极端大雨事件的概率将持续增长；普通大雨超越概率的H=0．970，Rt=0．918，同样在未来存在强的持续性，未来大雨事件概率将持续增长。

5 结论与讨论

探究了影响广西的台风与强致灾台风的演变趋势，以概率分布模型为基础确定了台风影响时间和风雨极端事件的风险阈值，分析极端事件的变化规律，采用重标度极差分析方法对未来台风灾害事件的发展趋势做了初步分析，得到以下结论：

（1）1961—2018年影响广西的台风频数呈下降趋势，但近年来强致灾台风频数具有较为显著的增长趋势；在R/S分析下，未来影响广西台风频数将可能继续减少，而强致灾台风频数将继续增加。

（2）影响广西台风日期服从正态分布，极早与极晚台风事件具有年代一致性，不同年代影响日期风险阈值并未发生太多变化，极早与极晚台风事件平均发生率随着年代的变化均呈现出下降趋势；在R/S分析下，未来的极早与极晚台风事件平均发生率将可能维持历史趋势。

（3）采用信息扩散方法确定台风大风风险阈值，过去58 a间极端大风的发生概率呈现先下降后增加的变化规律，总体为增长趋势，近年来极端大风的发生概率达到最大；在R/S分析下，极端大风事件的概率变化将会维持历史趋势，可能会继续增长。

（4）影响广西的台风累计过程最大雨量服从伽马分布，过去58 a影响广西的普通大雨和极端大雨事件发生概率均有显著的上升趋势；在R/S分析下，未来广西台风大雨的演变趋势将维持历史演变趋势，大雨事件发生概率可能继续增大。

针对上述分析结果，可见近年来影响广西的台风频数呈下降趋势，但是极端台风的风险与以前相比增加不少，极早和极晚事件的平均发生率下降表明台风影响日期可能会更加集中，然而极端大风和极端大雨的事件概率却在近年来显著增大。R/S分析也表明未来的防台形势更加严峻，因此需时刻关注极端台风的变化规律，制定相应防范极端台风的政策措施，达到降低风险的效果。