EC细网格产品在复杂海岛地形条件下的大风滚动订正释用
2021-06-04於敏佳刘菡王倩胡潇杰
於敏佳,刘菡,王倩,胡潇杰
(舟山市气象局,浙江舟山316000)
1 引言
舟山地处中纬度地带,是“丝绸之路经济带”和“21世纪海上丝绸之路”的交汇点,区位优势明显。习近平总书记2015年视察舟山时指出:“舟山港口优势、区位优势、资源优势独特,其开发开放不仅具有区域性的战略意义,而且具有国家层面的战略意义”。舟山港航经济发展蓬勃,宁波-舟山港连续10 a货物吞吐量全球第一,宝钢马迹山、岙山兴中和新奥舟山LNG等港口也承接着大量的矿石中转和油气储运等业务。然而,舟山灾害性天气四季频发,年平均8级以上大风日数142.7 d,其中8~9级大风日数129.2 d,10~11级大风日数12.7 d,12级以上大风日数0.8 d[1]。同时舟山群岛地形复杂,舟山沿海各海域受岛屿和山系遮蔽影响,使得各海域风力具有明显的局地性特征[2]。针对舟山各港口风力局地性特点,业务上已开展了各港口风力专业专项预报服务。经过多年的EC数值模式预报与站点实况风力对比,已得出各港口风力预报实况偏差的定性经验判断,但并未获得精确定量的订正数值。因此,应用EC细网格数值预报产品,做好舟山各港口风力预报释用,为舟山港航经济发展提供气象保障,具有十分重要的意义。
关于数值预报产品的释用,目前我国已有较多的科技人员进行了深入研究。唐跃等[3]采用双线性内插法和滑动平均误差法,进行舟山港口大风的本地化释用,并建立了各类指标和预报模型。张娟等[4]将BP(Back Propagation)人工神经网络引入到风暴潮数值预报的解释应用中,对风暴潮的数值预报结果进行订正;陈德花等[5]应用BP人工神经网络方法对MM5中尺度数值模式进行了福建沿海大风的释用;党英娜等[6]应用极差分析订正的方法对T639和MM5数值模式产品进行释用;陈豫英等[7]利用MM5模式的站点输出产品,采用多元线性和逐步回归的模式输出统计方法(Model Output Statistics,MOS)进行风的精细化释用;金龙等[8]利用模块化模糊神经网络方法进行数值预报产品释用;刘鸿升等[9]设计了最大值-阀值综合集成法,利用欧洲中期天气预报中心(European Centre for Mediumrange Weather Forecasts,ECMWF)中期数值预报,进行了偏北大风的数值预报释用;李江萍等[10]初步探讨了统计降尺度法在数值预报产品释用中的应用;钱燕珍等[11]将支持向量机(Support Vector Machine,SVM)回归方法应用于近海和登陆热带气旋的强度预报,对全球预报系统(Global Forecast System,GFS)数值预报产品进行了释用。以上方法都提高了预报准确率,取得了一定的释用效果,但对于地形的风力影响研究较少,且随着模式预报水平的不断改进,释用模型也应随之更新。本文在研究释用方法的基础上,进一步探究释用模型的滚动订正方法。
2 资料
模式资料采用EC细网格2017年1月1日—2019年6月30日每日20时(北京时,下同)再分析资料,其中2017年1月1日—12月31日为释用模式建模样本;2018年1月1日—12月31日为独立释用模式检验样本;2018年1月1日—2019年6月30日为模型回归参数滚动订正样本。
观测资料为舟山嵊泗国家基准站逐时10 m极大风向风速,该站站点观测资料经人工控制,数据完整,且具有较高的准确性和代表性。
采用双线性插值法将EC细网格10 m风再分析产品插值到观测站点上,站点信息见表1。

表1站点信息
3 释用方法
3.1 站点风速高度订正
由于风速随高度的升高而增大,各站点在对比EC细网格10 m风资料时,首先需要进行风速的高度订正。根据之前的研究[12],指数律模式能较好地反映风速随高度的变化。
指数律:

式中:u和u1分别为距地面高度z和z1处的风速;m为风速随高度的切变指数,其值的大小即表明了风速垂直切变的强度;嵊泗基准站为草地下垫面,m取0.14。
如图1所示,经高度订正后,EC再分析插值风速与实况风速误差明显改善。
3.2 考虑地形的PP法建模
在大尺度运动中,当不考虑摩擦力和地形时,空气质点的运动遵从地转风规则,这是我们进行风预报的基础。但在实际中,会有地形作用且摩擦力不为零的情况。
摩擦力方面:近地面层摩擦力来自于粗糙的地面及近地面层空气的粘性力,而空气粘性力主要由湍流活动引起,近地面层湍流与低层温度层有关,即与大气稳定度相关。由于摩擦力的存在,定量表示地面风有一定困难,难以精确估计摩擦力的大小。从实测风的读数可见,风向和风速均存在着明显的脉动现象,只能以自记曲线的10 min平均作为平均风,而以某一时段中最大平均风作为该时段的平均风[7]。挑选因子时应从大气稳定度入手,寻求表示估计偏差风的统计关系式。基于以上理论和人工经验,挑选50个与大气稳定度有关的因子。这些因子包括4个层次(地面、850 hPa、700 hPa和500 hPa)的再分析场,即温度、风、比湿、相对湿度、温度平流、水汽通量散度、涡度、垂直速度、散度、位涡和位势高度等热力动力因子。
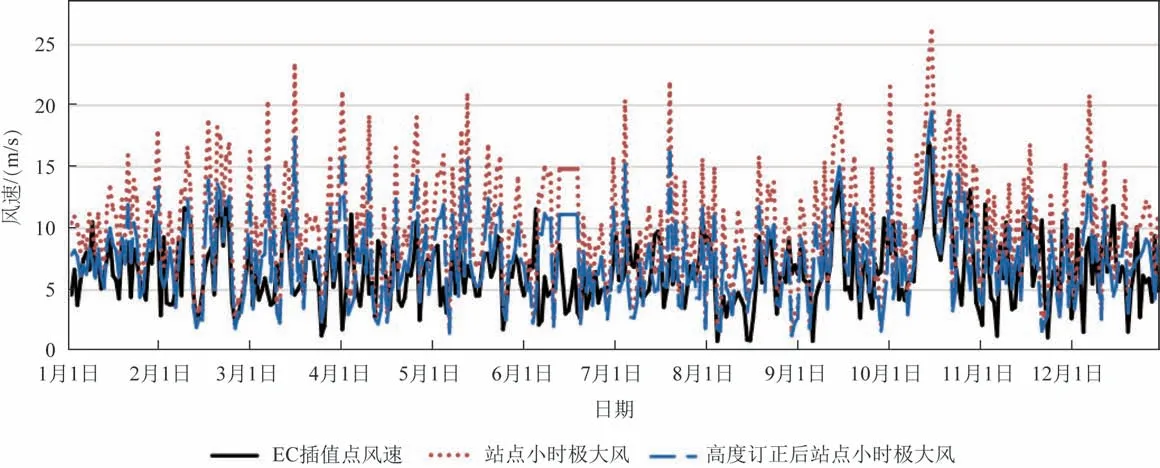
图1 2017年1月1日—12月31日每日20时EC插值点风速、站点小时极大风和高度订正后站点小时极大风对比
由于不同的物理量有不同量纲,需要先对各预报因子作标准化处理,本文采用正规化方法处理。应用多元线性回归方法对2017年整年观测和再分析标准化资料建立回归方程。经计算,方程线性关系显著性F=2.66,查F分布表F(50,314)的99%分位数为2,可见线性关系为显著。计算出单个自变量显著性t值(见表2),按0.01显著性(t 0.99(314)=2.59)T检验标准对因子进行排序筛选,保留了28个相关性较大的因子,建立PP法模型。
PP法回归方程:
YS=XSB+ε (2)
式中:YS表示站点高度订正标准化风力;XS表示700 hPa位势高度、850 hPa温度、EC插值点风力和1 000 hPa相对湿度等28个标准化预报因子;B表示待估参数;ε表示随机误差。
地形方面:风速的大小除与水平气压梯度有直接关系外,与地形也有较大关系。舟山群岛地形复杂,各观测站点多有地形影响,主要包括山体阻挡使风力减小、狭管效应和爬坡使风力增大等。地形不管以哪种形式对风力产生影响,具体表现在站点风力测量都在相同气压梯度下,不同风向的站点风速大小不同,因此,本文采用分风向的方法,具体研究地形对站点风速的影响。

图2 嵊泗站各风向多元回归预报与高度订正后风速误差箱线图
按16方位的风向进行研究,分别计算嵊泗站在各个风向条件下,PP法模型拟合与站点高度订正的风速误差。如图2所示,我们发现拟合风速误差和风向角度呈现较明显的三角函数分布特征,风速误差和风向角度两者的相关系数高达R2=0.82。对各风向风速进行拟合,均方根误差(Root Mean Squared Error,RMSE)为0.63,拟合效果较好(见图3)。
故可得风速在不同风向角度的误差公式如下:
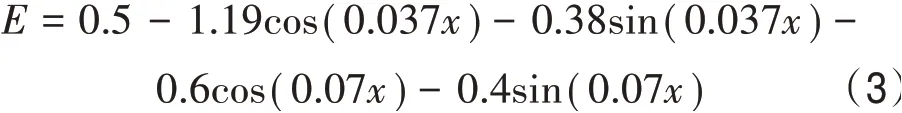
式中:E表示各风向角度下的拟合风速误差;x为风向角度。据此建立考虑地形的PP法模型。
考虑地形的pp法回归方程:
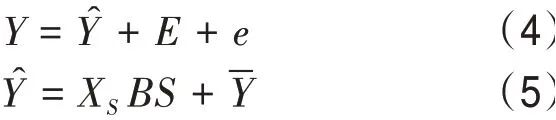
式中:Y表示站点高度订正风力;Ŷ表示多元回归预报风力;E表示各风向角度下的拟合风速偏差;e表示随机误差;XS表示700 hPa位势高度、850 hPa温度、EC插值点风力和1 000 hPa相对湿度等28个标准化预报因子;B表示待估参数;S表示Y的标准差;-Y表示Y的平均值。

图3 嵊泗站各风向风速误差拟合图
4 效果检验
4.1 订正误差评价方法
本文采用统计指标参数平均绝对误差(Mean Absolute Error,MAE)和RMSE评价模型订正前后的风速误差。具体公式如下:
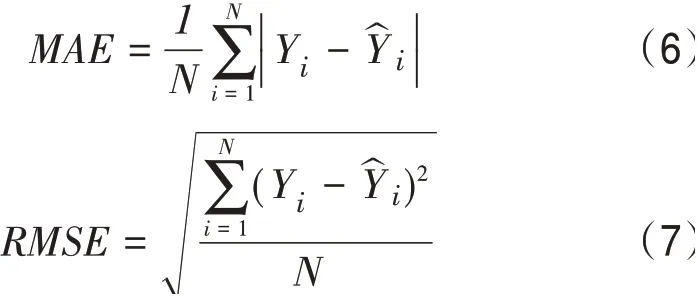
4.2 考虑地形的PP法模型检验
本文通过高度订正、PP法多元线性回归拟合和考虑地形的风力误差订正,对2017年嵊泗基准站高度订正风速和EC再分析资料进行了预报建模。每经一次订正,误差都有改进,其中高度订正后误差改进最明显,最终各项评价指标的订正结果都超过50%,具体见表2。
利用2018年全年每日20时EC再分析资料,应用所建模型进行预报,对比嵊泗站点高度订正后风速。如图4所示,模型预报误差较原始EC插值点预报误差有较大改进,计算得出MAE为2.57,RMSE为3.27,可见模型具有较好的订正能力。
5 卡尔曼滤波回归系数订正与检验
由于EC模式的预报性能和站点的气候特征都在发生变化,因此模型中的回归系数也应随时间发生变化。本文采用卡尔曼滤波法对模型回归系数进行滚动订正。卡尔曼滤波是一种数学统计方法,该方法采用量测方程和状态方程组成的线性随机系统状态空间模型来描述滤波器,并且利用状态方程的递推算法对滤波器的状态变量做出最佳估计,从而求得滤掉噪声的有用信号的最佳估计[13]。卡尔曼滤波一般用来处理滤波、预测和平滑3方面的问题。
天气预报领域中的卡尔曼滤波的基本公式如下:
量测方程:

状态方程:
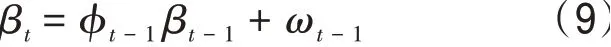

表2嵊泗站点2017年1月1日—12月31日20时高度订正前后、多元回归拟合后和风向修正后风速误差对比
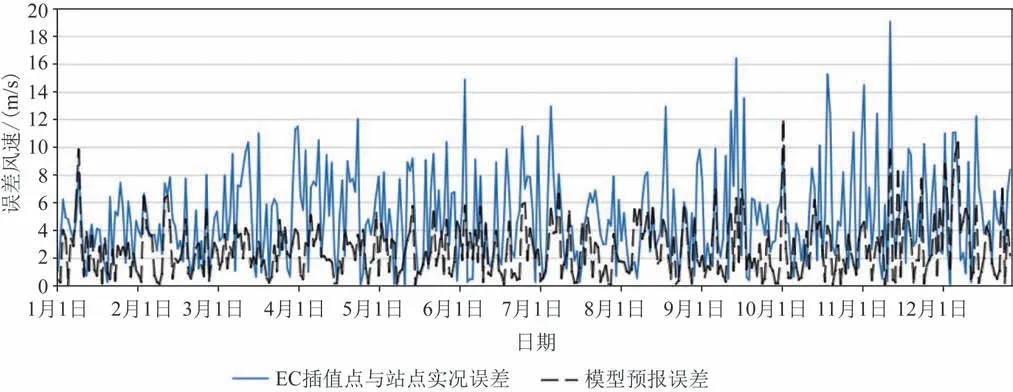
图4 2018年1月1日—12月31日每日20时原始误差与模型预报误差对比



图5 2018年1月1日—2019年6月30日每日20时卡尔曼滤波滚动订正前后风速绝对误差对比
6 结论
本文根据EC细网格资料和嵊泗站点实况资料,建立了考虑地形的PP法模型,用卡尔曼滤波法滚动更新回归参数,以MAE和RMSE作为误差订正评价指标,得出以下结论:
(1)对风速的高度订正,能有效降低EC细网格模式的预报误差,MAE和RMSE由高度订正前的4.47 m/s和5.51 m/s降至高度订正后的2.70 m/s和3.53 m/s,误差减幅分别为40%和36%。
(2)用PP法建立的站点高度订正风速和EC模式10 m风场、700 hPa位势高度和850 hPa温度等预报因子间的多元线性回归方程,方程线性关系显著性F=2.66,查F分布表,F(50,314)的99%分位数为2,具有显著的线性关系。
(3)分析各风向的拟合风速误差,发现风速误差与风向角度存在明显的正余弦函数关系,拟合后相关系数R2=0.82,RMSE=0.63,拟合效果较好。
(4)经高度订正、多元线性回归和分风向误差风速订正后,MAE和RMSE由高度订正前的4.47 m/s和5.51 m/s降至模型订正后的2.09 m/s和2.71 m/s,误差降幅达到53%和51%,订正效果明显。
(5)利用2018年全年资料进行模型订正释用能力检验。经计算,模型预报风速与站点高度订正风速的MAE为2.57 m/s,RMSE为3.27 m/s,模型具有较强的订正释用能力。
(6)利用卡尔曼滤波法,实时吸收最新EC细网格资料和站点实况风速资料,滚动订正所建模型的回归系数,计算得出MAE和RMSE由订正前的2.91 m/s和3.59 m/s滚动降至订正后的2.66 m/s和3.34 m/s,可见该方法具有滚动更新能力,且能进一步提高模型订正释用能力。
