计及荷电状态效益的含电动汽车微电网优化调度

徐 岩， 王晨光

(华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003)

0 引 言

电动汽车相较于传统燃油车由于其清洁高效的特性得到了政府和社会大力的推广和使用[1，2]。经过相关研究发现，借助V2G(vehicle to grids)技术，便可以将电动汽车视作一种具有时空特性的分布式储能设备，通过控制其充、放电行为，使电动汽车参与到电网的调度运行当中[3]，以避免大量电动汽车无序充电对电网带来的不利影响，甚至能够实现削峰填谷，提高电网运行的稳定性与经济性[4-6]。

由于微电网清洁、环保的特点与电动汽车的使用有着较好的互补性，越来越多的学者对微电网内电动汽车的调度问题进行了研究。文献[7]研究了智能微电网小区中电动汽车与家庭能量管理系统互动的调度策略，建立了双层优化模型，通过研究表明，随着用户对调度策略响应程度的提高，负荷特性的改善效果将越加明显。文献[8]根据可再生能源出力与负荷的实时数据，计算微电网的不平衡率,根据不平衡率发布合理地电价信息，以此对电动汽车充放电行为进行引导，实现微电网中电动汽车与可再生能源的协调运行。文献[9]根据微电网结构的特点，以及不同集群电动汽车对微电网所起作用的不同，将经济调度问题转化为了含有负荷级、源荷级和源网荷级的三级优化问题，以达到微电网系统经济性、高效性以及安全性的统一。文献[10]利用V2G技术来平抑短时剧烈的光伏功率波动，提出了微网环境下的集群电动汽车参与平抑光伏波动的控制框架，并建立了利用电动汽车充放电功率跟踪光伏出力的凸优化模型。然而上述文献均是对接入微电网的电动汽车进行集中式管理,没有考虑用户的独立自主性，并且调度中心需要进行大量的数据处理与计算，因此,考虑到集中式优化调度的缺点,基于博弈论的分布式优化调度方法已经开始了一定的研究。文献[11]通过博弈论思想来提升电动汽车调度代理商的收益，但并未考虑用户的利益；文献[12-14]基于主从博弈，分别以最小化电网用电成本和电动汽车用户充电成本为主体与从体制定分时电价引导用户充电；文献[15]则以电网负荷波动最小为目标建立主从博弈模型；文献[16]将满意度评价添加到用户效用函数当中，但该项系数的确定过于主观且难以设定。

通过对上述文献的研究发现，大多文献在建立调度模型时很少考虑电动汽车荷电状态(State of Charge, SOC)对用户日常使用便利性及电池损耗的影响，对用户的荷电状态仅使用剩余电量约束条件对荷电状态进行限制，可能导致在调度过程中使荷电状态或充放电功率在一段时间一直处于约束条件的边界值或频繁充放电，针对上述问题，本文提出了一种计及电动汽车荷电状态效益的微电网主从博弈优化调度模型，该模型中，作为领导者的微电网方制订电价政策引导电动汽车用户进行充放电；电动汽车用户则同时考虑荷电状态效益及充放电成本对电价政策进行响应。最后通过算例表明，所提方法在兼顾主从双方利益的同时，能够有效改善微电网负荷特性，并且避免了优化调度过程中电动汽车频繁、深度充放电的情况发生。

1 电动汽车接入时的微电网调度结构

图1为电动汽车接入时的微电网调度结构示意图。本文研究中的电动汽车为微电网内用户的工作车辆及私家车。微电网内的电动汽车用户在日前将电动汽车接入时间、电池信息等参数上报给微电网调度中心，微电网调度中心根据用户上报信息以及微电网内新能源出力、用电负荷的预测结果和上级电网的购售电价，向电动汽车用户发布充放电电价信息等待用户响应，然后根据用户响应方案对电价以及与上级电网的购售电量进行调整，以提高自身新能源发电消纳率以及用电经济性，完成对微电网内电能的统一调度。

图1 微电网优化调度结构Fig. 1 Microgrid optimized dispatch structure

2 基于主从博弈的含电动汽车微电网调度模型

在所提模型中，微电网将作为主从博弈[17]的领导者优先向电动汽车用户发布自身电价策略，电动汽车用户则作为跟随者，根据自身荷电状态以及与微电网进行电能交互的效益进行综合考虑，向微电网返回自身的充放电策略，微电网根据用户充放电方案不断调整电价策略，最终达成主从博弈的均衡解。

2.1 微电网用电成本模型

2.1.1 微电网模型目标函数

微电网进行优化调度的主要目的是通过引导电动汽车用户在各时段的充放电量，在提高自身新能源发电消纳率的同时降低自身的用电成本，其优化调度模型的目标函数如下：

cg,t-PEV,t·cm,t]

(1)

式中：Cmg表示微电网的日用电成本；PL,t、PP,t、PW,t、PEV,t分别为t时段的微电网负荷量、光伏发电出力、风力发电出力以及电动汽车充放电量；cg,t、cm,t分别为t时段上级电网交易电价以及微电网与电动汽车用户的交易电价。

2.1.2 微电网模型约束条件

(1)功率平衡约束

为了让电动汽车尽可能消纳微电网内新能源发电量，充分发挥自身储能特性，本文所提微电网结构内并未包含储能设备，微电网所缺电量及多余电量直接与上级电网进行交易。

PL,t-PP,t-PW,t+PEV,t+PG,t=0

(2)

式中：PG，t为微电网与上级电网在t时段的电能交互量。

(2)电动汽车交易电价约束

cm,min≤cm,t≤cm,max

(3)

式中：cm,max、cm,min分别为微电网与电动汽车交易电价的上下限。

(3)微电网交互功率约束

PG,min≤PG,t≤PG,max

(4)

式中：PG,max、PG,min分别为微电网与上级电网交互功率的上下限。本文将交互功率上下限设置为2 MW。

2.2 电动汽车充放电效益模型

2.2.1 电动汽车用户目标函数

电动汽车作为主从博弈的跟随者，在微电网调度中心发布电价信息后，以自身效益最大化为目标制定充放电策略并返回给微电网。在主从博弈模型中，若仅以电动汽车的充放电成本最低作为目标函数，电动汽车用户作为理性且利己的一方将不会考虑微电网的利益，将选择在电价最低时尽可能的充电，在电价最高时尽可能的放电，这种情况容易造成微电网负荷曲线形成新的高峰或使峰谷差增大，在快速充电的情况下会尤其明显。考虑到电动汽车各时段的荷电状态对用户日常使用的便利性有着重要意义，并且频繁且高深度的充放电对电池的长期使用有着不利的影响，因此本文提出了一种计及荷电状态效益的电动汽车用户目标函数，如下式所示：

(SOCn(t-1)-SOCn(t))，kn>0

(5)

式中：kn表示电动汽车用户n的荷电状态偏好系数，其值影响电动汽车保持的荷电状态水平；SOCn(t)表示电动汽车用户n在t时段的荷电状态水平；knSOCn(t)0.5表示电动汽车用户荷电状态所代表的效用；cm,t(SOCn(t-1)-SOCn(t))表示用户与微电网进行电能交易产生的效益。考虑到用户荷电状态效益函数通常为非递减且凸的[18]，因此本文选用幂函数作为荷电状态的效益函数，为了方便主从博弈均衡解的证明及求解，本文选择0.5作为效益函数的指数。

式(4)将荷电状态所带来的效益考虑到目标函数中，以此来避免电动汽车因电价的波动而频繁且深度充放电。同时当函数参数在一定区间内时，函数最大值存在于[0,1]之间，且随着kn的增大，其最大值点逐渐右移；而随着cm的增大，最大值点逐渐左移，该情况与模型需求以及用户实际应用需求相一致。分别改变kn、cm的数值，目标函数的变化趋势如图2、图3所示。

图2 kn对效用函数的影响Fig. 2 Effect of kn on the utility function

图3 cm对效用函数的影响Fig. 3 Effect of cm on the utility function

2.2.2 电动汽车用户约束条件

(1)电池荷电状态上下限约束

SOCmin≤SOCn(t)≤SOCmax

t=1,2,3…T

(6)

式中：SOCmin、SOCmax分别表示电池荷电状态的最小值和最大值。

(2)电池荷电状态期望约束

SOCn(T)≥SOCn,E

(7)

式中：SOCn,E代表用户n在调度结束时的期望荷电状态水平。

(3)电动汽车充放电功率约束

Pev,dc,max≤SOCn(t)-SOCn(t-1)≤

Pev,c,max

(8)

式中：Pev,dc,max、Pev,c,max分别表示电动汽车最大放电功率与最大充电功率。

3 模型的求解方法

3.1 主从博弈均衡解存在的证明

为了对含电动汽车的微电网进行优化调度，本文建立了以微电网为领导者，电动汽车用户为跟随者的主从博弈模型，主从博弈模型的策略集可通过式(8)表示，且当主从博弈的领导者及跟随者选择如式(9)、式(10)的策略时，该博弈可达到纳什均衡解。

Γ={N∪{MG},{Sn}n∈N,

{Un}n∈N,pm,C}

(9)

Cmg(S*,cm*)≤Cmg(S*,cm)

(10)

Un(S*,cm*)≥Un(Sn,S-n*,cm*)

∀n∈N,∀Sn∈S

(11)

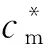
在非合作主从博弈中，当领导者及跟随者的效用函数分别为凸函数、凹函数时才会存在唯一的纳什均衡解[18]。下面对电动汽车用户效用函数为凹函数进行证明。对电动汽车用户效用函数以SOC为变量进行微分，可以得到当交易电价为cm时，使电动汽车用户得到最高效益的剩余电量为

(12)

通过式(11)可知,当kn≤2cm时，能够在[0,1]之间得到SOC的最优解。再次对Un进行二次微分得到:

(13)

式(12)中Un的二阶微分在kn≥0的条件下恒小于0，证明了式(1)在满足kn≤2cm且kn≥0的条件下在[0,1]之间恒为凹函数。

下面对微电网效用函数为凸函数进行证明。将式(11)代入式(9)，以cm为变量求式(9)的二阶微分。

(14)

当cm>0且cg>0时，式(13)中Cmg的二阶微分恒大于0，证明了式(2)恒为凹函数。通过证明可知，本文所构建的主从博弈模型微电网与电动汽车用户的效用函数，当k≤2cm、k≥0且cg>0时存在唯一的纳什均衡解。

3.2 模型求解具体流程

本文采取双层优化求解的方式对所建立的主从博弈模型进行求解，上层模型为微电网用电成本模型，以下层模型返回的电动汽车充放电量为已知量，微电网与电动汽车交易电价为变量；下层模型为电动汽车用户充放电效益模型，以电动汽车荷电状态为变量，交易电价为已知量进行求解。上下层模型采用粒子群算法[19]嵌套Yalmip工具包中的CPLEX求解器进行求解。考虑到下层模型目标函数中存在非线性项SOC(t)0.5，可在变量求解区间[0.1,1]内分段进行线性拟合，使目标函数变为分段的线性函数，使得下层模型变为混合整数规划模型，便可采用CPLEX求解器进行求解。对y=x0.5进行分段线性拟合，各段所对应的线性函数如表1所示。

表1 分段线性拟合结果Tab.1 Piecewise linear fitting results

模型求解的具体流程如图4所示。

图4 模型求解流程Fig. 4 Model solving process

4 算例分析

4.1 算例参数设置

算例中微电网基础负荷、光伏发电出力及风电出力[20]如图5所示，上级电网分时电价如表2所示，为了鼓励用户消纳自身发电，微电网向上级电网售电的价格为购电电价的0.6倍，为了尽可能保证电动汽车用户的利益，微电网与电动汽车的交易电价的上限为上级电网电价最大值，下限为0.5元。微电网内可调度电动汽车数量为200辆，调度周期为1天，可调度时间为早上8:00至晚23:00，荷电状态偏好系数kn设置为0.9，起始SOC满足0.2～0.4的均匀分布，电池容量为40 kW·h，SOC上限为1，下限为0.1，调度结束时的期望SOC最低值为0.6，充放电效率均为90%，充放电最大功率均为20 kW。

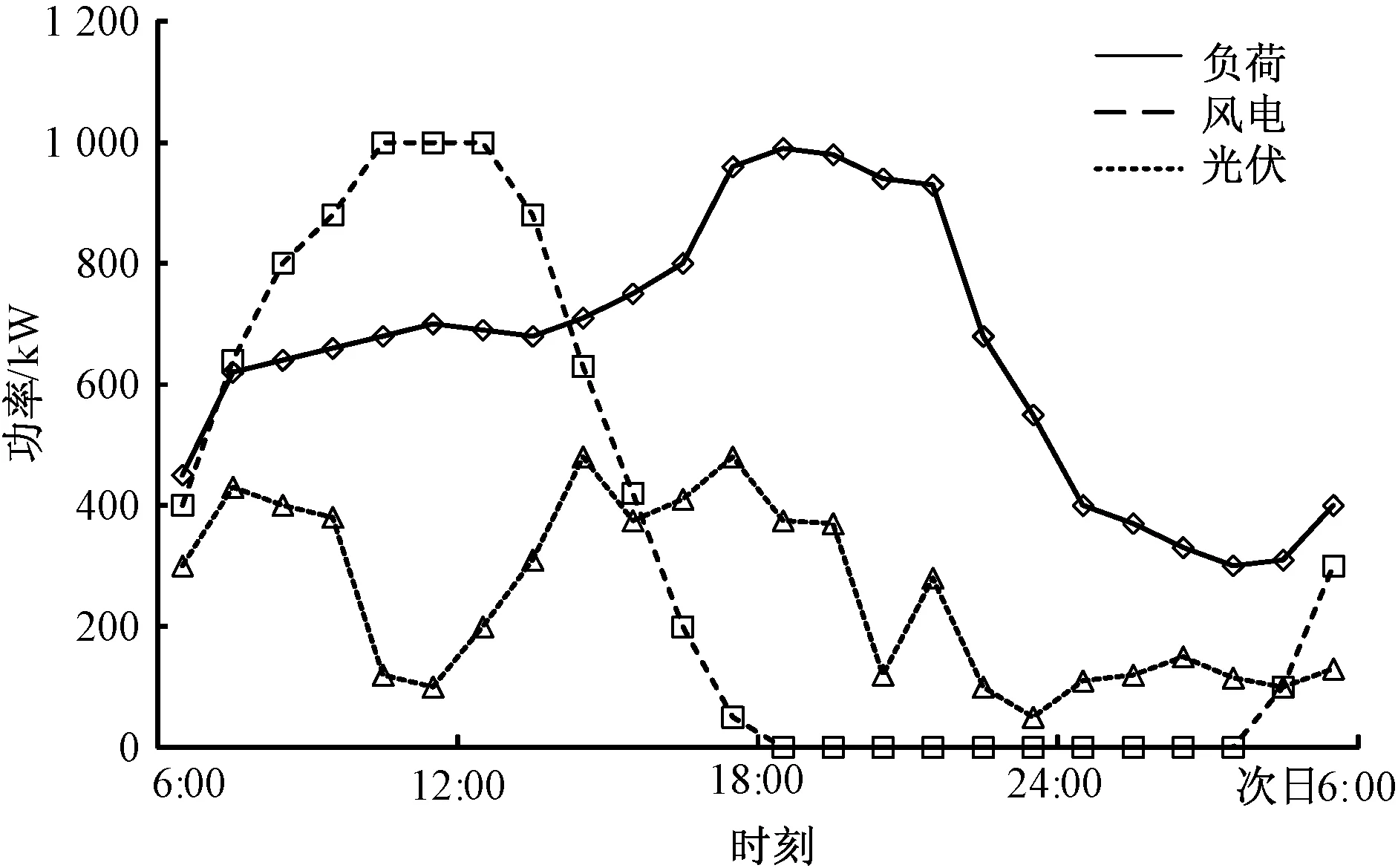
图5 微电网负荷及新能源出力曲线Fig. 5 Microgrid load and new energy output curve

表2 上级电网分时电价Tab.2 The TOU price of the upper grid

4.2 优化结果

为了验证本文所提模型的有效性，设置了三种模型进行对比仿真：方案1，微电网对接入的电动汽车进行集中调度，以微电网用电成本最低为目标进行优化调度；方案2，采用主从博弈模型，电动汽车用户仅以充放电成本最低为目标，对微电网给出的电价方案进行响应；方案3，采用主从博弈模型，电动汽车用户采用本文所提目标函数对自身充放电进行优化。优化结果如图6所示。

图6 不同方法的优化调度结果Fig. 6 Optimal scheduling results of different methods

通过对图6分析，方案1由于上级电网分时电价的影响，微电网将集中调度电动汽车在平时电价进行充电，虽然在微电网原净负荷为负时对新能源出力有着很好的消纳效果，但由于电动汽车用户在调度结束时对荷电状态有一定要求，因此产生了新的负荷峰值。方案2中电动汽车用户仅以充放电成本最低为目标制定充放电策略，将会造成自身频繁充放电，微电网负荷也因此产生了新的峰值和谷值，且增大了负荷的峰谷差。以上两种方案，在增大充放电最大功率后，其峰值及峰谷差将进一步增大。方案3由于考虑了电动汽车荷电状态的效益，用户的充放电功率会较为平缓，且在所有时段电动汽车的充放电功率均为达到所设置的最大充放电功率，同时微电网的负荷曲线也得到了明显改善。

各方案微电网负荷各项指标，用电成本及电动汽车用电成本如表3所示。

表3 不同方法优化调度结果的比较Tab.3 Comparison of different scheduling optimization results

通过对表3分析，方案2相较于其他方案，其电动汽车用户的充电成本最低，但微电网用电成本有着较大程度的增多，这是因为在主从博弈中，跟随者仅考虑自身效益而并不会考虑领导者的利益造成的。方案3由于电动汽车用户考虑了自身荷电状态的效益，不会大幅度的充放电，因此使得电动汽车用户充放电收益成本和方案2相比较高，但微电网的电价方案起到了非常好的引导作用，有效降低了微电网用电成本和负荷曲线的峰谷差。

图7为三种方案中电动汽车充放电功率随时间的变化图，通过对比可以分析得出，方案3在三种方案中有着最少的电动汽车充放电频率及最低的充放电深度，荷电状态也处于相对较高的水平。这说明方案3的调度模型在改善微电网负荷特性，降低微电网和用户用电成本的同时，还能够避免其他调度方案中出现的频繁、深度充放电的情况，能够减少对电池带来的损耗，同时荷电状态水平较高也可以使用户更好地应对意外情况而产生的不确定性的出行需求。

图7 不同方法的优充放电功率Fig. 7 EV power of different methods

图8、图9为当用户有着不同荷电状态偏好系数时，交易电价及电动汽车荷电状态水平的在调度过程中的变化情况。随着用户荷电状态偏好系数的提高，用户倾向于使荷电状态保持在较高的水平，因此微电网需要以更高的价格才能更好地对电动汽车用户的充放电行为进行引导。在不同偏好系数下仿真结果中微电网净负荷曲线并无较大差异，其中kn=1.2时相较于kn=0.9时微电网用电成本有所下降，原因是微电网对电动汽车充放电的可调度范围随kn的提高而增大，而用户用电成本则由于期望SOC的增加而有一定的提高。

图8 不同kn下的交易电价Fig. 8 Price of different kn

图9 不同kn下的荷电状态Fig. 9 SOC of different kn

当微电网中包含不同偏好系数的电动汽车用户时，微电网调度中心可以与各个用户建立点对点的交易信息，针对不同情况的用户制定不同的电价进行交易，以满足多样性的需求。

5 结 论

本文为了解决含电动汽车的微电网优化调度问题，建立了基于主从博弈的优化调度模型，同时提出了计及荷电状态效益的电动汽车用户的充放电效益函数，通过对不同优化调度方案进行对比，得到以下结论：

(1)所建立模型通过电价引导电动汽车用户进行充放电，相比于仅考虑充放电成本的电动汽车用户目标函数，所提出的计及荷电状态效益的目标函数，在优化后不仅能够有效降低微电网负荷曲线的峰谷差与主从双方的用电成本，还能防止由于电价影响而产生新的峰值以及增大峰谷差的现象。

(2)对于电动汽车用户而言，避免了电动汽车电池频繁、深度放电情况的发生，能够减少电动汽车在参与调度的过程中对电池造成的损耗，同时由于荷电状态保持在较高水平，能够满足用户不确定性的出行需求。

(3)所提方法能够最大程度的保证电动汽车用户参与微电网调度的独立自主性，微电网调度中心可以针对不同荷电状态偏好程度的用户发布不同电价，以满足用户多样性的需求。