高速冲击下多胞材料细观结构中波传播规律

2021-06-04李伟王鹏李佳罗景润李明海

装备环境工程 2021年5期

李伟，王鹏，李佳，罗景润，李明海

（中国工程物理研究院总体工程研究所，四川绵阳 621900）

泡沫材料通过自身细观胞孔结构压缩，将幅值高且脉冲短的爆炸或冲击瞬时载荷转变为幅值低且脉冲长的载荷，从而达到被防护物可承受的应力范围。因此广泛应用于航天飞行器、防护工程以及汽车撞击防护设备[1-3]，有效提高设备安全性。

为了更好地发挥泡沫材料在抗爆抗冲击设施中的缓冲作用，不仅要从宏观层面研究泡沫材料吸收冲击能量的能力，更要从细观层面研究冲击波在泡沫材料中的传播和衰减规律。与密实介质不同的是，泡沫材料由于很低的波阻抗使得传统的SHPB压杆和直接冲击等试验手段较难获取泡沫类多孔材料中的冲击波波阵面，即无法获取冲击波在泡沫材料中的传播规律[4-9]。得益于DIC数字相关技术的辅助，聚合物基泡沫材料在中速撞击下的冲击波波阵面被成功观察和识别，从而得到冲击波波速[4,8,10-13]。即使获取了聚合物基泡沫材料的波阵面，也只是其在宏观试件表面的体现，对于试件内部的冲击波波阵面状态依然未知。此外，对于金属基泡沫材料的波阵面获取依然未有试验上的报道[14-15]。鉴于金属基泡沫材料，尤其是泡沫铝材料，在防护结构上的大量应用和广泛前景，获取冲击波在材料内部的传播衰减规律，对于优化泡沫材料细观结构和宏观构型，进而提升缓冲性能具有重要意义。

基于真实泡沫细观结构的数值模拟为上述波阵面的获取提供了一条新的途径，该方法可以获取泡沫材料动力学行为的细观信息，为波阵面的获取提供了全面的观察数据。其中3D-Voronoi细观结构模拟真实闭孔或开孔泡沫结构得到广泛应用[16-23]。细观尺度上的变形局部化为多胞材料在动态载荷下的典型特征，名义应力-应变关系无法表征胞元层次上的细致变形，但由于多胞材料细观结构复杂，变形高度非均匀，大大提升了其局部变形的表征难度。近年来，廖深飞等基于多胞材料的数值计算离散位移场、连续介质力学Lagrange应变张量和最小二乘法离散局部变形梯度法，提出了局部应变场计算方法，较好地解决了多胞材料宏观尺度上的局部应变场表征问题[19,23-27]。

文中借鉴上述3D-voronoi细观结构模拟真实闭孔或开孔泡沫结构的数值模拟方法，并结合局部应变场计算方法，开展了高速冲击下冲击波在闭孔泡沫铝中的冲击波波阵面表征。采用上述方法，对有限元与局部应变法得到的冲击波波阵面进行了对比，并分析了变形模式。在此基础上，开展了基于细观泡沫结构的冲击波波阵面传播过程分析，并划分阶段，对冲击波波速的演化规律进行了分析。最后对冲击波波阵面划分阶段的合理性进行了验证。

1 基于3D-Voronoi细观泡沫结构的数值分析方法

为了更真实地描述泡沫铝材料的细观几何构型，构建了3D-Voronoi随机细观结构有限元模型。宏观泡沫的区域尺寸为80 mm×20 mm×20 mm，并在该区域内随机撒下600个按照均匀概率分布的成核点，控制成核点间的距离δ不小于给定的距离δmin，如式（1）所示。

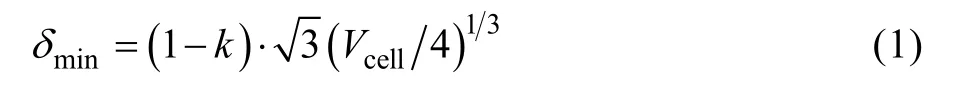
式中：k为泡沫材料中表征细观结构的不规则性；Vcell为十四面体Kelvin胞棱拓扑结构单胞的体积。

满足以上条件产生成核点后，通过Voronoi函数生成胞棱、胞面几何信息，如图1所示。采用S3R单元对胞面进行网格划分，网格特征长度为0.3 mm。假设泡沫铝具有均匀厚度，为0.2 mm。在泡沫铝模型长轴方向的上下表面添加刚性表面，下表面进行固定，上表面承受爆炸载荷作用。在泡沫铝自身内部、与刚性平面之间施加自接触，并设置摩擦系数（0.02）。整个泡沫铝模型含有600个胞元，不规则度为0.3。基材采用弹形理想塑性材料模型，密度为2.77 g/cm3，杨氏模量为69 GPa，泊松比为0.3，屈服强度为170 MPa。因此得到泡沫铝细观结构的数值仿真模型，如图2所示。采用一端冲击压缩（简称冲击端），另外一端固支（简称固支端），其中冲击端质量块为8 g，初始冲击速度为150、200、250 m/s。冲击端和固支端均采用刚性材料。

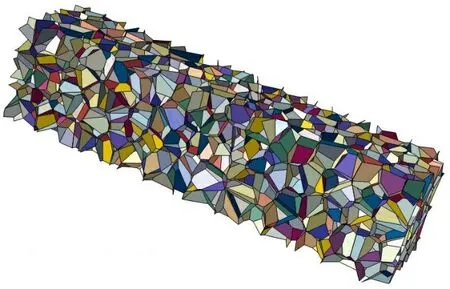
图1 泡沫铝细观结构几何图Fig.1 The diagram of aluminum foam mesoscopic structure

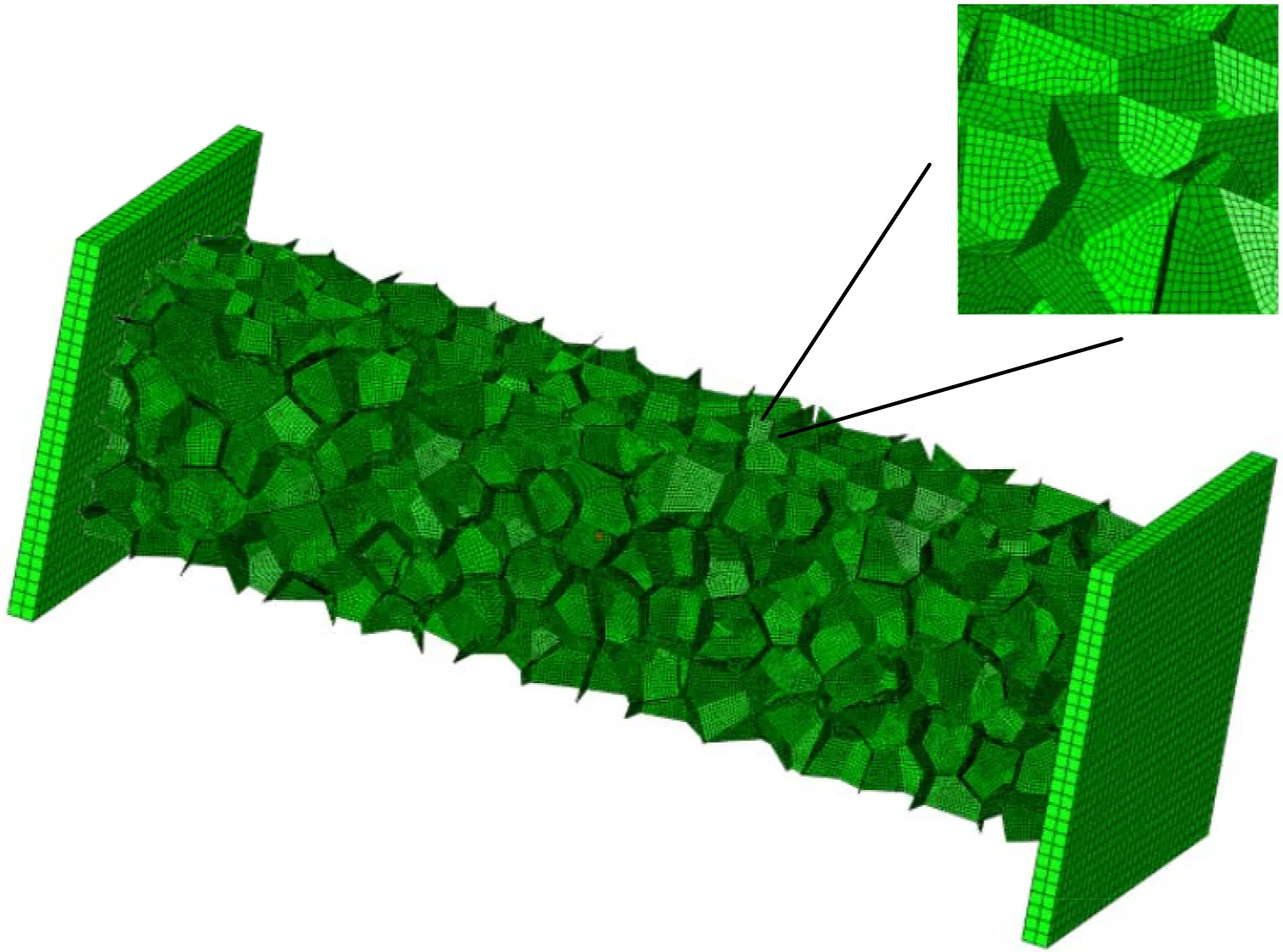
图2 泡沫铝细观结构数值仿真模型Fig.2 The numerical simulation model of aluminum foam mesoscopic structure

2 细观泡沫结构冲击波波阵面的局部应变提取法

根据连续介质力学，采用应变张量E对局部变形的表征，如式（2）所示。

式中：F为变形梯度；I为单位张量；T为张量的转置。

在多胞材料中，采用基于最小二乘法的离散局部变形梯度来描述多胞性带来的离散位移场，从而得到多胞材料的局部应变场。定义泡沫材料变形前的节点构型为Ω0，变形后的节点构型为当前构型Ω1。节点i和其相邻节点j在构型Ω0和构型Ω1中的相对位移矢量分别为Uij和uij，如式（3）和（4）所示：

式中：Xi为节点i在构型Ω0中的位置矢量；Xj为相邻节点j在构型Ω0中的位置矢量；xi为节点i在构型Ω1中的位置矢量；xj为相邻节点j在构型Ω1中的位置矢量。根据连续介质力学中局部均匀变形假定，节点i和相邻节点j之间存在唯一的变形梯度F将构型Ω0映射到构型Ω1[24]，即式（5）：

由于多胞材料细观结构的离散型和复杂性，需要对节点i及其领域一定范围内其他节点的所有构型映射变形梯度进行最小二乘法，得到节点i的最佳变形梯度Fi，如式（6）所示。

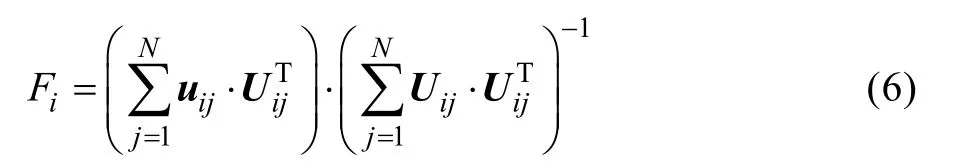
若式(6)分子中的行列式为0，则假设此时节点i处于零应变状态。其中节点i的领域半径R设定为0.5r（r为胞元平均半径）。将各节点的最佳变形梯度带入式（6），可得各节点的局部应变张量。在笛卡尔直角坐标系(1,2,3)下，可知应变张量对角线分量与局部工程应变的关系，如式（7）所示。

式中：α取值为1，2，3。

3 结果与讨论

采用上述方法，得到了泡沫铝细观结构有限元计算结果和局部应变三维图。对有限元与局部应变法得到的冲击波波阵面进行对比，并分析变形模式。在此基础上，开展了基于细观泡沫结构的冲击波波阵面传播过程分析，并划分阶段。对冲击波波速的演化规律进行分析，最后对冲击波波阵面划分阶段的合理性进行验证。

3.1 基于有限元与局部应变法的冲击波波阵面对比

在冲击端以200 m/s初速冲击条件下，首先提取泡沫铝细观结构数值仿真结果冲击方向的应力分量场、应变分量场和位移分量场，然后提取局部应变法计算得到的冲击方向局部应变分量场，对比3个时刻（0.1、0.3、0.5 ms）以上各分量场的分布状态，如图3所示。

由图3可知，由于泡沫细观结构本身不连续，泡沫铝细观结构有限元直接显示的沿冲击方向应力分量场、应变分量场和位移分量场呈现出离散状态，不能像连续介质一样呈现明显的应力、应变和位移阶段面，因此无法识别冲击波波阵面。针对以上信息场无法直接表征连续介质尺度下的局部应力和应变，通过第2节介绍的局部应变提取法，获取了局部应变分量场。从图3中可以明显观察到未扰动介质与已扰动介质的分界面，即冲击波在泡沫铝中传播的应力波波阵面，通过该阶段面的Lagrange位置信息和对应时刻，可以得到应力波波阵面随时间的变化规律。

图3 泡沫铝细观结构有限元结果与局部应变法结果Fig.3 The results comparison of finite model and local strain method for aluminum foam mesoscopic structure

3.2 基于细观泡沫结构的冲击波波阵面传播特征分析

3.2.1 传播过程及阶段划分

通过3.1的分析实例，利用泡沫铝细观结构数值模拟提供的节点位移信息，结合局部应变提取法，获取了冲击波在细观泡沫结构中的应力波波阵面传播过程，如图4所示。

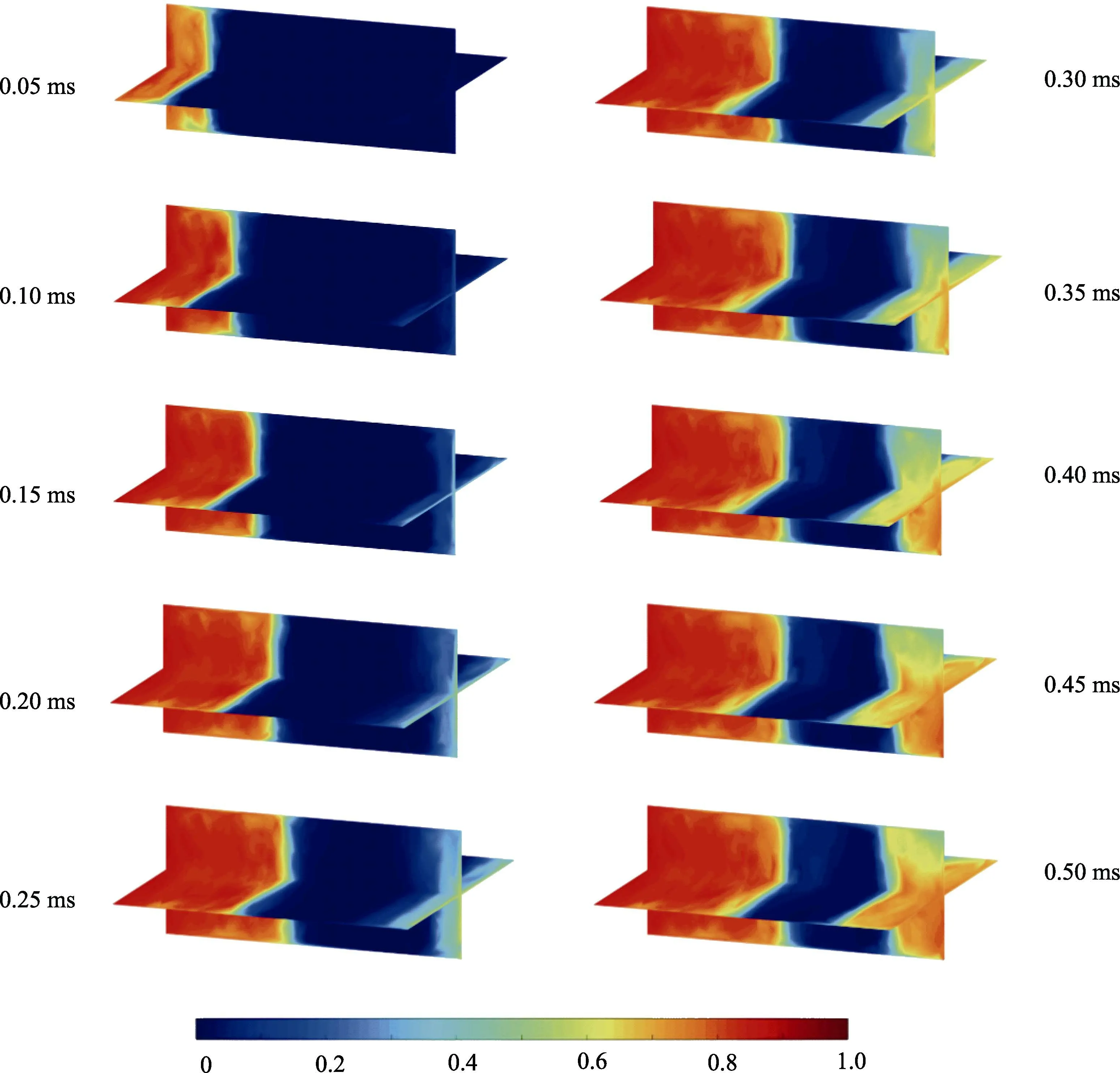
图4 冲击波在泡沫铝细观结构中的冲击波波阵面传播过程Fig.4 The shock wave front propagation process in aluminum foam mesoscopic structure

在0.05 ms，细观泡沫结构内已形成冲击波波阵面，经过该波阵面，局部应变由0跃迁至约0.7。随着冲击波继续传播，波阵面的局部应变跃迁至0.8以上，基本已压实。从冲击波波阵面在泡沫铝细观结构中的演化过程可知，尽管冲击端以初速200 m/s保持平面冲击加载，但冲击波波阵面并未完全保持平面状态。造成该现象的原因主要是泡沫材料细观胞孔结构的局部非均匀性，在宏观上可近似看作平面。在0.35 ms以后，由于冲击初始能量恒定，且泡沫材料对冲击能量持续吸收，造成冲击端产生的右行冲击波消失，即局部应变尖端面在0.35 ms以后保持Lagrange坐标位置不变。在0.15～0.2 ms，支撑端开始出现明显的应变突跃，并在随后的过程中逐渐增加，最大突跃值可达0.65，接近压实状态。对于未传播区域，处于未压缩状态，在支撑端附近的泡沫材料未压缩前，随右行冲击波的传播，未传播区域逐渐收缩，且该区域的运动速度接近于0。在支撑端附近的泡沫材料开始压缩后，且右行冲击波未消失前，该区域左、右侧同时收缩，且剩余部分近似以刚体形式向右运动。在右行冲击波消失后，该区域只有右侧收缩，右行波所过之处与未传播区域作为一体，近似以刚体形式向右运动。基于以上分析，将该过程分为3个阶段：冲击端诱发右行冲击波、支撑端诱发左行冲击波且未压缩区刚性向右运动、右行冲击波压缩区域与未压缩区域一体刚性向右运动。

3.2.2 冲击波波速演化规律

由图4分析可知，冲击波波阵面近似平面，可认为是一维冲击波传播。因此在冲击压缩垂直平面（截面）内，对应变值进行平均化处理，以表征该截面的应变。在0.05～0.5 ms内，以0.05 ms为时间间隔提取每个时刻的应变随无量纲拉氏位置的变化曲线，如图5所示。

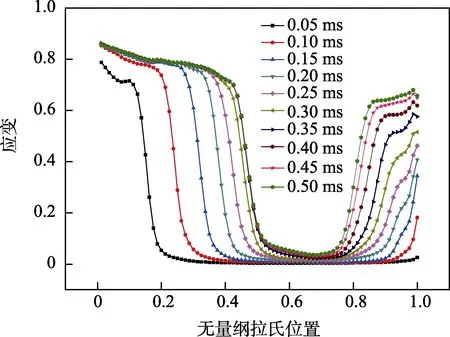
图5 冲击波在泡沫铝细观结构中的波阵面时程曲线Fig.5 The shock wave front with time in aluminum foam mesoscopic structure

由图5可知，虽然应变曲线没有呈现完全竖直状态，但斜率较大，已呈现冲击波波阵面前后应变突变的特点。通过Zheng[19]的处理方法，可以获取每个时刻理想波阵面状态下的右行和左行冲击波波阵面拉氏位置和速度，如图6所示。

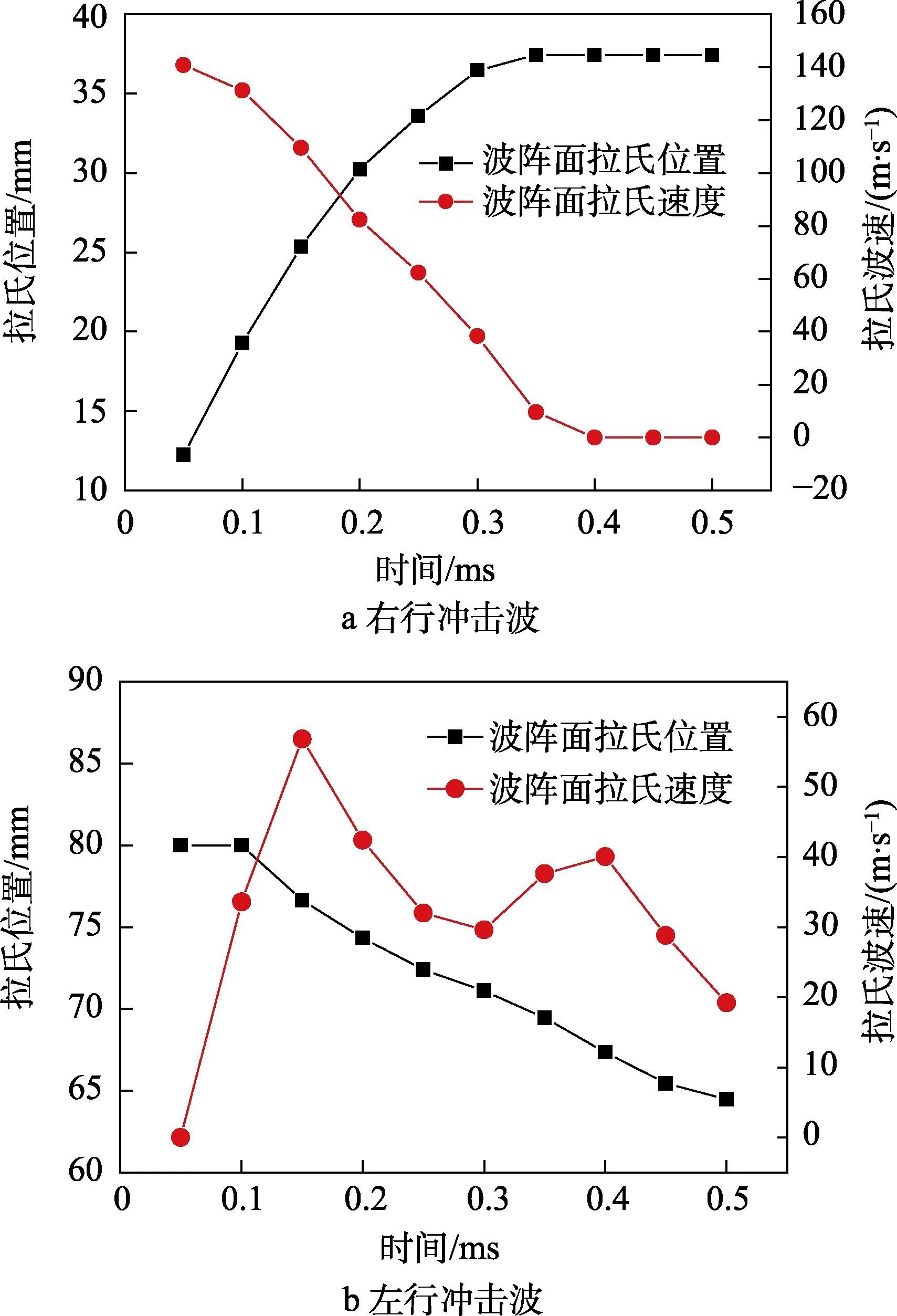
图6 冲击波在泡沫铝细观结构中的波阵面位置及速度Fig.6 The Lagrange position and velocity of right-traveling shock wave front in aluminum foam mesoscopic structure: a)right-traveling shock wave; b) left-traveling shock wave

如图6a所示，右行冲击波波阵面的拉氏位置逐渐右移，且波阵面从0.05 ms的140.8 m/s以基本恒定的加速度减小，波速曲线平滑。在0.35～0.40 ms，右行冲击波波速降低为0，且冲击波波阵面不在拉氏坐标下右移，即此时右行冲击波消失。此后，右行冲击波所过之处的泡沫材料中存在恒定的残余应变。产生以上现象的原因为：冲击端初始冲击能量恒定（冲击块为刚体，质量固定，属瞬时强加载条件），在200 m/s的高速冲击压缩过程中，冲击端附近泡沫材料由于惯性效应，产生局部压缩，并压实。压实的泡沫材料与冲击块以基本相同的速度继续冲击未压缩区域，由于细观胞壁结构的屈曲以及大量细观塑性铰的产生、传播和相互作用，泡沫材料对冲击能量进行吸收，从而造成对未压缩区域的冲击波的压缩能量降低。由应力波波阵面前后的质量、动量和能量守恒关系式（7）—（9）可知，冲击波波速也会相应下降。

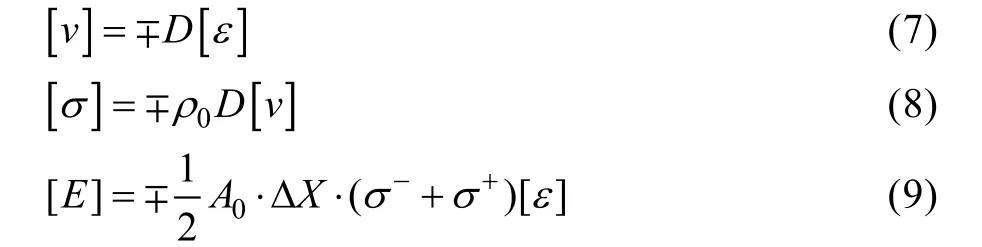
式中：[a]为波后与波前参量值之差，[a]=a--a+，其中a-和a+分别表示波后和波前参量，此处a可替换为速度v、应变ε、应力σ和内能E；D为波阵面速度；ρ0为波前泡沫材料密度；A0为泡沫材料的横截面积；ΔX为波阵面的宽度。

由于右行冲击波传播过后，泡沫材料处于压实状态，在此认为各时刻的波后状态相同，因此泡沫的吸能（内能增加）相同。设定单位体积的吸收能量为η，因此该值为恒定值，则波阵面前后的能量变化可写成式（10）：

式中：[t]为冲击波经过波阵面的宽度ΔX所用时间。将式（7）和式（8）带入式（9），并联立式（10）可得：

由图5的右行冲击波应变值可知，波前、波后的应变差[ε]基本恒定，在假设波阵面宽度不变的条件下，结合式（5）可得冲击波波阵面的加速度为恒定值。该理论分析结果与图6中的右行冲击波波阵面速度曲线在0.05～0.4 ms呈现直线下降（减加速度恒定）相吻合。如图6b所示，在0.1 ms之前，支撑端附近未产生左行冲击波。在0.20 ms之后，左行冲击波速度达到最大值，为56.8 m/s，随后出现波速下降再上升的现象。在支撑端产生左行冲击波可能是由于冲击端冲击泡沫材料初始，弹性波沿泡沫材料冲击方向传播，在支撑端发生刚性壁面反射，反射的应力波超过泡沫材料的屈服极限，因此材料开始动态压缩，未压缩区域与支撑端压缩区域产生速度差，产生内撞击，并形成左行冲击波。由于左行冲击波压缩材料被吸收能量和不断的内撞击，造成了波速下降再上升的现象。为了更好地研究冲击波在材料中的衰减现象，建立冲击波波速与波阵面的无量纲拉氏位置坐标间的关系曲线，如图7所示。

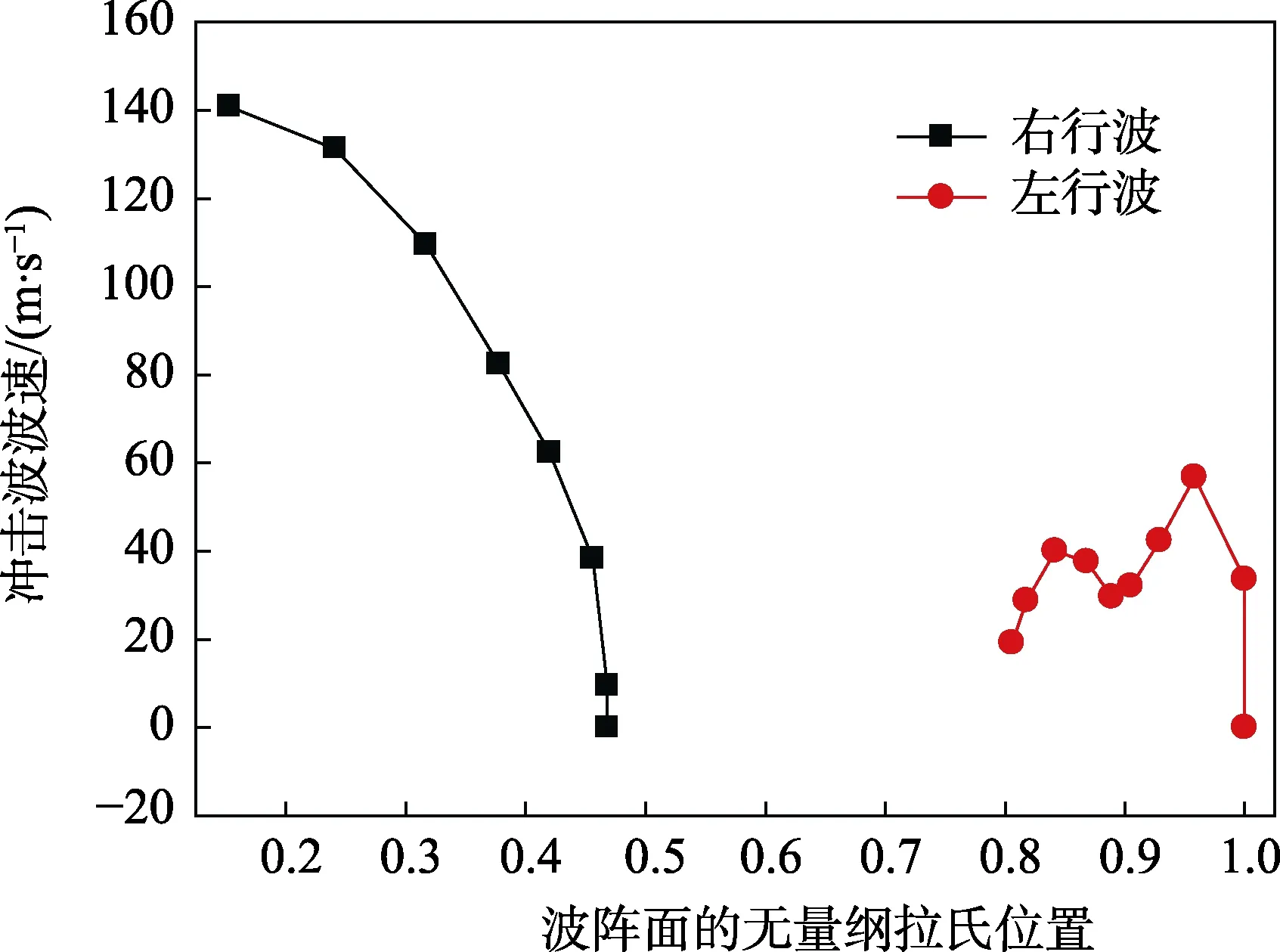
图7 冲击波波速随传播的衰减Fig.7 The attenuation of shock wave front in aluminum foam mesoscopic structure

由图7可知，右行冲击波的波速沿着拉氏位置的传播呈现出加速衰减的光滑曲线。这是由于右行波阵面减加速度为恒定值造成的，因此该曲线表现出冲击波波速为自变量，且波阵面无量纲拉氏位置为变量的二次曲线。对于左行冲击波，波速沿拉氏位置的传播依然呈现波动现象，同样该现象是由于左行冲击波压缩材料被吸收能量和不断的内撞击造成的。

3.2.3 冲击波波阵面传播阶段验证

在3.2.1节，将该过程分为3个阶段，对于第一和第二阶段，是由波阵面传播现象直接得到的，无需验证。对于第三阶段，认为右行冲击波压缩区域在右行冲击波消失后，呈现向右的刚体运动。为了验证该判断，对比了右行波阵面位置与冲击端压缩面随时间的欧拉坐标运动曲线（右行波阵面位置与冲击端压缩面之间的部分为右行冲击波压缩区域），如图8所示。

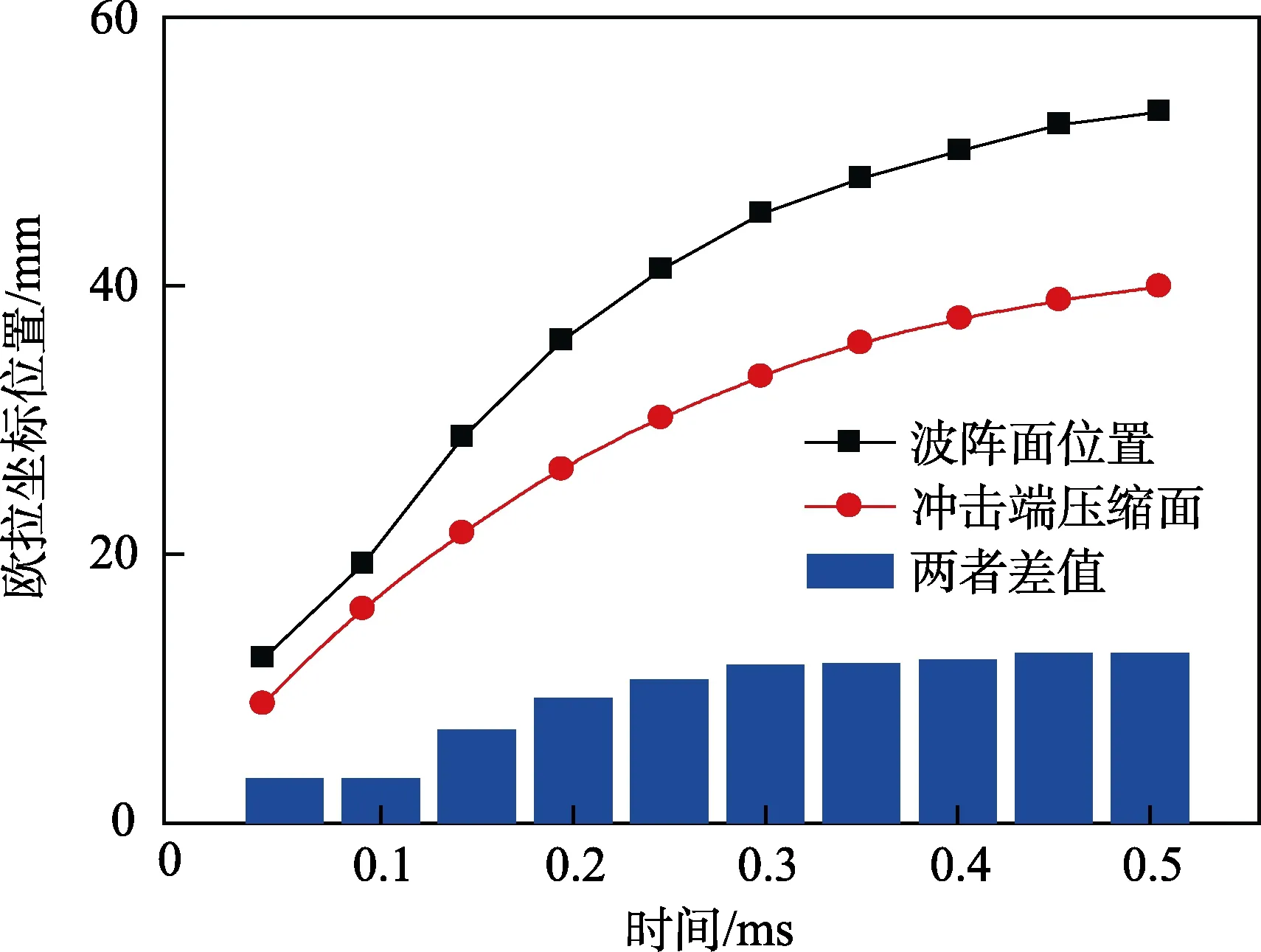
图8 冲击端压缩面与波阵面在欧拉坐标下的间距变化Fig.8 The Euler position of proximal end and shock wave front

由图8可知，在0.30 ms之前，右行冲击波压缩区域持续增大。这是由于随着右行冲击波的传播，波后的压实状态泡沫材料不断积累所致。在0.35 ms之后，右行冲击波压缩区域不再增长，保持恒定长度。说明在第三阶段，右行冲击波压缩区不再变形，而是以刚体形式联合冲击块和未压缩区域一起向右运动，与左行冲击波压缩区左端持续产生内撞击。