天然气水合物饱和度碳氧比测井的解释模型

2021-06-04李鹏举魏双宝

黑龙江科技大学学报 2021年3期

李鹏举，田甜，魏双宝

(1.东北石油大学地球科学学院，黑龙江大庆 163318； 2.东北石油大学非常规油气成藏与开发省部共建国家重点实验室培育基地，黑龙江大庆 163318)

0 引言

天然气水合物(Nature gas hydrate)俗称可燃冰，是在一定温度(一般低于300 K)、压力(一般高于0.6 MPa)、pH值等条件下由甲烷和水形成的一种形状与冰相类似的结晶物质。它可分为3种结构类型，即Ⅰ型结构(分子式为8CH4·46H2O)、Ⅱ型结构(分子式为24CH4·136H2O)和H型结构(分子式为6CH4·H2O)。据估算，天然气水合物的总资源量为目前已知煤、石油、天然气资源总量的2倍，开发潜力巨大。在天然气水合物的勘探开发过程中，地球物理测井方法是储层识别评价必不可少的一种有效方法，通过测井可以获得大量的地层信息[1-3]。

与油、水相比，天然气水合物具有较高的纵波速度，可根据此特性利用声波测井方法探测天然气水合物储层。若地层孔隙中含有固态物质天然气水合物，使用声波时差测井计算的孔隙度比真实值小，进而难以准确定量计算天然气水合物饱和度[4-7]。含天然气水合物的储层相对于邻近水层而言，通常具有更高的电阻率，油层也具有同样的性质。当地层孔隙含有天然气水合物和水或油和水这两种组合时，可利用电阻率测井方法确定天然气水合物饱和度或含油饱和度，但当地层孔隙内同时含有天然气水合物、油和水时，二者均具有较高的电阻率，电阻率测井只能计算出含水饱和度，无法分别确定天然气水合物和油的饱和度[8-10]。核磁共振测井探测的是岩石孔隙中的含氢流体，由于天然气水合物是固态，晶格中水分子的横向弛豫时间T2太短，接近岩石或沉积物骨架部分，无法被仪器探测到，因此核磁共振测井得出的天然气水合物储层的孔隙度只是含水孔隙度，其值要比真实孔隙度小很多，导致无法计算天然气水合物饱和度[11]。

上述测井方法定量确定天然气水合物饱和度时均存在一定的缺陷，为此，笔者尝试利用碳氧比测井计算天然气水合物饱和度。该方法属于中子伽马能谱测井，不受孔隙中所含物质相态(固、液、气)的影响。该方法用于探测天然气水合物储层的可行性分析如下：在地质方面，碳可作为天然气水合物的指示元素，氧可作为水的指示元素；在核物理方面，碳的非弹性散射伽马射线特征能量为4.43 MeV，氧的非弹性散射伽马射线特征能量为6.13 MeV，两者相差1.70 MeV，差值较大，这种差别为进行非弹性散射伽马能谱测井及能谱分析提供了有利条件。2000年，Collett[12]建立了碳氧比天然气水合物饱和度计算图版，明确了不同岩性条件下碳氧比值与孔隙度和天然气水合物饱和度的关系。2006年，周银行等[13]采用蒙特卡罗技术进行了天然气水合物储层碳氧比测井方法的模拟研究，计算得到了碳氧比测井响应随源距的变化关系以及不同源距时，碳氧比测井对径向深度的响应，并且得到了测井仪器长、短源距的选择范围，为定性识别天然气水合物储层奠定了基础。目前，国内外采用碳氧比测井方法探测天然气水合物储层的研究较少，测井响应规律的研究、解释模型的建立、储层参数的计算等还未形成一套完整成熟的体系。因此，笔者研究了基于能窗计数比的砂岩储层Ⅰ型结构天然气水合物饱和度碳氧比测井解释模型，为定量评价天然气水合物饱和度奠定理论基础和模拟实验依据。

1 碳氧原子数量比与孔隙度和饱和度

碳氧原子数量比测井又称脉冲中子非弹性散射伽马能谱测井，所依据的理论是非弹性散射理论。它是通过测量14 MeV的脉冲中子进入地层后，与地层中的各种元素的原子核发生非弹性散射反应而激发出的非弹性散射伽马射线等的能谱，来确定储层饱和度的一种方法[14-16]。地层孔隙度和天然气水合物饱和度的不同造成了C、O元素数量差异。若孔隙度为φ，天然气水合物饱和度为Sh、含水饱和度为SW，且Sh+SW=1。按照线性体积模型，地层中碳和氧的原子数量nc、no分别为

nc=aφSh+b(1-φ)，

(1)

no=cφSh+dφ(1-Sh)+e(1-φ)。

(2)

式(1)除以式(2)得碳氧原子数量比k为

(3)

式中：a——每立方厘米天然气水合物中碳原子的数目；

b——每立方厘米岩石骨架中碳原子的数目；

c——每立方厘米天然气水合物中氧原子的数目；

d——每立方厘米水中氧原子的数目；

e——每立方厘米岩石骨架中氧原子的数目。

已知一个碳原子的质量为1.993×10-23g，一个氧原子的质量为2.657×10-23g，一个氢原子的质量为1.674×10-24g，一个硅原子质量为4.65×10-23g，Ⅰ型结构天然气水合物的密度为0.91 g/cm3,水的密度为1.0 g/cm3，砂岩骨架SiO2的密度为2.65 g/cm3。可以算得：

(4)

(5)

1.674×10-24×2×d+2.657×10-23×d=1.0，

(6)

(7)

由式(4)～(7)可得：a=0.46×1022，c=2.63×1022，d=3.35×1022，e=5.32×1022。对于砂岩储层来说，岩石骨架中不含碳，故b=0。将a、b、c、d、e分别代入式(3)，可知砂岩储层碳氧原子数量比为

(8)

根据式(8)计算的砂岩储层碳氧原子数量比k与孔隙度φ和天然气水合物饱和度Sh的关系如图1所示。

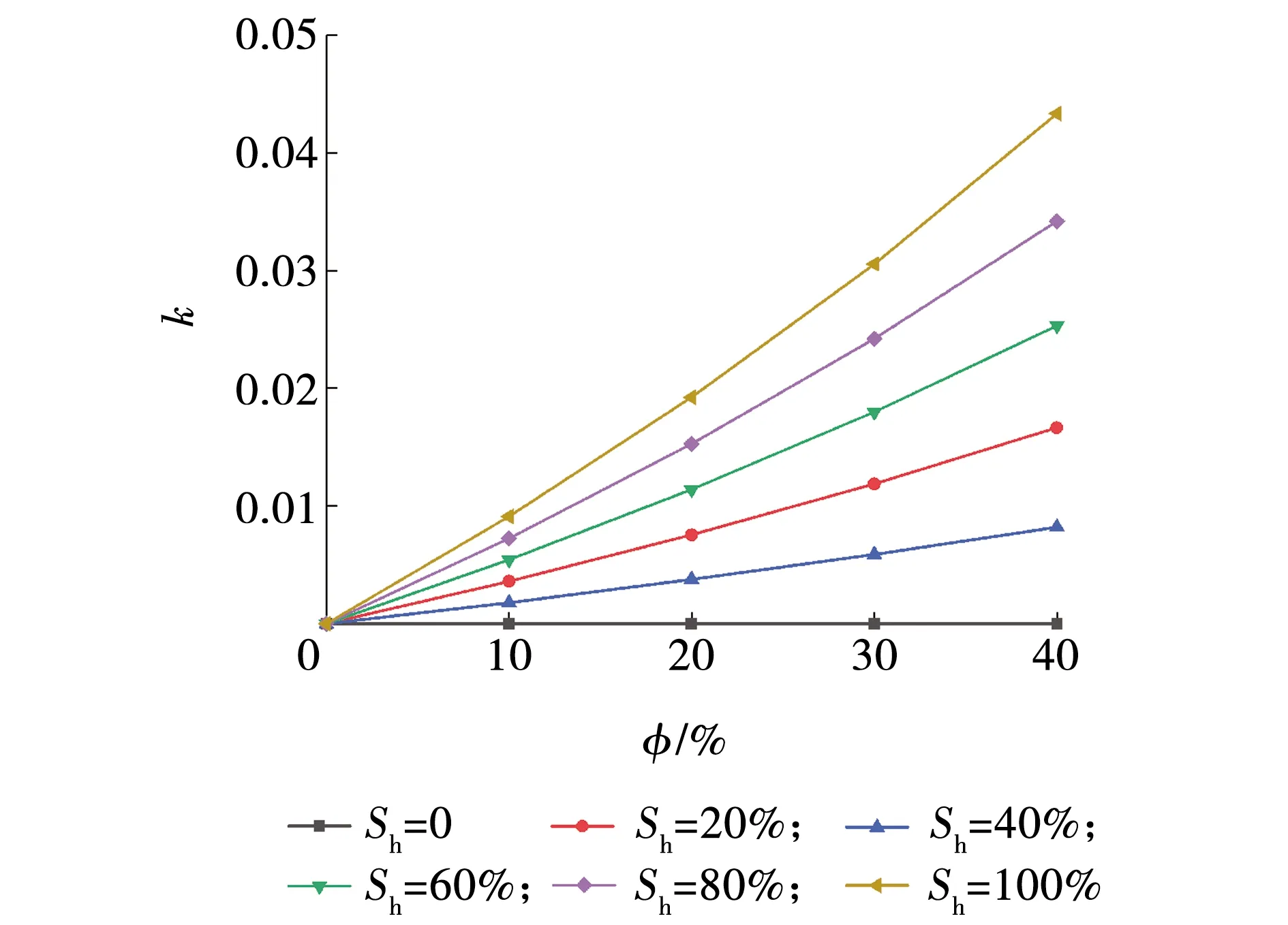
图1 k与φ和Sh的关系曲线Fig. 1 Relation curve of k with φ and Sh

从式(8)和图1可以看出，孔隙度一定时，砂岩储层碳氧原子数量比随天然气水合物饱和度的增加而增大。天然气水合物饱和度一定时，碳氧原子数量比随孔隙度的增加而增大；对于孔隙度相同的地层，天然气水合物饱和度高时灵敏度高。孔隙度和天然气水合物饱和度都高的砂岩储层有利于进行碳氧比测井，且测量精度较高。孔隙度低、天然气水合物饱和度低(含水饱和度高)的砂岩储层不利于进行碳氧比测井，测量效果不理想。

2 碳氧能窗计数比与孔隙度和饱和度

2.1 蒙特卡罗数值模拟地层模型

为确保模拟结果与实测结果的一致性，对天然气水合物储层的碳氧比测井响应研究时需建立与实际测井条件符合的物理模型。模拟使用MCNP5程序[17-18]，建立高为200 cm，半径为100 cm的圆柱状含天然气水合物纯砂岩地层模型，井眼半径10 cm，井眼流体为淡水；仪器内径8.9 cm，壁厚0.5 cm，偏心放置且良好推靠井壁；采用D-T脉冲中子源，能量为14 MeV；近、远探测器均为溴化澜(LaBr3)闪烁晶体探测器，尺寸分别为Φ76 mm×80 mm，Φ76 mm×100 mm，源距分别为27.5、52.5 cm。源与探测器、探测器与探测器之间充满理想屏蔽体。碳氧比测井蒙特卡罗数值模拟地层模型如图2所示。

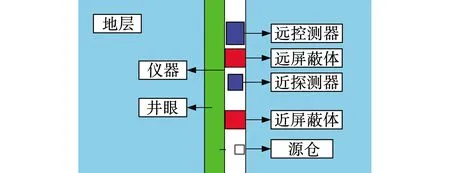
图2 碳氧比测井蒙特卡罗数值模拟地层模型 Fig. 2 Carbon oxygen ratio logging monte carlo numerical simulation formation model

基于图2地层模型，模拟得到如图3所示的非弹伽马能谱。由图3可以看出，在能量为4.43 MeV处出现C峰，在能量为6.13 MeV处出现O峰。故选取4.15～4.81 MeV作为碳能窗，4.89～6.34 MeV作为氧能窗。

图3 非弹伽马能谱Fig. 3 Non-elastic gamma ray spectrum

2.2 碳氧能窗计数比与孔隙度的关系

基于图2地层模型，模拟计算砂岩储层孔隙度对近、远探测器碳氧能窗计数比λN的影响，λN=Nc/No。由于天然气水合物储层孔隙度最大值为40%左右，并且在规律性研究中应对参数进行等距选取，因此孔隙度φ分别设置为0、10%、20%、30%、40%，天然气水合物饱和度Sh分别设置为0、20%、40%、60%、80%、100%，模拟结果如图4所示。

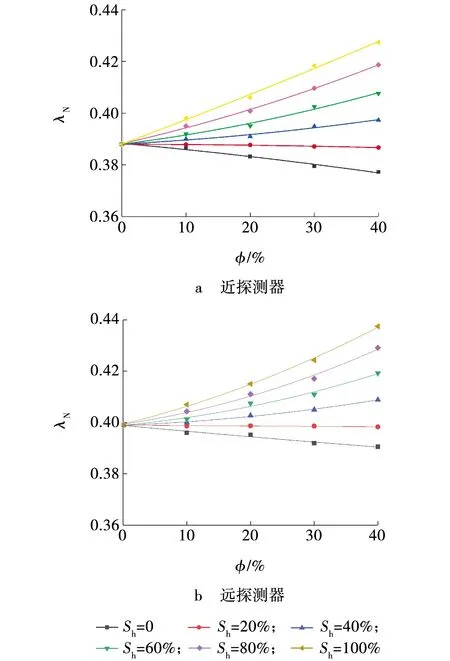
图4 碳氧能窗计数比与孔隙度的关系曲线Fig. 4 Relationship between carbon oxygen window counting ratio and porosity

从图4中可以看出，近、远探测器碳氧能窗计数比都是孔隙度的函数。当天然气水合物饱和度Sh﹤20%时，近、远探测器碳氧能窗计数比随孔隙度的增加而减小；当天然气水合物饱和度Sh>40%时，近、远探测器碳氧能窗计数比随孔隙度的增加而增大。还可以看出，孔隙度在15%～40%范围内时，地层从孔隙全部为水的砂岩变化到孔隙全部为天然气水合物砂岩的近、远探测器碳氧能窗计数比有明显的变化。这说明，碳氧比测井仪器只有在孔隙度比较大的砂岩储层中对天然气水合物饱和度的变化是灵敏的，而在低孔隙度砂岩储层中，测量精度较低。

2.3 碳氧能窗计数比与饱和度的关系

基于图2地层模型，模拟研究砂岩储层，天然气水合物饱和度对近、远探测器碳氧能窗计数比的影响。其中，孔隙度φ分别为0、10%、20%、30%、40%，天然气水合物饱和度Sh分别为0、20%、40%、60%、80%、100%，模拟结果如图5所示。

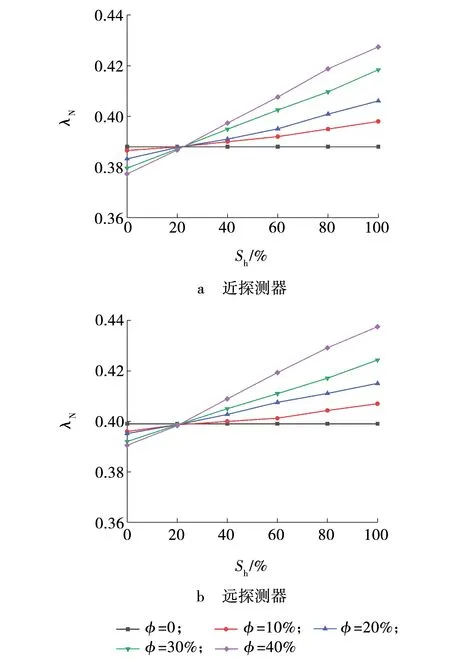
图5 λN与Sh的关系曲线Fig. 5 Curve of relation between λN and Sh

从图5可以看出，砂岩储层不含孔隙时，近、远探测器碳氧能窗计数比为定值，天然气水合物饱和度的变化对其未造成任何影响。这是因为孔隙度为0时，碳元素和氧元素的含量保持不变，所以二者的比值也是固定的。当砂岩储层含有孔隙且孔隙度一定时，近、远探测器碳氧能窗计数比随天然气水合物饱和度的增加而增大。当天然气水合物饱和度在0～20%范围内变化时，近、远探测器碳氧能窗计数比随孔隙度的增大而减小，且孔隙度为40%与孔隙度为0时的碳氧能窗计数比相对差值较小;当天然气水合物饱和度在20%～100%范围内变化时，近、远探测器碳氧能窗计数比随孔隙度的增大而增大，且孔隙度为40%与孔隙度为0时的碳氧能窗计数比相对差值较大。这说明碳氧比测井对天然气水合物饱和度Sh>20%的砂岩储层具有足够的区分水和天然气水合物的能力。

3 测井解释模型的建立

3.1 测井解释模型的理论推导

采用能窗法求取碳氧比值的优点在于碳能窗计数率和氧能窗计数率及其比值可以直接测量和计算，这为定量确定天然气水合物饱和度提供了便利。碳能窗计数率包括碳元素在碳能窗的计数率和氧元素在碳能窗的计数率，即

Nc=Ncc+Nco，

(9)

式中：Nc——碳能窗的计数率；

Ncc——碳元素在碳能窗的计数率，即碳元素的净计数率；

Nco——氧元素在碳能窗的计数率。

进一步研究碳氧能窗计数比λN、孔隙度φ、天然气水合物饱和度Sh三者的关系发现，图4中碳氧能窗计数比λN在数学上可以表示为

(10)

式中：No——氧能窗的计数率；

α——与散射截面和计数效率有关的系数；

ε——碳能窗对氧能窗的康峰比。

由于地层密度对伽马射线的输运存在影响，氧元素的非弹性散射伽马射线对碳能窗有贡献，故

ε=-βφ+γ，

(11)

式中，β、γ——常数。

将式(8)、(11)分别代入式(10)中，可得碳氧能窗计数比λN为

(12)

式(12)即为基于能窗计数比的砂岩储层Ⅰ型结构天然气水合物饱和度碳氧比测井解释模型，其中α、β、γ是模型中的待求参数。

3.2 测井解释模型的参数确定

从式(12)可以看出，α、β、γ是模型中的未知参数，以下为其确定过程：根据图4中离散数据点，Sh=0、φ=0时对应的碳氧能窗计数比值即为γ；将Sh=0，φ=10%、20%、30%、40%及其对应的碳氧能窗计数比值分别代入式(12)中，可求得β；将Sh=20%、40%、60%、80%、100%及其对应的孔隙度φ、碳氧能窗计数比值分别代入到式(12)中，可求得α。式(12)中参数α、β、γ见表1。

表1 测井解释模型中各项参数

由表1可知，近探测器测井解释模型为

0.03φ+0.39。

(13)

远探测器测井解释模型为

0.02φ+0.40。

(14)

3.3 测井解释模型的简化

基于能窗计数比建立的砂岩储层Ⅰ型结构天然气水合物饱和度碳氧比测井解释模型中含α、β、γ3个参数，每个参数的确定均存在一定误差。由于误差具有传递性，根据该解释模型计算得到的天然气水合物饱和度的误差就会增大。为提高天然气水合物饱和度计算的准确性，可对上述解释模型作如下简化：为求取目的层的天然气水合物饱和度，首先需找到孔隙度与目的层相等或相近的完全含水砂岩储层作为标准层，然后计算这两种储层碳氧能窗计数比的差值，进而确定目的层的天然气水合物饱和度。具体计算过程如下：

由式(12)可知，在孔隙度φ一定的条件下，目的层和标准层的碳氧能窗计数比的差值为

ΔλN=λN-βφ+γ。

(15)

将式(12)代入式(15)中，得

(16)

根据式(16)，在孔隙度φ已知的条件下可以求出天然气水合物饱和度Sh：

(17)

其中，近探测器处，α=1.21；远探测器处，α=1.17。

与式(12)相比，式(16)或式(17)中参数仅含α，参数的减少意味着天然气水合物饱和度Sh的计算误差减小，准确性增大。但简化后的解释模型存在一定的问题，在实际测井解释过程中，若研究地区地质条件稳定，岩性、物性变化不大，则与目的层孔隙度相等或相近的标准层易于选取；反之，标准层较难选取。因此，有时目的层与标准层的碳氧能窗计数比差值的求取会存在一定困难。

与声波测井和电阻率测井的天然气水合物定量计算方法相比，碳氧比测井解释模型具备以下优点：在含天然气水合物地层中，使用声波测井计算的孔隙度比真实值小，进而难以准确定量计算天然气水合物饱和度，而该模型不受物质相态影响，水合物计算准确性更高；在同时含有天然气水合物、油和水的地层中，电阻率测井只能计算出含水饱和度，无法分别确定天然气水合物和油的饱和度，而该模型不受地层内物质复杂程度影响，可以准确计算天然气水合物饱和度。