风氢互补的长期储能微电网容量优化配置模型
2021-06-04朱显辉
朱显辉,胡 旭,师 楠
(1.黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022; 2.黑龙江科技大学 工程训练与基础实验中心, 哈尔滨 150022)
0 引 言
全球性的资源枯竭和环境污染问题,是国际社会面临的严峻挑战之一,发展绿色可再生能源刻不容缓[1]。风能绿色、高效,但其出力的不确定性会严重影响微网的稳定运行,解决该问题的有效方法是配置风电储能单元,以消纳多余风能。
学者对风电微网储能单元的合理配置进行了较为深入的研究。姜书鹏等[2]建立了能量型储能在微网中的容量配置模型,讨论了影响容量配置的敏感性因素。刘颖明等[3]基于蚁狮算法对风电集群功率备用、储能功率和容量进行最优配置。S.Ma等[4]提出了综合考虑系统成本和储能安全性的容量配置优化方案,优化了微网的运行控制策略。微电网容量优化配置属于多目标非线性问题,难以求解全局最优。马榕谷等[5]基于改进遗传算法,对非并网风氢互补系统进行容量多目标优化。刘骄扬等[6]提出了一种双层优化方案,底层以微电网日运行成本最小为目标,上层以微网和配电网总成本最小为目标,运用NSGA-Ⅱ算法配置了微电网容量。以上研究主要采用多目标遗传算法进行模型求解,但多目标遗传算法较为复杂;而粒子群算法因鲁棒性好、速度快,在解决非线性问题时更加高效的优点得到了一定应用。张悦等[7]充分考虑影响储能设备寿命的因素,利用雨流计数法计算储能寿命,采用粒子群双层优化算法对微电网进行了储能容量优化。潘华等[8]以储能系统寿命周期成本最优为目标,考虑电网运行和蓄电池的约束,建立独立微电网储能系统的优化配置模型。
上述研究大多以系统经济性为优化目标,未考虑系统的运行可靠性,配置结果无法满足平抑功率波动的实际需求。为解决上述问题,笔者从综合考虑微网经济性和可靠性的角度出发,通过建立改进的BP神经网络模型预测风电功率,提出多目标容量配置优化方案,并规划微电网运行控制策略,基于预测功率和实际负荷曲线,采用多目标粒子群优化算法,给出微网各单元容量配置,以期为微电网容量配置优化研究提供借鉴。
1 风电输出功率预测
当前制氢储能微网系统的容量优化配置研究中所涉及的风功率数值均采用简单的理论计算获得,与实际风功率可能存在一定偏差,限制了所给容量配置结果的实用性。为此,采用粒子群优化BP神经网络模型预测风功率,基于风功率预测结果研究制氢储能的容量优化问题。
误差反向传播(BP)神经网络是一种典型的优化求解算法,但是其收敛速度慢、且求解过程受网络结构、初始权值和阈值的影响,无法保证得到全局最优[9]。为此,采用粒子群(PSO)算法优化BP神经网络模型,以提高风电功率预测结果的可信性。通过气象因子寻找相似日,将相似日气象数据与风功率数据作为训练集,确定网络结构;采用粒子群算法优化权值和阈值,进行BP神经网络的训练,运用测试集验证网络的可靠性,测试集预测误差如图1所示。
图1 预测误差Fig. 1 Forecast error
2 风储联合发电系统结构与数学模型
2.1 系统结构
风储联合发电系统主要由风力发电机组、电解槽、储氢罐、燃料电池、控制单元、AC/DC变换器以及DC/DC变换器等组成,其结构如图2所示。
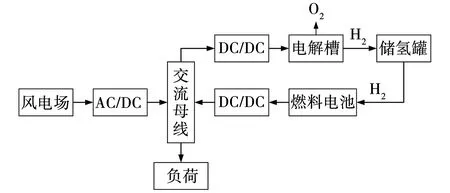
图2 微电网模型Fig. 2 Microgrid model
2.2 储能系统数学模型
储能系统为电解槽、储氢罐和燃料电池组成的氢储能系统。作为系统储能单元,当风力发电功率充足时,电解槽利用多余电能电解水制得氢气,用储氢罐进行储存。当风功率不足时,燃料电池利用存储的氢气进行辅助放电,以满足负荷需要。
以碱性电解槽为例,该电解槽通过将水电解为氢气和氧气实现能量的转换与存储,输出功率可表示为
Pe=ηePwe,
式中:Pwe——电解槽的输入功率;
ηe——电解槽的工作效率,文中取60%[10]。
燃料电池是将燃料内部的化学能转化为电能的装置,以较为典型的碱性燃料电池为例,其输出功率为
Pr=ηrPhr,
式中:ηr——燃料电池产电效率,文中取50%[10];
Phr——储氢罐向燃料电池提供氢气的功率。
储氢罐用来储存电解槽电解水产生的氢气,同时为燃料电池提供燃料,储氢罐储存的氢气能量为
式中:Δt——时间间隔;
Q(t-Δt)——上一时刻储氢量;
ηhy——储氢罐的充放效率。
3 微电网优化配置模型
3.1 目标函数
为实现微电网稳定运行,在综合考虑系统经济性和可靠性问题时确立目标函数。
3.1.1 经济性
主要以风储联合系统的运行成本和弃风造成的经济损失作为经济性目标函数。
系统总安装成本主要包括风力发电机、电解槽、储氢罐和燃料电池的安装,可表示为
Wt=Wg+We+Wh+Wf,
式中:Wg——风力发电机组成本;
We——电解槽成本;
Wh——储氢罐成本;
Wf——燃料电池成本。
风储联合发电系统在运行过程中需要对每个单元进行维护,产生运行维护成本为
式中:Ki——各单元的维护成本系数;
Pi(t)——各单元在t时刻的输出功率;
Δt——采样时间。
由于风电出力的不确定性,会出现风电出力与负荷需求不匹配的情况。当风力过剩时,储能系统不能将未利用风能完全存储,会产生不同程度弃风。
式中:K——弃风每千瓦时的惩罚因子;
QA(t)——t时刻的弃风量。
3.1.2 可靠性
系统的可靠性主要与负荷缺电率有关,缺电率指的是系统不能满足负荷功率需求的比例[11]。缺电的原因主要有两种,一种是储氢容量不足,即使氢气消耗到最低值也无法满足用户负荷,另一种是由于燃料电池功率最大值的约束,即使输出功率最大也无法满足用户负荷。其表达式为
式中:PL(t)——t时刻的功率缺额;
Pad(t)——t时刻的负荷需求。
综上,总体的目标函数表示为
(1)
3.2 约束条件
为使微电网得到合理的容量配置,要在微网供需平衡的基础上,考虑系统各单元的容量约束以及充放电功率限制。
3.2.1 功率平衡约束
为保证微电网的安全稳定运行,要保持系统的功率平衡
(2)
式中,Pd——负荷功率。
3.2.2 充放电深度约束
由于储氢罐不能快速释放所有能量,因此在储氢和释放氢气过程中有一定的限制,设置等效荷电状态作为约束范围[10]:
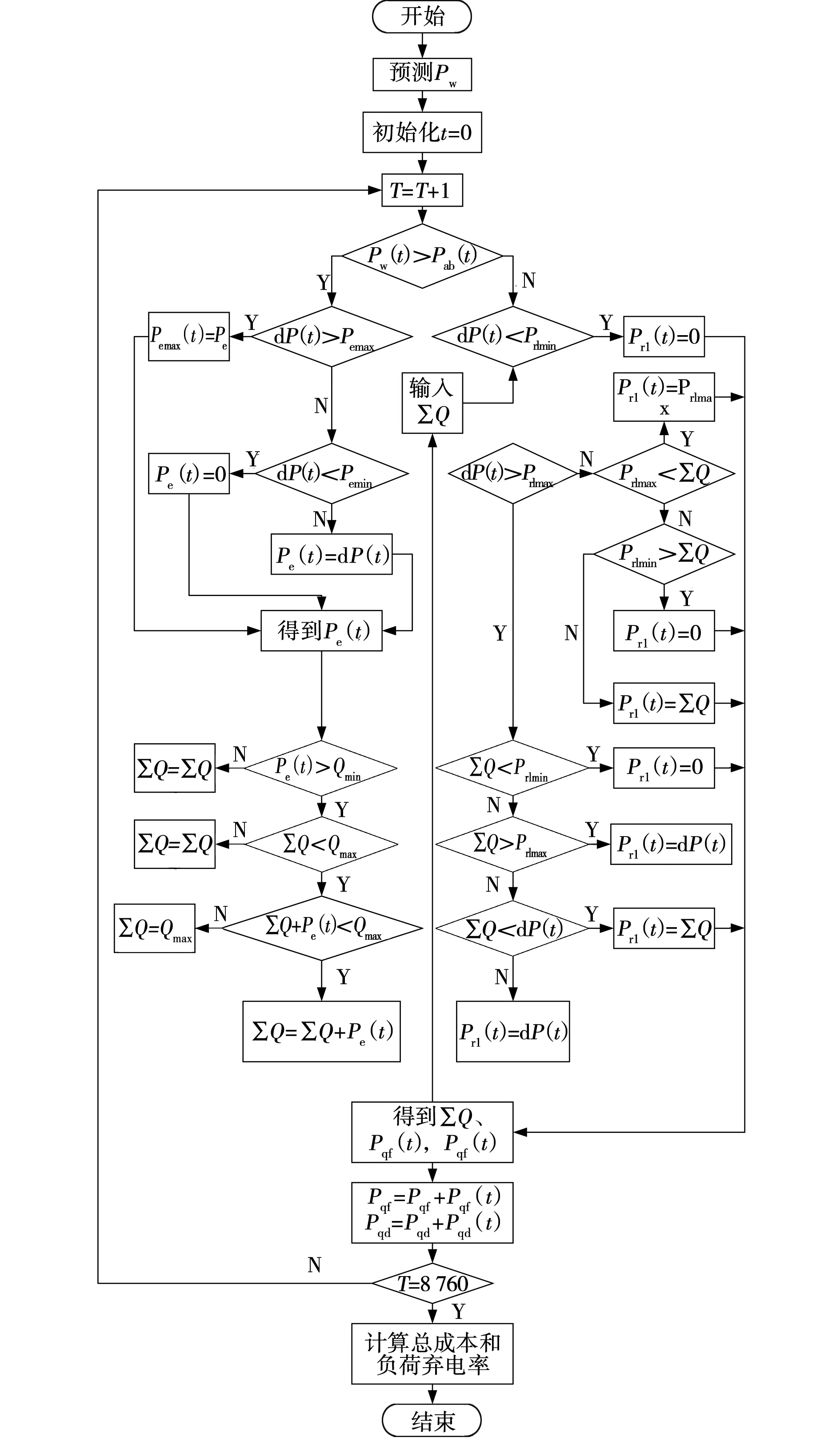
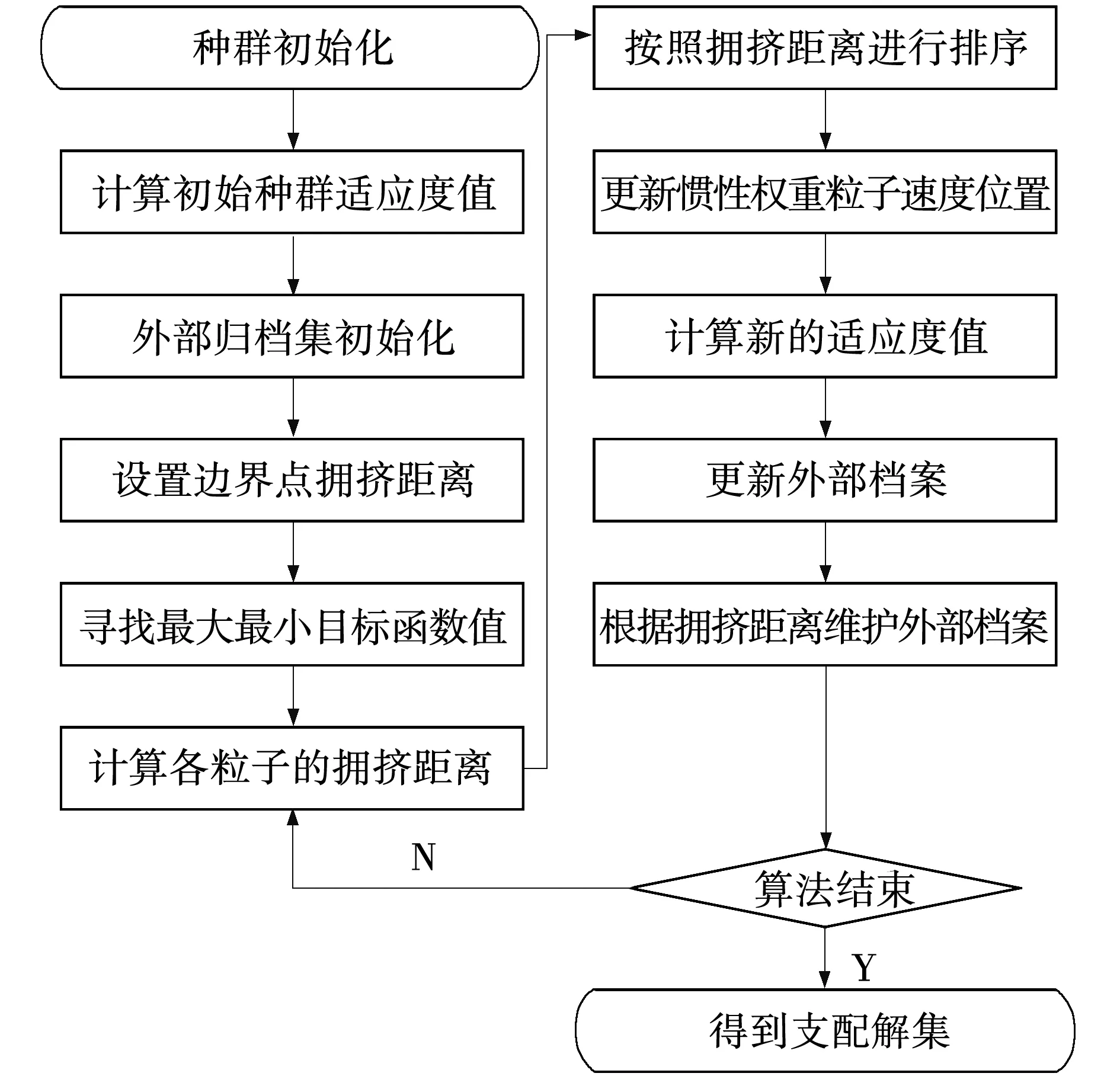
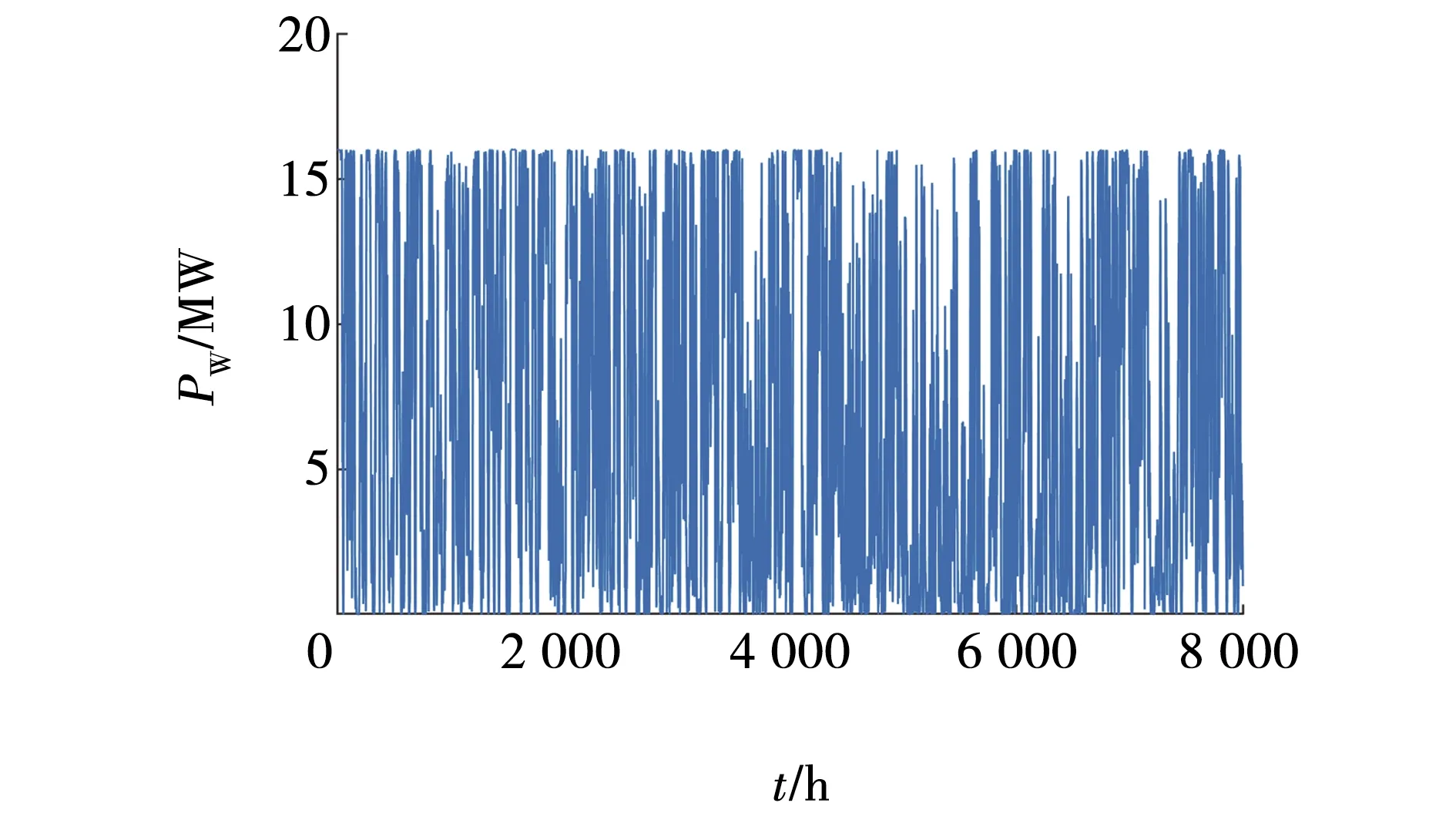
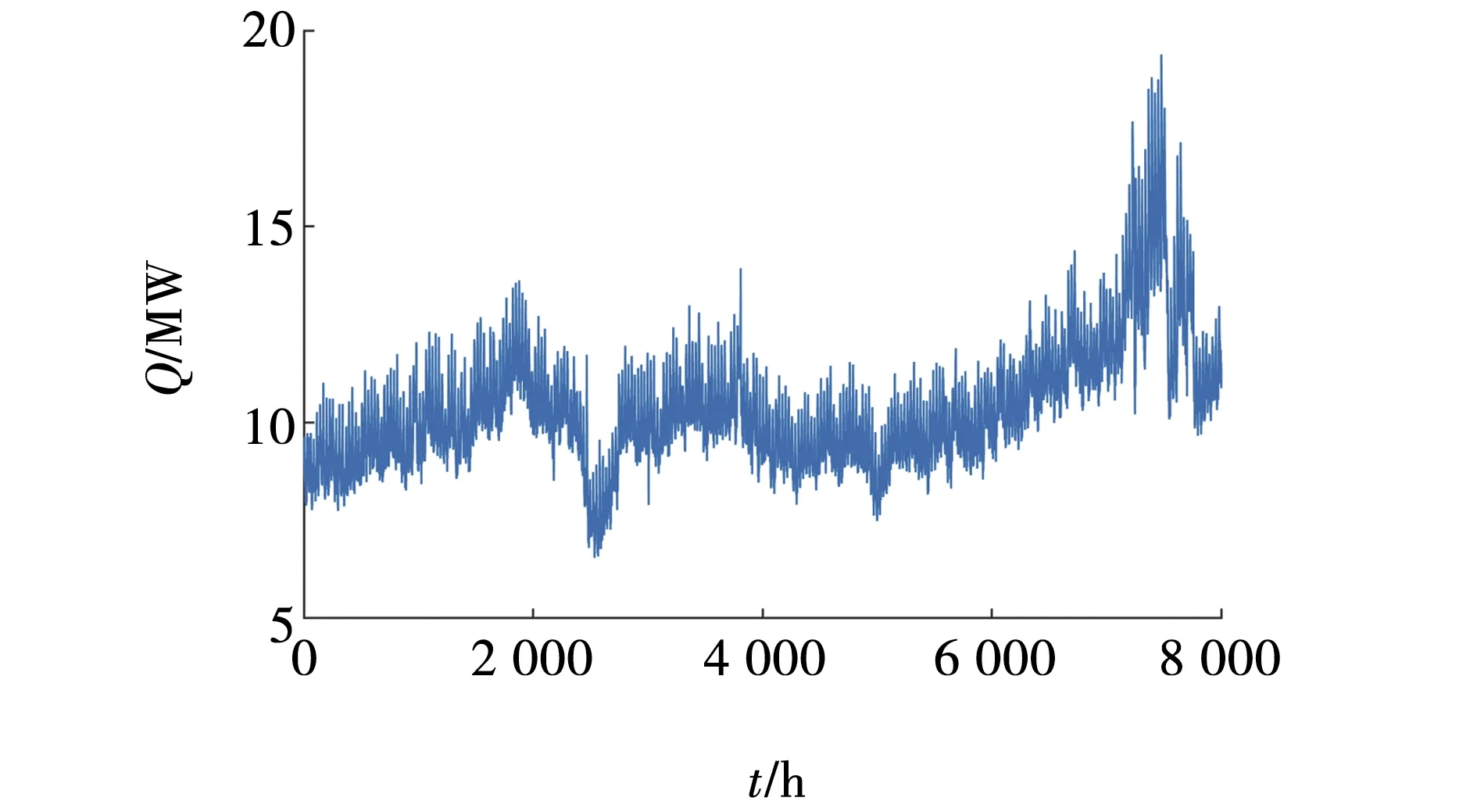
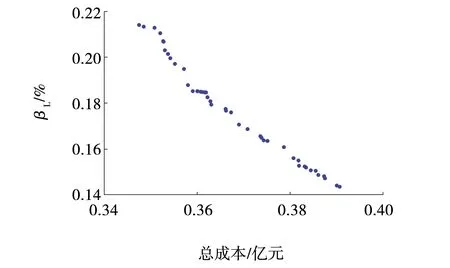
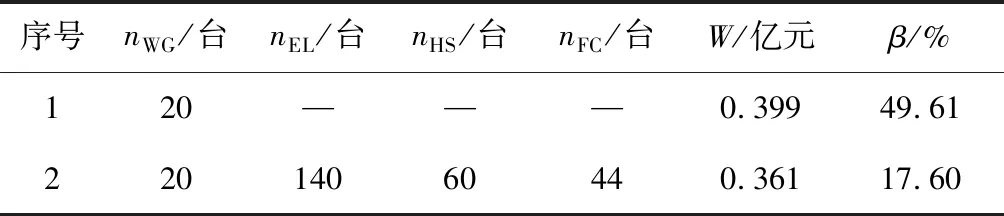
0.2 (3) 3.2.3 各装置的容量约束 以各装置容量作为优化变量,为体现结果的合理性,对各个单元进行装机容量约束,综合考虑成本与系统可靠性的约束范围为 (4) 式中:Ch——储氢罐的数量; Cr——燃料电池的数量; Ce——电解槽的数量。 风储联合发电系统的运行控制策略决定了各单元发电情况,从而影响优化结果的可靠性。当风电功率大于负荷功率时,多余的风电功率通过电解槽转化为氢气存储在储氢罐中;当风电功率小于负荷功率时,由燃料电池将氢气作为燃料发电,具体策略如图3所示。图中,Pqf(t)、Pqd(t)分别为t时刻的弃风量和弃电量;dP(t)为风电功率与负荷功率的差值;Pemin、Pemax是电解槽产氢功率的最大、最小值;∑Q为储氢罐总储氢量,Qmin、Qmax是储氢罐最大最小储氢容量,Prmin、Prmax为燃料电池最大最小功率。 图3 微电网运行控制策略Fig. 3 Microgrid operation control strategy 将电解槽、储氢罐以及燃料电池的装机容量作为优化函数,建立容量配置优化模型。微网的容量配置优化问题属于多目标非线性问题,鉴于多目标粒子群优化算法具有鲁棒性好、速度快的优点,因此,本节采用多目标粒子群优化算法求解容量的最佳配置方案。具体过程如下:首先,初始化种群规模、速度和位置,计算种群适应度值;其次,根据风电预测功率和实际负荷曲线进行仿真分析;最后,获得非劣解集并计算得到年弃风电量和负荷缺电率。具体流程如图4所示。 图4 容量优化配置流程Fig. 4 Flow of capacity optimization configuration 多目标优化得到的非劣解集,采用单调性分段线性隶属度函数求解最优[11],非劣解集中每个解分别进行隶属度计算,并进行综合隶属度排序,将模糊评价最好的点作为容量配置最优解。 综合隶属度越大,则该解越优,第y个目标函数的第x个解的隶属度为 式中:λx,y——第x个解的第y个目标值; 非劣解集中第x个解的综合隶属度为 式中,n1、n2——目标函数个数和非劣解集中解的个数。 为验证所提容量配置优化模型的有效性与可靠性,以某地风电场数据为算例进行仿真分析。 选取风电功率和负荷数据的时间跨度约为1,数据点数为8 000组,利用所建的风电功率预测模型,对风电功率进行预测,预测结果如图5所示。 图5 风电功率预测值Fig. 5 Predicted value of wind power 微网中所涉及的总负荷数据为8 692 916 kW,日负荷均值为1 087 kW,具体负荷曲线如图6所示。 图6 负荷功率Fig. 6 Load power 系统参数包括风机、电解槽、储氢罐以及燃料电池寿命、装机和运行成本,具体参数如表1所示[12]。 表1 各单元成本 根据所建容量优化配置模型,首先,设置种群规模为100,最大迭代次数为1 000次,随机初始化种群的位置和速度并计算个体适应度值。更新个体最优粒子,根据新粒子支配关系筛选非劣解集,更新粒子速度和位置并重复上述步骤,进行迭代计算,所得的非劣解集如图7所示。 图7 非劣解集Fig. 7 Pareto set 由图7可见,得到非劣解集后,采用单调性分段线性隶属度函数,从解集中找到综合隶属度最高的点,即为最优解,将所得最优解与未加入储能的风电系统进行比对,方案2的经济性和可靠性都明显优于方案1。具体结果如表2所示。表中,nWG为风电机组,nEL表示电解槽,nHS为储氢罐,nFC表示燃料电池,W为系统总成本,β表示系统负荷弃电率。 表2 容量优化结果对比 由表2可知,容量配置优化后的总成本由3 990万元降至3 610万元;总弃电率从49.61%下降到17.60%。结果表明,氢储系统不存在传统储能自放电问题,可实现电能的长期存储。文中所提微网的氢储容量优化方法能够有效应对电网的削峰填谷问题,也有助于降低微网成本、减少负荷缺电率及平抑风电功率波动。 笔者以风储联合发电系统为基础,提出了一种考虑风氢互补的微电网容量优化配置方法。 (1)利用改进的BP神经网络模型预测风电出力,采用多目标粒子群优化算法筛选非劣解集,分析了非劣解集的综合隶属度,给出了在风电机场配置140台电解槽,60台储氢罐以及44台燃料电池的最优方案。 (2)与传统风电场相比,成本降低了3 800 000元,负荷缺电率下降了32.01%,提升了微网的经济性和可靠性。4 微电网控制策略与模型求解方法
4.1 运行控制策略
4.2 模型求解方法
4.3 最优配置方案
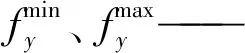
5 算例分析
5.1 仿真场景
5.2 参数设置

5.3 容量优化配置结果
6 结 论
