模糊C均值聚类算法的冲击地压危险等级预测
2021-06-04武俊峰成燕峰梁燕华郭旭飞
武俊峰,成燕峰,梁燕华,张 芳,郭旭飞
(1.黑龙江科技大学 电气与控制工程学院, 哈尔滨150022; 2.哈尔滨理工大学 自动化学院, 哈尔滨150080)
0 引 言
冲击地压是一种对煤矿安全有重大威胁的煤岩动力灾害[1]。尹增德等[2]在对冲击地压预测研究中提出,冲击地压受多个非线性因素影响,传统的预测方法有很大的局限性。研究冲击地压预测,确定各指标的危险等级及危险指数非常重要,其涉及冲击地压指标的模糊集合划分。传统的冲击地压危险等级确定方法依据现有经验知识,需要煤矿方面的专家进行鉴定,造成对经验知识有极大的依赖性,且容易出现较大误差。模糊C均值聚类(FCM)算法对分析数据实际分布情况研究尤为突出。刘志国[3]在对模糊C均值聚类算法研究中指出,将物理或抽象对象的集合分组成多个类的过程称为聚类。聚类分析是统计学的一个分支[4],在对数据分析方面起着重要的作用。聚类算法主要用于对大量数据分析处理上[5],而冲击地压的研究恰好与之对应。严加展等[6]指出,聚类分析与模糊理论相结合,更符合实际的数据分布情况。常赟杰等[7]研究表明,FCM算法是一种基于目标函数的聚类算法,聚类过程与带约束的优化问题相类似。刘来权等[8]指出,FCM算法是一类无监督学习的算法,将数据点归入相似类之中。
由于FCM算法相较与其他算法简单,在计算机上容易实现,与K均值聚类算法不同,具有模糊性以及不确定性,更加适合于实际应用,有着和希尔伯特空间构造紧密联系的目标函数,相比于其他目标函数拥有更严密的数学根基。笔者使用模糊C均值聚类算法确定冲击地压指标的模糊区间及其危险等级,建立标准模型库,将新数据通过模糊模型识别中欧氏贴近度方法与标准模型库匹配,预测冲击地压危险,解决冲击地压危险等级的确定对经验知识的依赖性,使其更符合实际,可靠性更强。
1 冲击地压的预测模型
在对冲击地压预测研究中,其各项评价指标(三轴抗压强度、能量、峰值频率)与危险等级之间均为正相关关系,即随着各指标的评价对象值越高,冲击地压危险等级越高。而对冲击地压预测,判断其危险等级非常重要。
1.1 FCM算法的实现
假设数据集X={x1,x2,…,xn}有p个评价指标和n个评价对象,FCM算法将数据样本集X划分为c类,假设有c个聚类中心H={h1,h2,…,hc},FCM算法模型[6]:
(1)
(2)
式中:uij——隶属度xj属于聚类中心hi的程度;
U——由属于每一个数据样本的程度组成的模糊划分矩阵,U=(uij)c×n;
m——用于调整模糊划分矩阵模糊度的权重指数;
‖xj-hi‖2——样本间的相似性度量。
FCM算法的计算过程[7]可以描述如下:
(1)给定固定聚类数c,模糊系数m(通常从1.5到2.5),最大迭代次数T;阈值η(通常从0.001到0.010),初始化模糊划分矩阵,满足式(2)。
(2)根据式(3)更新集群中心H={h1,h2,…,hc},
(3)
(3)根据式(4)更新模糊划分矩阵U=(uij)c×n,
(4)
(4)计算目标函数J(X,U,H)。若J(X,U,H)≤η或者迭代次数已经达到最大值T,算法停止并输出结果,否则重复步骤(2)。
1.2 欧氏贴近度预测冲击地压
采用模糊识别的方法将一组新数据g1×s与FCM算法得到的聚类中心Vc×s相匹配,得出g1×s所属的冲击地压危险等级。为了确定g1×s与Vc×s中哪一个最贴近,需要对其贴近度进行比较。贴近度是两个模糊向量接近程度的度量。设μkh是模糊向量的贴近度,满足μkh∈[0,1],当μkh越小,2个模糊向量越疏远,反之则越接近。计算新数据g1×s和标准模型库Vc×s的贴近度,选其贴近度最大值,对应的冲击地压危险等级即为预测等级。
欧氏距离dkh计算公式为
(5)
式中:s——指标数;
xig——待测样本g的第i个属性归一化值;
xih——第h类样本中心向量的第i个属性归一化值。
贴近度μkh计算公式为
μkh=1-dkh。
(6)
2 实验结果与仿真
2.1 数据采集
通过实验采集数据,实验样品取自煤矿具有冲击倾向性的岩石。实验设备是由SH-Ⅱ声发射系统以及ROCK600-50三轴实验仪组成,设备如图1所示。实验的固定静水压力为5 MPa,ROCK600-50三轴实验仪加载速度为1.5 MPa/min,SH-Ⅱ声发射系统传感器的频段设为20~110 kHz,数据每1 μs采集一次,门槛值为40 dB。

图1 实验设备Fig. 1 Experimental equipment
2.2 冲击地压仿真及预测结果
利用FCM算法[8]对影响冲击地压的抗压强度、能量、峰值频率划分危险等级,确定各指标的危险等级以及其对应的模糊集合,再运用模糊模型识别中贴近度的方法与模型库相匹配,预测冲击地压危险程度。每个指标均选取150个实验数据作为研究对象。
由于各影响冲击地压的指标衡量单位有差异,且数量级差别很大。因此,对其进行归一化处理非常重要,可避免小数值信息被掩埋于大数值样本里,归一化处理公式:
(7)
式中:Xk——为指标值;
Xmax——指标最大值;
Xmin——指标最小值。
根据式(7)对三轴抗压强度σ、能量E、峰值频率f数据归一化处理后,归一化三轴抗压强度σg、归一化能量Eg、归一化峰值频率fg结果,如表1所示。
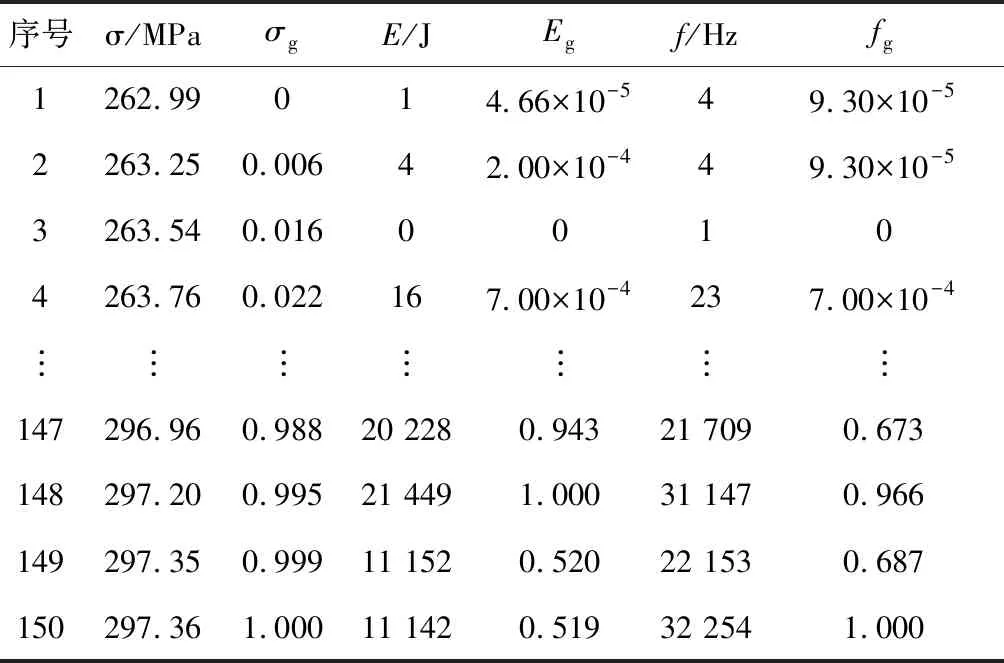
表1 归一化处理数据
通过Matlab软件对三轴抗压强度、能量、峰值频率进行FCM算法的仿真及贴近度预测实验,选前140组数据进行FCM算法分类实验[9-11],建立标准模型库,后10组数据中随机选取一组数据作为测试数据。将冲击地压分为四个危险等级,分别为无冲击危险、弱冲击危险、中等冲击危险、强冲击危险,因此,FCM算法的固定聚类数c=4。令模糊系数m=2,该参数会影响FCM算法的性能;最大迭代次数T=100,阈值η=0.001,若FCM算法对指标数据重复计算100次或者聚类误差小于0.001,获得最优结果。
2.2.1 三轴抗压强度
抗压强度仿真结果数据见图2,σ1表示三轴抗压强度归一化数据,σ6表示聚类中心,σ2、σ3、σ4、σ5分别表示聚类中心所对应的数据集。
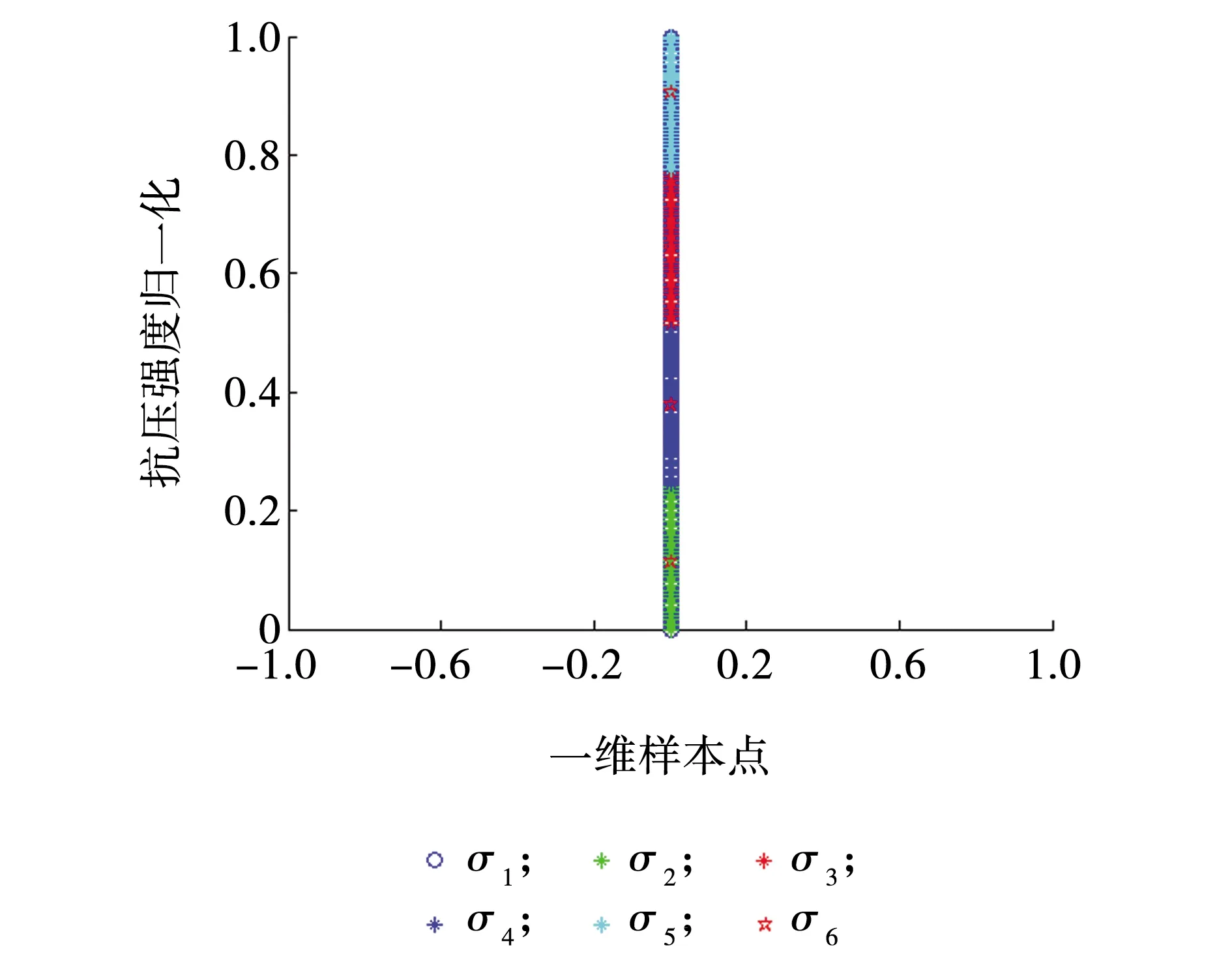
图2 抗压强度仿真结果Fig. 2 Compressive strength simulation result
聚类中心为σ6=[0.114,0.377,0.644,0.907];其中,数据集σ2对应冲击地压危险等级为无危险,根据数据集确定模糊集合为[0,0.24];数据集σ3对应冲击地压危险等级为弱危险,根据数据集确定模糊集合为(0.24,0.50];数据集σ4对应冲击地压危险等级为中等危险,根据数据集确定模糊集合为(0.50,0.77];数据集σ5对应冲击地压危险等级为强危险,根据数据集确定模糊集合为(0.77,1.00]。
2.2.2 能量
能量仿真结果数据见图3,E1表示能量归一化数据,E6表示聚类中心,E2、E3、E4、E5分别表示聚类中心所对应的数据集。
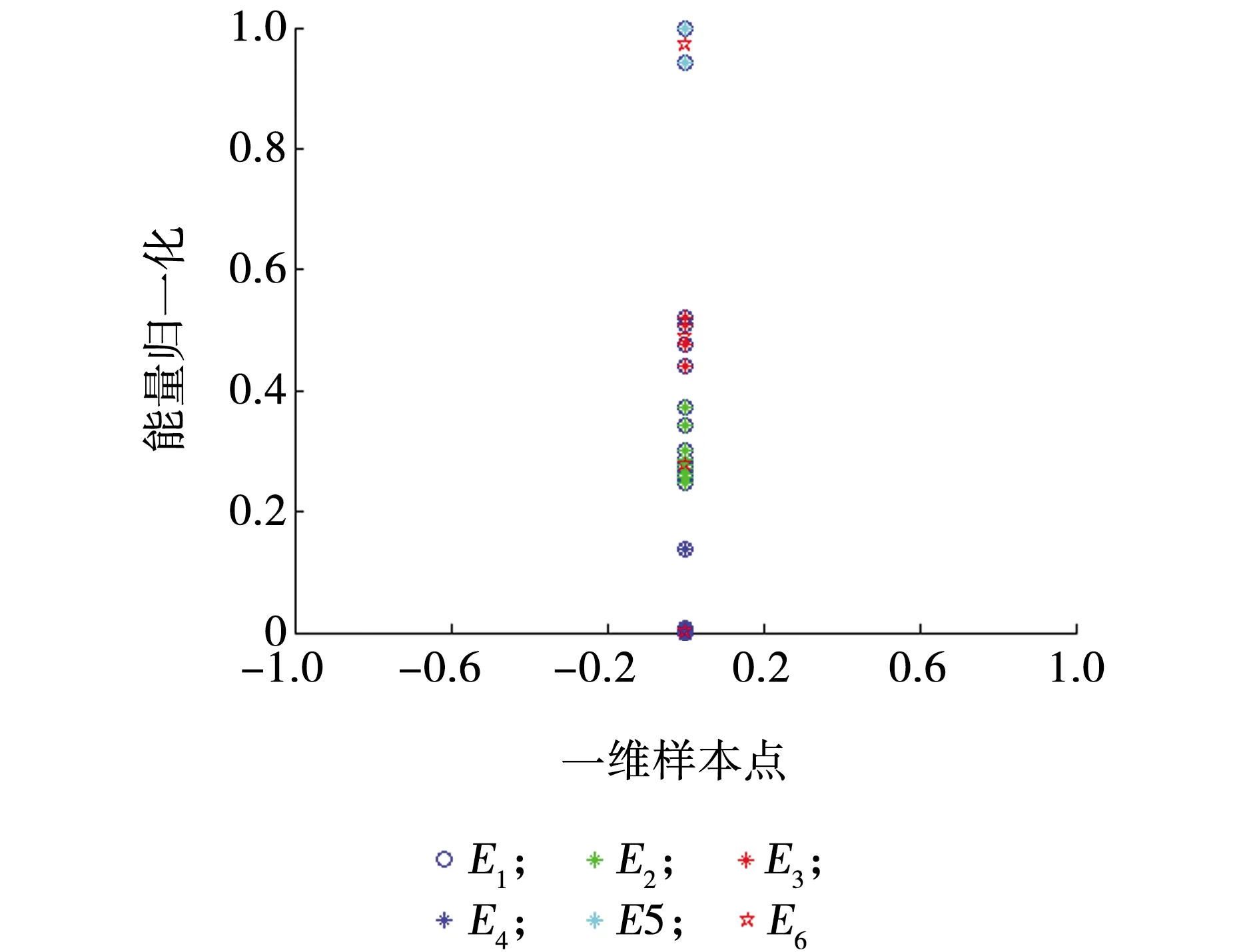
图3 能量仿真结果Fig. 3 Energy simulation result
聚类中心为E6=[0.001,0.277,0.489,0.971];数据集E2对应冲击地压危险等级为无危险,根据数据集确定模糊集合为[0,0.01];数据集E3对应冲击地压危险等级为弱危险,根据数据集确定模糊集合为(0.01,0.37];数据集E4对应冲击地压危险等级为中等危险,根据数据集确定模糊集合为(0.37,0.60];数据集E5对应冲击地压危险等级为强危险,根据数据集确定模糊集合为(0.60,1.00]。
2.2.3 峰值频率
峰值频率仿真结果数据见图4,f1表示峰值频率归一化数据,f6表示聚类中心,f2、f3、f4、f5分别表示聚类中心所对应的数据集。
聚类中心为f6=[0.001,0.271,0.645,0.939];数据集f2对应冲击地压危险等级为无危险,根据数据集确定模糊集合为[0,0.04];数据集f3对应冲击地压危险等级为弱危险,根据数据集确定模糊集合为(0.04,0.40];数据集f4对应冲击地压危险等级为中等危险,根据数据集确定模糊集合为(0.40,0.70];数据集f5对应冲击地压危险等级为强危险,根据数据集确定模糊集合为(0.70,1.00]。
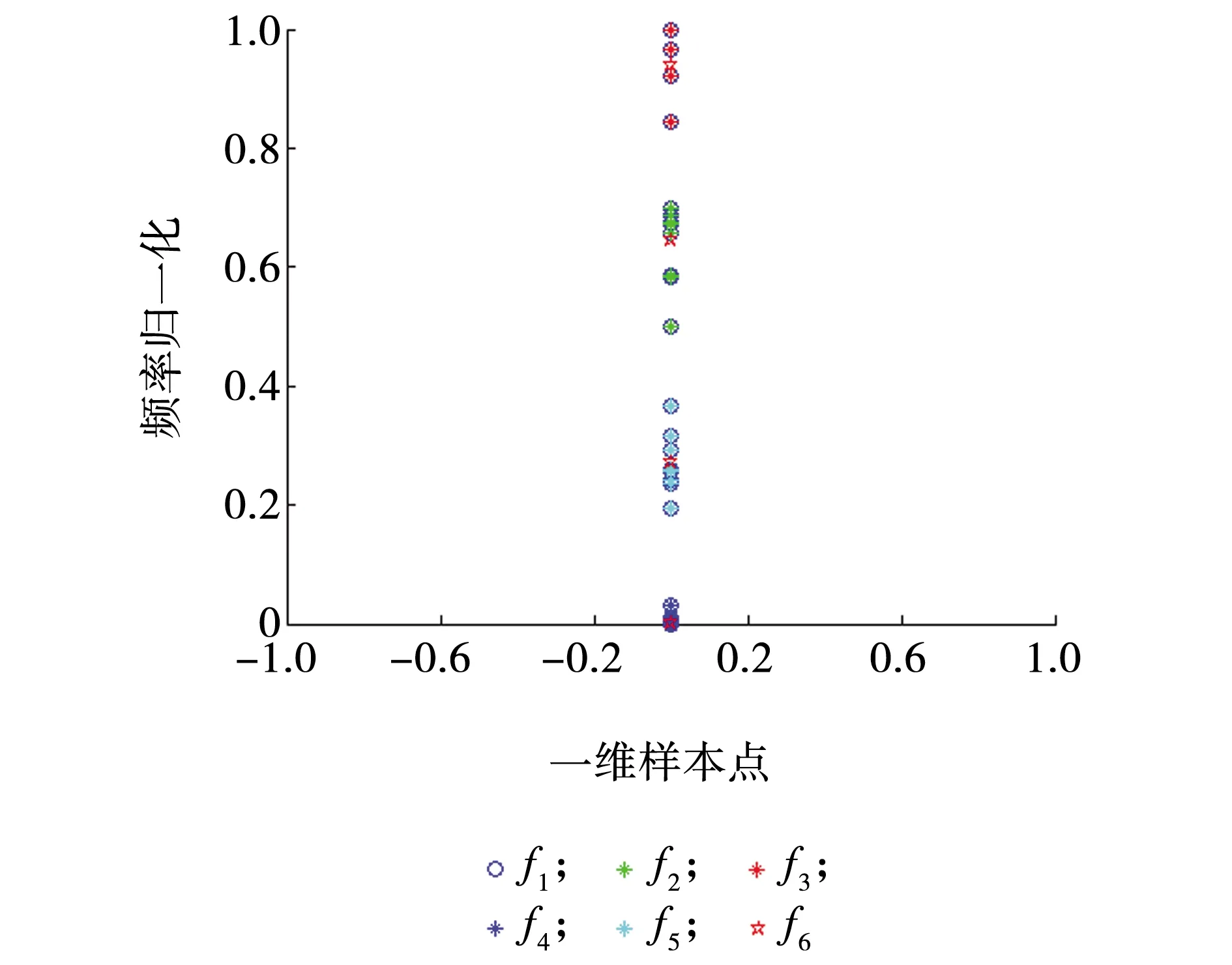
图4 峰值频率仿结果Fig. 4 Simulation resule of peak frequency
由三轴抗压强度、能量和峰值频率的仿真可得,标准模型库为
随机选取一组新数据
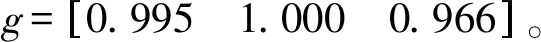
3 结 论
(1)采用FCM算法研究了冲击地压各指标数据的分布,得出应力与声发射中最具代表性的特征抗压强度、能量、峰值频率作为表征冲击地压指标,确定了危险等级划分以及与之对应的模糊区间,为预测冲击地压提供了理论参考。
(2)结合FCM算法和欧氏贴近度,解决了冲击地压危险等级确定对经验知识的依赖性。该模型预测对象的冲击地压危险等级,最大贴近度值为0.944,确定其危险等级为强冲击危险,与实际相符,说明该模型可靠性强,可以有效预测冲击地压。
