脉冲响应字典架构的薄层谱分解方法

李雪英，王福霖，万乔升

(1.东北石油大学 地球科学学院， 黑龙江 大庆 163318； 2.黑龙江省油气藏形成机理与资源评价重点实验室， 黑龙江 大庆 163318)

0 引 言

谱分解，也称时频分析或谱估计，是一种基本的信号分析工具，其目的在于揭示地震记录的时频特征[1]。谱分解通过将一维时域信号变换到二维的时频谱中，描述频率随时间的变化规律。短时傅里叶变换、连续小波变换、S变换和魏格纳威利分布等传统的谱分解方法均受到海森堡测不准原理的限制[2]。

Chen等[3]提出基追踪算法，通过稀疏约束反演，在谱分解中表现出优异的精度和稳定性。Portniaguine等[4]提出将谱分解作为一种反演问题去解决，比较了不同反演约束条件下的时频谱，得出稀疏约束具有最高时频分辨率的结论。目前，基于基追踪的谱分解已广泛应用于微地震数据处理[5]、衰减估计[6]和薄层分析等领域[7]，在地震勘探中，薄层及薄互层的研究一直是一个难点问题。薄层是指厚度小于入射子波λ/8的层状介质，考虑噪音、地震波衰减等因素，薄层被重新定义为小于λ/4的层状介质[8]。薄层是地层中最简单的一种地质结构，但却是研究薄互层地震特征响应的重要基础，深入了解薄层和薄互层的地震响应特征，尤其是时频域响应特征，对提高薄层分辨率、开展薄层预测具有重要意义。

利用基追踪进行谱分解的过程中，尤其研究薄层方面，其字典原子多采用Ricker或Mallet子波，通过褶积模型进行实验[9-13]，但褶积模型所能表征的最小薄层厚度为一个采样间隔，尚不能与地层厚度精确匹配，同时该模型忽略地震波在传播过程中的频散与衰减效应，不能完全模拟地震波在地下介质中真实的传播情况[14-18]。因此，以波动方程为基础，基于波场延拓开展薄层、薄互层正演模拟，研究薄层反射复合波可能更具实际意义[8]。

笔者基于波场延拓理论，利用深度域相移法对不同厚度单砂层和等厚薄互层进行正演模拟，研究各个主频Ricker子波激发的层界面脉冲响应，截取其有效部分，归一化处理后作为原子，构建脉冲响应字典，利用基追踪算法对理论合成的薄层反射复合波进行谱分解，验证该方法对薄层时频分辨率的改善情况。

1 基追踪原理

2004年，Portniaguine等[4]提出地震记录可以表示成一系列小波和相应的系数褶积之和：

(1)

式中：Nb——小波的数量；

t——时间；

n——小波的尺度，该参数控制着小波频率。

式(1)改写为矩阵：

(2)

式中：ψN——主频的卷积矩阵；

Φ——字典，其每一列被称为原子；

η——随机噪声；

α——字典对应的系数序列向量，其中包含了地震记录s(t)的时频分布信息。

将上述α系数序列向量按频率重列成t×n的矩阵，即为时频谱。求解最稀疏系数序列α本质上是寻找地震信号最稀疏表达，该问题可以表示为

(3)

式中，‖α‖0——系数序列向量中非零元素的数目。

由于字典Φ是过完备的，因此使用式(3)求稀疏分解的结果是NP-Hard问题。Chen等提出基追踪算法[3]来解决信号稀疏表示的问题，基追踪基于全局优化算法来实现稀疏表示的问题，其求解模型为

(4)

用l1范数代替l0范数的微妙差异改变了问题的性质，将NP难问题转化成基追踪问题，而基追踪问题可以变形为线性规划问题从而求解。基追踪算法的主要创新于基于线性规划理论，通过最小化l1范数求解系数向量，将稀疏分解转化为约束极值问题。 Donoho进行的实验证明，基追踪算法不仅可以使用尽可能少的原子实现原始信号的表示，而且可以获得比匹配追踪更稳定的结果。

将基追踪算法转化为线性规划问题即可得到稀疏约束下的精确解，进而求得系数序列α。此外，投影梯度法、对偶对数障碍规划算法等都是有效的求解方法。除算法外，预定义的字典也很大程度上影响算法求解精度[2]。

采用波动方程正演模拟的单界面脉冲响应信号，制备了全新的脉冲响应字典，以式(4)为稀疏反演框架，采用线性规划算法获取薄层、薄互层的系数序列矩阵。

2 脉冲响应字典的制备与地质模型

2.1 脉冲响应字典制备

基于脉冲响应字典架构的谱分解方法是用人为构建的脉冲响应字典实现地震信号的谱分解，其核心在于脉冲响应字典的构建。三种不同子波的时域波形如图1所示。

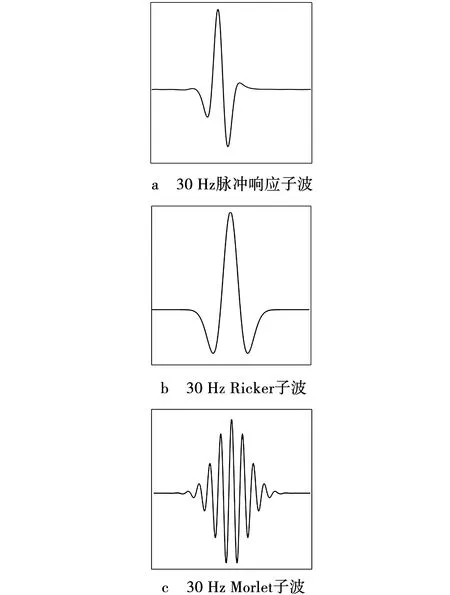
图1 三种不同子波的时域波形 Fig. 1 Time-domain waveforms of three different wavelets

建立单反射界面模型，界面上下的厚度均为3 000 m，其中砂岩的速度为2 918 m/s，密度为2.14 g/cm3；泥岩的速度为3 180 m/s，密度为2.32 g/cm3(全文模型参数与此一致)。

基于波场延拓理论，应用深度相移法正演模拟获取单界面地震响应。采用零相位雷克子波作为激发震源，激发主频以1 Hz为间隔，从1 Hz变化到100 Hz，得到100个不同激发主频的地震反射记录。

此时激发得到的地震记录不是复合波，而是单一界面的脉冲响应，提取中间道的脉冲信号，截取信号的有效部分(图1a)进行归一化处理，以消除信号振幅大小对谱分解结果的影响。将该信号作为脉冲响应字典中的一系列原子，即式(1)中的ψ(t,n)。将其沿着方阵主对角线方向平移构建卷积矩阵ψN。将不同频率的卷积矩阵ψN按频率变化依次排列，组成的矩阵即构成了脉冲响应字典。

ψ1={(ψ(t,1))(ψ(t-1,1))…(ψ(1,1))},ψ2={(ψ(t,2))(ψ(t-1,2))…(ψ(1,2))},…,ψN={(ψ(t,N))(ψ(t-1,N))…(ψ(1,N))},

(5)

式中：()——由脉冲信号构成的列向量；

{}——不同频率的卷积矩阵；

ψ(t-τ,N)——时移量为τ、主频为N的脉冲信号。

需要说明的是，因为脉冲信号都经过归一化处理，所以界面反射系数的大小不影响谱分解结果。文中根据实验需要，构建了频率范围足够宽的脉冲响应字典，在应用中，应根据实际需要设计合适的频率范围。

2.2 地质模型的建立

建立单砂层(双界面)模型，该模型由均匀泥岩背景中包含单砂层组成，单砂层厚度以1 m为间隔，从1 m递增到30 m，以考察不同厚度下，脉冲响应字典的时频谱反演精度。薄层上下泥岩厚度各为3 000 m，使单砂层位于地质模型的中心位置。使用了正演模拟方法和观测系统设置方式[19]，共模拟出30套数据体。

建立等厚薄互层模型，该模型由均匀泥岩背景中包含互层数分别为2、3的砂泥岩等厚地质体组成，用以考察不同互层数对脉冲响应字典下时频谱反演效果的影响。模型参数与观测系统设置方式与上文保持一致。单层厚度以1 m为间隔，从1 m变化至30 m，共模拟出60套数据体。

3 仿真实验

单砂层结构简单，是构成薄互层的基本单元之一，其时频谱简单明了，有助于脉冲响应字典与复Ricker子波字典、实Ricker子波字典时频分析效果的对比。同时，分析单砂层的时频特征，总结规律，对薄互层时频特征的分析有指导作用。

等厚薄互层较单砂层结构复杂，时频谱也相对复杂，有助于判断上述字典在互层构造下分解的精度与稳定性，并进行对比。

文中分别用上述字典对单砂层和等厚薄互层正演模拟信号进行谱分解，对比时频谱，分析脉冲响应字典的优势、划定时频谱频率和位置精度并分析各自的时频特征。

3.1 单砂层模型的时频特征

基于波动方程正演模拟的单砂层合成地震记录时域波形如图2所示。当厚度在1到9 m(λ/8)之间时，波形振幅随厚度的增加线性增大；当厚度在9到19 m(λ/4，地层厚度整数值与对波长的等分不完全对应)之间时，来自顶、底的两个反射波发生相消干涉，复合反射波的振幅随地层厚度减薄而减小，成非线性变化；当厚度在19到37 m(λ/2，图中未画出)时，自顶、底的两个反射波发生相长干涉，随厚度增大，振幅略有减小[25]。

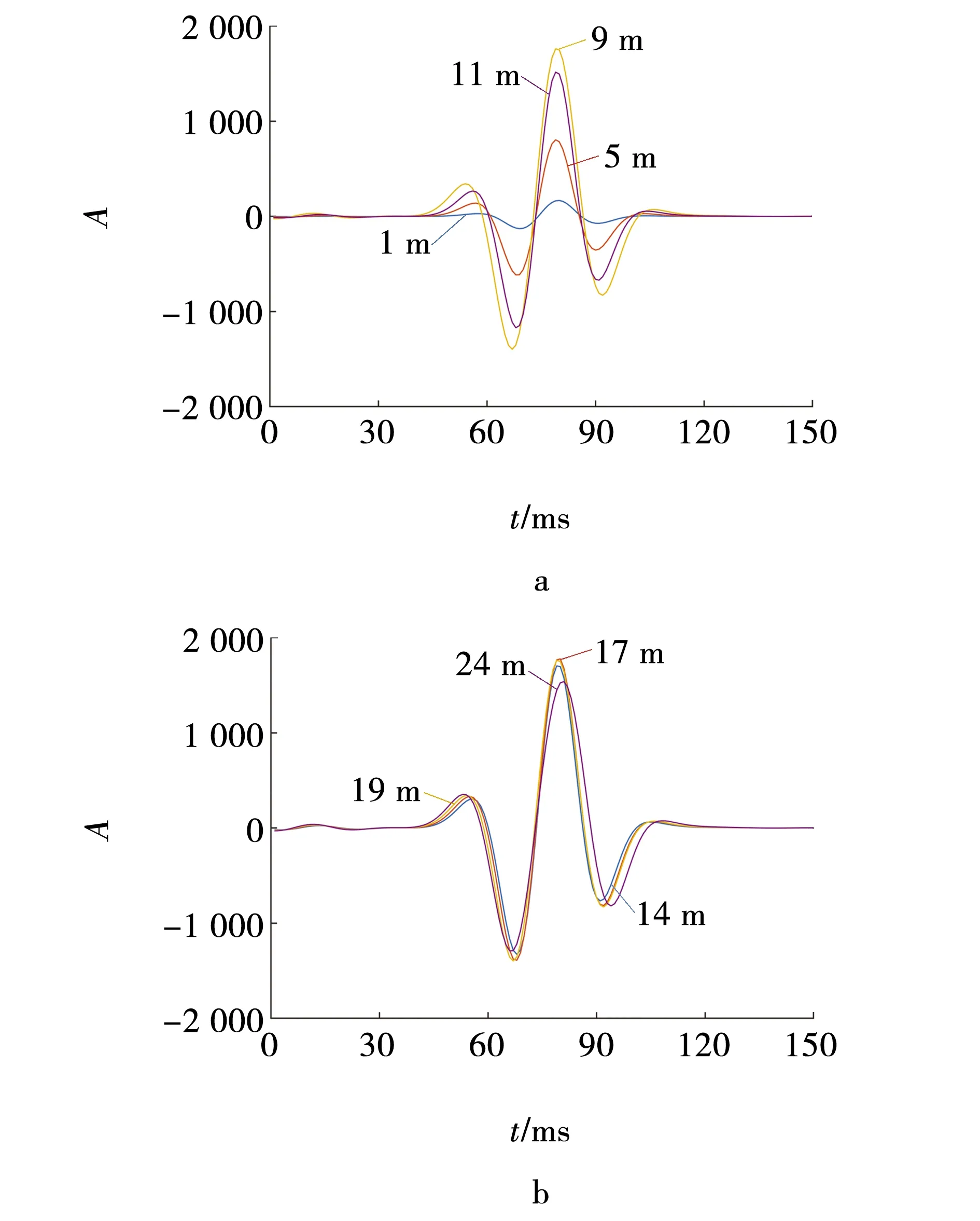
图2 不同厚度的单砂层时域波形 Fig. 2 Time-domain waveforms of single sand layer with different thicknesses

图3为使用复Ricker子波字典对图2时域波形进行谱分解的时频谱，小图内左上方的标识代表层厚度。无论厚度如何变化，频谱均为双峰。受薄层升频特性影响，随着厚度的不断增大，双峰的峰值频率从36 Hz附近下降到30 Hz附近，同时随着相互干涉的两个反射波逐渐分离，基追踪算法求得的解越来越稀疏，使得其频率范围从32～42 Hz缩短到26～32 Hz，频带宽度从10 Hz减小到6 Hz。

当薄层厚度小于λ/4，即厚度小于19 m时，反射波相互干涉程度加剧，波峰与波谷间的频率大于波形主频，能量团双峰向中间高频处聚拢，呈“八”字型分布；当厚度等于λ/4时，能量团近于平行，当厚度大于λ/4，即厚度大于19 m时，干涉程度减弱，波峰与波谷间的频率小于波形主频，能量团双峰向中间低频处聚拢，呈倒“八”字型分布。

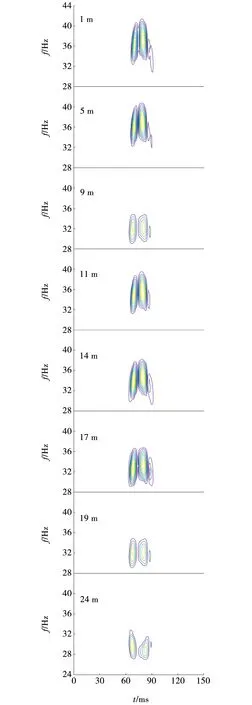
图3 复Ricker子波字典分解的单砂层时频谱Fig. 3 Time-frequency spectrum of single sand layer decomposed by complex Ricker wavelet dictionary

图4为使用实Ricker子波字典对图2时域波形进行谱分解的时频谱。与图3相比，时频谱时间分辨率更高；受薄层升频特性影响，随着厚度的不断增大，双峰的峰值频率从36 Hz附近下降到30 Hz附近；大部分能量团的频带宽度稳定在6 Hz左右。

当薄层厚度小于λ/4，即厚度小于19 m时，能量团呈“八”字型分布；当厚度等于λ/4时，能量团近于平行，当厚度大于λ/4，即厚度大于19 m时，能量团呈倒“八”字型分布。其形成原因与图3相同，但能量的分布形态相较于图3不明显。

图5为使用脉冲响应字典对图2时域波形进行谱分解的时频谱。与图4相比，该图的能量团更为聚焦，出现的位置更为精确，分解出的频率范围更小。无论厚度如何变化，频谱均为双峰(干扰能量团除外)，当厚度在1～19 m之间时，双峰的间距无明显变化，当厚度大于19 m时，双峰的间距随时域复合波的分离而逐渐增加。受薄层升频特性影响，随厚度的不断增大，双峰的峰值频率从34 Hz附近下降到30 Hz附近；单个能量团的频带宽度在2 Hz左右，频率聚焦性比图3和4时频谱提升3倍。由此说明，相比于使用复Ricker子波和实Ricker字典，使用脉冲响应字典对薄层进行谱分解能更精确地识别复合波频率。

当厚度在1～14 m(3/16λ)之间时，时频谱中出现一些干扰能量团，这是薄层厚度过小，复合波时域波形和原子的时域波形不匹配，基追踪算法难以求解出稀疏解所致；当厚度在14～19 m之间时，干扰能量团逐渐消失，时域波形得到了较为精确地时频分解；当厚度大于19 m时，干扰能量团消失，时域波形得以精确分解。能量团发育位置反映时域波形波峰、波谷位置，对应的频率反映时域波形的峰值频率。

当厚度在1～18 m之间时，能量团成正“八”字型分布，当厚度在19 m时，能量团近于平行，当厚度在20～24 m之间时能量团逐渐成倒“八”字型分布。该现象的出现与图3原因相同。此外，时频谱中发育等频的双能量团可局部指示出单砂层结构，这与单砂层是薄互层单元之一的概念是统一的，且当单层厚度大于19m 时，首尾能量团可精确指示单砂层顶底界面位置。

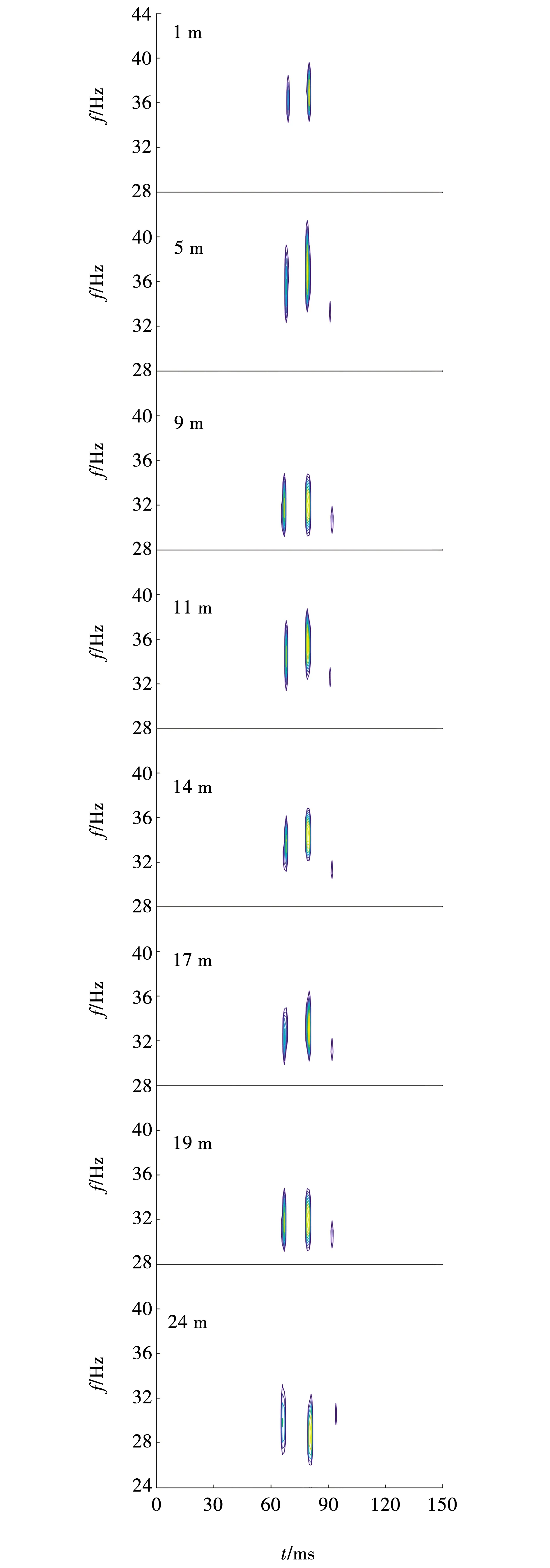
图4 实际Ricker子波字典分解的单砂层时频谱Fig. 4 Time-frequency spectrum of single sand layer decomposed by actual Ricker wavelet dictionary

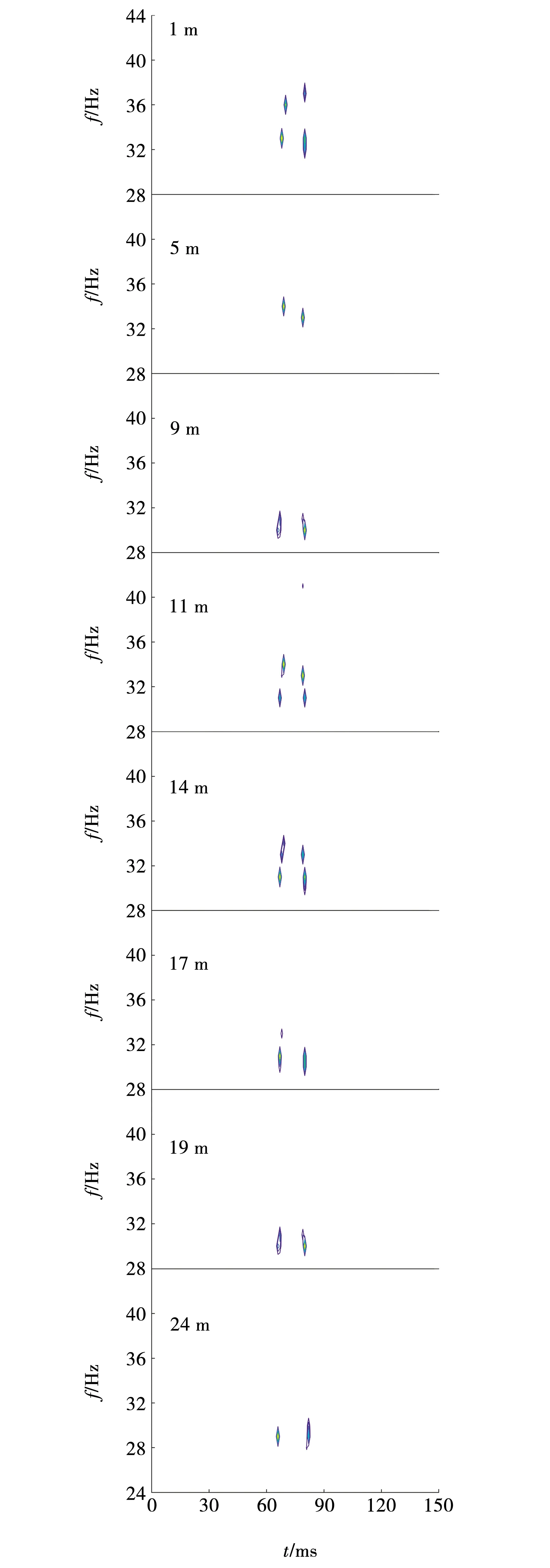
图5 脉冲响应字典分解的单砂层时频谱Fig. 5 Time-frequency spectrum of single sand layer decomposed by impulse response dictionary

3.2 等厚薄互层模型的时频特征

基于波动方程正演模拟的薄互层合成地震记录时域波形如图6所示。

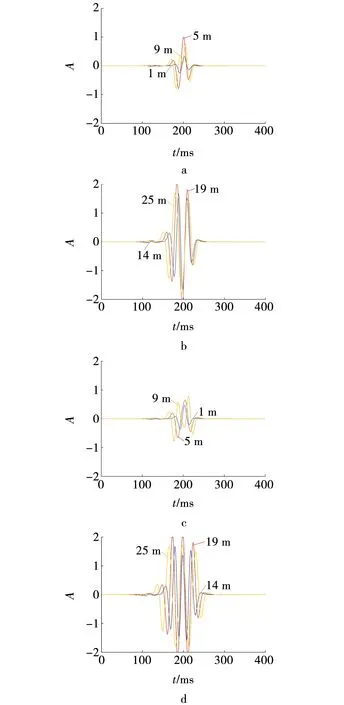
图6 不同互层数、不同厚度的等厚薄互层时域波形Fig. 6 Time-domain waveforms of equal thickness and thin interlayers with different numbers of interlayers and different thicknesses

由图6可见，等厚薄互层时域波形振幅的变化规律与图3相同。

图7和图8为使用复Ricker子波字典对图6时域波形进行谱分解的时频谱。图9和10为使用实Ricker子波字典对图6时域波形进行谱分解的时频谱。

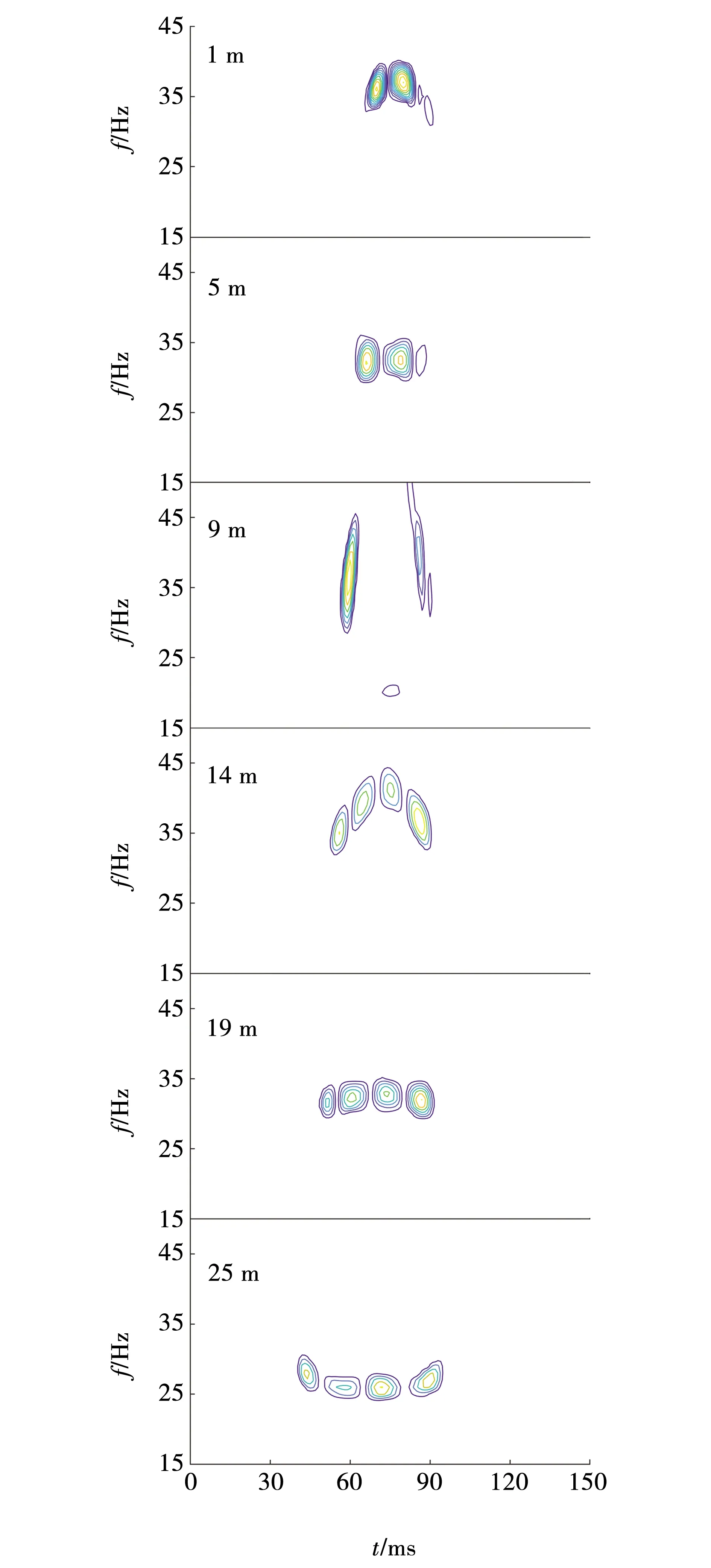
图7 复Ricker子波字典分解的互层数为2的等厚薄互层时频谱Fig. 7 Time-frequency spectrum of equal thickness and thin interlayer with 2 interlayers decomposed by complex Ricker wavelet dictionary

由图7、8可见，当互层数为2，厚度在1～9 m之间时，时频谱表现为双峰；厚度在9～14 m之间时，时频谱峰数由二向四过渡；厚度大于或等于14 m时，时频谱表现为四峰。当互层数为3，厚度在1～5 m之间时，时频谱表现为双峰；厚度在5～14 m之间时，时频谱峰数由二向六过渡；厚度大于或等于14 m时，时频谱表现为六峰。

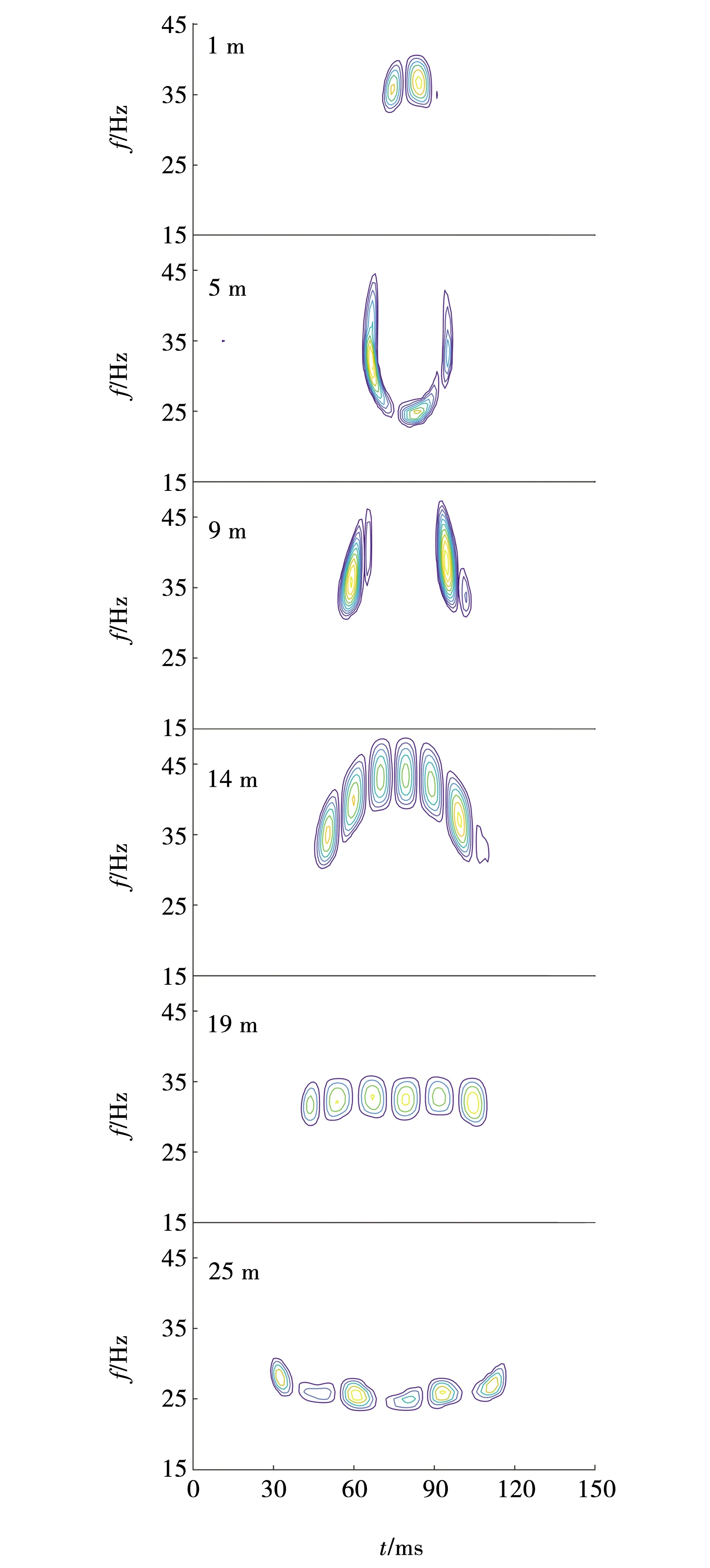
图8 复Ricker子波字典分解的互层数为3的等厚薄互层时频谱Fig. 8 Time-frequency spectrum of equal thickness and thin interlayer with 3 interlayers decomposed by complex Ricker wavelet dictionary

总体上看，受薄层升频特性影响，随着厚度的不断增大，时频谱峰值频率由37 Hz下降到23 Hz，单个能量团的频带宽度大部分在6 Hz左右。

当薄层厚度小于λ/4，厚度小于19 m时，反射波相互干涉程度加剧，波形中间位置的波峰与波谷频率较两侧更高，能量团向高频处移动，呈“n”型分布(5 m例外)；当厚度大于λ/4，即厚度大于19 m时，干扰能量团出现，反射波相互干涉程度减弱，波形中间位置的波峰与波谷频率较两侧更低，能量团向低频处移动，呈“u”型分布。

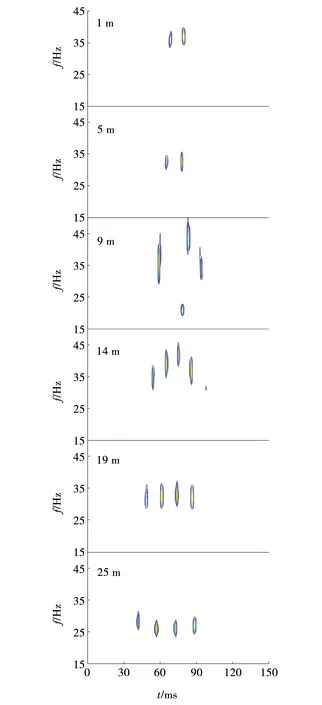
图9 实Ricker子波字典分解的互层数为2的等厚薄互层时频谱Fig. 9 Time-frequency spectrum of equal thickness and thin interlayer with 2 interlayers decomposed by real Ricker wavelet dictionary

薄层厚度小于λ/4，厚度小于19 m，能量团呈“n”型分布(5 m例外)；即厚度大于19 m时，能量团呈“u”型分布。其形成原因与图7和8相同。

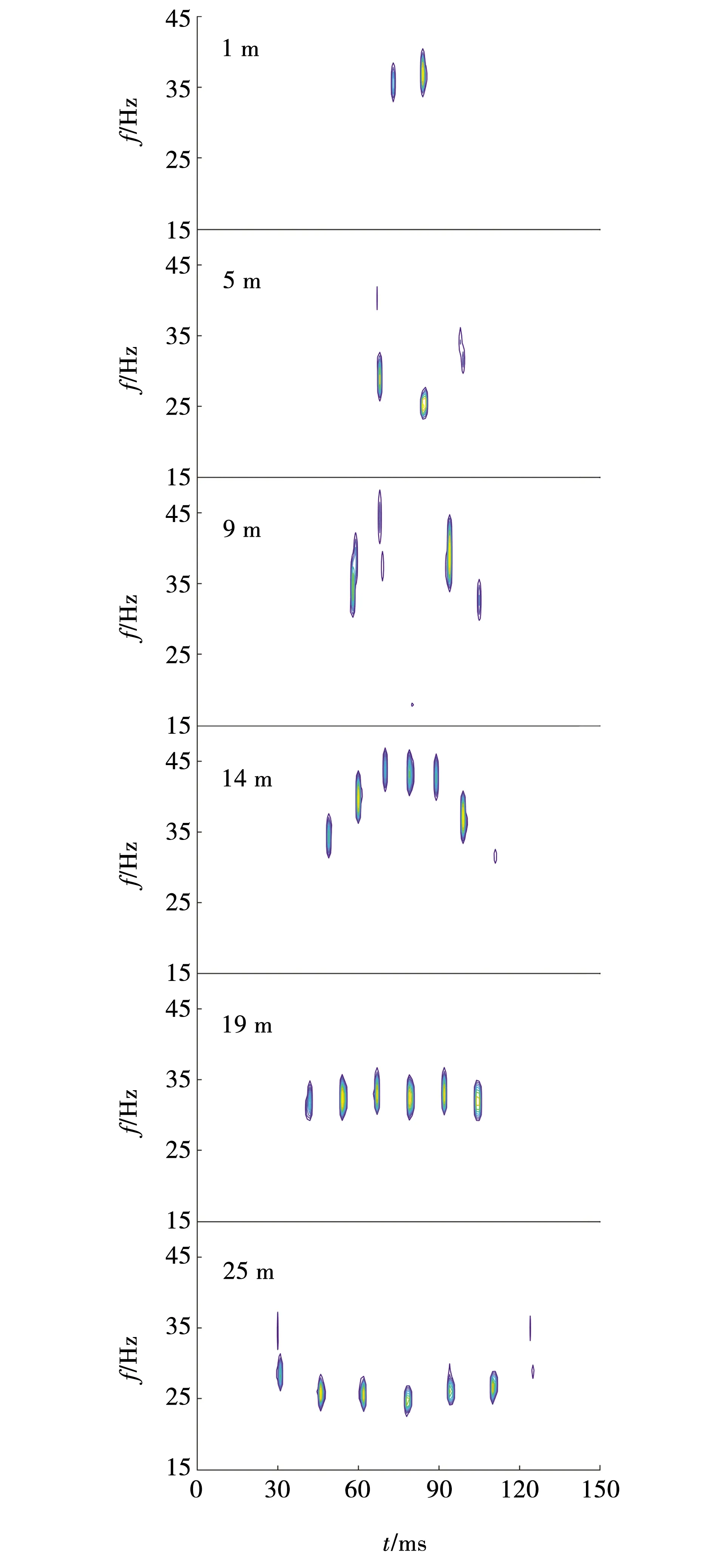
图10 实Ricker子波字典分解的互层数为3的等厚薄互层时频谱Fig. 10 Time-frequency spectrum of equal thickness and thin interlayer with 3 interlayers decomposed by real Ricker wavelet dictionary

图9、10与图7、8相比，时频谱时间分辨率更高。时频谱峰数变化规律与图7和8相同。总体上看，受薄层升频特性影响，随着厚度的不断增大，时频谱峰值频率由35 Hz下降到23 Hz，单个能量团的频带宽度大部分在6 Hz左右。

图11和12为使用脉冲响应字典对图6时域波形进行谱分解的时频谱。

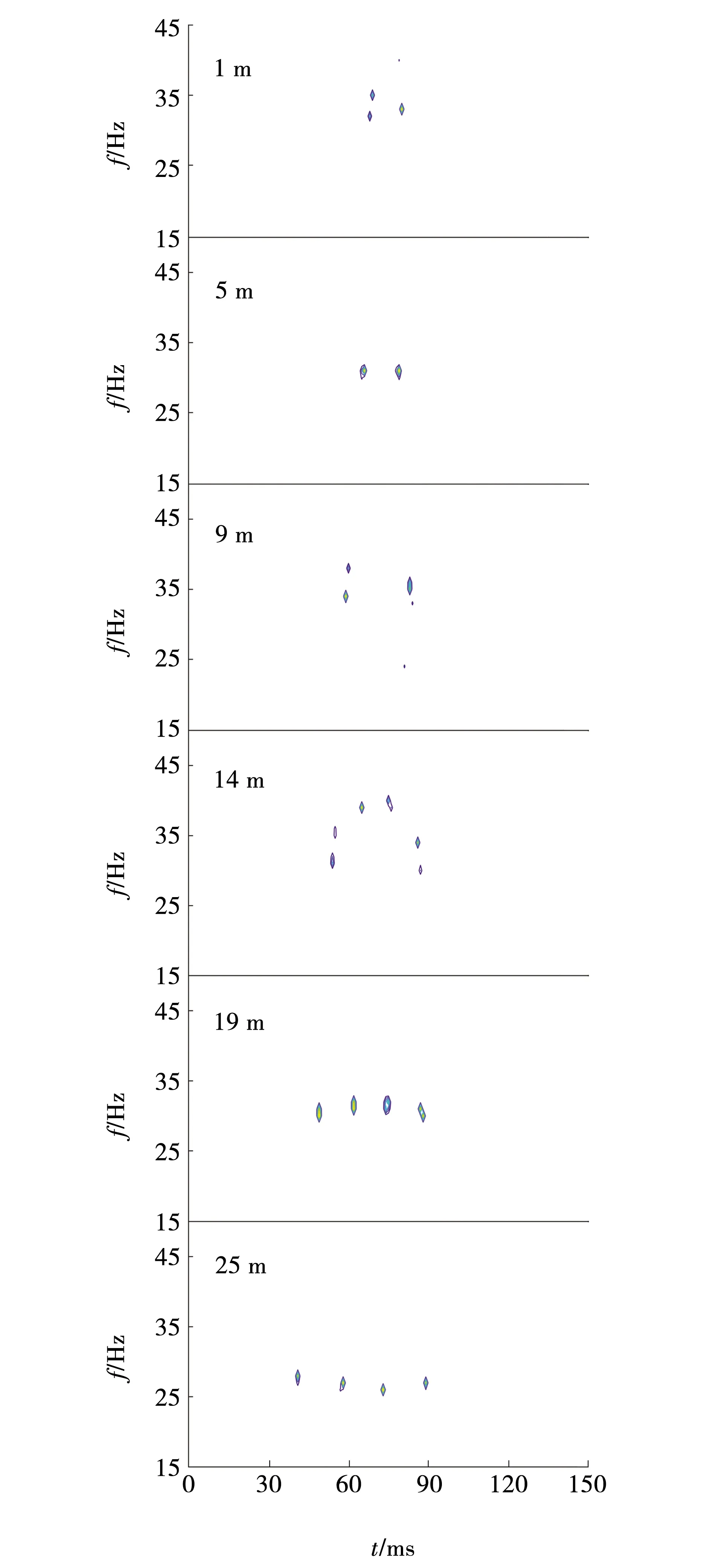
图11 脉冲响应字典分解的互层数为2的等厚薄互层时频谱Fig. 11 Time-frequency spectrum of equal thickness and thin interlayer with 2 interlayers decomposed by impulse response dictionary

图11、12与图9、10相比，能量团更为聚焦，观测到的波形频率更为精确。通过观察可见，当互层数为2，厚度在1～9 m之间时，时频谱表现为双峰；厚度在9～14 m之间时，时频谱峰数由二向四过渡；厚度大于或等于14 m时，时频谱表现为四峰。当互层数为3，厚度在1～14 m之间时，时频谱表现为四峰，并逐渐向六峰过渡；厚度大于或等于14 m时，时频谱表现为六峰。受薄层升频特性影响，随厚度的不断增大，峰值频率从33 Hz下降到23 Hz，单个能量团的频带宽度在2 Hz左右，频率聚焦性比图7和8时频谱提高3倍。由此说明，相比于使用复Ricker子波和实Ricker子波字典，使用脉冲响应字典对薄互层进行谱分解能更精确地识别复合波频率。

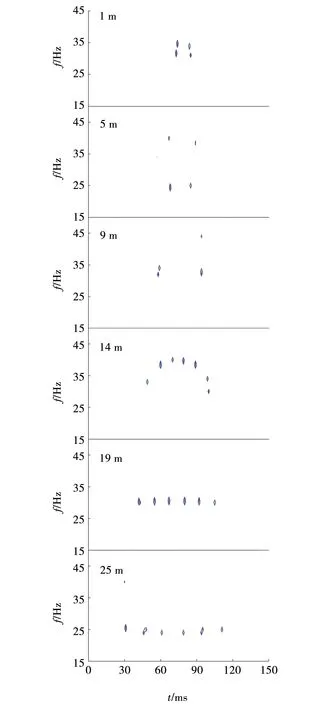
图12 脉冲响应字典分解的互层数为3的等厚薄互层时频谱Fig. 12 Time-frequency spectrum of equal thickness and thin interlayer with 3 interlayers decomposed by impulse response dictionary

当厚度在1～14 m(3/8λ)之间时，时频谱中出现一些干扰能量团，原因与图5相同；当厚度在14～19 m之间时，干扰能量团逐渐消失，时域波形得到了较为精确地时频分解；当厚度大于19 m时，干扰能量团消失，时域波形得以精确分解。能量团发育位置反映时域波形波峰、波谷位置，对应的频率反映时域波形峰频。

当厚度小于19 m时，中间两个能量团向高频处移动，时频谱呈“n”型分布；当厚度大于19 m时，中间两个能量团向高频处移动，时频谱成“u”型分布。其形成原因与图7和8相同。

4 结 论

(1)提出的基于脉冲响应字典架构的基追踪谱分解方法相比于传统的Ricker子波字典谱分解方法具有相同的时域分辨率，且频率聚焦性提升3倍，有利于薄砂层及等厚薄互层时频特性分析。

(2)随着单砂层厚度减薄，时频谱峰值频率逐渐升高，高频能量对薄层分辨能力增强，说明薄的单砂层具有升频特性。

(3)等厚薄互层时频谱能量团由“n”型分布向“u”型过渡，随着单层厚度的减薄，峰值频率逐渐升高，峰值频率数量及间距可清楚展现等厚薄互层内部结构特征。