基于UKPF算法的锂离子电池SOC估算

吴铁洲，刘康丽，杜炘宇

（1.湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，湖北武汉 430068；2.中国市政工程中南设计研究总院有限公司，湖北武汉 430068)

电动汽车具有“零污染”、噪音小、节能等特点，如今已被世界各国大力推广和研究[1]。动力电池作为电动汽车的主要能量来源，对电池组进行可靠的管理和控制，能够在为整车提供所需功率的同时使其达到最佳的性能。由于锂离子电池具有安全性能好、单体电压高、比容量大等特点，将其当成电动汽车的动力来源非常合适。电池管理系统能够实时监测电池工作状态，维持电池单体间均衡，保持整个电池组处于安全稳定工作状态，是电动汽车中不可缺少的一部分。电池的荷电状态(SOC)作为电池管理系统的核心参数之一，SOC的精确度会直接影响到电池的循环寿命和电池管理系统的运行性能[2]。电池SOC对于电动汽车的性能至关重要，但是不能通过直接测量得到。目前SOC估算方法较多[3]，工程上应用最多的是安时积分法，但是安时积分法会引入累计误差，导致精度偏低[4]。因此，许多学者提出以卡尔曼滤波算法[5]为基础的各种电池SOC估算方法，比如扩展卡尔曼滤波法(Extended Kalman filter，EKF)、无 迹 卡 尔 曼 滤 波 法(Unscented Kalman filter，UKF)等。其中UKF 算 法[6]精度最高，但是UKF 算法在估算电池SOC时，将系统噪声统计特性假定服从高斯分布，从而带来精度损失。粒子滤波方法[7]适用性较强，不受限于噪声分布。因此，为了有效解决UKF 算法带来的精度损失问题，本文提出将UKF 算法作为粒子滤波算法的建议分布函数与粒子滤波算法结合，得到无迹卡尔曼粒子滤波(Unscented Kalman Particle filter，UKPF)算法，并用该方法估算锂离子电池SOC。

1 SOC定义

电池荷电状态是电池的重要参数，它所表示的是电池容量的消耗程度，电池管理系统根据SOC值控制电池的工作状态[8]。精确估计SOC值可以有效防止动力电池过充过放，提高整车性能以及经济性。电池SOC受多种因素影响，本文拟采用带系数的SOC计算式对电池SOC进行估算，通过系数来修正SOC值，如式(1)所示。

式中：Q表示电池的标称容量，Ah ；ηi、ηT和ηc分别为充放电倍率、温度和充放电循环次数下对锂离子电池容量的修正系数。

2 锂离子电池建模及参数辨识

常用的电池等效模型有Rint 模型、Thevenin 模型和PNGV 模型等，这些电池模型都有其各自的优缺点。由于本文所采用的算法对于电池模型所造成的误差具有一定的修正，因此在模型选择上可以选择结构简单精度适中的模型，综合考虑后，Thevenin 等效电路[9]模型符合要求，本文将电流传感器测得的电流分为电流真实值Ireal和漂移电流Id，Id是指电流传感器中的测量噪声带来的误差，在Thevenin 等效电路模型的基础上，引入Id，融合成电池混合噪声模型，并用该模型实现锂离子电池SOC估算，电路结构图如图1 所示。

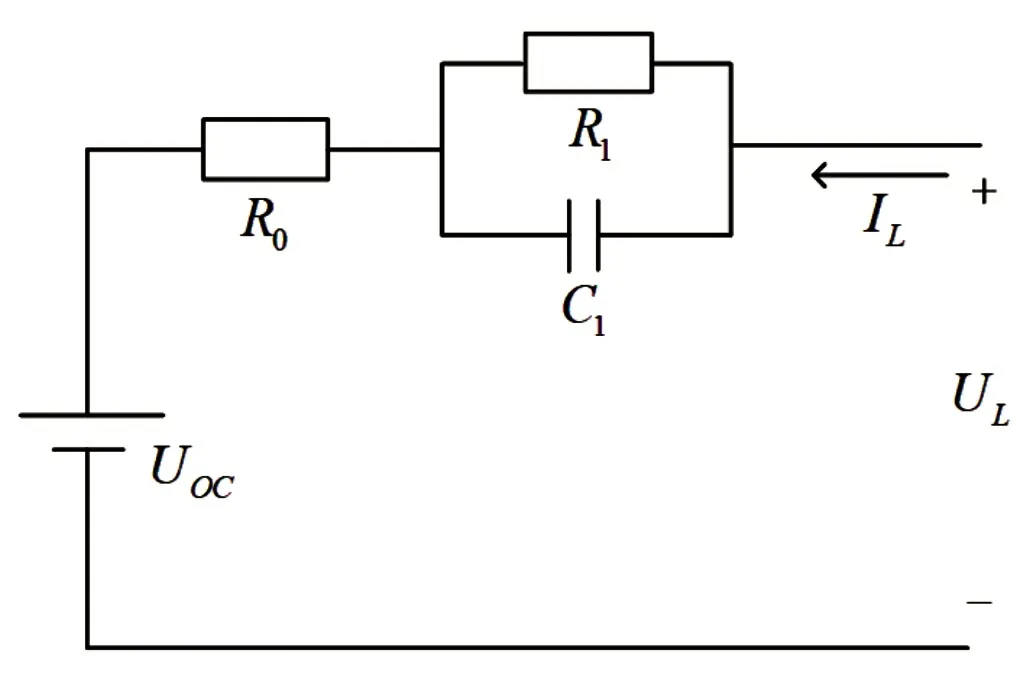
图1 Thevenin 模型电路结构图

根据图1 所示电路图，可以得到模型的数学表达式如式(2)和式(3)所示：

检测到的电流数值用IL表示，IL由真实值Ireal与漂移电流Id组成，如式(4)所示：

将式(4)代入到式(1)～式(3)中，即为电池混合噪声模型的表达式，如式(5)～式(8)所示：

式中：r为零均值高白噪声。

通过相关试验来获取电池等效模型中的参数。充放电试验是为了得到电池SOC与开路电压之间的关系。

首先将试验电池充满电，然后以0.2C放电30 min，静置1 h，测量电压，得到对应当前SOC的电池端电压。重复上述操作，直至电量耗尽。OCV-SOC曲线见图2。

图2 电池OCV-SOC拟合曲线

然后辨识极化电阻、极化电容和电池内阻。

设定环境温度为25 ℃。将电池电量充满。电池电量充满静置2 h，在SOC为1、0.9、…、0.1 处进行HPPC 试验，记录数据。HPPC 充放电电流分别设为0.75C和1C。HPPC 工况试验电流电压示意图见图3。

图3 HPPC 工况示意图

R0的计算可以根据欧姆定律R=U/I得出，I为HPPC 试验时的电流，当电池处于放电状态时U=U0-U1，当电池处于充电时U=U5-U4；根据电路结构以及系统的零输入响应和零状态响应，可以求得R1、C1，根据图2 所示的电流电压变化特性，结合最小二乘拟合即可得到时间常数τ 和极化电阻R1。至此可以获得模型中的各个参数值，见表1。

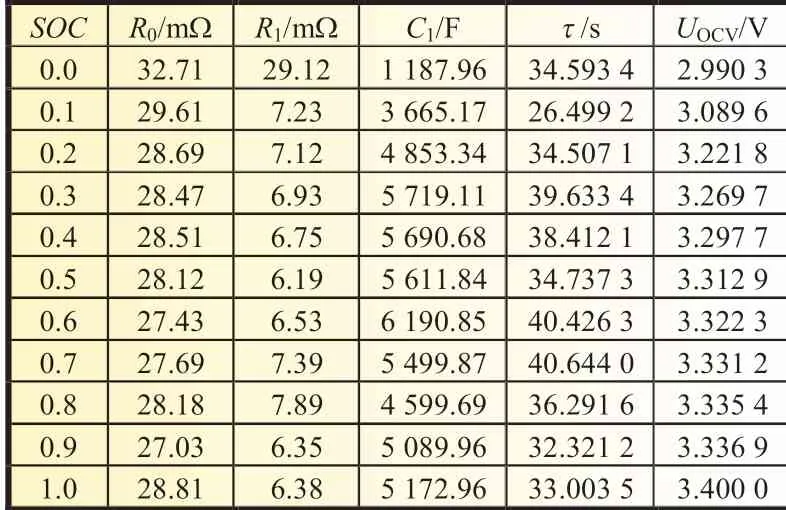
表1 模型参数表

为了获得SOC与电池模型参数之间的关系，本文将上述所得的试验数据导入Matlab 进行五阶多项式拟合，表达式如式(9)所示：

在恒流工况下，采用标称容量为3.3 Ah、标称电压为3.2 V 锂离子电池对所述电池模型精度进行验证。恒流放电电流大小设置为0.5C，环境温度设置为25 ℃，得到的仿真结果见图4 和图5。

图4 恒流放电下端电压估计值与真实值对比

从图4 中可以看出，模型端电压的估计值与真实值非常接近，在试验刚开始时误差最大为0.015 V，由图5 可知，模型误差波动很小，最大相对误差为0.46%，满足锂离子电池SOC估算要求。

图5 恒流放电下端电压估计值误差

3 基于UKPF 的粒子滤波算法

3.1 PF 算法

粒子滤波法[10]通过非参数化的蒙特卡洛(Monte Carlo)模拟方法来实现递推贝叶斯滤波，适用于任何能用状态空间模型描述的非线性系统，由于具有非参数化特点，它摆脱了解决非线性滤波问题时随机量必须满足高斯分布的制约，相较于高斯模型，粒子滤波应用更广泛，建模能力更强。算法示意图如图6 所示[11]。

图6 粒子滤波算法示意图

k-1 时刻，从状态的先验概率分布中随机地取N个等权值的粒子根据似然函数更新粒子权值，得到；然后重采样阶段对粒子和其相应的权值表示的概率密度函数重新进行采样，权值比较大的粒子会被多次复制，那些权值小对计算后验概率函数贡献非常小的粒子就会被剔除，重采样后粒子的权值设为1/N；经过上述步骤后，利用系统的状态转移模型，就可以实时估计粒子的状态。

PF 算法步骤如下：

3.2 UKPF 算法

UKF 算法的核心是UT 变换[12]，用确定的采样来近似状态的后验概率密度，不用对系统模型进行线性化处理，但UKF 仍然是用高斯分布来逼近系统状态的后验概率密度，所以在非高斯情况下，滤波结果有较大误差。粒子滤波方法适用性较强，不受限于噪声分布。为了提高SOC估算精度，本文以UKF 和PF 算法作为基础，将UKF 作为PF 的建议分布，得到UKPF 算法，具体步骤如下所示。

系统的状态空间数学模型如式(12)所示：

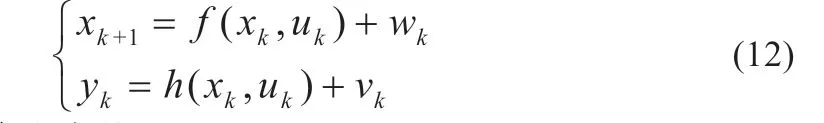
UKPF 算法步骤：

综上可知，UKPF 算法在运行过程中，充分利用最新观测信息，能够很大程度上抑制噪声造成的不利影响。从理论上分析，UKPF 算法精度优于UKF 和PF。

4 实验及结果分析

为验证所提UKPF 算法的有效性，选择如式(24)所示目前国内外广泛使用的数学模型[13]，采用PF、UKF、UKPF 三种算法对式(24)所示的模型进行状态估计，对比三种算法性能。

其中，设定目标初始状态x0=1.0，且服从：p(x0)～N(0,0.75)，取每次仿真的时间步长t=60 s，粒子数N=200。仿真结果如图7 所示，其中UKF 和UKPF 算法中取参数α=1，β=0，k=2。可知，PF 的估计误差较大，跟踪性能不稳定；UKF 在估算过程中误差也比较大，而UKPF 由于充分利用了系统的观测信息，算法的估计结果与真实值比较吻合，精度最高。图8 为每次随机初始化，采用三种滤波算法执行100 次蒙特卡罗仿真试验得到的状态估计误差曲线，定义状态估计的均方根误差如式(25)所示：

图7 仿真结果对比图

图8 状态估计误差曲线对比图

表2 给出了三种算法执行100 次蒙特卡罗仿真试验的结果，以及三种算法100 次试验的平均时长。

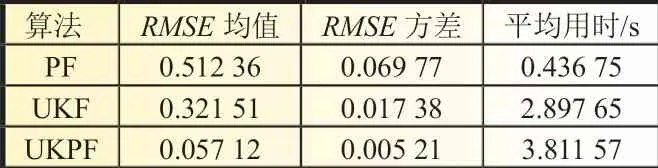
表2 仿真结果

由表2 中数据可得：PF、UKF 算法的RMSE均值和方差较大，UKPF 算法的RMSE均值和方差最小；在运行的时间上，UKPF 算法的运行时间比PF 和UKF 算法稍长。

接下来，为了验证UKPF 算法对锂离子电池SOC估算的精确度，本文采用如图9 所示的试验设备，在NEDC 工况下，采用PF、UKF 和UKPF 算法对锂离子电池SOC进行估算。

图9 试验所用设备

试验对象选择容量3.3 Ah 磷酸铁锂电池，Arbin BT2000控制电池充放电电流，利用恒温箱控制环境温度，PC 机记录电池试验的各种数据。NEDC 工况是目前应用较多的一种工况，本文中其电流如图10 所示，电池所处试验环境温度为25 ℃，SOC初始值为1。仿真结果如图11 所示，算法误差如图12 所示。从图11、图12 中可以看出，基于锂离子电池混合噪声模型的UKPF 算法的误差最小，比PF、UKPF 更稳定，性能更优，最大误差为2.1%，平均误差为0.3%。

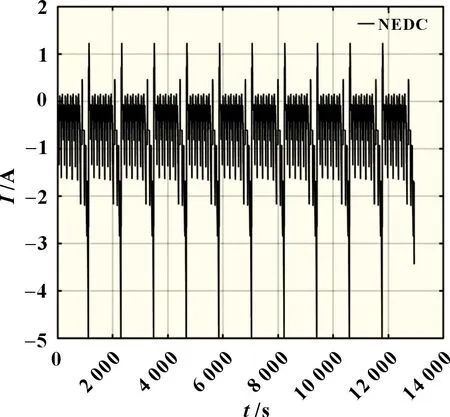
图10 NEDC 工况电流

图11 NEDC工况下三种算法的SOC估算结果

5 结论

电池SOC估算精度对于电动汽车的安全运行而言至关重要。为了提高锂离子电池SOC 估算精度，本文以标称容量3.3 Ah，标称电压3.2 V 的磷酸铁锂电池作为研究对象，基于锂离子电池混合噪声模型，采用UKPF 算法对锂离子电池SOC 进行估计，并与UKF、PF 算法对比，试验结果表明，UKPF算法估算精度最高，最大误差为2.1%，平均误差为0.3%。

图12 NEDC 工况下三种算法的SOC估算误差