船舶结构振动噪声时域预报方法研究

2021-06-03庞福振李海超王雪仁缪旭弘唐宇航

船舶力学 2021年5期

庞福振，李海超，王雪仁，缪旭弘，唐宇航

（1.哈尔滨工程大学船舶工程学院，哈尔滨150001；2.哈尔滨工程大学烟台研究院，山东烟台264000；3.中国人民解放军92578部队，北京100161）

0 引言

随着人们对振动噪声环境要求的不断提高，船舶振动噪声日益成为船舶设计及广大学者关注的焦点[1-5]。因此，开展船舶结构振动噪声预报方法研究，提高船舶振动噪声定量预报精度，对于提高船舶振动噪声定量设计水平具有重要意义。

在船舶结构振动噪声数值预报方面，汤伟民等[6]基于统计能量法研究了客滚船舱室噪声，提出了基于主要噪声源和传递路径分析的降噪设计策略，但统计能量方法仅能给出频带的分析结果，对线谱捕捉能力显得力不从心；武国启等[7]采用实船试验方法研究了舱室空气噪声激励引起的水下辐射噪声传递特性，给出了舱室空气噪声与水下辐射噪声的关系，该方法虽能实现船舶线谱振动噪声的准确获取，但经济代价高，难以针对整船结构开展线谱振动噪声试验研究；崔杰等[8]采用FEM/BEM 法建立了桨-轴-船尾部结构耦合振动模型，在频域内分析了螺旋桨不同方向轴承力对尾部结构声振特性的影响，实现了桨-轴-船耦合结构振动噪声预报评估，但分析结果对频率步长的依赖性较强；何祚镛等[9]基于声学有限元/边界元法对单双层加肋圆柱壳水下受激振动声辐射进行了研究，详细阐述了声学有限元法/边界元法的具体内容，并开发了基于ANSYS和SYSNOISE软件的计算接口程序。

上述研究多是基于模态叠加理论在频域内进行分析，该类方法具有分析直观等优点，但在进行船舶等大型复杂结构振动噪声分析时求解效率较低，并可能因计算步长选取不当而导致“峰值遗漏”现象，导致计算结果可能出现较大误差。

为此，本研究基于波动理论，提出船舶结构振动噪声时域预报方法，解决船舶结构振动噪声频域预报方法存在的求解效率低下、易出现“峰值遗漏”等难题，旨在为船舶结构振动噪声预报评估提供方法依据。

1 船舶结构振动噪声时域预报方法

1.1 结构动力响应时域分析理论

结构动力时域分析主要应用于结构瞬态动力分析和瞬态声学分析等领域。该方法通过对耦合系统运动方程在时间域内进行数值积分，得到结构在各时段的动力响应，在各时间步长Δt内均可将其视为线性系统分别计算其响应，并依据该时段的结果对结构的各系统参量（位移、应力、压力、声压等）进行修正，并以此作为下一时段系统特性的初值。

对于多自由度系统而言，不论其是线性系统还是非线性系统，其运动方程可以表示为

式中，{P}为激励力矢量，{FI}为惯性力矢量，{FD}为阻尼力矢量，{FS}为结构抵抗变形的力矢量。

假设已知式（1）在每一积分步长初始瞬时t和末了瞬时t+Δt的状态参量，可得

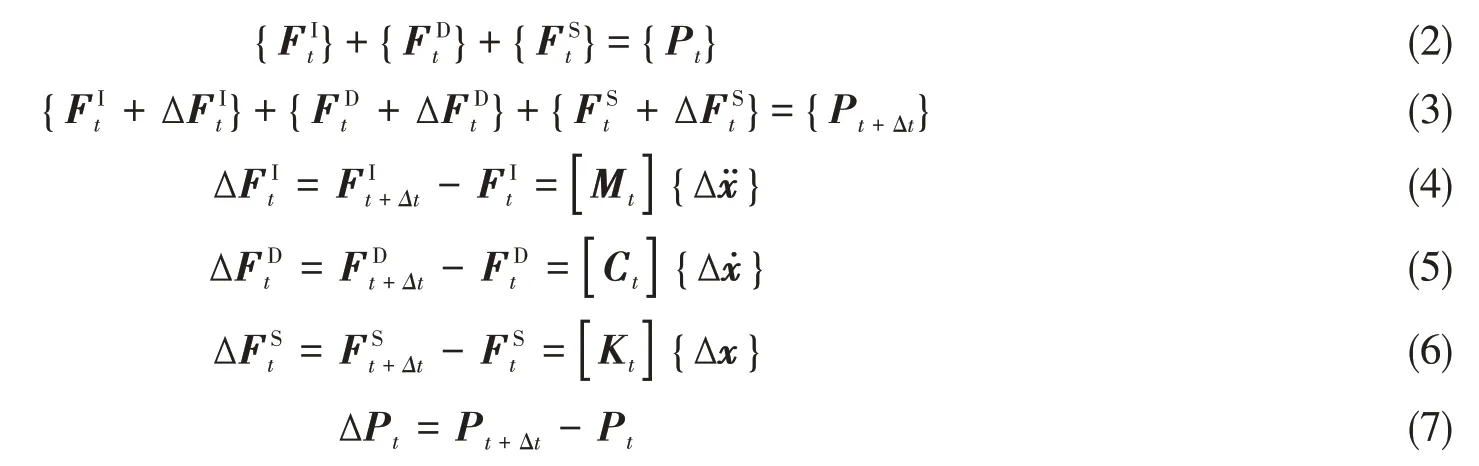
将系统运动在每一积分步长上化为增量形式的方程后有

这里增量方程质量矩阵[Mt]、阻尼矩阵[Ct]及刚度矩阵[Kt]为t时刻的切线斜率，且有

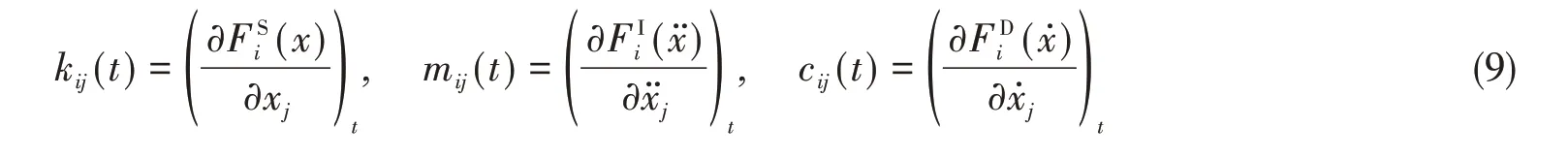
采用矩阵符号来表达，各系数矩阵可表示成

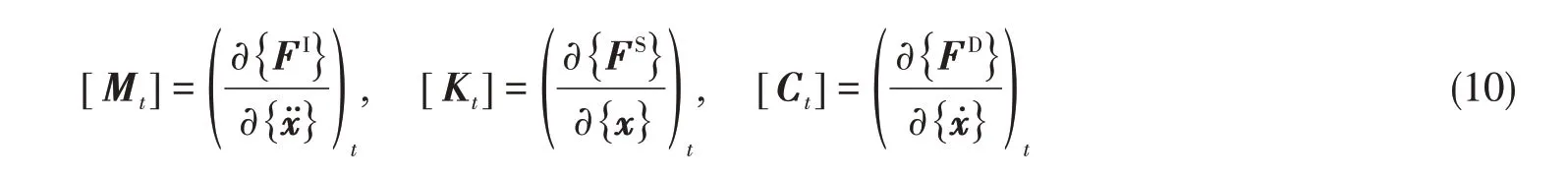
实际动力学问题中，惯性力往往是加速度的线性函数，质量矩阵往往是常系数矩阵，阻尼力常采用等效线性化处理成常系数阻尼矩阵，通常只有刚度矩阵是变化的；如惯性力是加速度的线性函数，非线性力{ }F 依赖于{ }x˙ 和{ }x 时，则系统运动方程为

对应的增量方程为

式中，切线阻尼矩阵[Ct]和切线刚度矩阵[Kt]定义为

其中，切线刚度矩阵定义同式（13），由此得系统在t + Δt瞬时的方程为

式（14）建立了xn和xn+1点加速度、速度和位移的关系。

增量方程的求解可采用有限元法、Newmark-β法和Wilson-θ法等方法进行求解。将位移、速度和加速度改成矢量形式即可得到结构的振动响应，本研究以中心差分法为例作如下说明。

把位移函数按泰勒级数展开（速度、加速度有类似的关系）：

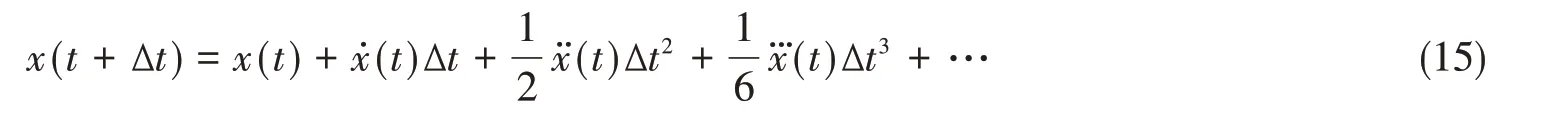
记

由式（16）得前差分公式为

同样得后差分公式为

将式（17）和式（18）相加减，可得用(n - 1,n,n + 1)的位移来近似表示t瞬时的速度和加速度

令t瞬时的位移、速度、加速度满足该瞬时的微分方程

将上述关系式代入后得

由于激励力{P}为瞬态时域信号，而该时域信号理论上可由任意频率组成，故可通过单次分析得到结构的多频响应，从而提高求解效率。但目前时域分析法也存在一定不足：一是时域法进行船舶结构稳态响应分析的收敛速度与预报频率及结构阻尼密切相关；二是时域分析精度易受单元类型及总计算时间的限制，由于结构的时域稳态响应与分析时间密切相关，且显式分析为避免“自锁”现象的发生，多采用低精度单元进行求解，这就使得显式分析的精度易受影响。如能将时域波动分析法引入船舶结构振动噪声预报领域，并对其进行改进，提高其预报精度，有效保障其求解效率，则可实现船舶结构线谱振动噪声的快速预报。

1.2 船舶结构振动噪声时域预报流程

船舶结构振动噪声时域预报方法分析流程可从设备激励载荷的确定、预报模型的建立、边界条件施加和分析结果后处理几个方面进行分析。

（1）设备激励载荷的确定：当已得到基座处设备的时域激励载荷，则时域分析时无需对载荷进行变换；当已得到基座处设备的频域激励载荷，时域分析时需对该频域载荷进行FFT 逆变换，将频域载荷转换为时域载荷。

（2）截断模型的建立：对于船舶结构水下辐射噪声预报而言，由于船舶由大量周期性加筋板架结构构成，如对整船结构进行有限元分析，将耗费大量的人力和物力，并因模型计算规模巨大导致其预报频段及精度大幅下降，严重时可导致计算无法完成。此时如能以局部舱段代替整船模型，对船舶结构振动噪声预报模型进行简化[10]，则可有效提高其预报效率及分析频段，大幅降低计算成本。

（3）边界条件及输出控制：对于船舶结构频段噪声的时域预报而言，由于船舶结构振动噪声的稳态结果依赖计算时间及计算结果的采样频率，故除对预报模型施加相应的边界条件外，还需对模型的计算时间及采样频率进行控制。对于特定频点噪声的频域预报而言，由于其计算结果不依赖计算时间及采样频率，故可按频域法计算要求，制定预报频率，施加相应边界条件，控制输出变量即可。船舶结构振动噪声时域预报流程如图1所示。

图1 结构振动噪声时域预报流程图Fig.1 The process diagram of vibration and noise time domain prediction method

1.3 船舶结构振动噪声时域预报精度及求解效率影响因素分析

（1）采样频率的影响

由采样定理，样本一个周期内至少应包含两个采样点，由此可以确定船舶结构振动噪声时域分析的上限频率f0与系统采样时间间隔ΔT的关系

式（23）可确定分析的频率上限，但还需至少保障1个周期内的样本点数不少于10，由此确定船舶结构振动噪声时域预报的准确频率ft：

（2）时间步长Δt的影响

时间步长Δt是时域分析可查询的最小时间量，其选取直接影响计算结果的收敛性、计算精度及求解效率。通常而言，模型的稳定时间步长δts由声波在结构及流场中的最小波长决定，并由单元最小尺寸确定。计算时间步长Δt与稳定时间步长δts，通常有如下关系：

（a）如时间步长Δt超过稳定时间步长δts，计算结果不收敛；

（b）如时间步长Δt小于稳定时间步长δts，计算结果收敛，可得到较精确的计算结果；

（c）如时间步长Δt 远小于稳定时间步长δts，计算结果收敛，可得到满意结果，但将浪费大量CPU机时，严重降低预报效率。

可见，合理的时间步长Δt应略小于稳定时间步长δts，以同时满足收敛性要求并兼顾求解效率。

（3）计算时间T的影响

船舶结构振动噪声时域预报的精度除与采样频率和计算时间步长等有关外，还与计算时间T 密切相关。如计算时间T 过短，船舶水下声辐射未达到稳态阶段，则其预报精度将受到影响。因此，为保障计算精度，船舶结构振动噪声时域预报的计算时间T应大于船舶结构水下声辐射的稳态时间。

（4）建模因素的影响

不论是时域预报还是频点频域预报，船舶结构振动噪声预报模型的建立对其预报结果往往具有较大影响，如单元类型、网格尺寸及质量和模型尺度等均会对预报结果产生影响，对预报模型进行合理简化，可有效提高船舶结构振动噪声预报的精度及效率。

2 方法有效性验证

2.1 验证模型简介

验证模型为船舶舱段结构，如图2 所示。舱段为总长L=6 000 mm，半径R=1 500 mm 的半圆形结构，壳体厚度t=10 mm，舱段两端设置舱壁，内部设置间距l=600 mm、t1=10 mm、h=200 mm 肋骨；设备尺寸为1 200 mm×600 mm×300 mm（长×宽×高）的方形空心结构，其壁面厚度为t2=20 mm；两隔振器沿船体中心线支撑于设备两端，对称分布于舱段对称中心处，隔振器刚度k=4 kN/m；舱段前后舱壁取简支固定，设备激振力为F = 1× sin(2πft)，垂直作用于设备正中心；流场半径R=6 m，流场外表面敷设无限元，如图3所示。计算频段为20～400 Hz，频率间隔△f=5 Hz，结构损耗因子η=0.05。为便于对比，船舶结构振动噪声时域预报模型与频域预报模型共用同一有限元模型，其中舱段结构单元由4 736个四边形线性单元组成，流场由45 710个六面体单元及3 716个无限元组成，模型共计54 612个单元。

图2 舱段水下辐射噪声预报模型Fig.2 Radiated noise model of a ship cabin

图3 舱段结构水下噪声预报模型边界条件示意Fig.3 Boundary conditions of calculating model

为便于对比分析，计算中分别在舱段结构与流场设置了振动及声压考核点，振动考核点沿舱段结构对称轴线布置于舱段肋骨处，流场声压考核点设置于舱段与流场交界面及半径R=6 m 流场正下方对称中心处，流场声压考核点设置如图4所示。

图4 舱段结构振动及流场声压考核点布置Fig.4 Vibration and sound pressure observation points of ship cabin

由于时域预报需将频域载荷转换为时域信号，为此，本研究采用式（25）对频域载荷进行时频转换。

考虑到预报频段为中低频（≤400 Hz），时域载荷时间间隔ΔT=10-4s；考虑到舱段进入稳态水下声辐射所需时间的影响，时域载荷作用时间取Tt=1.5 s。时域载荷曲线如图5所示。

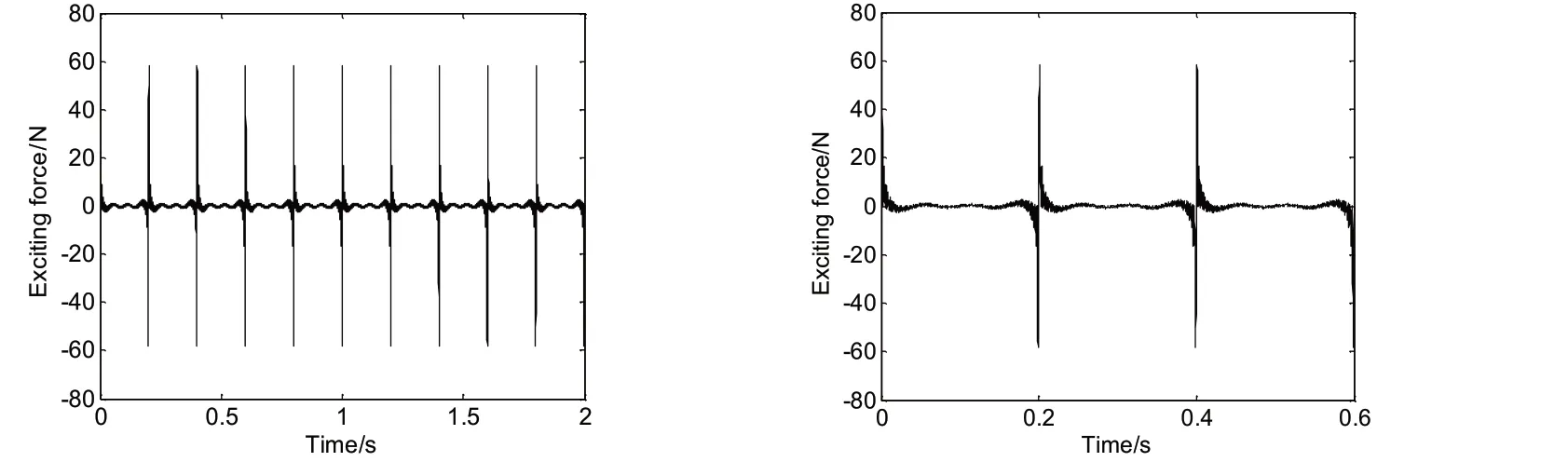
图5 船舶结构噪声预报时域激励载荷曲线Fig.5 Load curve in time domain of ship structural borne noise prediction model

输出控制方面，为保障计算结果的有效性，对振动及声压考核点的采样时间间隔设置为ΔT=10-4s。

2.2 计算结果分析

2.2.1 方法有效性分析

本研究分别采用时域分析方法及频域分析方法开展了船舶舱段结构的振动噪声预报，并将两种方法的预报结果进行了对比。图6给出了舱段振动噪声预报模型典型考核部位振动及声辐射时历曲线；图7 给出了舱段结构典型时刻水下声辐射分布；图8 给出了舱段振动噪声预报模型典型考核部位振动及声辐射时域分析结果与频域分析结果对比曲线，图中时域分析结果为t≥1 s后船舶舱段结构稳定段响应的FFT变换结果，频域分析结果为采用频域分析方法所得的船舶舱段结构稳态响应结果。

图7 载荷激励下舱段结构典型时刻水下声场分布图Fig.7 Underwater sound radiation of ship cabin at typical time

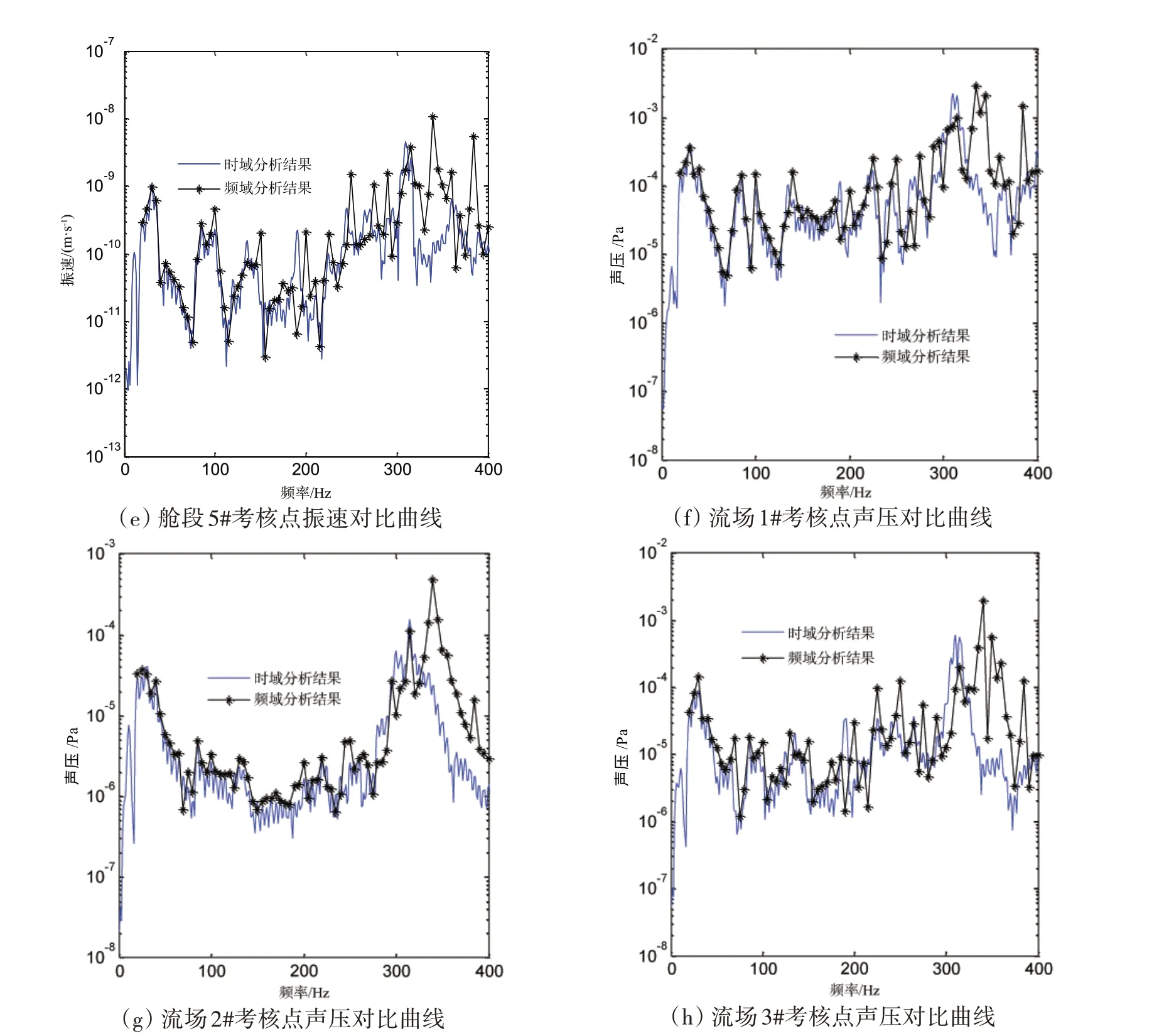
图8 舱段模型典型考核部位振动及声辐射时频对比曲线Fig.8 Vibration and sound radiation curve at typical observation points of ship cabin

由图6 可以看出，当计算时间t≥0.4 s 时，船舶舱段结构振动及声辐射即进入稳态振动阶段，船舶舱段结构水下声辐射也进入稳态声辐射。由此可以看出，采用时域预报方法可以得到结构的稳态振动响应。

图7清晰给出了船舶舱段结构水下稳态振动声辐射情况，可以看出，不同时刻船舶舱段结构的水下声辐射各不相同，通过典型时刻船舶舱段结构水下振动声辐射分布可以直观得到船舶结构激励载荷下的真实水下声辐射，由此可通过时域分析方法真实模拟船舶结构的水下振动声辐射。

对比图8中典型考核点时域分析与频域分析结果可以看出，一方面，时域分析与频域分析结果在低频段吻合良好，两种方法所得结果基本一致，但随着频率的提高，两方法所得结果的差异在逐渐增大，特别是在300～350 Hz 频段附近，时域分析结果与频域分析结果存在一定差异，主要表现为时域分析结果的峰值较频域分析结果的峰值更为突出，并存在一定的频率左移现象（频域分析结果峰值频率较时域峰值频率落后约20～40 Hz），但总体而言，时域分析结果与频域分析结果是基本吻合的。另一方面，对比同一考核部位时域分析结果与频域分析结果曲线可以看出，时域分析结果的频率成份较频域分析更为丰富，这说明时域分析更易激起结构的振动模态。由此可见，采用时域方法进行船舶结构振动噪声预报是可行的。

2.2.2 方法求解效率分析

现在分析船舶结构振动噪声时域预报方法的求解效率，对于本研究的船舶舱段结构振动噪声预报而言，在同一计算硬件配置时，采用时域预报及频域预报方法所需的资源如表1所示。

表1 船舶结构噪声时域预报与频域预报求解时间对比Tab.1 Comparison of solution time between time domain and frequency domain prediction method of ship structural borne noise

由表1可以看出，不论是从内存使用，还是在CPU 求解时间方面，时域方法均优于频域预报方法。特别是对于实船结构而言，由于其计算规模远大于本算例模型，在普通计算机上采用频域预报将存在较大困难，而采用时域预报方法则可以方便、快速得到实船的水下声辐射；另一方面，由于时域预报方法的计算规模与其网格数量大致呈线性增长，其对内存的要求也较低，故其分析频率可以更高。

综上分析可知，采用时域预报方法开展船舶结构振动噪声预报可以保障预报的效率，真实反映船舶结构的振动和水下声辐射，避免漏峰现象的发生。由此可见，本研究提出的船舶结构振动噪声时域预报方法是可行的，其有利于保障船舶结构振动噪声预报的求解效率与精度，及时发现船舶结构振动噪声设计的关键点，为船舶结构振动噪声快速治理提供方法支撑。